雾霾污染与城市规模的非线性关系——基于我国城市数据的分析

孔 晗，刘 帅

(1.武汉大学 区域与城乡发展研究院，湖北 武汉 430072;2.北京大学 中国农业政策研究中心，北京 100871)

一、问题与文献

(一)问题的提出

我国城镇化率不断提高，从2007年的44.9%提高到2017年的58.52%，随之而来的是城市规模的不断扩大，城区人口在100万以上的城市从2007年的57个增加到2016年的75个；特大城市人口不断增加，北京、上海城区人口分别已达1879万和2419万。城市规模的持续扩大带来了“城市病”，其中污染已成为“城市病”之首，严重困扰人的健康。研究表明，空气污染造成人均缩短寿命5年，健康损失价值超过200亿元。城市污染日益引起社会关注和高层重视，十九大报告明确指出：坚决打好污染防治攻坚战。当前，我国环境污染形势依旧严峻，2016年全国338个地级以上城市中，仅有84个环境空气质量达标，占总数的24.9%，254个城市环境空气质量超标(轻度污染以上)，占75.1%。

城市污染与城市规模具有紧密联系。随着城市规模不断扩大，城市污染排放总量也不断增大。城市规模的扩大给生态环境带来巨大压力，为此，多地对城市规模做出了明确限制，如北京从生态承载力角度出发，确定人口规模控制并长期稳定在2300万以内。控制城市规模似乎已成为各地治理“城市病”的重要手段。但从另一角度讲，城市规模扩大有利于规模经济的形成，人口高度集聚将带来高效减排，城市污染将出现边际递减的现象，从而导致人均污染逐渐下降。空气污染已成为影响居民生命健康的最主要因素，且空气污染具有易观性、民众可见度高，更能引起治理关注。已有研究表明，对可见度高的污染(如大气污染)治理效果明显高于可见度低的污染(如水污染)[1]。本文重点关注空气污染与城市规模的关系。

实施新型城镇化，加快农业转移人口市民化势必会引起城市规模的进一步扩大。那么，城市规模的扩大必然导致污染加剧吗？城市污染与城市规模之间存在怎样的关系？控制城市规模能够改善城市环境状况吗？本文基于我国城市层面的面板数据，考察两者之间的关系。

与现有研究相比，本文的创新点在于：一是构造了全国278个地级及以上城市十年的非平衡面板数据，时间跨度长且观察样本大。二是利用拓展的STIRPAT模型考察了城市污染与城市规模之间的非线性关系，并在一系列验证后得到了一致性结论。三是建立了静态和动态面板模型，使用双向固定效应和系统GMM估计，尽可能缓解了内生性问题，使结论更加稳健可靠。

(二)文献综述

城市污染与城市规模的关系，已引起部分学者关注。文雯、王奇认为，污染与城市规模存在“倒U型”关系[2]。郑怡林、陆铭则认为，人口规模与污染指标没有相关性[3]。马素琳等认为，人口规模是影响城市空气质量的主要因素，且影响程度因城市规模大小表现出异质性[4]。对此，国外学者有不同看法。Oliveira等发现，随着城市规模的扩大，二氧化碳的排放量也不断增大[5]。Shukla and Parikh研究了空气质量和城市规模之间的关系，发现两者之间具有显著关系，且这种关系在发达国家和发展中国家具有差异性[6]。

梳理已有研究可知，对于城市污染与城市规模之间关系的研究较少且还存在以下不足：第一，使用的数据，以省级数据和截面数据居多。即使少数学者使用了城市层面的数据，也缺乏对数据的有效处理和筛选。第二，存在遗漏变量、内生性等问题。本文利用PM2.5数据构造了全国278个地级及以上城市2007-2016年十年的面板数据，使用双向固定效应模型、系统GMM估计方法，力图克服上述不足，得到更加稳健的结论。

二、计量模型与数据来源

(一)理论分析与研究假设

城市规模对雾霾的影响有两种效应：污染总量扩大和规模集聚减排。随着城市规模不断扩大，一方面，各类经济活动不断增加，非农产业不断扩大，而经济发展所需的能源仍以化石能源为主，清洁能源利用率低；在北方地区，冬季取暖对雾霾具有明显的扩散效应，而供暖面积随城市规模的扩大也不断上升。已有研究表明，我国城市供热面积在1991-2013年间增加了20倍[7]。生活水平的提高使得汽车消费总量也不断增加；在人类活动中，交通是城市污染的最大来源[8][9]。同时，城市规模扩大导致城市拥堵，而交通拥堵会明显加剧雾霾[10][11]。另一方面，当城市达到一定规模，集聚效应和规模效应开始显现，能源的集中利用有利于提高能源使用效率，集中供热也明显有利于空气质量改善[12]，空间集聚也能够降低工业排放强度[13]。由于城市规模的集聚效应，使得污染排放的增速低于城市规模的扩张速度，从而使得两者表现出负向关系。

为了更加直观地观察两者之间的关系，我们绘制了雾霾与城市规模的相关关系图(见图1)。纵轴表示PM2.5浓度，横轴表示城市规模。图中同时给出了PM2.5浓度与城市规模之间线性和二次非线性的OLS回归方程和拟合曲线。其中，实线是线性拟合曲线，从散点图的分布来看，两者之间的线性关系并不明显；虚线是二次拟合曲线。从回归方程的R2可以看出，非线性曲线对两者之间的关系解释度更大。

基于以上分析，提出以下假设：即雾霾与城市规模之间存在非线性关系。

图1 雾霾与城市规模相关关系

(二)计量模型

Ehrlich and Holdren提出的IPAT模型，是分析人类活动对环境影响的经典模型[14]。该模型的基本方程为I=PAT,其中I表示污染，P表示人口，A表示富足水平(可理解为人均消费或人均GDP)，T表示技术(可以理解为单位经济活动对污染的影响，可以扩展为多个经济变量)。IPAT模型很快得到了认可，并被不断扩展为ImPACT、IPBAT、ImPACTS等[15]，这一系列简明模型在最初提出时对于分析污染的影响因素得到了广泛应用[16][17]。然而，这类模型具有明显不足：第一，它认为污染的变动和各影响因素的变动是同比例的，即P(或者A、T)增加一倍，环境污染也增加一倍，这与事实明显不符。第二，模型是以恒等式的形式给出的，无法进行假设检验。第三，无法进行非线性关系识别[18]。为了克服IPAT模型的缺陷，Dietz and Rosa将此模型发展为STIRPAT随机模型[19]：Ii=aPbiAciTdie

(1)

取对数：lnIi=a+blnPi+clnAi+dlnTi+ei.

(2)

a是常数项，b,c,d均为系数，e为误差项。Dietz and Rosa同时指出，P、A、T可以分解，把一些其他合理的控制变量加入其中。STIRPAT模型已得到广泛而成功的运用，本文基于STIRPAT模型，借鉴已有文献，建立城市雾霾与城市规模的计量模型:

lnPMit=α0+α1lnPopit+α2lnPGDPit+

α3lnTit+μi+λt+ηit

(3)

对于城市污染，本文重点关注空气污染。雾霾是空气污染的主要形式，故选择PM2.5的城市面板数据作为雾霾的衡量指标。城市规模用城市人口来衡量。式中，Pop表示城市人口，为核心解释变量；PGDP为人均GDP，用以表征经济发展水平；T表示其他影响因素；μi为城市固定效应，λt为时间固定效应，ηit为随机扰动项。

为探讨雾霾与城市规模之间的非线性关系，在模型(3)右边增加城市人口的平方项和三次方项，探索可能存在的多种非线性关系。环境库兹涅茨曲线认为，污染与经济发展水平存在倒“U”型关系，所以在模型中还加入经济发展的平方项。还有其他影响城市雾霾的变量，笔者试图将T分解为以下变量：外商投资(FDI)，为影响城市污染的重要因素[20]，用当年利用外资金额来衡量；城市财政状况(Rev)，也对城市污染具有重要影响[21]，它可以衡量该城市治理污染的财力情况，用各城市财政收入表征。此外，考虑到城市层面的异质性和其他可能影响到城市环境的因素，尽可能减少遗漏变量，还加入了产业结构、能源消费、绿地面积、道路面积、工业企业个数等控制变量。对于产业结构，使用第二产业占比(Ind)表示；能源消费用供气总量(Gas)、液化石油气供应量(LPG)表示；绿地面积(Green)、道路面积(Road)、工业企业数(Ent)分别使用相应城市的该数据表示。这样，基础回归模型变为：

lnPMit=α0+α1lnPopit+α2(lnPopit)2+α3(lnPopit)3+α4lnPGDPit+α5(lnPGDPit)2+α6lnFDIit+α7lnRevit+βX+μi+λt+ηit

(4)

模型(4)虽然控制了一系列控制变量，但仍存在内生性问题：一是不可观测因素随时间变化引起的内生性；二是解释变量与被解释变量存在联立内生性。为了克服内生性问题，同时考虑到雾霾具有时间依赖性，即上一期污染水平对当期有影响，引入雾霾的滞后项作为解释变量，构造动态面板模型：

lnPMit=α0+γlnPMit-1+α1lnPopit+α2(lnPopit)2+α3(lnPopit)3+α4lnPGDPit+α5(lnPGDPit)2+α6lnFDIit+α7lnRevit+βX+μi+λt+ηit

(5)

模型(4)用双向固定效应模型进行估计，即同时控制地区固定效应和时间固定效应，采用聚类稳健标准误差。模型(5)动态面板可分为长面板和短面板。截面维度n较小而时间维度T较大的长面板，由于其本偏差较小，采用最小二次虚拟变量法(LSDV)进行估计。而本文使用短面板，一般采用差分GMM方法和系统GMM方法。差分GMM容易出现弱工具变量问题，且系统GMM将水平方程和差分方程作为一个方程系统进行估计，更具有效率，所以使用系统GMM方法估计动态面板模型。系统GMM估计，通常需要进行工具变量的有效性检验，常见方法是Sargan检验和Hansen J检验。Arellano等指出，Sargan检验统计量P值都不是很大[22]；另外，Sargan检验在稳健标准误差下无法检验，所以选择Hansen J检验工具变量的有效性。Hansen J检验的原假设是：所有工具变量均有效。这里用AR(1)和AR(2)检验残差的一阶和二阶序列相关性；GMM估计要求残差二阶序列不相关。

回归过程借鉴Wu et al.的做法[23]，先对模型进行整体回归，若城市规模的三次项不能通过10%水平显著，则删除三次项，然后对模型再回归；若城市规模的二次项不能通过10%水平显著，则删除二次项后对模型进行再回归。根据系数的显著性和方向，可以判断雾霾与城市规模的关系，具体方法如表1所示。

表1 系数与曲线关系判断

(三)数据来源与说明

被解释变量为PM2.5，该数据来自哥伦比亚大学社会经济数据与应用中心，该中心运用卫星搭载设备通过气溶胶光学深度(AOD)反演和GEOS-Chem化学传输模型计算得到PM2.5数据，并根据全球地基观测值使用地理加权回归(GWR)进行校准。使用该数据既弥补了我国早期相关数据的不足，同时又具有客观性。

核心解释变量为城市规模，通常使用城市人口来衡量。由于人口流动愈加频繁，用户籍人口不能准确衡量城市规模，而城市常住人口又包括农村人口。本文用常住人口乘以城镇户籍人口占总人口比例来衡量城市人口。对于个别省份，如黑龙江、吉林等，未公布常住人口的省份，就尽可能通过城市的《统计年鉴》进行补充，实在难以搜集到数据的，就用城镇户籍人口替代。

本文其他变量原始数据主要来自历年《中国城市统计年鉴》，笔者对原始数据进行了一系列处理。人均GDP数据，处理成以2007年为基期的可比数据。当年使用外资金额，先用当年的人民币汇率年平均均价换算为人民币，再用GDP平减指数进行平减。其他涉及到价格因素的变量，也照此处理。

首先剔除了缺失值，然后把值为0的数据赋值为1，使其取对数时有意义。最后得到278个地级及以上城市2007-2016年十年的非平衡面板数据，表2为主要变量的描述统计。

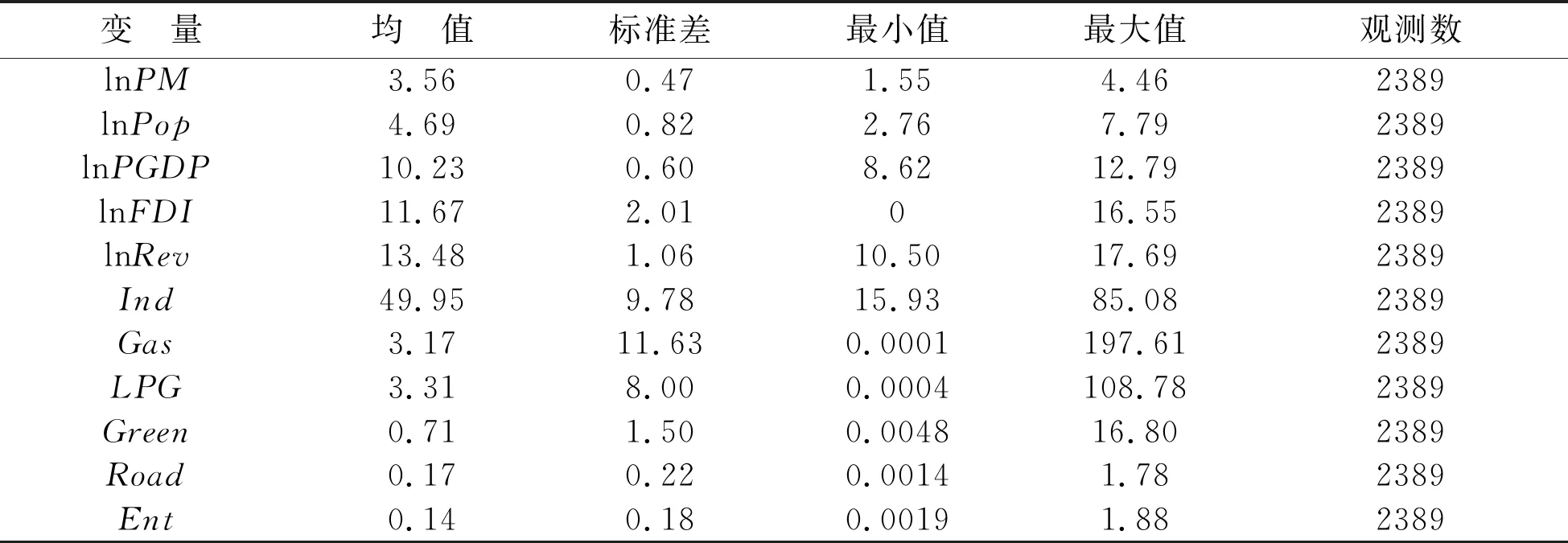
表2 变量描述性统计

三、回归结果与分析

(一)雾霾与城市规模的关系

首先用全样本对模型(4)、(5)进行回归，使用双向固定效应对模型(4)进行估计。对于模型(5)，把控制变量以外的所有解释变量视为内生变量，使用系统GMM方法估计。结果如表3第(1)(2)列所示。从列(1)的结果看，核心解释变量城市规模的一次项显著为负，二次项显著为正，三次项显著为负，表明雾霾与城市规模呈现倒“N”型关系。列(2)为动态面板的系统GMM估计结果，核心解释变量的显著性和方向与列(1)一致，且都至少在10%水平下显著；雾霾的滞后一期显著为正，说明具有一定的时间依赖。从列(2)的相关检验可以看出，Hansen J 检验不拒绝“所有工具变量均有效”的原假设，表明工具变量有效。但AR(2)却表明残差二阶序列相关，影响系统GMM估计的一致性。

陈强认为，工具变量有效，但残差二阶序列却相关，很可能是因为扰动项自相关导致的，在模型中进一步加入解释变量的二阶滞后性能够缓解该问题[24]。由此模型(5)变为：

lnPMit=α0+γ1lnPMit-1+γ2lnPMit-2+α1lnPopit+α2(lnPopit)2+α3(lnPop)3+α4lnPGDPit+α54(lnPGDPit)2+α6lnFDIit+α7lnRevit+βX+μi+λt+ηit(6)

仍采用系统GMM对模型(6)进行估计，结果如表3第(3)列所示。结果表明，核心解释变量lnPop、(lnPop)2、(lnPop)3均与前述回归一致，表明雾霾与城市规模之间的倒“N”型关系比较稳健。从滞后项看，滞后两期和滞后一期都是显著的正向影响，说明雾霾的时间依赖性强，具有较强的滞后性。从相关检验看，Hansen J仍表明工具变量的有效性；AR(2)检验不拒绝原假设，说明列(3)残差二阶序列相关确实是由扰动项自相关导致的。

通过比较，得出以下结论：城市雾霾与城市规模之间呈倒“N”型关系，在双向固定效应与系统GMM估计下均显著，说明这种关系具有一定的一致性和稳健性；雾霾具有时间路径依赖，具有较强的持续性。进一步分析得知，规模较小城市雾霾与城市规模之间存在负向关系，这可能因为城市在发展初期，规模增长较快，大于雾霾排放的增长速度；城市规模达到第一个拐点后，两者之间呈现出正向关系，即随着城市规模的不断扩大，城市雾霾也不断加重；大城市的规模效应已经形成，城市雾霾与城市规模又呈现负向关系。

表3 回归结果

进一步分析其他变量对城市雾霾的影响。回归结果显示，雾霾与经济发展之间并没有呈现倒“U”型库兹涅茨曲线；事实上，中国是否存在“环境库兹涅茨曲线”也饱受争议，王敏、黄滢发现，中国环境库兹涅茨曲线呈“U”型[25]，跟笔者的回归结果一致。外商投资则加剧了雾霾，印证了“污染天堂”假说，提醒在引进外资时要注意提高准入门槛，防止发达国家污染转移。城市财政状况对雾霾的影响偏负向，但不够稳健，说明财政在雾霾治理中并没有发挥积极作用。控制变量中，产业结构、城市绿地面积、工业企业数对城市污染的影响非常微弱。

(二)不同地区雾霾与城市规模的关系

我国幅员辽阔，各地区之间城市发展水平存在较大差异，以下分不同地区(东部、中部、西部)考察雾霾与城市规模的关系。用各地区的子样本对模型(4)和(6)进行估计，结果如表4所示。

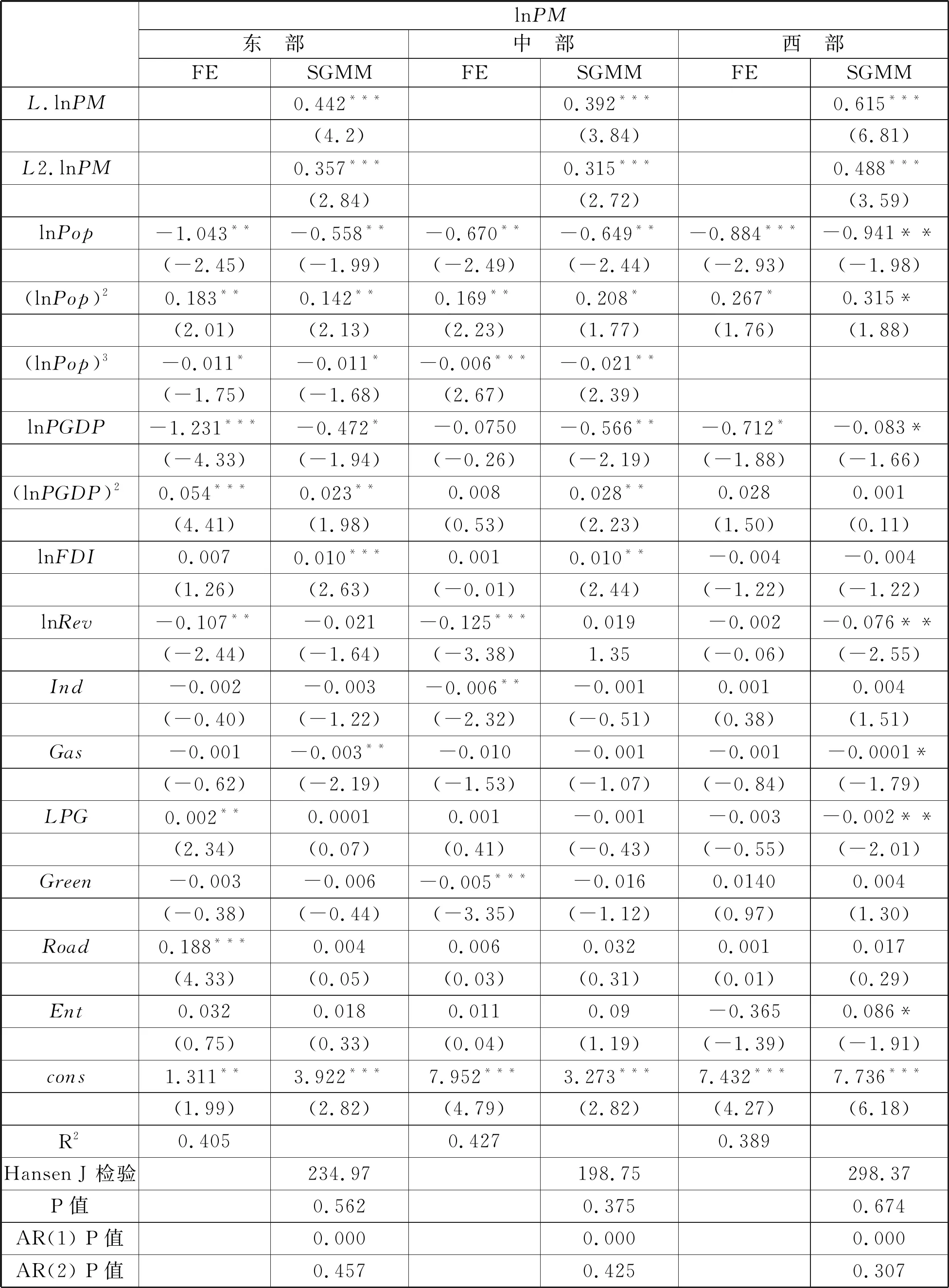
表4 分地区回归结果

结果显示，东、中、西部之间也存在明显差异。东部和中部地区雾霾与城市规模仍呈现显著的倒“N”型关系；而西部地区的三次项不显著，进而考察二次项，发现西部地区的一次项显著为负，二次项显著为正，表明雾霾与城市规模之间呈现“U”型关系。分地区系统GMM估计的Hansen J 检验和AR(2)检验表明，选取的工具变量均有效且残差二阶序列无关，再次证明本文较好地解决了内生性问题。从滞后项系数和显著性看，雾霾的时间依赖性在三个地区都非常显著。分地区回归结果差异性可能归因于城市发展阶段的不同。西部地区城市发展落后于东部和中部地区，正处在倒“N”型关系的前段，处在城市规模的初步扩张阶段，所以呈现出“U”型关系。

四、进一步讨论：不同级别城市的差异

已有研究表明，城市行政级别优势对其规模的扩张有明显的促进作用[26]，行政级别越高，规模扩张也越快[27]。前文研究已表明,城市规模对雾霾具有显著影响，那这种影响是否因城市行政级别不同而存在差异呢？进一步将样本按城市行政级别分为副省级以上城市和普通地级市，分组进行回归分析。通常将广州、武汉、哈尔滨、沈阳、成都、南京、西安、长春、济南、杭州等省会城市和深圳、大连、青岛、厦门、宁波5个计划单列市作为副省级城市，本文将副省级城市外延扩大，界定为主要领导是副省级的城市，包括所有省会城市和部分地级强市。将按城市行政级别分组的样本按模型(4)和(6)进行回归，结果如表5所示。

在副省级城市中，城市规模的三次项并不显著，进一步考察二次项，发现在副省级城市中，雾霾与城市规模呈现倒“U”型关系。普通地级市中，两者之间倒“N”型关系在10%显著水平下通过检验。回归结果表明，无论是副省级以上城市还是普通地级市，雾霾的滞后两阶都非常显著，表明污染的时间持续性在城市行政级别上没有显著差异。两组的系统GMM回归的Hansen J 检验和AR检验再次表明，工具变量有效一致。

副省级城市与普通地级市之间的差异可能是由城市发展的不同阶段造成的。副省级城市一般是当地的中心城市，对周边人口、资源的吸附能力强，人口较为集中，普遍已经跨过了初级发展阶段，即跨过了倒“N”型的第一个拐点，处在后半段，所以在副省级城市中,雾霾与城市规模呈现倒“U”型。

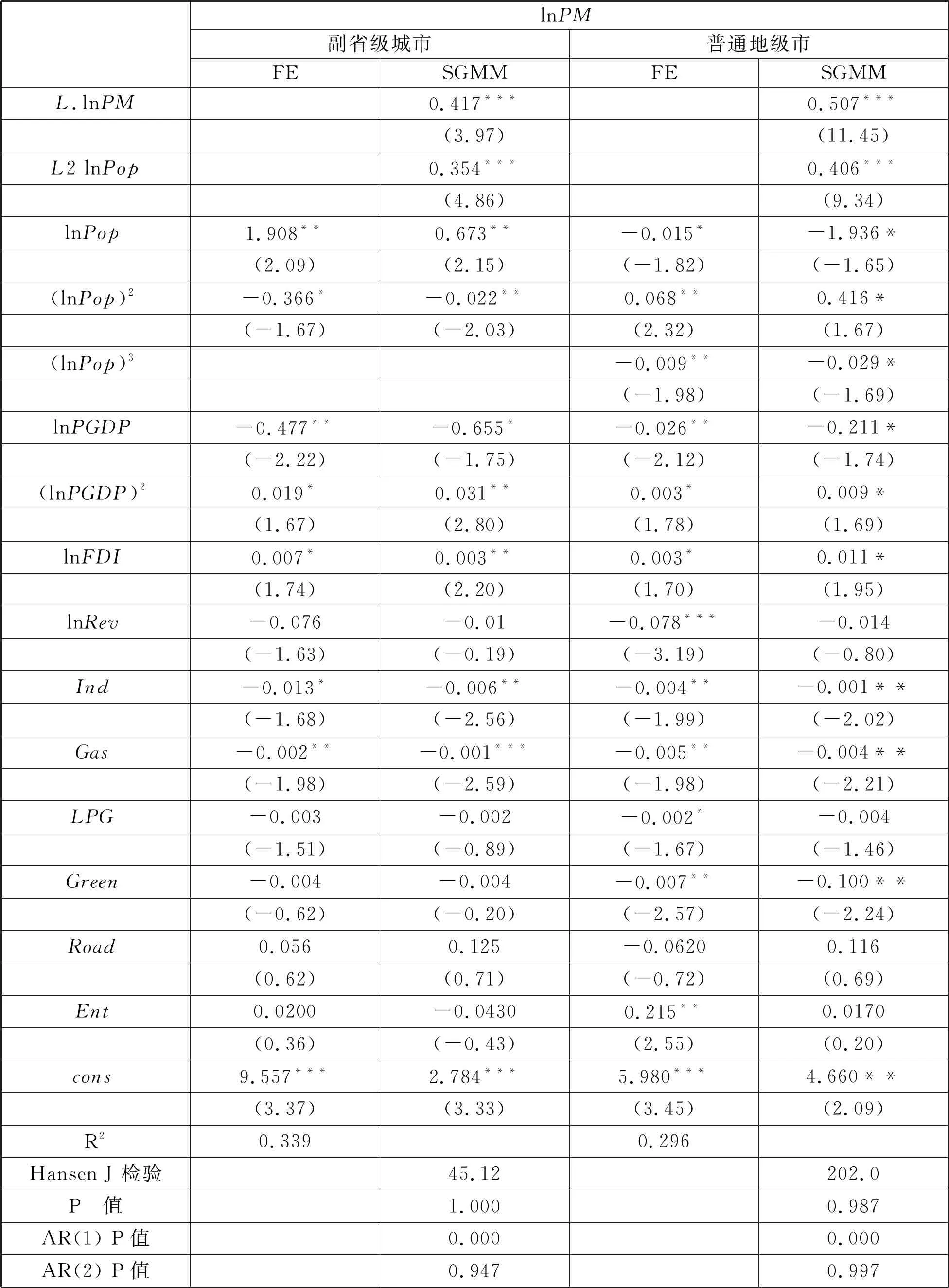
表5 按城市级别分组的回归结果

五、结论与启示

综上分析，得出以下主要结论：一是城市雾霾与城市规模存在倒“N”型关系，即在城市发展初期，雾霾与城市规模呈负向关系，当跨过第一个拐点后，雾霾随城市规模的扩大而加重，直到城市规模达到第二个拐点时，两者又呈现负向关系。二是这种关系具有明显的地区差异，在东部和中部，雾霾与城市规模仍呈现显著的倒“N”型关系，而西部地区则呈现“U”型关系。这是由城市发展阶段不同造成的，即东、中、西部城市处于不同发展阶段。三是雾霾存在显著的时间路径依赖，持续性在滞后两期仍非常明显。经济发展水平、能源消费、外商投资等其他因素对城市雾霾也具有一定影响。四是雾霾与城市规模之间关系由于城市级别不同表现出了一定差异，倒“N”型关系在普通地级市中更为显著。

以上结论的政策内涵是：首先，认识雾霾与城市规模之间的倒“N”型关系对于制定城市发展规划具有重要参考意义。我国目前规模在100万人以下的城市，即中等规模城市，发展水平还较低，但随着城市化不断推进，这些城市很快就会跨过第一个拐点，环境和人口即将面临双重压力。处在这个发展阶段的城市应“未雨绸缪”，做好环境控制预案，走环境与经济协调发展道路。城市规模在100万～1000万的大城市，处在环境随城市规模扩大而不断恶化的阶段，必须加大环境治理力度，打赢环境治理攻坚战，建立生态宜居城市。超大城市，如北京、上海等，已达到环境的规模经济阶段，政策着力点应转向优化人口结构。其次，治理雾霾要持之以恒、坚持不懈，综合考虑多方面因素，将其作为一个系统工程持续推进。雾霾具有很强的持续性和时间依赖性，必须常抓不懈，防止治理半途而废，进而造成污染反弹。正确处理经济发展与环境污染之间的矛盾，走可持续发展之路；优化能源消费结构，推广使用清洁能源；制定合理的外资准入标准，防止境外污染转移。最后，无论是地区差异还是级别的差异，都表明雾霾具有一定的地区性特征，要考虑各地的经济发展水平、区域位置、城市级别等因素，因城施策，赋予地方更多的治污自主权。