基于数字岩心的碳酸盐岩孔隙结构对弹性性质的影响研究(上篇)：图像处理与弹性模拟

赵建国， 潘建国， 胡洋铭， 李劲松， 闫博鸿， 李闯， 孙朗秋， 刘欣泽

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 中国石油勘探开发研究院西北分院， 兰州 730020 3 中国石油勘探开发研究院， 北京 102258

0 引言

碳酸盐岩储层囊括了全球60%的石油储量，且开采潜力巨大.相较于常规砂岩储层，碳酸盐岩储层的特点是后期的成岩改造作用会导致其次生孔隙非常发育，使其孔隙结构极其复杂(Bathurst, 1971; Lucia, 1983).碳酸盐岩中常见的孔隙结构类型有铸模孔、粒内溶孔、粒间溶孔、晶间孔、裂缝等，这些复杂多变的孔隙结构会对碳酸盐岩的弹性性质产生显著的影响，甚至超过孔隙度的影响(Anselmetti and Eberli,1993,1999).比如Zhang等(2015)提到，孔隙度13%的四川碳酸盐岩储层的纵波速度会因孔隙结构不同而有约1 km·s-1的速度差异.如果不能很好地考虑孔隙结构因素，碳酸盐岩储层反演误差将会非常大.因此，孔隙结构特征的研究对碳酸盐岩的储层反演、含油性评价具有重大意义.

在缺乏对岩石几何结构性质的准确描述下，以往学者对岩石的弹性性质预测往往局限于等效介质理论和经验公式.经典的等效介质理论有Hashin和Shtrikman等(1962)提出的上下边界法、Kuster和Toksoz等(1974)提出的K-T模型、Budiansky和O′Connell(1976)提出的自相容近似(self-consistent approximations of effective moduli，SCA)模型和Berryman(1992)提出的微分等效介质模型(differential effective medium model，DEM).上下边界法由于固体介质与孔隙流体弹性模量差异过大，因此只能给出混合物大致的上下限.K-T、SCA、DEM等这些模型均只考虑岩石含有球体状、针状、盘状、以及硬币状缝隙孔等具有理想化形态的孔隙结构.而碳酸盐岩孔隙类型非常复杂，这样理想化的孔隙结构显然无法代表实际的孔隙特征.经验公式主要有Wyllie等(1956)提出的时间平均方程、Han等(1986)提出的含泥砂岩经验公式和Raymer等(1980)提出的Raymer-Hunt-Gardner经验关系式.经验关系本质上是对某一区块大量岩石数据的统计结果与总结形式，缺乏与孔隙结构间的联系.对于含复杂孔隙结构的岩石，其效果往往不好.综上，这些经典的岩石物理模型对于碳酸盐岩常常不适用.

如果所建立的岩石模型能考虑岩石中真实的孔隙结构，就可以极大地提高弹性预测的准确性.幸运的是，高分辨率微米CT成像技术能准确刻画岩石内部固体颗粒与孔隙的复杂几何形状，建立更真实的岩石模型，在此基础上进行弹性预测将更加准确.这项技术被称为数字岩石物理(digital rock physics，DRP)，其主要由三个步骤组成：(1)岩石CT扫描;(2)图像处理以建立数字岩心模型;(3)岩石的弹性数值模拟.DRP技术率先在均质性好的砂岩取得了成功，并用实验测量结果得到了很好的验证.Liu等(2017)针对砂岩样品考虑识别多种矿物组分从而进行了高精度的建模，此外孙建孟等(2012)在数字岩心建模和弹性、电性、渗流等多种岩石物理性质的模拟与应用上对DRP技术进行了归纳，这些学者在数字岩心领域做出了突出贡献.而对于碳酸盐岩，由于其复杂性与非均质性仍是一项挑战，很少有学者模拟具有强非均质碳酸盐岩的弹性性质.

图像处理的主要目标是对经过CT扫描所建立的三维数字岩心数据体进行有效的处理，高精度地分离孔隙与岩石骨架，从而建立与实际岩石样品相符合的数字岩心模型，以满足后期利用三维数字岩心模型进行电性质、弹性性质、核磁性质以及渗流性质等数值模拟的需求.要建立准确的数字岩心模型需要对原始CT数据进行图像处理，常用的图像处理手段主要有空间滤波、去噪、去伪像、阈值分析、形态学运算和聚类分析.对于图像处理，Sheppard等(2004)提出图像增强与分割的三步法，能达到去噪、边缘增强、图像保真与较好分割的效果.Iassonov等(2009)验证了多种阈值和局部自适应分割技术在CT扫描图像中的应用效果，并得出利用局部图像信息如空间相关性以及应用局部自适应技术能得到较好的处理效果的结论.赵秀才等(2009)在Otsu分割方法的基础上提出实测孔隙度约束分割效果的改进Otsu法，并使用均质纯净砂岩进行了方法验证.Tuller等(2013)回顾了全局和局部自适应两相以及更复杂的多相算法，提出基于马尔科夫链随机场算法的多相分割法能达到自动分割且质量良好的效果.张磊等(2015)从分形理论的角度分析岩石孔隙结构的分形信息来改进Otsu算法.但以上学者所提出的图像处理方法通常只适用于像纯净砂岩这类组成成分比较简单的岩石，主要原因在于构成该类岩石的岩石颗粒均匀，分选较好，岩石的孔隙结构相对简单均匀，因此该类岩石的数字岩心图像处理相对简单，特别是如上提及的二值化分割技术具有良好的适应性.而对于具有复杂孔隙结构(缝、洞、缝-洞组合型结构等)的碳酸盐岩的数字岩心模型，这些方法的适用性需要仔细研究，以期能够建立反映真实碳酸盐岩孔隙结构的去噪滤波等图像处理、与进行骨架与孔隙分割的二值化处理流程.

对于数字岩心的弹性性质，Garboczi和Day(1995)提出利用有限元法模拟三维数字岩心所代表岩石的弹性模量，该方法将弹性位移分布的物理问题转化为利用最小位能原理求解的数学问题并使用有限元法进行求解.Arns等(2002)在Garboczi和Day(1995)的工作基础上，提出使用快速共轭梯度法来对有限元方程进行迭代收敛以逼近系统最小能量，最后求得数值解即为6个方向的应力与6个方向的应变进而求得等效模量.Makarynska等(2008)采用上述提到的线弹性有限元法模拟部分饱和岩石的弹性参数并与Gassmann理论和Wood公式(GW)结合公式进行比较，发现部分饱和流体模拟结果比较精确，非常适用于单矿物宏观均匀多孔介质.然而，Garboczi(Garboczi and Day, 1995; Garboczi and Berryman, 2001)基于有限元进行弹性性质数值模拟的详细理论推导并没有见诸于相关文献，以及对该算法进一步优化与效率升级等方面未见有相关改进的报道.

本论文作为两篇系列文章的第一篇(上篇)，主要解决的问题有二：一是提出了一套适用于碳酸盐岩的图像处理流程，并通过孔隙度标定来验证所建立的数字岩心模型的准确性和图像处理流程的有效性，在此基础上，建立的三维数字岩心数据体用来进一步进行弹性性质模拟；二是为了方便读者深刻理解Garboczi(Garboczi and Day, 1995; Garboczi and Berryman,2001)工作的数学与物理基本原理，本文基于最小位能原理详细地推导了三维数字岩心数据体在初始应变条件下，求取弹性体内部弹性位移场的有限元方程，进而获得弹性体静态弹性模量的原理.同时也提出了对该算法进一步优化与效率升级的研究思路与方案.

1 样品描述与CT扫描

本文所测试的7块样品均为白云岩样品，直径均为38 mm，7块白云岩样品的基本信息如表1所示.使用Micro-CT进行CT扫描成像，图像分辨率可达每体素20.7678 μm.我们对取自同柱塞下的碎块进行X射线衍射(XRD)分析，如表1所示，可以看到大部分样品含有90%的白云石矿物，而其他的矿物则主要以石英矿物为主，因此本研究所测试的样品主要由白云石组成，在以下的研究中将不同尺度下的样品均视作只含白云石这一单一矿物.图1展示了7块样品CT扫描成像的横向切片(平行于圆柱面的切片)，可以看到这些白云岩样品具有非常复杂的孔隙结构类型，也一定程度地展示了这些样品具有较强的非均质性，给碳酸盐岩储层预测带来巨大的困难与挑战.关于7块样品更加详细的孔隙结构类型描述与分析将在系列文章下篇中讨论.本文中我们以3-1#白云岩岩心作为例子来展示二值化图像处理的过程，并最终建立了针对于碳酸盐岩数字岩心数据图像处理的工作流程，这是进一步实施碳酸盐岩基于数字岩心弹性性质模拟的关键一步.

表1 样品基本信息Table 1 Sample description

2 数字岩心图像处理

CT扫描原始图像需要经过一系列图像处理才能提取到我们感兴趣的矿物颗粒排布与孔隙结构等有用信息.这里所说的图像处理目标并不是完美还原高质量图像，而是针对我们感兴趣的信息进行一系列增强以及提取.常用的图像处理手段及流程包括对比度增强、滤波去噪、相边缘增强以及图像分割.对于不同类型不同工区的岩样，扫描得到的图像特征千变万化，这就需要因地制宜的选择合适的处理手段，本文在以上处理流程的每个部分都应用了多种处理技术进行尝试，经过优选确定了适用于本研究7块碳酸盐岩样品的处理技术，最终通过氦气实测孔隙度标定验证了图像处理的准确性.

2.1 对比度增强

首先对CT扫描的原始图像进行剪裁，即选取边长为1000体素的正方体.剪裁后的CT图像灰阶主要分布在非常低值区域，从图像的直观观测上显示为图像信息都比较暗，见图2a.这样窄分布的灰阶会给后续的图像分割造成困难，因此需要对图像进行对比度增强.对比度增强操作也就是通过灰度变换将原本窄分布的灰阶直方图变换成宽分布的直方图，拓宽孔隙相与固体相间的过渡带的灰阶分布，这样就能更好地方便后续图像分割阈值的选取.

针对样品原始CT图像的灰阶直方图分布特点，先将所有像素的灰度值统一降低使最小灰度值为零.然后采用变换函数为线性方程的灰度变换方法来对CT图像上所有像素点进行线性放大，使其最大灰度值为16位图像的灰阶最大值即65535.我们使用灰度变换公式(1)来实现上述功能：

(1)

其中，f(x,y)表示原始二维图像上坐标(x,y)处的像素点灰度值，g(x,y)表示经灰度变换后的该像素点灰度值，a、b、c、d均为常数.

对比度增强处理后图像的灰阶重新分布结果可见图3，原来非常窄的灰阶分布(黑色数据点)被拓宽到全灰阶分布(红色数据点)，且孔隙相和固体相的波峰分布特征被明显增强.孔隙与固体过渡带都得到很好的灰阶分布拓宽，从而完成了合理的图像对比度增强，为后续阈值选取打下了良好的基础.

图1 轴向CT成像切片Fig.1 Axial CT imaging slice

图2 对比度增强过程(a) 原始扫描图像切片； (b) 切块后(边长为1000体素的正方体)原始图像切片； (c) 对比度增强结果.Fig.2 Contrast enhancement process(a) Original scanned image slice; (b) Original image slice after slicing (square with side length of 1000 pixels); (c) Contrast enhancement results.

图3 线性拉伸法的灰阶重新分布结果Fig.3 Grayscale redistribution results for linear stretching

2.2 各向异性扩散滤波

由于在图像处理中像岩石的裂缝、纹理这些重要的微观结构信息会对岩石的弹性性质产生显著的影响，因此，在对图像进行滤波处理时要对裂缝、纹理等这些重要的信息进行妥善处理，这一点对于碳酸盐岩这种具有复杂孔隙结构类型的岩石类型而言尤为重要.以往滤波包括中值滤波、均值滤波、高斯滤波等这些常用的算法均属于全局滤波算法，是统一对待图像上每一个像素点，对于相对均质各向同性的碎屑岩而言这些算法基本可以满足图像处理中滤波的需求，而对于孔隙结构类型复杂的碳酸盐岩而言，这些常规算法势必会将裂缝、纹理等信息平滑掉，造成微观信息损失.所以，需要采用更适用的滤波算法，达到只对噪声信号进行滤除而保留裂缝、纹理等重要细节信息的目的.利用碳酸盐岩数字岩心数据，我们在对包括中值滤波、均值滤波、以及高斯滤波等常规全局滤波算法进行了大量的图像滤波实验基础上，对Perona和Malik(1990)提出的各向异性扩散滤波算法也进行了图像处理实验，对其算法中的参数也进行了一定优化，使该算法特别适用于具有复杂孔隙结构类型的碳酸盐岩数字岩心数据，各向异性扩散滤波核心算法如公式(2)—(4)所示：

(2)

(3)

(4)

图4显示了对比度增强处理后的CT原图，以及分别经中值滤波、均质滤波、高斯滤波以及各向异性扩散滤波后的处理结果，可以看到经各向异性扩散滤波后的效果较好，固体颗粒内部与孔隙内部的噪声信号被成功平滑掉，而固体颗粒与孔隙间的边缘信号得到了很好地保留.同时方便读者理解，如图5所示，我们也给出了“图像梯度阈值参数”K与“边缘品质参数”的确定思路，这两个参数在具体处理过程中，需要仔细评估与测试才能使得各向异性扩散滤波获得最佳效果.

2.3 边缘检测增强

边缘检测增强的目标是为了使图像边缘更清晰，从而准确地实现图像分割这一最关键步骤，对于碳酸盐岩数字岩心研究而言，由于刻画与突出复杂孔隙结构的需求，这一步骤也显得尤为重要.从图像学研究的角度而言，边缘增强本质上是对图像高频分量的提取，而边缘增强的主要困难在于锐化滤波器特别容易放大图像中所有噪声.图像高频分量的提取有两种做法：一种是通过低通滤波，用原图减去低频信号获得高频信号，常用的有unsharp模板滤波(Sheppard et al., 2004)；另一种为边缘检测法，即用高通滤波器直接获得图像的高频分量.对于第一种基于低通滤波的unsharp模板滤波方法由三个操作步骤组成：(a)用类似于高斯算子、平均算子等的平滑算子将原始图像模糊化；(b)原始图像减去模糊图像得到模板值；(c)模板乘上增强系数后累加到原始图像上.在针对于碳酸盐岩CT图像处理中，我们首先尝试使用该方法进行了刻画复杂孔隙结构的边缘增强处理，结果如图6b所示.对于第二种基于高频滤波器的边缘检测法，边缘增强处理的结果如图6c所示.比较图6b与图6c，可以看到基于高频滤波器的边缘检测法效果非常好，可以很完整地将固体颗粒与孔隙间的边缘区域识别出来，在此基础上再进行图像二值化分割将大大降低分割的不确定性，从而获得更好的二值化图像分割效果.

如上基于低通滤波的unsharp模板法与基于高频滤波器的边缘检测法在针对碳酸盐岩数字岩心数据处理中产生的差异的原因，分析如下.unsharp模板缺乏一定的理论基础，尽管在实践中unsharp模板法证明了其在边缘锐化方面的有效性，而且不会过度放大噪声信号，然而，unsharp的相增强边缘的增强像素点不太稳定，unsharp模板滤波严重依赖于平滑程度与原图差异的限制，因此它的增强效果没有直接使用边缘检测算子求图像梯度那么明显.此外unsharp采用的是高斯算子进行全局平滑，这种全局平滑本身就不区分像纹理、裂缝等有效信息，因此unsharp模板不适用于真实碳酸盐岩CT图像处理.

2.4 二值化图像分割

为了将孔隙结构从CT图像中提取出来，就必须识别每张图像中的孔隙像素，这个识别过程在图像处理中叫做图像分割.图像分割技术一般分为几何形状分割法和聚类分割法(Otsu,2007).前者是分析灰度直方图几何形状来确定分割阈值的方法，而后者是通过图像中两组数据间的统计属性差异来确定最佳阈值的方法.聚类分割法有如下三个步骤：(1)图像中每个像素点都对应一个灰度值，Otsu算法则将图像中所有像素点的灰度值视作一个数据集合；(2)CT图像是灰度图像，其灰度分布一般有8bit(0～255)或16bit(0～65535)这两种，以8bit为例，阈值从0取到255共256个值，每个阈值都将数据集合分为两类；(3)计算每个阈值分类后两类数据的类间方差与类内方差之比，比值最大点所对应的阈值便是Otsu法找到的阈值.与普通阈值分割思路类似，将分出的两类数据的灰度值进行重新赋值，一般是分别赋予最大差距值，这个过程称为二值化处理.Otsu算法由于其基于灰度直方图上单一阈值的特性，尤其适合单矿物样品(Faisal et al., 2017),而本研究中测试的样品正是只含白云石这一单一矿物的样品，因此本研究中使用Otsu算法对CT图像进行分割.图7展示了使用Otsu算法进行图像分割的二值化结果，黑色表示孔隙，灰白色表示固体颗粒.

图4 多种滤波方法处理结果对比(a) 对比度增强后CT原图； (b) 中值滤波； (c) 均值滤波； (d) 高斯滤波； (e) 各向异性扩散滤波.Fig.4 Comparison of processing results of multiple filtering methods(a) CT original image after contrast enhancement; (b) Median filter; (c) Mean filter; (d) Gaussian filter; (e) Anisotropic diffusion filtering.

图5 图像梯度阈值参数与边缘品质参数的确定(a) 图像梯度阈值参数K的选取方案； (b) 边缘品质参数的选取.Fig.5 Determination of image gradient threshold parameters and edge quality parameters (a) Selection scheme of the image gradient threshold parameter K; (b) Selection of the edge quality parameter.

图6 边缘检测增强结果(a) 滤波后CT图像； (b) 基于低通滤波的unsharp模板法边缘增强结果； (c) 基于高频滤波器的边缘检测法增强结果.Fig.6 Edge detection enhancement results(a) Filtered CT image; (b) Edge enhancement results of the unsharp template method based on low-pass filtering; (c) Enhanced results from edge detection based on high-frequency filters.

图8a是3-1白云岩样品建立的二值化分割后的三维数字岩心模型，图8b为从建立的三维数字岩心模型中提取而出的孔隙结构.从图8b所示的分割图像中，我们可以看到红色很充分地填充了原始切片上的所有孔.实验室氦气测得孔隙度为3.711%，而分割后得到成像孔隙度略小于氦气孔隙度，其值为2.297%.这是因为碳酸盐岩具有非常强的非均质性，其孔径可以小至几百个纳米而大至几个厘米.而且，图像分辨率与成像视域总有着不可协调的矛盾，若要使得分辨率越高则成像视域就会变小.所以一旦视域固定，那么其成像分辨率也是唯一不变的.对于成像孔隙度略小于实验孔隙度这样的现象一个较合理的解释是：碳酸盐岩中总有一些孔隙，其孔径甚至比CT分辨率还要小而无法成像，因此由CT成像估算的孔隙度会小于实验室氦气测量的孔隙度.由于微孔结构不能被完全分辨，CT图像上颗粒与微孔接触区域会表现出模糊状.这样的话分割过程就会产生不可避免的误差.而相对可信的分割过程通常会使分割后的孔隙度偏低.分割过程通常会将颗粒接触划分为骨架的一部分，从而丢失柔软部分的信息，这使得数字岩心比实际的岩石样品更“硬”一些.Eberhart-Phillips等(1989)对不同围压下砂岩进行过实验测试研究，并观察到速度会随围压增加而呈指数增大.这是因为随着围压的增大，颗粒接触间的微孔也会随之逐渐闭合.由于数字岩心与围压下岩心这两种情况下微孔都会消失，所以我们尝试将数字岩心模拟结果与超声下不同围压的测试结果进行比较.

我们使用上文提到的完全相同的图像处理流程来对剩余6块白云岩CT数据进行处理，并得到相应二值化后的三维数字岩心模型.对这7块白云岩，在实验室条件下利用氦气孔隙度渗透率测量仪对白云岩样品的孔隙度进行了测试，并借此来验证所建立三维数字岩心模型的准确性，测得数据见表2.

表2 样品氦气测量孔隙度与图像计算孔隙度物性表Table 2 Helium porosity and image porosity

图7 CT图像分割过程图(a) 图像预处理后CT图； (b) 图像分割结果.Fig.7 Diagram of CT image segmentation process(a) CT image after image pre-processing; (b) Image segmentation result.

从表2中可以看到这7块白云岩的数字岩心计算孔隙度都要略低于实验室氦气孔隙度测量值.如前述解释，由于CT成像分辨率的限制，总是有一部分小于成像分辨率的孔无法在CT图像上清晰显示，所以造成数字岩心成像孔隙度会略小于实验室氦气测量孔隙度.这种现象如图9所示，在CT图像上颗粒与微孔接触区域会表现出模糊状，从左上角选择一块区域如图9a所示，将其进行放大见图9b，可以看到红色部分是识别出来的孔隙空间，灰白色部分是白云石基质，而灰黑色部分就是基质与孔隙接触区域，也就是微孔结构存在的地方.由于低于成像分辨率的微孔区域存在，这样分割过程就会产生不可避免的误差.而相对可信的分割过程通常会使分割后的孔隙度偏低，所以计算孔隙度略小于实测孔隙度是比较合理的.因此通过实验室氦气孔隙度标定，我们得到了准确可靠的白云岩三维数字岩心模型，并最终针对碳酸盐岩数字岩心数据，建立了如上合理的图像处理与二值化分割的处理流程以及各步骤中合理的参数设置方案.

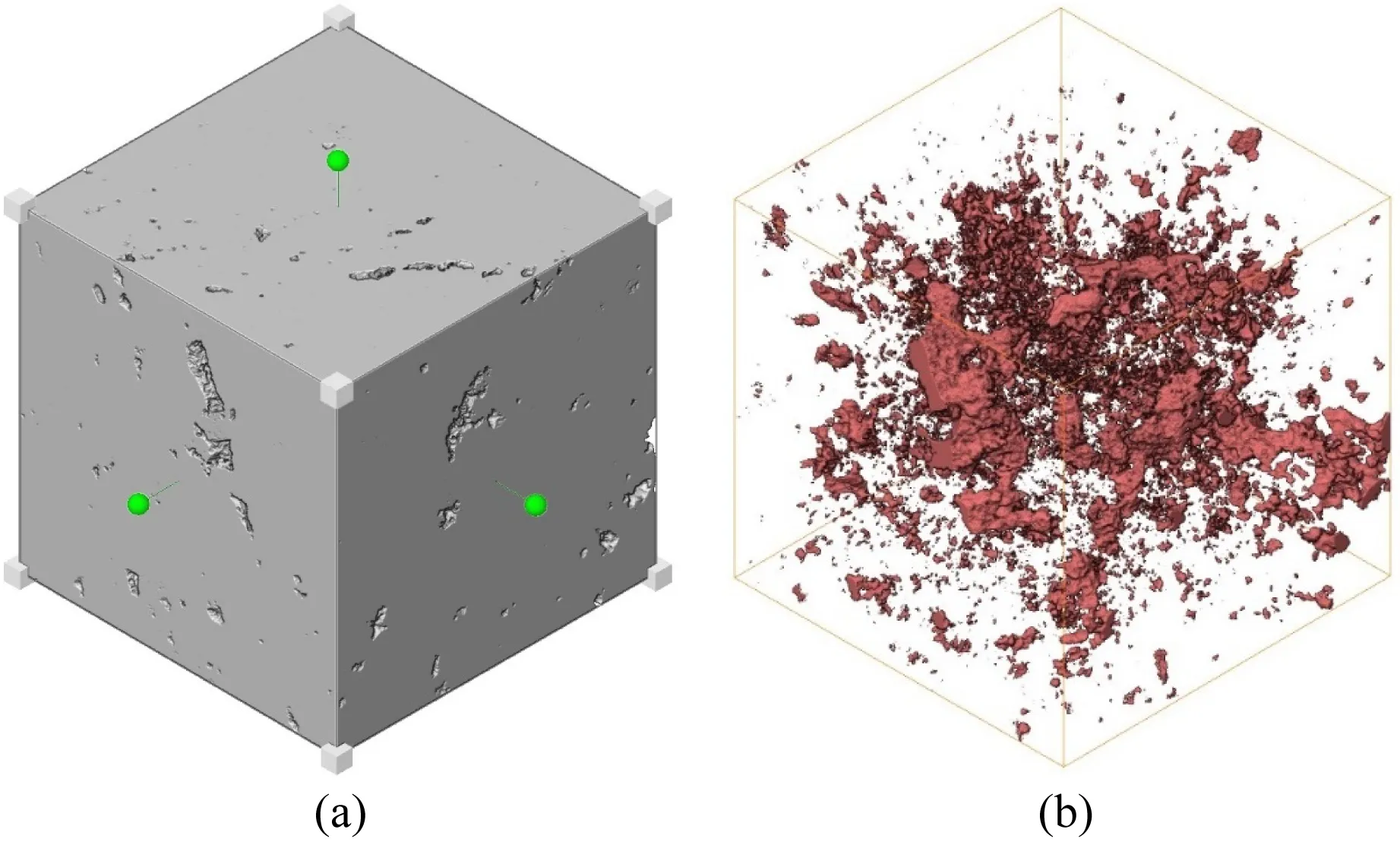
图8 二值化图像分割结果(a) 分割得到的孔隙结构； (b) 分割得到的岩石骨架.Fig.8 Binarized image segmentation results(a) Pore structure obtained by segmentation; (b) Rock matrix obtained by segmentation.

图9 (a) 3-1号白云岩样品CT图像分割过程图； (b) 分割过程部分视域放大图Fig.9 (a) Illustration of CT image segmentation process of 3-1 dolomite sample; (b) Magnified view of part of the segmentation process

3 弹性性质模拟理论框架

物体在外力作用下要产生形变，对于完全弹性体而言，当外力撤除后物体将恢复到受力前的状态.从这一点出发，我们可以把外力作用使物体发生形变看成是外力对物体做功，而外力撤除物体恢复原来状态过程看成是物体的释能过程.因此，对完全弹性物体，当其发生变形后将在弹性体内储存一定的能量，这个能量就是应变位能.笛卡尔坐标系下，单位体积单元内的应变位能表达式如下：

(5)

此时，系统的总能量为

(6)

其中

ε=[ε11,ε22,ε33,ε13,ε23,ε12]T

=[e11,e22,e33,2e13,2e23,2e12]T,

(7)

σ=[σ11,σ22,σ33,σ13,σ23,σ12]T,

(8)

ε与σ分别为点(x,y,z)处的应变张量与应力张量，此外，由Voigt表示法有

ε1→ε11,ε2→ε22,ε3→ε33,

ε4→ε23,ε5→ε13,ε6→ε12.

(9)

σ1→σ11,σ2→σ22,σ3→σ33,

这第二种“正在形成或者继续重建”的结构与存在论中的建构结构似乎具有某些相通之处。前提是，如果我们以存在主义观点而非生物主义观点来给这第二种结构定下基调——从人的活动即“此在”结构出发，就可以将“民间故事活动”看成一个“开放的活的”结构系统，始终处于未封闭的形成过程中，并通过不断的交流进行调节达到暂时平衡。[注]此观点详见张琼洁《当代民间故事活动价值发生研究》，《民族文学研究》，2018年，第1期。

σ4→σ23,σ5→σ13,σ6→σ12.

(10)

根据胡克定律

σ=C·ε或

这样方程(6)改写为

(12)

其中，C=Cij(i,j=1,2,…,6)为6行6列的弹性参数张量.

另外一方面，在对原始碳酸盐岩CT数据进行图像处理后便建立了可靠的三维数字岩心模型，对于三维数字岩心模型可以使用如图10a所示的六面体网格进行有限单元法网格剖分，也可以使用四面体网格对三维数字岩心数据体进行剖分，如图10b所示.两种网格剖分方案各有利弊，六面体网格剖分方案最大的优势在于由于其网格的规则性，从而在有限元控制方程形成时比较容易地实施刚度矩阵的组集与合成，此外，六面体网格的剖分方案使得周期性边界条件的加载变得更加容易.四面体网格剖分方案的优点在于对于更加复杂的三维数字岩心数据体可以获得更加精细的剖分，然而，该种剖分方案对边界条件的加载提出了更高的要求，此外在计算效率上提出了更高的挑战.我们在Garboczi 和Day(1995)工作的基础上，对两种剖分方案均进行了发展与算法优化，可以得到更为高精度与高效率的计算结果.

物理上，问题的本质就在于对一个给定的三维数字岩心数据体施加一个初始应变εini=[ε11,ε22,ε33,ε13,ε23,ε12]T，从而评价与求取使得方程(6)所示的系统总能量达到极小的在三维数字岩心数据体上的位移分布场.数学上，就是将弹性位移场分布的求解问题转化为最小位能原理的问题，这就是有限元中经典的泛函求极值问题，最终可获得三维数字岩心数据体在受到初始静态应变εini=[ε11,ε22,ε33,ε13,ε23,ε12]T后系统的弹性位移场分布，以及三维数字岩心数据体代表的岩石在宏观上表现出来的6个方向的应力σxx,σyy,σzz,σxz,σyz,σxy与6个方向的应变εxx,εyy,εzz,εxz,εyz,εxy，进而可求得宏观上表现出来的静态等效弹性模量.

图10 三维数字岩心数据体的有限元剖分(a) 六面体网格剖分数字岩心三维数据体； (b) 四面体网格剖分数字岩心三维数据体.Fig.10 Finite element dissection of a 3D digital core data body(a) Hexahedral grid dissection of the digital core 3D data body; (b) Tetrahedral grid dissection of the digital core 3D data body.

接下来我们用Garboczi和Day(1995)提出的线弹性有限元法，以六面体网格剖分方案为例，详细给出求取弹性位移场的有限元控制方程形成的推导过程.如图10a所示，使用六面体网格剖分三维数字岩心数据体时，每个六面体视作一个体素，也为一个线弹性有限元网格，并按照如图10所示的编号规则编为①—⑧号，根据有限单元法思想此时该体素内的位移u有如下表达式：

(13)

N1=(1-x)(1-y)(1-z),

N2=x(1-y)(1-z),

N3=xy(1-z),

N4=(1-x)y(1-z),

N5=(1-x)(1-y)z,

N6=x(1-y)z,

N7=xyz,

N8=(1-x)yz.

(14)

可进一步将方程(13)展开如下：

=[u11u21u31u12u22u32u13u23u33u14u24u34u15u25u35u16u26u36u17u27u37u18u28u38]T,

(15)

其中，N=[N1IN2IN3IN4IN5IN6IN7IN8I]为3行24列；

此时，应变ε可表示为

ε=L(Nue)=(LN)ue,

(16)

其中，L为梯度算子，其表达式如下：

(17)

将公式(15)代入公式(12)，便可得到在单个体素中存储的应变位能，其表达式如下：

(18)

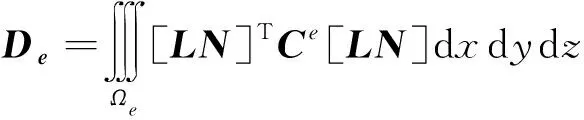
(19)

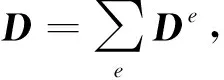
在计算三维数字岩心代表的系统储存的应变位能时，需要施加一定形式的边界条件，考虑在系统的边界单元(体素)上存在初始位移Δub，此时方程(18)变为如下形式：

(20)

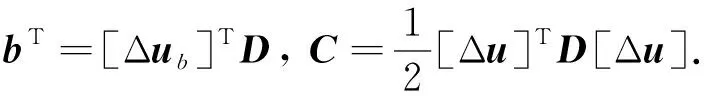
Du=-b.

(21)

解此方程便可求取获得各节点上的位移矢量u，并根据方程(11)以及方程(15)得到三维数字岩心数据体代表的岩石内部的应变分布以及应力分布，以及最终获取三维数字岩心数据体代表的岩石在宏观上表现出来的6个方向的应力σxx,σyy,σzz,σxz,σyz,σxy与6个方向的应变εxx,εyy,εzz,εxz,εyz,εxy，进而可求得宏观上表现出来的静态等效弹性模量.

4 弹性性质模拟及验证

利用第3节提出的理论框架与数值模拟流程，我们对7块白云岩样品都进行了弹性性质的数值模拟，仍然以3-1白云岩样品为例就利用数字岩心数据进行弹性性质模拟、实验验证以及需要注意的问题进行讨论.

碳酸盐岩非均质性强、孔隙结构复杂，以往的研究发现数值结果与实验数据很难从定量的角度一一对应上.Dvorkin等(2011)提出由数字岩心内部非均质的子数据集模拟得到的数据点组成的趋势线在多个尺度上都有效，这样的趋势线不会随着空间位置和尺度改变而变化太大.本研究中为了解决数字岩心模拟结果与实验数据的匹配问题(利用三维数字岩心进行弹性性质模拟时其结果应该对应实际物理实验哪一围压下的结果)，按照如下步骤实施：以3-1白云岩样品为例，一方面，我们对此样品进行变围压(以5 MPa为步长从0 MPa逐步增加到20 MPa)超声波时差法测量纵横波速度，结果如图11所示，可以看到纵横波速度与弹性模量均随围压的增加而快速增加，造成这种现象是因为随着围压的增大，岩石颗粒接触间的微孔由于受全方位应力的作用而逐渐闭合使岩石变得越来越硬.另一方面，我们利用Dvorkin等(2011)提出的划分三维数字岩心子网格的思路，将3-1白云岩的三维数字岩心数据体切块得到尺寸为250×250×250立方体素的子块化数据(见图12)，再对每个子块化数据进行弹性性质模拟，之后从模拟数据中挑选与实验孔隙度接近的8个子块体数据点绘制趋势线(见图13黑色数据点).图中不同颜色数据点代表测试样品在不同围压下实验室超声测试数据，从绿色到红色表示围压以5 MPa为步长从0 MPa逐步增加到20 MPa.从图13可以看到由数字岩心模拟数据拟合的趋势线介于10 MPa与15 MPa超声数据之间，但非常靠近15 MPa围压超声数据.模拟结果与实验数据间的百分比差异非常小(见表3)，这也在一定程度上验证了本研究基于三维数字岩心进行弹性参数模拟工作的合理性与准确性.

表3 白云岩样品3-1超声数据与弹性模拟结果对比Table 3 Comparison of ultrasound data and elastic simulation results for dolomite samples 3-1

实际上我们需要指出，在利用三维数字岩心数据进行弹性性质模拟时，对于不同岩性、不同区块、不同胶结类型、不同压实的岩石样品，首先需要重视成像分辨率的问题.实际上，小于成像分辨率的微孔细节，其一般存在于颗粒间接触，在CT图像上表现出模糊状.而可信的图像处理是忽略这些超出成像能力的信息，也就是说我们得到的数字岩心模型实际上是忽略了低于成像分辨率的微孔信息的宏孔结构，这使得数字岩心比实际的岩石样品更“硬”一些.

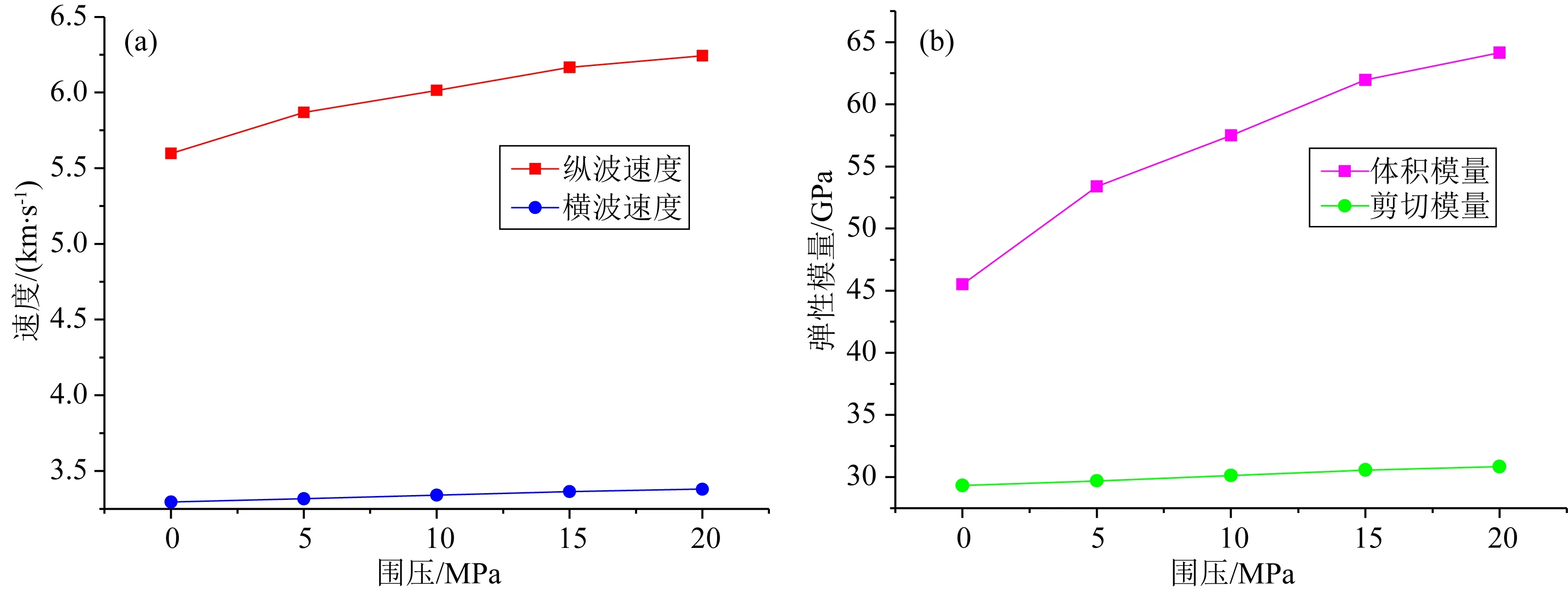
图11 白云岩3-1样品速度和弹性模量随围压变化关系图Fig.11 Variation of velocity and elastic modulus of dolomite 3-1 sample with confining pressure

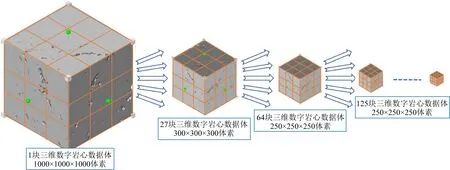
图12 白云岩3-1三维数字岩心数据体子网格化Fig.12 Dolomite 3-1 3D digital core data body sub-block meshing

图13 模拟和实验得到的纵波速度与孔隙度交会图颜色从绿色逐渐变为红色代表增加的围压.Fig.13 Simulated and experimentally obtained primary wave velocity versus porosity intersection plotsThe gradual change in color from green to red represents the increase in circumferential pressure.

与此相类似，在自然界中的岩石在受静水压力(等效于围压)下，岩石内部结构发生改变而使得岩石整体性质改变.Eberhart-Phillips等(1989)对不同围压下砂岩进行过实验测试研究，观察到速度会随围压增加而呈指数增大.已有学者做了类似的围压下天然样品受力的实验，Zhang等(2016)通过微米CT设备对煤炭样品在围压下的内部结构进行了成像，其中有两条非常明显的裂缝也就是常说的软孔，在加载围压后受力闭合了.这样从实验的角度就验证了天然样品在围压下微孔发生闭合，天然样品内部结构变得更加坚硬使得抗压缩系数增大，弹性模量与纵横波速度增大.数字岩心由于其分辨率的缘故以及岩心受到围压这两种情况微孔都会消失或者部分消失，因此，基于数字岩心弹性性质的数值模拟结果需要与实验室变围压下测试数据进行比较，这在一方面说明了本研究所建立的三维数字岩心模型能揭示某围压下岩石内部结构受力情况时的弹性性质，另外一方面也验证了我们建立的关于碳酸盐岩数字岩心图像处理流程的合理性以及在此基础上弹性性质模拟结果的有效性.

5 结论

本文提出了一套适用于碳酸盐岩的图像处理流程来建立准确可信的数字岩心模型.在图像处理部分，本文改进了各向异性扩散滤波的输入参数选择问题，明确了“图像梯度阈值参数”K与“边缘品质参数”的确定思路，使得图像滤波效果达到最好.同时使用梯度算子提取基质与孔隙的相边缘，并增强相边缘信号.在此基础上选择图像分割算法Otsu法来完成图像处理全部流程，得到最佳处理方案的数字岩心模型，最后使用实验室测试孔隙度验证了模型的准确性.

数字岩心弹性模拟方面，为了方便一般作者深刻理解Garboczi(Garboczi and Day, 1995； Garboczi and Berryman,2001)工作的数学与物理基本原理，本文基于最小位能原理详细地推导了三维数字岩心数据体在初始应变条件下，求取弹性体内部弹性位移场的有限元控制方程，进而获得弹性体静态弹性模量的原理.在此基础上，考虑数字岩心数据体在图像处理过程中由于忽略了低于成像分辨率的微孔而使得所建立的数字岩心模型比实际岩心更硬，而围压载荷下岩石中软孔闭合也会使得岩石结构变硬.本研究将这两者联系起来，发现数字岩心模拟结果与15 MPa下超声数据对应得非常好，百分比误差低，因此验证了本文所建立的三维数字岩心模型能揭示围压下岩石内部结构受力情况以及验证碳酸盐岩数字岩心模拟结果的有效性.可以预期本文所建立的针对碳酸盐岩的二值化图像处理流程，与基于数字岩心数据体的碳酸盐岩弹性性质模拟的研究成果，可以为进一步研究适用于碳酸盐岩的岩石物理模型的建立、流体替换模型，以及提高碳酸盐岩储层预测的定量化解释水平奠定基础.