政企双层规划下考虑碳配额的供应链网络优化

田雪林，程发新

（江苏大学 管理学院，江苏 镇江 212013）

0 引言

根据欧盟碳排放交易体系的经验，碳配额配置过程不仅关乎碳配额交易市场的效率，也会很大程度地影响社会福利[1]。如何合理配置碳配额，一直是政府部门关注的重点问题[2]。对供应链企业来说，碳配额已经成为一种可交易的生产要素，将影响到生产运营的各个环节，已成为供应链低碳化运营决策的重要关切点[3]。低碳化运营决策取决于政府部门配置碳配额决策，链主企业需要积极与政府部门互动，以达到政企决策协同演进的效果[4]。在政企互动决策过程中，政府部门和链主企业处于不同的决策层级，政府部门作为上层决策者，主要考虑合理地配置碳配额。而处于下层决策的链主企业，则根据碳配额来引导供应链其他成员决策，旨在实现供应链网络总成本和碳排放最小化[5]。

关于环境政策下供应链网络优化研究，现有文献仅将环境政策作为外生变量，纳入供应链网络优化的规划模型中[6-8]，鲜有文献同时考虑政府部门和供应链企业两个不同决策主体的互动。考虑政府部门和供应链企业作为不同决策主体的供应链网络优化还处于起步阶段，仍有进一步拓展的空间：一是现有研究尽管考虑了政府部门决策对供应链企业经营决策的影响，但均未考虑企业经营策略对政府部门决策的反馈作用。例如，Chalmardi等[9]针对清洁生产技术的企业进行补贴，建立政企双层规划模型以优化供应链网络，但该研究尚未涉及清洁生产技术减排效果对补贴政策的影响。二是在政企决策过程中，既有研究尚未明确链主企业对其它供应链企业的主导作用。事实上，链主企业作为碳排放主体，不仅需要承担决策风险，还需引导供应链其它成员的经营决策[10]。三是政企双层规划下的供应链网络优化的相关研究，均假设市场需求确定，这与供应链企业面临的实际经营环境不相符[11]。

基于此，本文研究政企双层规划下考虑碳配额的供应链网络优化问题，与既有文献不同之处为：（1）考虑链主企业经营策略决策对政府部门碳配额的反馈作用，探索配置碳配额的互动决策过程，这将拓展文献[9]的研究范围；（2）基于链主企业是碳排放主体并且需要承担决策风险的事实，明确链主企业对其它成员决策的主导作用，而文献[9]却忽视链主企业的主导作用。（3）政企双层规划下将市场需求不确定纳入供应链网络优化模型，相关的研究还比较少见。由此，本文假设市场需求不确定，构建政企互动决策下的双层规划模型，以优化供应链网络总成本和碳排放，采用多目标粒子群优化算法（MOPSO）求解双层规划模型，探索碳配额和市场需求不确定置信水平变化对供应链网络Pareto最优解集的影响。

1 问题描述与研究假设

1.1 问题描述

本文设定链主企业为双寡头制造商，由此对政企双层互动决策过程进行描述。政府部门首先对双寡头制造商配置初始碳配额，接着双寡头制造商参考初始碳配额决策，将“理想初始碳配额”反馈给政府部门，这一点既有文献几乎没有涉及。最后，政府部门根据双寡头制造商的“理想初始碳配额”配置最终碳配额。假设碳交易收支由双寡头制造商承担，这主要是因为双寡头制造商作为碳排放主体，需要承担供应链碳排放交易的损益，既而引导其它企业的经营决策。具体如图1所示。

供应链网络拟包括供应商、双寡头制造商、分销商和销售商。其运作过程主要为：供应商供应生产所需原材料，双寡头制造商制定生产经营策略生产产品，并将产成品运往分销商，分销商再将产成品运往各销售商进行销售。本文考虑不确定市场需求环境下，政府部门和双寡头制造商两层决策主体，建立双层规划模型，以优化供应链网络总成本和碳排放。

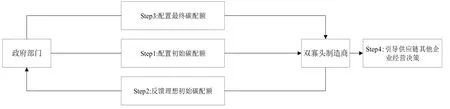
图1 政企双层决策过程

1.2 研究假设

从问题描述出发，在不改变问题实质的前提下，对一些复杂条件加以简化，提出相关的基本假设：

（1）假设供应链网络中存在s个备选供应商s={1,2,...,S}、双寡头制造商（m1和m2）、d个备选分销商d={1,2,...,D}和c个销售商c={1,2,...,C}，各节点构成供应链网络。其中，销售商位置固定，不单独考虑其设施选址。

（2）各备选供应商、双寡头制造商和备选分销商处理能力上限分别为Caps、Capm1和Capm2及Capd。

（3）基于经济最优和公平兼顾的碳配额配置策略函数中，政府部门通过经济贡献指数γ和污染承担指数ε兼顾公平。同时，政府部门从经济贡献指数γ考虑，并设定初始碳配额调整系数为θ[12]。

（4）双寡头制造商之间存在竞争合作关系[19]，假设他们的γ和ε相同。

（5）双寡头制造商处于同一市场，市场需求Demc不确定，且服从正态分布。

（6）政府部门仅对双寡头制造商配置碳配额，双寡头制造商承担整个供应链碳交易收支，并设定碳交易价格为P元/t。

2 双层规划模型构建

双层规划模型包括上层规划和下层规划。上层规划是政府部门为双寡头制造商配置碳配额，双寡头制造商参考初始碳配额决策，政府部门根据双寡头制造商决策结果配置最终碳配额，以控制碳排放。下层规划是双寡头制造商根据最终碳配额，引导供应链其它企业调整其经营策略，这主要是双寡头制造商承担供应链网络的碳交易收支，供应链网络碳排放最小化事关双寡头制造商的利益。

2.1 上层规划模型的碳配额

上层规划模型的目标是政府部门为双寡头制造商合理配置碳配额。为此，本文借鉴文献[12]的思路，对模型进行改进。根据经济最优和公平兼顾原则配置碳配额，构建碳配额函数：

式（1）中，σ表示政府部门考虑双寡头制造商反馈的调整系数；ρ表示政府部门最终碳配额调整系数；A(1)表示双寡头制造商“理想初始碳配额”函数；A(2)表示政府部门根据双寡头制造商经济贡献指数γ调整初始碳配额的函数。

双寡头制造商“理想初始碳配额”函数表示为：

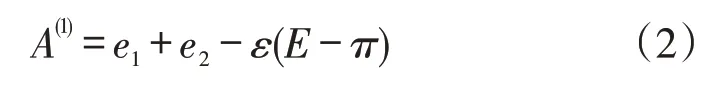
式（2）中，E表示总初始碳配额；e1、e2分别表示m1和m2的初始碳配额；ε为污染承担指数；π表示政府部门碳配额控制总量。

政府部门根据双寡头制造商经济贡献指数调整初始碳配额的函数为：

式（3）中，θ表示政府部门基于经济贡献指数对初始碳配额的调整系数；γ表示经济贡献指数；κ表示双寡头制造商的经济贡献指数之和。

根据文献[13]的思路，最终碳配额A在双寡头制造商之间分配：

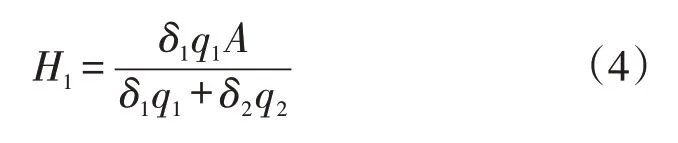
式（4）中，H1表示m1的最终碳配额；δ1为m1的碳排放量；q1表示m1的产量。

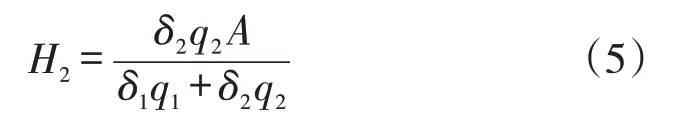
式（5）中，H2表示m2的最终碳配额；δ2为m2的碳排放量；q2表示m2的产量。

2.2 下层规划模型的目标函数及约束条件

下层规划模型的目标是双寡头制造商根据最终碳配额，以实现供应链网络碳排放和总成本最小化。

2.2.1 下层规划模型的目标函数确定

（1）碳排放最小化。供应链网络碳排放O由直接碳排放（ACOE）和间接碳排放（MCOE）之和减去最终碳配额A构成：

直接碳排放是由m1和m2产生碳排放与各节点间运输产生的碳排放加总构成：

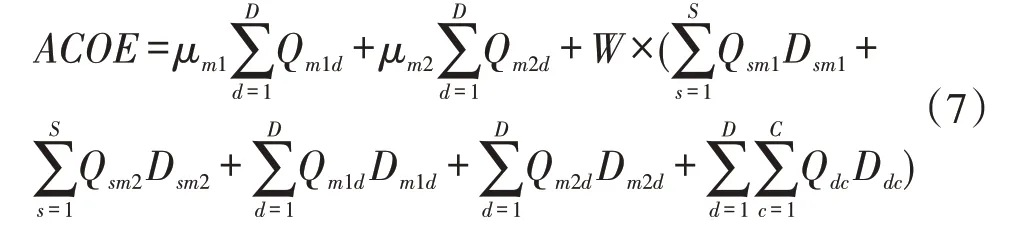
式（7）中，μm1和μm2分别表示m1和m2的单位产品碳排放因子，W表示单位距离运输碳排放因子；Qsm1、Qsm2、Qm1d、Qm2d和Qdc为决策变量，它们表示各节点间原材料、产品的运输量；Dsm1、Dsm2、Dm1d、Dm2d和Ddc分别表示各节点间的距离。

间接碳排放是由各节点运作过程中消耗的单位电能Es、Em1、Em2和Ed与各节点间物流量以及电力碳排放因子We乘积加总构成：

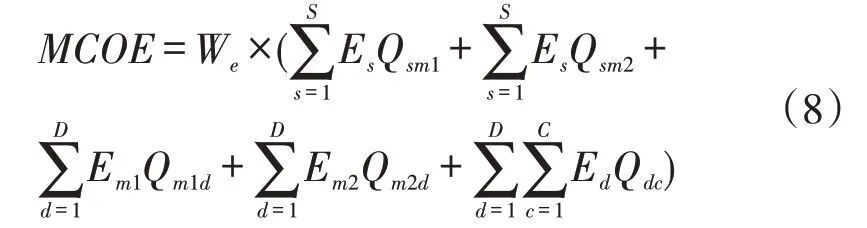
（2）总成本最小化。供应链网络总成本由固定建设成本（FC）、可变成本（AC）和碳交易收支（T rad）加总构成，目标函数为：

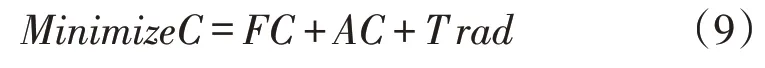
固定建设成本FC包括若干供应商、分销商建设的固定成本（FIs和FId）及其是否开设的决策变量（Ys和Id）的乘积之和与m1和m2的固定成本FIm1和FIm2、销售商的固定成本FIc加总构成：

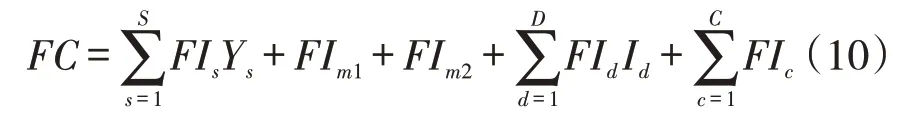
可变成本AC由各个节点运作成本与节点间运输成本加总构成：

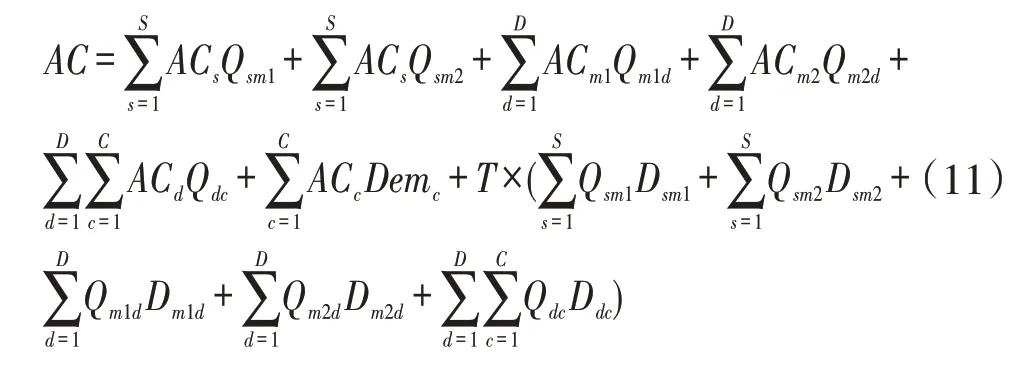
式（11）中，ACs、ACm1、ACm2、ACd和ACc分别表示各节点运作过程中的单位可变成本。Demc表示销售商产品需求量。T代表单位运输成本。Dsm1、Dsm2、Dm1d、Dm2d和Ddc表示各节点间运输距离。

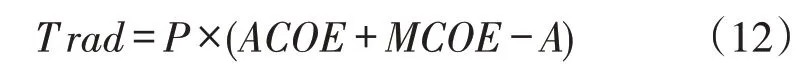
式（12）中，P表示碳交易价格，若ACOE与MCOE之和大于A，则m1和m2需要购买碳配额以承担损失。反之，m1和m2出售剩余碳配额以获益。

2.2.2 下层规划模型的约束条件。从下层规划模型的目标函数出发，在流量约束、容量约束以及决策变量约束范围内寻求可行解，从而优化供应链网络的总成本和碳排放。

（1）流量约束。供应商将原材料Qsm1、Qsm2运往m1和m2，且m1和m2生产过程中不考虑生产损耗，将其表示为：

m1和m2运往分销商的产品数量Qm1d、Qm2d与分销商运往销售商的产品数量Qdc相等，则：

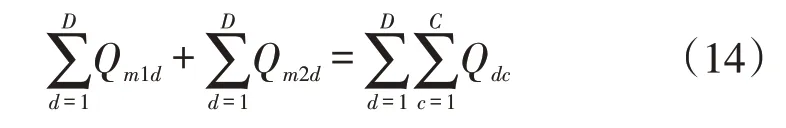
第c个销售商从分销商运输产品数量满足需求量，则流量约束表示为：

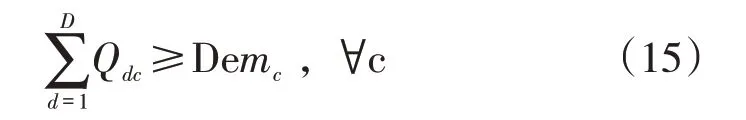
（2）容量约束。第s个供应商供应给m1和m2的部件不超过其原料开采能力：

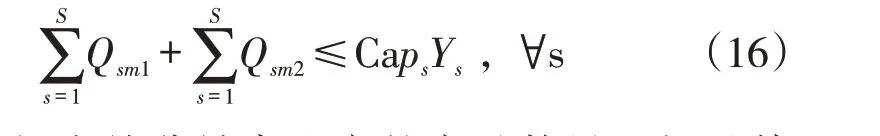
m1为批发给分销商生产的产品数量不超过其生产能力：

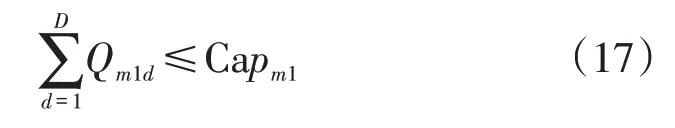
m2为批发给分销商生产的产品数量不超过其生产能力：

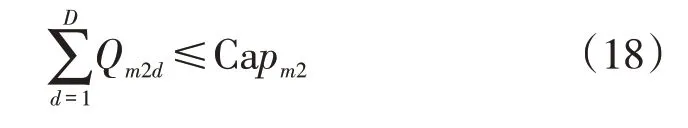
第d个分销商运往销售商的产品数量不超过其处理能力：

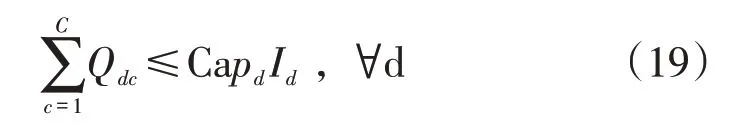
（3）决策变量约束。备选供应商和备选分销商只有开设或不开设两种情况：

各节点间物流运输量必须大于等于零：

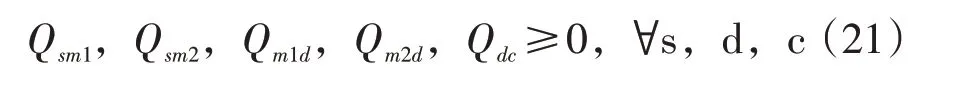
3 随机变量转化及规划模型的求解算法

在双层规划模型中，假设市场需求不确性，则约束条件（15）中需求量Demc为随机变量，且服从正态分布，需要进行参数转化。

3.1 市场需求不确定性参数转化

为求解该模型，本文采用随机机会约束规划的方法对约束条件（15）进行处理：

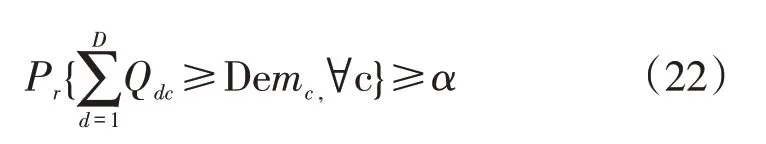
式（22）中，α为事先给定的置信水平。

根据确定性等价理论：

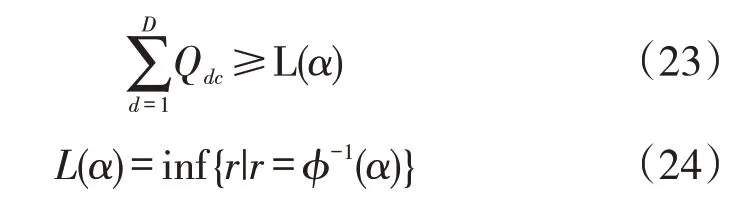
式（24）中，φ-1()表示第r个销售商需求量分布的逆函数，inf{}表示φ-1()的下确界。

3.2 双层规划模型的求解算法

随着供应链网络优化模型复杂度上升，采用精确算法求解模型既耗时又不可行。因此，针对不同研究背景，多目标供应链网络优化模型的求解仍是一个NP难题[14]。周向红等[15]认为多目标粒子群优化算法（MOPSO）采用高效的集群并行计算方式搜索，优化结果不限于单值解，且在一次运行中就能求得Pareto 最优解集，克服了传统方法的局限性。因此，本文拟采用MOPSO算法求解政企双层规划模型。

3.2.1 多目标粒子群优化算法。MOPSO算法是模拟生物群体行为而构造的一种随机搜索算法，源于对鸟类捕食行为的研究，算法中每个粒子的位置代表优化问题的一个潜在解。在B维搜索空间中，由N个粒子组成种群，每个粒子i 包含B维的位置向量xi=(xi1,xi2,...,xiB)T和速度向量vi=(vi1,vi2,...,viB)T。在搜索过程中，粒子记住其搜索到的历史最优位置pi=(pi1,pi2,...,piB)T。在每次迭代中，根据其个体历史最优位置pi(pBest) 以及全局最优位置pg(gBest)=(pg1,pg2,...,pgB)T不断更新自身速度和位置，实现种群进化。第i个b维粒子的速度和位置更新公式如下[16]：

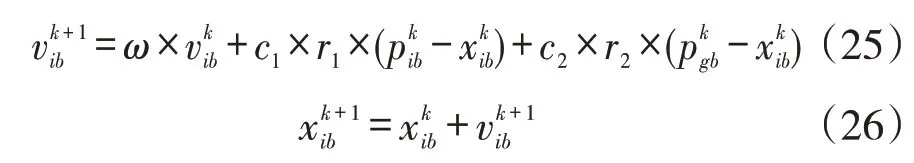
式（25）、式（26）中，k为当前迭代次数；c1和c2为加速度因子；ω是惯性权重，其大小对粒子群优化算法的收敛性能有很大影响；r1和r2为[0，1]间的随机数。

3.2.2 MOPSO算法实现步骤。借鉴文献[17]，需要对MOPSO算法进行改进以求解政企双层规划模型。通过两阶MOPSO 算法之间的协同迭代，以实现同步优化双层规划的上下层，最终求得双层规划模型的最优解。参考文献[18]，在MOPSO 算法中将种群规模设置为60，最大迭代次数为100，外部存档容量为100，个体学习因子c1和种群学习因子c2均设置为1.496，自适应扩张参数τ设为0.1。

求解双层规划模型MOPSO算法的具体步骤为：

Step1 初始化MOPSO算法中的参数，随机初始化种群中粒子的位置xi和速度vi，i ∈[1,N]，N为粒子的个数。

Step2 将第i个粒子的pBest设置为该粒子的当前位置，gBest设置为初始种群中最佳粒子的位置。

Step3 对粒子群中所有粒子的运行过程为：

（1）根据式（25）和式（26）更新粒子的位置和速度；

（2）将上层模型的解即粒子i的位置xi带入下层模型，利用MOPSO算法求得下层模型的最优解Yi；

（3）将(Xi,Yi)带入上层规划的目标函数，计算粒子i的适应度F(Xi,Yi)，i ∈[1,N]；

（4）如果粒子i的适应度优于其pBest的适应度，则该粒子的pBest更新为当前位置xi；对应于pBest的下层模型的最优解ypBest相应地更新为Yi；

（5）如果粒子i的适应度优于目前gBest的适应度，则gBest更新为当前位置xi，对应于gBest的下层模型最优解ygBest相应地更新为Yi。

Step4 判断是否达到最大迭代次数或者满足搜索精度要求的最优解，若是，转Step5,否则转Step3；

Step5 输出双层规划模型的最优解gBest和ygBest，并相应求出上下层规划目标函数值，算法运行结束。

4 算例分析

为验证模型和算法的有效性，本文以某市生态环境局对双寡头国有企业QM和SP配置碳配额为研究背景，验证政企双层规划模型并得出一些管理启示。

4.1 背景描述

国内某市生态环境局为推进化工行业实行碳交易，对市区所辖的双寡头制造商（QM和SP）配置碳配额，作为在市内具有很大影响力的国有企业QM 和SP，它们之间存在竞合关系[19]。在碳配额配置过程中，QM 和SP 与生态环境局存在讨价还价情况[20]，即他们与生态环境局互动决策配置碳配额。生态环境局与双寡头制造商共同对相关参数进行合理调整。在供应链网络中，设定存在3 个备选供应商、双寡头制造商（QM 和SP）、3 个备选分销商和1 个销售商。销售商的产品需求量Demc服从正态分布（1 200,802）。各节点间单位运输成本T为3元/t·km，单位距离运输碳排放因子W为0.005 6kg/t·km。直接碳排放因子μm1和μm2均为0.82CO2/t原材料。同时，参照《2017年中国区域电网基准线排放因子》[21]，间接碳排放因子We为1.041 6tCO2/MWh。参考中国碳交易网公布的相关信息，设定碳交易价格P为40 元/t。碳配额配置函数A(1)中，初始碳配额E为1 000t；QM初始碳配额e1为600t，SP初始碳配额e2为400t；生态环境局配额控制总量π设为2 000t；污染承担指数ε设为0.35。配置函数A(2)中，根据某市的统计年鉴，确定经济贡献指数γ设为0.6；生态环境局基于经济贡献指数对碳配额的初始调整系数θ设为0.65。生态环境局最终碳配额调整系数ρ=0.5，生态环境局考虑双寡头制造商反馈的调整系数σ∈[0.2,0.5]。供应链网络节点设施相关参数见表1。各个节点之间距离的相关参数见表2。

表1 供应链网络节点设施相关参数

4.2 模型求解

为求解政企双层规划下考虑碳配额的供应链网络优化问题，设定需求不确定置信水平为0.6，则政企双层规划下考虑碳配额的供应链网络存在最优结构，Pareto最优解集中对应的领导粒子最优碳排放为4 095.03t，最优总成本为1 881 470.2 元，最优碳配额为925t，其中QM 分得637.5t，SP 分得287.5t。该点对应的备选设施开设结构见表3。同时，在开设的各个设施间，比较其成本和碳排放，得到各节点间物流量，见表4。

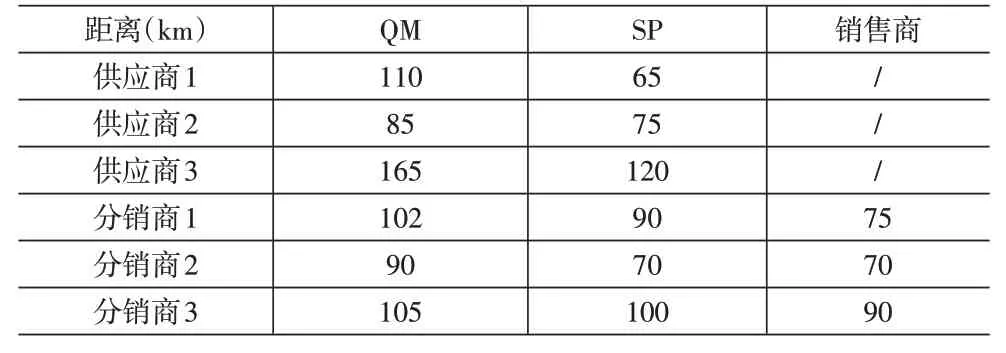
表2 各个备选节点之间的距离

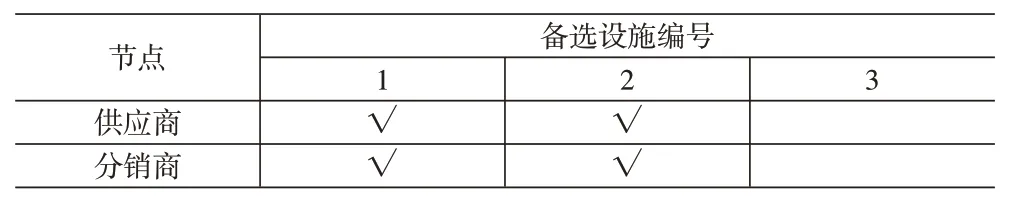
表3 备选设施开设情况

表4 已开设的各节点物流量分配

4.3 灵敏度分析

本文将探索最终碳配额和市场需求不确定置信水平变化对Pareto最优解集的影响。

（1）本文参考最优碳配额，以[700,1 000]t为碳配额配置区间为例，探索市场需求不确定置信水平为0.6 时，碳配额变化对供应链网络总成本和碳排放的影响。具体如图2所示。

①当碳配额在[700,800]t 区间时，供应链网络总成本和碳排放量均降低（Pareto 最优解集向左下移动），如图2 所示。由于生态环境局根据QM 和SP 反馈，并未对碳配额配置策略做出调整，上层规划模型中生态环境局考虑QM 和SP 反馈的调整系数σ很小，导致下层规划模型中最终碳配额A较小，碳交易收支Trad 较大，这时生态环境局的碳配额策略市场激励效果不明显，QM 和SP 虽然愿意参与碳交易，但动力不足，此时的碳配额策略收效甚微，供应链网络总成本和碳排放目标未达到最优。

②当碳配额在（800,900]t 区间时，供应链网络总成本和碳排放量持续降低（Pareto 最解集向左下移动）。这主要是生态环境局对QM 和SP 的反馈逐渐重视，上层规划模型中σ逐渐增大，下层规划模型中最终碳配额A增大，碳交易收支Trad减小，这时生态环境局碳配额的市场激励效果逐渐产生，QM和SP开始主动引导供应链其它企业参与碳交易，此时的碳配额策略初见成效，供应链网络总成本和碳排放呈现持续下降趋势，但仍未达到最优。

③当碳配额在（900,1 000]元/t区间时，供应链网络总成本和碳排放量不断降低（Pareto最优解集向左下移动）。随着生态环境局在初始碳配额的基础上充分考虑了QM 和SP 的反馈，上层规划模型配置碳配额效果达到最优。在这种情形下，QM和SP可以充分发挥链主企业的主导作用，积极引导其余供应链企业参与碳交易，同时也提升了供应链的整体竞争力。此时，通过合理分配设施选址及物流量，能够在供应链网络总成本和碳排放目标之间权衡求得Pareto最优解集。

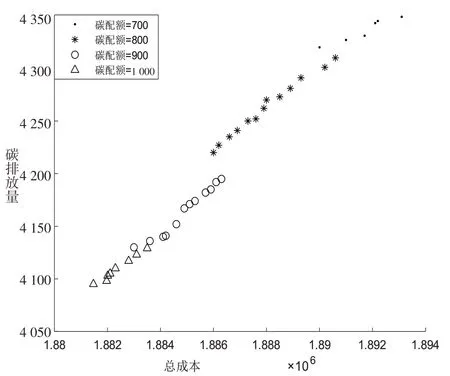
图2 碳配额[700,1 000]对Pareto最优解集的影响

（2）市场需求不确定置信水平α对Pareto最优解集的影响。本文以碳配额为925t分析市场需求不确定置信水平在0.3-0.9变动时对供应链网络总成本和碳排放的影响。

①随着置信水平α的不断上升，供应链网络选址位置及其规模也随之改变，见表5。市场需求不确定置信水平越高，需求量估算精度降低，设施节点间的流量相应增加。为满足供应链网络的持续运营，需要增设备选设施，以满足市场的产品需求。

表5 置信水平变化对应的选址策略

②随着市场需求不确定置信水平不断上升，供应链网络总成本和碳排放量均增大（Pareto最优解集向右上方移动），如图3 所示。需求不确定置信水平越高，需求量估算的精度降低。供应链网络的设施开设量和运输物流量都提高，因此供应链网络的碳排放量和总成本均有所提升。

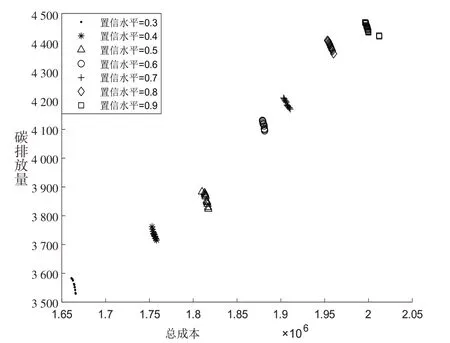
图3 置信水平[0.3,0.9]对Pareto最优解集的影响

5 结语

本文考虑政企双层互动决策，以生态环境局与双寡头制造商互动配置碳配额为例，验证政企互动配置碳配额的供应链网络优化模型的有效性，并得出以下几点结论：

（1）政企互动决策配置碳配额过程中，存在最优碳配额，且最优组合解集中的总成本和碳排放目标同向变化。政府部门应考虑双寡头制造商（QM 和SP）反馈合理配置碳配额。同时，双寡制造商反馈合理配置碳配额应该基于历史碳排放数据统计结果。在最终碳配额确定后主动引导其余供应链企业经营决策，使得它们减少不必要的间接排放，以达到总成本和碳排放最小化的目标，从而提升供应链的整体竞争力。

（2）供应链网络设施选址和Pareto最优解集均受市场需求不确定置信水平的影响。市场需求不确定置信水平升高，需求预测的精度降低，双寡头制造商扩产以满足市场需求，导致运输流量会相应增加。同时，为保证供应链网络的正常运营，需要增加供应链网络设施的开设，使得供应链网络总成本和碳排放均有所上升。因此，市场需求预测的准确性对供应链网络优化决策至关重要。双寡头制造商需综合参考一定周期内土地建设、交通运输、政府投资规划等相关数据，结合政府部门的碳配额策略，合理预测市场产品需求量。

政府部门仅对双寡头制造商配置碳配额，双寡头制造商需要承担相应的碳交易收支，这可能导致其它供应链企业的“搭便车”行为。同时，政府部门考虑双寡头制造商反馈的调整系数σ取值还比较主观，这些问题将在后续研究中进一步考虑。