基于粒子群算法的二次再热机组主蒸汽温度优化控制*
2021-02-07武海澄雷志伟阚俊超
李 达, 张 兴, 武海澄, 雷志伟, 阚俊超
(中国大唐集团科学技术研究院有限公司 华东电力试验研究院,合肥 230031)
0 引 言
二次再热机组是在一次再热机组的基础上,锅炉侧增加了二次再热系统,汽轮机侧增加了超高压缸[1]。其中,二次再热是指将汽轮机高压缸内做了部分功的蒸汽引出至锅炉二次再热器进行再次加热,然后引回汽轮机中低压缸继续做功。通过增加一个再热系统,可以提升2%~3%机组发电效率[2],同时相应减少了二氧化碳、氮氧化物等污染物的排放量,是我国火电机组未来重要发展趋势[3]。与此相应的是二次再热机组较一次再热在系统设计、工艺结构、运行参数等方面的差异较大,机组的响应偏慢,因此二次再热机组在主蒸汽温度的控制方面要比一次再热机组复杂得多[4]。
目前,通过调整喷水减温阀门的开度来控制主蒸汽温度是控制主蒸汽温度的主要方法,其控制算法采用串级PID控制。然而二次再热机组主蒸汽温度控制中,被控对象通常具有严重的非线性、滞后性、时变性等特点。同时热力系统中存在很多因素对主蒸汽温度造成影响,很难为主蒸汽温度建立准确的数学模型[5]。采用传统的串级PID控制,存在参数整定效果不佳、控制精度低、系统扰动大等不确定性因素,因此很难获得令人满意的动态响应特性。
将粒子群算法引入二次再热机组主汽温控制系统中,通过分析主蒸汽温度串级控制系统原理,建立控制对象传递函数,提出了基于粒子群算法的二次再热机组主汽温控制策略,并在仿真分析软件Matlab/Simulink上进行了验证。
1 控制对象特性分析
1.1 二次再热机组的基本原理
典型的二次再热机组热力系统如图1所示,二次再热机组比一次再热机组增加了一个超高压缸。蒸汽依次进入超高压缸、一次再热器、高压缸、二次再热器、中低压缸,最后进入凝汽器冷凝成水,再通过给水泵进入锅炉,形成汽水循环。
主蒸汽温度系统是一个多输入单输出对象,主蒸汽温度主要受3个因素影响:蒸汽流量、烟气热量和减温水流量[6]。其中通过改变减温水流量来控制主蒸汽温度,通常将过热器分为导前区和惰性区,该调节方式调节灵敏且精密。针对如图1所示的三级过热器而言,θ1为导前区温度测点,其传递函数为G1(s);θ2为惰性区温度测点,其传递函数为G2(s)。
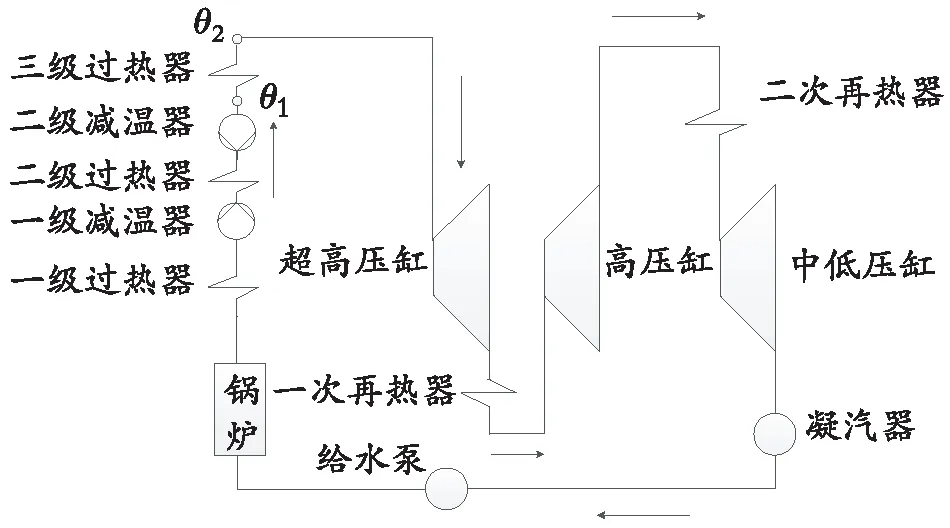
图1 二次再热机组热力系统示意图Fig. 1 Schematic diagram of thermal system of secondary reheating unit
1.2 主蒸汽温度PID串级控制
当采用喷水减温控制主蒸汽温度(即三级过热器出口蒸汽温度)θ2时,由于被控对象的迟延和惯性较大以及机组运行中对主蒸汽温度控制偏差也有一定的要求,因此采用单回路控制系统通常不能获得理想的控制品质[7]。针对主蒸汽温度控制通道的惯性迟延较大以及调节变量响应慢的特点,应在对象的控制通道中找出一个比调节变量响应快的中间物理参数作为控制目标的副参数,再通过串级控制系统来提高主蒸汽温度控制精度。蒸汽温度θ1和θ2的变化趋势是一致的,而蒸汽温度θ1的响应速度明显快于蒸汽温度θ2,因此在本控制方案中选取三级过热器入口处汽温θ1作为串级控制系统的副参数。
如图2所示,只要蒸汽温度θ1发生变化,副调节器PID2就会通过调整减温水调节阀的开度来改变减温水量,初步维持三级过热器入口处的汽温,对三级过热器出口主汽温作粗调作用。三级过热器出口汽温由主调节器PID1控制,只要三级过热器出口汽温偏离设定值θ,主调节器PID1的输出就会连续变化,使副调节器不断地去改变减温水量,直到主汽温恢复至设定值为止[8]。
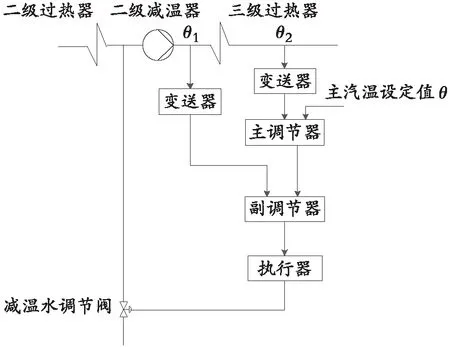
图2 主蒸汽温度串级控制系统Fig. 2 Main steam temperature cascade control system
主蒸汽温度串级控制系统原理如图3所示。其副回路是由对象的导前区G1(s)、导前温度变送器、副调节器、执行器与减温水阀门组成;主回路是由对象的惰性区G2(s)、主蒸汽温度变送器、主调节器及副回路组成。
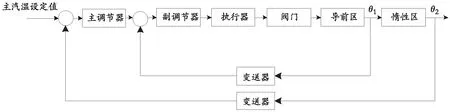
图3 主蒸汽温度串级控制系统原理框图Fig. 3 Block diagram of main steam temperature cascade control system
2 优化控制系统设计
2.1 粒子群算法原理
粒子群优化算法(PSO)是一种基于群体协作的随机搜索算法,它是模仿鸟类觅食行为而研发的一种算法[9]。粒子群中的每个粒子代表着该问题的可能解决方案,通过单个粒子的简单行为以及群体内的信息交互实现问题求解的智能性[10]。
粒子群算法通过迭代搜寻到一组随机粒子中的最优解,在第t次迭代时粒子i的位置用xi表示,它的速度用vi表示,每一次迭代时,粒子都会追寻两个极致来找到自己的方向和速率[11]。自己搜寻到的最优解称为个体极值pbest,整个群体追逐到的最优解称为全局极值gbest,在下一次迭代时粒子根据如下的公式来更新自己的速度和位置:
其中,d是正整数,w称为惯性因子,c1、c2为学习因子,rand()在0和1之间,k为更迭的次数。
2.2 二次再热蒸汽温度控制系统设计
2.2.1 适应度函数选取
选取绝对误差时间积分(Integral Time Absolute Error,ITAE)指标作为PID控制器的性能评价指标,即
其中,Jmin越小代表系统性能越好;e(t)为输出与输入之间的误差;t为时间。
2.2.2 基于PSO的串级PID控制器分析
图4为基于PSO的PID控制器系统结构图。
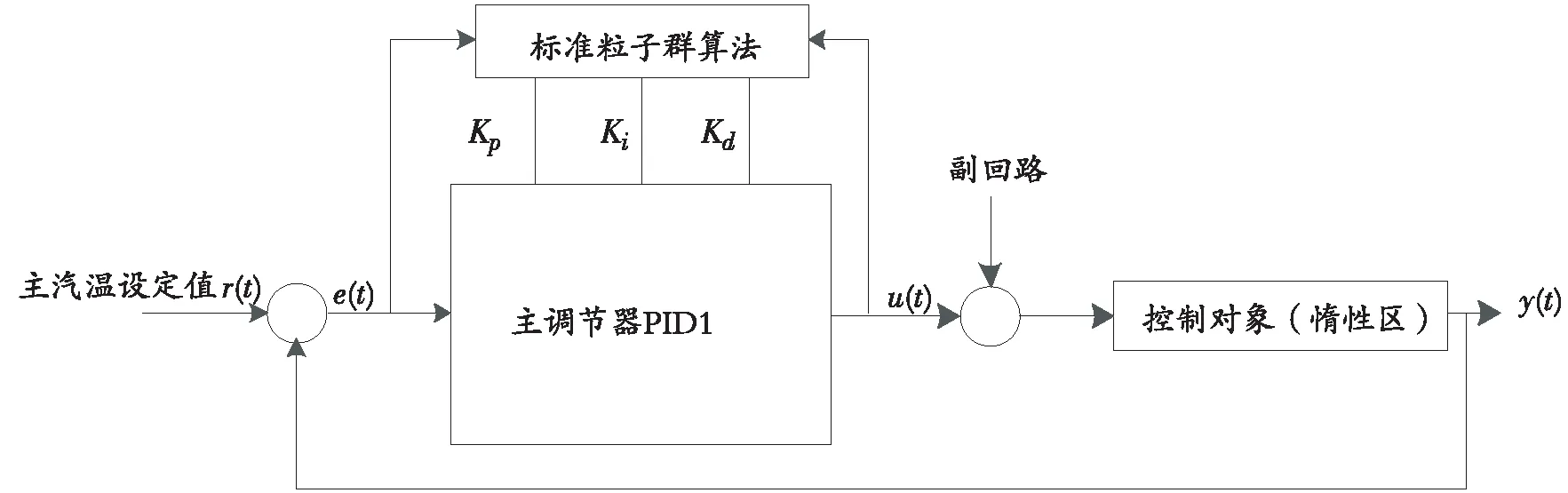
图4 基于PSO的PID控制器系统结构图Fig. 4 Structure diagram of PID controller system based on PSO
其中,r(t)即为主汽温设定值,经过主调节器PID1计算,再经过副回路后作用惰性区控制对象,其中将副回路看作是主回路的扰动,基于粒子群算法的控制优化仅针对惰性区的控制对象而言。
典型的PID控制器一般形式可表示为
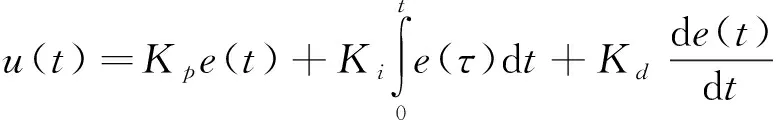
其中,r(t)、u(t)和y(t)分别为输入、控制器输出以及系统输出;Kp、Ki和Kd分别为比例、积分和微分系数。
在控制系统设计和仿真中,也经常写成传递函数形式:
其中,Ti为积分时间常数,Td为微分时间常数。
3 仿真验证
通过仿真实验对所提方法进行测试,在仿真分析软件Matlab上编写PSO算法程序,同时在Simulink系统中搭建PID模型文件。
采用文献[12]中的某1 000 MW超(超)临界二次再热机组的三级过热器汽温对象进行仿真试验,其中满负荷工况下,导前区G1(s)和惰性区G2(s)的传递函数如表1所示。本次被控对象即为G2(s)。

表1 某1 000 MW机组满负荷工况下主汽温对象传递函数Table 1 Object transfer function of main steam temperature for a 1 000 MW unit at full load
设定的标准粒子群算法的初始参数如下所示:粒子数pop为40;最大迭代次数为100;Kp、Ki、Kd3个参数的位置搜索范围为[0,100],速度范围为[-1,1];学习因子c1=c2=1.49;惯性权重从0.9到0.3线性下降。
针对惰性区G2(s)模型做阶跃响应实验,PID仿真模型如图5所示。输入信号为单位阶跃信号,设置的采样时间间隔为0.1 s。根据工业现场主汽温的控制特点,设置仿真时间为500 s。经过100次迭代后的单位阶跃响应图如图6所示。其中ZN方法是一种常见的PID参数整定方法,该方法是在阶跃响应的基础上,根据临界稳定性中的KP值来建立的。本次阶跃响应实验,将ZN方法作为对比方案进行控制性能分析。
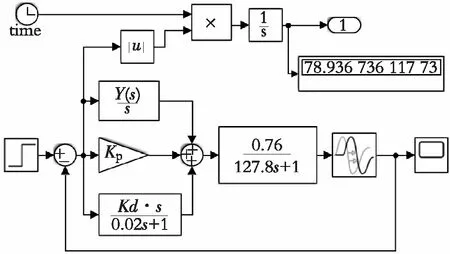
图5 PID仿真模型Fig. 5 PID simulation model
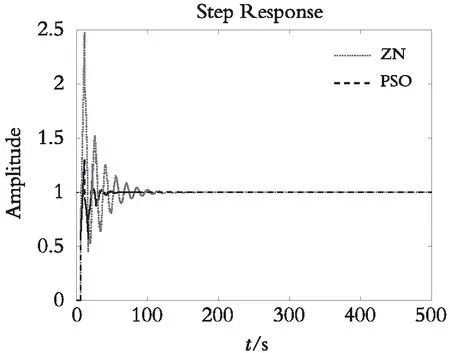
图6 单位阶跃曲线图Fig. 6 Unit step curve
表2为两种不同控制算法的Kp、Ki、Kd3个整定参数对比;表3为两种不同控制算法性能指标超调量、整定时间和ITAE(绝对误差)的比较。由图6和表2、表3可知,与ZN方法整定的控制效果相比较,基于PSO的优化控制方法得到的系统最大偏差最小,达到稳态值+2%的时间最短,系统的调节速度更快,控制性能最优。经粒子群算法优化之后,主调节回路的控制性能得到明显提高,系统输出在产生第一次震荡后立即减小并趋于稳定,稳定时间在 60 s 左右。

表2 不同算法的PID参数对比Table 2 Comparison of PID parameters of different algorithms

表3 不同算法的PID控制性能对比Table 3 Comparison of PID control performance of different algorithms
4 结束语
针对超(超)临界二次再热机组主蒸汽温度的大惯性、大迟延和强扰动等特点,提出了基于粒子群算法整定的主蒸汽温度优化控制方法。与传统的主汽温PID串级控制方法相比,优化后的控制方法不仅保留了串级控制系统抗内扰能力强的优点,而且有效地解决了系统稳定性和控制精度问题,增强了系统对不确定因素的适应性。通过阶跃响应实验表明,该控制方法对大惯性、大滞后的热工控制对象作用平稳,超调小。同时粒子群算法较为成熟,易于工程实现。因此,该方法为二次再热机组主蒸汽温度控制提供了一种有效的控制方法,具有指导工程实际应用价值。
