灌注桩高应变二种测力方法的差异性研究

2021-02-06郑文贞

广东建材 2021年1期

郑文贞

（广东省建筑科学研究院集团股份有限公司）

0 引言

近年来，随着设计不断优化以及施工工艺的长足进步，高层建筑物的基础中使用了越来越多的大直径、高承载力的混凝土灌注桩，桩的施工质量好坏直接关系着建筑物的整体质量，因此，准确的检测大直径灌注桩的竖向抗压承载力是否满足设计要求变得尤为重要。

目前，国内主要的基桩检测规范允许用静载和高应变法检测桩的竖向抗压承载力，就高应变法而言，在预应力管桩中的应用已经很成熟，但在混凝土灌注桩尤其在大直径、高承载力的桩型中应用相对较少。高应变法的信号采集包括力信号和加速度信号的采集，广东省标准DBJ/T15-60－2019《建筑地基基础检测规范》对力信号的采集给出了两种方式：在桩顶附近安装应变传感器或者在重锤上安装加速度传感器，后文分别称为应变测力和锤上测力。目前大多数检测机构倾向于采用应变测力，然而，实际情况是，对于大直径、高承载力的混凝土灌注桩，受混凝土的不均匀性、非线性以及测试环境等因素影响，在高锤击力的作用下，易造成桩顶两侧混凝土变形不协调和塑性变形过大，此时采用应变测力易出现两侧力信号峰值差距大、力曲线与速度曲线峰值比例失调、力信号失真等问题。因此，在大直径混凝土灌注桩中采用应变测力往往难采集到高质量的信号，影响测试结果。

为降低上述影响，应变测力测试前需预制混凝土桩帽作为替打，桩帽混凝土标号一般高出桩身混凝土标号两个等级，若选用大吨位重锤，则需进一步提高桩帽混凝土标号，根据桩的设计承载力以及满足“重锤低击”的原则，大多数灌注桩检测选用的锤重在100kN 至300kN的范围内，对于桩径小、桩长短的灌注桩，尚能与桩阻抗匹配，充分激发桩土相对位移，但是对于桩径大、桩长长的桩型，该锤重下提供的冲击能量往往不足，为此，高应变重锤的设计质量越来越大，据悉，目前国内用于检测灌注桩承载力的高应变重锤已达600kN，可想而知，其产生的高锤击力将会放大上述影响，增加采集高质量信号的难度。如图1，在高锤击力作用下，应变传感器测得的力信号失真。

图1 高锤击力下力信号失真

考虑到应变测力的上述局限性，有检测机构已用锤上测力采集力信号，关于锤上测力的有效性和准确性已有不少学者进行了相关研究，如：陈久照等[1]采用数值模拟方法分析了锤上测力的合理性、可行性和优越性,明确了该方法与应变测力产生差异的情形、原因以及对检测结果的影响程度。郭宝园[2]从理论上分析了锤上测力方法的准确性，并结合实际工程证明了采用锤上测力对大直径灌注桩进行高应变试验是可靠的。郑建民等[3]通过比较应变测力和锤上测力，证实了锤上测力的优越性，并通过动静对比试验，进一步验证了锤上测力的准确性。

本文以锤上测力为参照对象，结合已有的相关研究成果，分析造成应变测力在大直径灌注桩中应用局限性的根本原因，并通过实测数据证实分析结果，所得结论以指导灌注桩高应变法现场测试，进一步提升高应变法在大直径灌注桩中的应用。

1 两种测力方法的基本原理

1.1 锤上测力

广东省标准DBJ/T15-60－2019《建筑地基基础检测规范》规定在自由落锤锤体0.5Hr 处（Hr 为锤体高度）对称安装加速度传感器直接测量锤击力，测量基本原理为当重锤对桩顶施加竖向冲击荷载时，桩顶受到的作用力与重锤底面受到的反作用力大小相等、方向相反，故可认为桩顶附近传感器安装位置受到重锤的锤击力与重锤受到桩顶施加的反作用力相等，由此可计算出重锤对桩顶施加的锤击力［4］。

式中：F 为锤击力，m 为锤体质量，a 为实测加速度值。

1.2 应变测力

规范规定传感器宜分别对称安装在距桩顶不小于2d 的桩侧表面处（d 为试桩的直径或边宽），大直径灌注桩传感器安装位置与桩顶之间的距离可适当减小，但不得小于1d，锤击力计算公式如下：

式中：F 为锤击力，A 为测点处桩截面积，E 为桩材料弹性模量，ρ 为桩材料密度，c 为桩身波速，ε 为实测应变值。

由公式（2）、（3）可知，桩身波速c 和实测应变值ε直接影响锤击力计算值。

2 应变测力局限性分析

2.1弹性体假定对波速c 的影响

在桩中分析波的传播规律时，前提假设介质为弹性的，上述波速c 为弹性波波速，但是，混凝土毕竟不是理想弹性体，对于声波透射法和低应变法来说，由于应变量级较小，混凝土的变形在弹性范围内，尚可认为混凝土为弹性材料，然而对于高应变法来说，其产生的应变量级较低应变法或是声波透射法要高得多，尤其当重锤提供的锤击力较大时，此时混凝土的塑性特性就不得不考虑。当混凝土表现出弹塑性时，桩中产生的应力波并不是我们假定的弹性应力波而是弹塑性应力波，此时，波速实则为弹塑性波波速c′，其传播规律和特性大致为：混凝土变形初期，弹性波以一定的波速传播，随着混凝土变形增大出现塑性变形，塑性波也开始在桩中传播，塑性波的传播速度小于弹性波的传播速度，且塑性波波速随着应力的增大而减小。换句话说，混凝土表现出塑性变形越大，桩身波速则越低，从高应变法波速低于低应变法波速也证实了这点。因此，根据公式（3）计算得到的弹性模量较实际值要小，进而导致计算得到的锤击力值较实际值低。总结来说，在不考虑其他因素影响下，随着锤击能量增加，应变测力测得的锤击力值将越来越小于实际值。

2.2 实测应变值的影响

实测应变值容易受到偏心荷载、桩径及传感器的安装环境、混凝土的特性和质量等因素的影响。

⑴偏心荷载影响：重锤产生的冲击荷载可视为平面波，应变传感器测量的是间距约76mm 的两质点间的相对变形来反映力的大小，再通过平均两个测量力值得到桩身受力[2]。在偏心荷载作用下，应力波传至桩两侧应变传感器安装处两质点的时间差异造成两侧弹性变形不同，计算得到的应力时程曲线一致性差，虽然取平均值能降低偶然误差，但因测试数据少，仍无法较好的控制的误差，尤其在两个测试值相差较大时，如：当两侧力信号峰值相差一倍以上，任一个力信号与平均值之差的绝对值超过了平均值的33%。因此，规范中明确规定这种信号不能用于计算分析。然而，在实际工程中，不同程度的偏心情况经常发生，如图2。

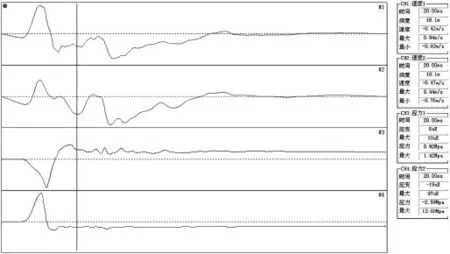
图2 偏心荷载作用下实测力信号

⑵桩径及传感器安装影响：基于圣维南原理，广东省标准DBJ/T15-60－2019《建筑地基基础检测规范》规定传感器安装位置宜距离桩顶不小于2d（d 为试桩的直径或边宽）以减小偏心荷载带来的影响，然而，在实际工程中，受现场条件、冲击设备及试验安全的限制，大多数大直径灌注桩测试中只能勉强满足距离1d 的要求，并且桩径越大桩顶的三维效应越明显，偏心荷载的影响越严重，实测信号效果越差，试验证明，当桩径较大或应变传感器安装位置距桩顶距离较小时，实测力信号可能会出现拉力，在测试中这种信号无效[2]。

⑶混凝土不均匀性和非线性的影响：不均匀性的影响表现在容易造成力信号失真，非线性的影响则表现为：随着应变增大出现塑性变形，使得实测应变值偏大且力信号曲线尾部不归零。

2.3 应变率对混凝土动弹性模量影响

按应变测力公式（2）计算锤击力大小，前提假设是混凝土满足胡克定律，但混凝土并非理想的线弹性材料，且高应变锤击力的实质是一种动荷载，根据混凝土的动荷载特性可知，在一定范围内，随着重锤落距增加，桩顶混凝土应变率随之增加，混凝土的弹性模量表现为动态增大，不同应变率对混凝土力学特性的影响已有很多学者做了较为全面的研究。如：Bischoff 等研究了高应变率下混凝土的抗压性能，试验数据离散性较大，但总体反应了混凝土的增强效应。雷光宇［5］等结合数值试验指出随着应变率的增大混凝土强度不断变大。邢峻伟［6］等研究了C20 混凝土弹性模量与应变速率的关系，得到了在混凝土弹性变形阶段，混凝土弹性模量随着应变速率增加而增加。孙吉书［7］等通过试验得出了C50 混凝土在一定的应变速率范围内，随着的应变速率增大，混凝土弹性模量明显提高。

然而，按公式（3）计算混凝土弹性模量，未表达出动态增大的特性，因此，随着重锤落距增加，使得计算得到的锤击力值将越来越小于实际锤击力值。

2.4 小结

上文论述了应变测力应用于大直径灌注桩时难以准确的测试锤击力，一方面受外界条件的影响，另一方面由于理论假设前提与实际情况的差异造成，由于影响因素很多，本文暂无法进行相关性和量化分析。但是，由上文论述可知，在理想的测试效果下，随着重锤落距增加，应变测力测得的锤击力值将越来越小于实际力值，进而可能造成实测力曲线与速度曲线峰值比例失调，影响高应变法的准确性。