轮式移动机器人预定时间轨迹跟踪控制

郜冬林，裴以建，朱久德，许文慧，刘云凯

(云南大学 信息学院，云南 昆明 650500)

近年来，机器人的研究快速发展，轮式机器人在社会生活中应用的越来越广泛，如家庭服务、安保巡逻、无人快递等. 非完整系统的控制问题因具有理论挑战性和广泛的使用性吸引了大批研究者.在文献[1]中，作者通过设计自适应控制器来实现非完整轮式机器人的轨迹跟踪. Wang等[2]通过基于测量的方法控制非完整移动机器人的避障.Zhang和Chu等[3-4]设计了可使非完整系统固定时间稳定的控制律. 轮式机器人作为典型的非完整系统，其轨迹跟踪问题是吸引众多研究者的热点方向. Luan等[5]提出的轨迹跟踪算法可应用于存在随机网络时延情况下的轨迹跟踪控制. 存在多领导的情况时，Jin等[6]提出的算法可使二阶多智能体系统存在扰动时实现轨迹跟踪，Hu等[7]设计的自适应控制器可实现在有向通信拓扑下的轨迹跟踪.

文献[8]提出的控制律可使误差渐近稳定，即当时间趋向于无穷时，误差收敛到零,因为误差收敛时间过长，所以很难应用到实际中. 文献[9]提出的控制律可使误差在有限时间内收敛到零，误差的收敛时间与其初始值有关，当初始值很大时，该控制律效果很差. 文献[4]提出的控制律使得误差系统成为固定时间稳定的系统，文中只能给出误差收敛时间的上界，无法给出确切的误差收敛时间，在对误差收敛时间有严格要求的应用中，使用该控制律无法得到很好的效果.

得益于有限时间控制技术的快速发展[10]，一些预定时间控制方法被提了出来. 文献[11]的控制方法可以较为方便地计算出误差的收敛时间，但是计算出的理论收敛时间远大于误差的实际收敛时间. 文献[12]给出的方法虽然可以得到精确的收敛时间，但是该控制方法只能应用于二阶链式系统，不能应用到受非完整约束的系统. 本文利用预定时间控制技术，结合轮式移动机器人的运动学特性，提出了可使受到非完整约束的轮式移动机器人与参考信号之间的跟踪误差在预定时间收敛的控制律，弥补了上述文献中所提控制律的不足，并利用Matlab仿真验证了本文提出控制律的有效性.

1 预备知识及问题描述

图 1 非完整轮式机器人Fig. 1 Nonholonomic wheeled mobile robot

受非完整约束的轮式移动机器人模型如图1所示，机器人的中心位于连接两后轮的车轴的中心，前轮位于垂直于后轴且相交于后轴中点的直线上.机器人在全局坐标系中的坐标为P= [x,y,θ]T，(x,y)为机器人中心在全局坐标系中的坐标，θ为机器人前进方向与X轴之间的夹角.

机器人的运动学模型可由下列微分方程描述：

其中，v、ω分别为机器人的线速度和角速度.

机器人受到的非完整约束的条件为y˙cosθ−x˙sinθ=0，即车轮与水平地面之间只有纯滚动，无滑动.

定义 1：全局有限时间稳定[13]非线性系统

x∈Rn是系统的状态， φ ∈Rp是系统的参数，f:R≥0×Rn→Rn为非线性函数，使得f(t, 0;φ)=0，即x=0为系统（2）的平衡点，t0∈ R≥0为系统的初始时刻，×指集合的笛卡尔积. 如果系统（2）的原点为全局渐近稳定且系统（2）的任意一个解x(t,t0,x0) 都在有限时间内收敛到原点，即当t≥t0+T(t0,x0),x(t,t0,x0)=0，T:R≥0×R →R≥0为稳定时间函数，则称系统（2）为全局有限时间稳定的系统.

定义2：固定时间稳定[13]如果系统（2）的原点是全局有限时间稳定的，且稳定时间函数是有界的，即 ∀x0∈Rn,t0∈R≥0,∃Tmax＞0, 使得T(t0,x0)≤Tmax，称系统（2）为固定时间稳定的系统.

定义3：预定时间稳定[14]如果系统（2）是固定时间稳定的系统，系统的稳定时间Tp和系统参数及初始条件无关且可由用户提前设定，则系统（2）称之为预定时间稳定的系统. 机器人预定时间轨迹跟踪问题即设计合适的控制律u= [v,ω]T，使得机器人在预先设定好的时间T跟踪上由参考位姿Pr=[xr,yr,θr]T和参考输入ur= [vr,ωr]T所描述的模型的轨迹，参考轨迹与机器人运动轨迹如图2所示.

图 2 参考姿态与机器人姿态Fig. 2 Reference posture and robot posture

定义跟踪误差为Xe=xr−x，Ye=yr−y， θe= θr−θ. 对跟踪误差进行坐标变换[15]：

对（3）式求导可得到误差系统模型为

可将误差系统看作是由一个二阶子系统（4）、（5）和一阶子系统（6）构成.

2 控制器设计

引理 1[14]对非线性系统（2），令D⊂ Rn为一个包含平衡点x= 0 的定义域. ψ1(x) 和 ψ2(x) 为定义在D上的两个连续正定函数. 如若存在一个连续可微的实值函数V:I×D→R≥0，I=[t0,tf) 为有限时间区间，其中，t0为初始时刻，tf为收敛时刻，存在η≥ 1，使得

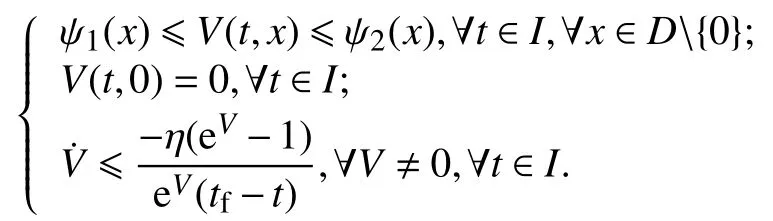
则系统的平衡点x=0是预定时间稳定的平衡点，且收敛时间T=tf−t0.

假设 1机器人可以完全获得参考信号的速度和角速度信号，且参考输入的角速度 ωr≠ 0.

假设 2参考信号的输入满足C2,C3≤ |ωr|≤C4.C1,C2,C3,C4均为大于零的已知常数.

由跟踪误差模型，可将机器人对轨迹的跟踪控制分两步设计：

第1步：设计机器人的角速度输入，使角度误差系统的状态 θe在t=tθ时收敛到零. 根据（6）式，tθ为角度误差收敛时刻，设计 ω 的控制律为

其中， α1≥ 1，tθ=t0+Tθ，Tθ为用户根据需求所设定的角度误差的收敛时间.

第2步：当t≥tθ时，此时 ω = ωr,θe=0，带入系统（4）、（5）可得

此时仅需考虑设计速度v即可. 设计v的控制律为

其中， φ (ye,t)= α2(eye−1)/[ωreye(tf−t)]， α2≥1， α3≥1，tf=tθ+Tf，tf为位置误差收敛时间Tf为 预定的位置误差收敛时间.

定理 1在假设1和假设2条件下，角度误差系统（6）在控制律（7）的作用下，将在预定时间tθ到达0，并在t＞tθ后，机器人与参考信号之间的角度始终一致.

证明将（7）式代入（6）式可得

即证明在t=tθ时， θe=0， 选择Lyapunov函数：证明完毕.

定理 2在假设1和假设2的条件下，应用控制律（10）可使机器人与参考信号之间的位置误差在预定时间tf到达0，且在t≥tf后，机器人与参考信号之间的位置始终一致.

证明利用反步法设计v[16]. 首先将xe看作（9）的输入，设计xe使得ye预设时间稳定. 令xe=并取Lyapunov函数V2(ye)=ye2，与证明定理1类似，可知ye将在预先给定的时间tf稳定到原点.

对（8）式设计v时，可先使xe稳定到原点，再追踪参考信号. 当tθ≤t＜tf时，令v=v1−v2，v1=vr+ωrye，带入（8）式可得

应用变量替换z=xe−φ(ye,t)，带入（8）、（9）式可得误差系统新表达式为

图 5 机器人运动轨迹Fig. 5 The trajectory of robot

3 仿真验证

在Matlab中对本文提出的控制律进行验证，取 α1=α2=α3=2，ωr=(t+1)/(t+2)，vr=3+sint，角 度 误 差 θe的 稳 定 时 间 为Tθ=2 s，位置误差(xe,ye) 的稳定时间Tf= 2 s，初始时间t0= 0，误差初始值 θe(0 )=2，xe(Tθ)=5，ye(Tθ)=2. 误差变化曲线分别如图3、图4所示. 机器人在平面上的运动轨迹如图5所示.

图 3 角度误差变化曲线Fig. 3 The curve of angle error

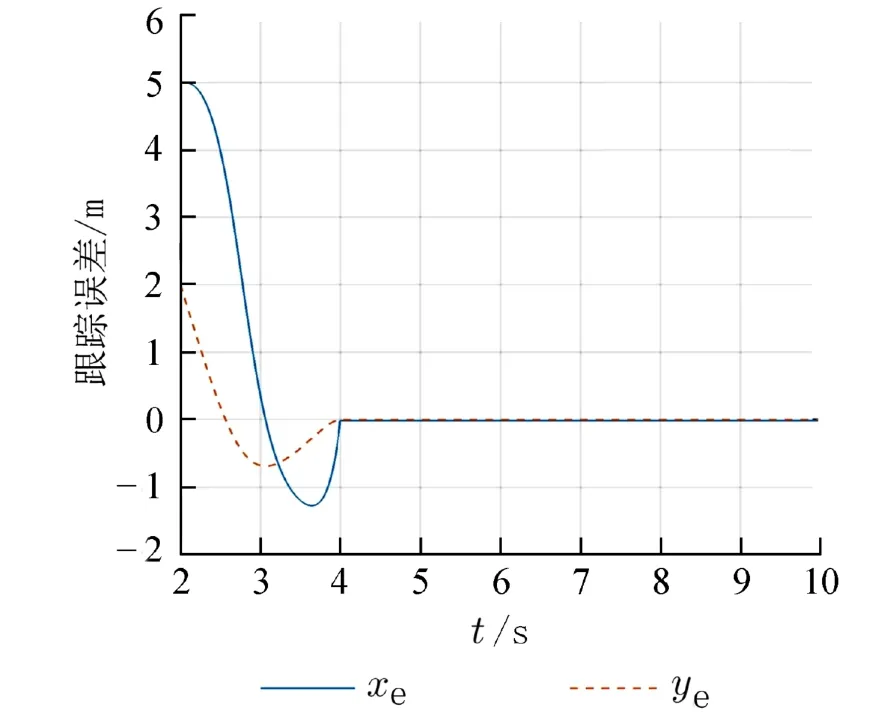
图 4 跟踪误差变化曲线Fig. 4 The curve of tracking error

由图3可看出在t= 2 s时，机器人和参考信号之间的角度误差收敛到零；在t＞ 2 s后，机器人和参考信号之间的角度误差始终为零. 角度误差收敛后，机器人开始追踪参考信号的轨迹，机器人位置与参考信号位置之间的误差变化曲线如图4所示，在t=Tθ+Tf=4 s时，轨迹误差收敛到零并在此之后始终保持为零. 由于位置误差系统为二阶系统且其必须在预定时间收敛到零，所以位置误差的收敛曲线不像角度误差一样由初始值直接收敛到零，会有一个超调量，但是超调部分远小于误差系统初始值,不会造成系统发散. 在角度误差和位置误差都收敛后，机器人的角速度和线速度也将与参考信号保持一致，由图5可看出，当机器人追踪上参考信号之后，机器人与参考信号的轨迹将始终重合，说明控制律（7）、（10）是有效的.

4 结论

本文通过应用预定时间收敛的控制方法，针对具有非完整约束的移动机器人设计了角速度和线速度的控制律，使得机器人在跟踪角速度不为零的目标时，跟踪误差的精确收敛时间可以根据实际情况提前设定. 现有的轨迹跟踪控制方法中，只能计算出误差收敛时间的上界，不能得到精确的误差收敛时间，本文提出的控制律可以直接提前设定收敛时间，因此提出的控制律相较于已有的控制律，可应用范围更广，仿真结果证明了该方法的有效性.在实际生活中，编队追踪的应用更加广泛，下一步会将预定时间轨迹跟踪控制方法结合多智能体控制，研究多机器人编队的预定时间轨迹跟踪.