基于磁极参数的表贴式永磁同步电机齿槽转矩研究*

洪 涛， 鲍晓华， 刘佶炜， 李仕豪

(合肥工业大学 电气工程与自动化学院，安徽 合肥 230009)

0 引 言

表贴式永磁同步电机(SPMSM)具有结构简单、效率高、转矩电流比高、功率因数高等优点，因此在现代工业领域已得到越来越广泛的应用。永磁体和开槽电枢铁心之间的相互作用不可避免地导致齿槽转矩[1]，从而导致转矩波动、振动和噪声，并影响系统的控制精度和运行稳定性。齿槽转矩是永磁电机的特殊问题之一，也是设计和制造高性能永磁电机时必须考虑并解决的关键问题。

对于SPMSM，气隙磁密接近矩形波，含有大量谐波分量，文献[2-3]通过改变永磁体的磁极参数优化气隙磁密波形来抑制齿槽转矩。文献[4]利用遗传算法(GA)优化永磁电机的形状以实现齿槽转矩最小化,并通过数值试验验证了该方法的有效性。文献[5]使用具有离散偏斜角的表面安装永磁体并基于GA优化程序来削弱齿槽转矩。文献[6-8]提出了极宽调制和极幅调制相结合的方法，采用宽度一致的分块永磁体和不同剩磁强度材料组合的方法，削弱了气隙磁密中的谐波。相似地，采用不同永磁材料相同永磁体厚度的组合磁极也可以减小气隙磁密中的谐波含量，Shen等[9-10]对此方法进行了大量的研究。通过改变永磁体形状等方法[11-13]来削弱齿槽转矩已获得了不错的成果，例如文献[14]对永磁体削极处理下的边缘厚度进行了分析和优化。文献[15]引入磁极加长系数改变极弧系数的分配比来削弱齿槽转矩。文献[16]采用不等厚分段式永磁体代替传统永磁体来削弱齿槽转矩并达到了预期效果。但是，这些结论大部分是通过模拟获得的，很少是通过分析和理论推导得出的。此外，这些文章大多数仅对单一结构进行参数分析，而没有比较多种结构对齿槽转矩的影响。

本文基于能量法和傅里叶分解，首先给出SPMSM齿槽转矩的解析分析方法，然后推导了不同永磁体模型下齿槽转矩公式，给出了相应的能有效削弱齿槽转矩的参数确定方法。以50 kW、8极和11 kW、16极2台SPMSM为样机，利用有限元方法验证上述方法的有效性，最后对削极与组合磁极的磁极参数进行优化，并分析对电机性能的影响。

1 齿槽转矩的解析分析方法与磁极模型分析

1.1 齿槽转矩产生机理

齿槽转矩是当永磁电机的绕组不励磁时, 由永磁体和铁心之间的相互作用产生的转矩。基于能量法，齿槽转矩可以表示为[17]

(1)

式中：W为不带电的电机磁场能量；α为定转子相对位置角。

存储在铁中的能量较小可以忽略不计，因此存储在电机中的磁场能量约等于存储在电机的气隙和永磁体中的磁场能量之和：

W≈Wgap+WPM=

(2)

式中：hm(θ)、σ(θ,α)、Br(θ)分别为永磁体的磁化方向长度、气隙的有效长度、永磁体沿周向剩磁的分布。

对于永磁体和槽均匀分布的SPMSM而言，通常可以通过傅里叶级数来扩展Br2(θ)和气隙相对磁导率的平方。对于通用永磁体模型，Brn和Gn的公式如下：

(3)

(4)

(5)

(6)

(7)

式中：Br为永磁体的剩磁；Brn为Br2(θ)的n次傅里叶展开系数；p为极对数；αp为极弧系数；Gn为气隙相对磁导率平方的n次傅里叶展开系数。

则齿槽转矩可以表示为[17-18]

(8)

式中：z为定子槽数；La为电枢铁心的轴向长度；μ0是真空的磁导率;R1为定子的内半径；R2为转子的外半径；n是使nz/(2p)为整数的整数。

1.2 磁极模型分析

由式(8)可以看出，削弱齿槽转矩可以通过改变Gn和Brn的幅值，这是对齿槽转矩起主要影响的。由式(2)～式(8)可以看出，齿槽转矩与气隙磁密沿着电枢表面的分布有关。永磁体的参数变化会直接影响气隙磁密在电枢表面的分布。式(3)～式(7)适用于普通磁极结构，如图1(a)所示。对于不同的永磁体模型，气隙磁密分布不同会导致齿槽转矩中Gn和Brn的解析式不同。因此，本文基于永磁体磁极参数对SPMSM的齿槽转矩进行研究，建立不同的磁极模型并进行解析推导。

图1为各磁极模型的示意图。其中，图1(a)为普通磁极，永磁体采用径向充磁方式。图1(b)为环形磁极，环形磁极采用正弦或者余弦充磁方式。由于函数充磁的复杂性和加工工艺的限制，采用多块极弧系数和厚度均相等、剩磁大小按照正弦调制的分块永磁体代替整体的永磁体，如图1(c)所示。图1(d)为组合磁极，将原始的单一永磁体材料更改为多种材料的组合，中间部分为主磁极，两端为辅助磁极。图1(e)为不等厚磁极。图1(f)为削极结构的永磁体，为了方便解析分析可以等效成模型图1(g)。

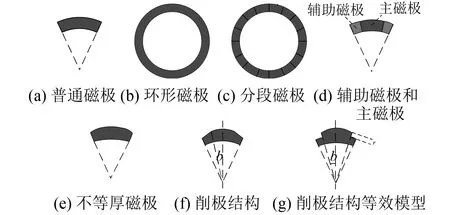
图1 磁极模型

磁极模型分类的流程图如图2所示。本文通过极弧系数对SPMSM进行分类，对于极弧系数为1的永磁体采用正弦充磁来调制气隙磁密波形从而达到削弱齿槽转矩的效果，由于工艺限制往往采用分段充磁的方式来代替正弦充磁。对于常见的极弧系数小于1的磁极结构，也可以采用正弦充磁的方式达到削弱效果，但工艺复杂、应用范围有限，因此现代工业大多采用组合磁极和削极结构来达到削弱齿槽转矩的效果。

图2 磁极模型分类

1.3 解析分析

对于图1(b)所示的环形永磁体，采用余弦函数充磁，如图3所示。此时αp= 1，Br(θ)的分布可表示为

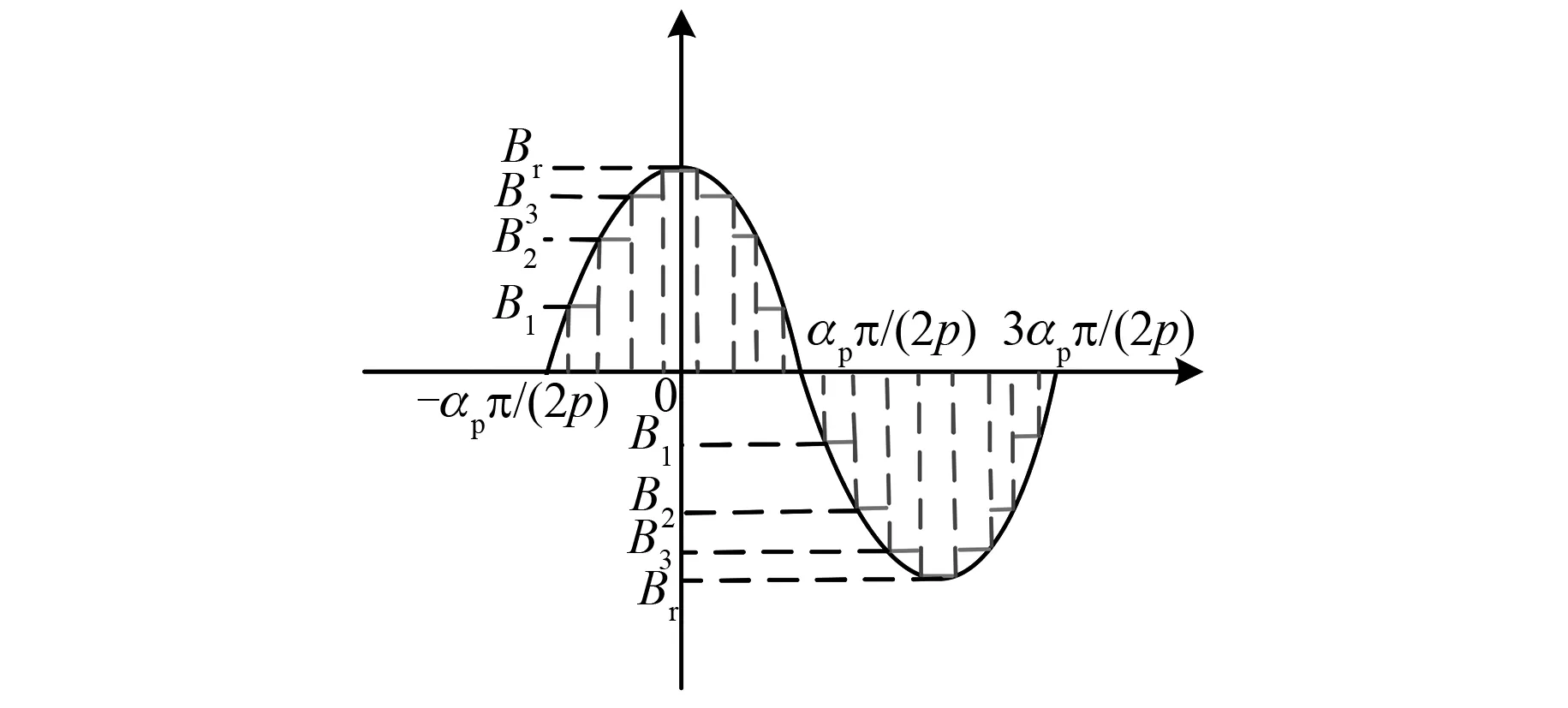
图3 环形和分段式永磁体Br(θ)的分布

Br(θ)=Brcos(pθ)

(9)

该模型下，仅Br(θ)的分布发生了变化，因此Gn的表达式不变，Brn发生变化，可表示为

(10)

图1(c)采用分段式永磁体，即采用分段的径向充磁的永磁体代替余弦充磁方式，此时Br(θ)的分布见图3。其解析式可表示为

Br(θ)=kiBr1,

(11)

式中：i为1～s范围内的正整数。

相似的，Gn的表达式不变，Brn发生了变化，此时的Brn可表示为

(12)

式中：ki是其他永磁体的剩磁Bi与剩磁Br的比值；Br1为分段中的最大剩磁；s为单极下永磁体的分段数。

图1(d)为组合磁极，其原始的单个永磁体材料更改为2种材料的组合。图4为组合磁极的Br(θ)的分布，可表示为

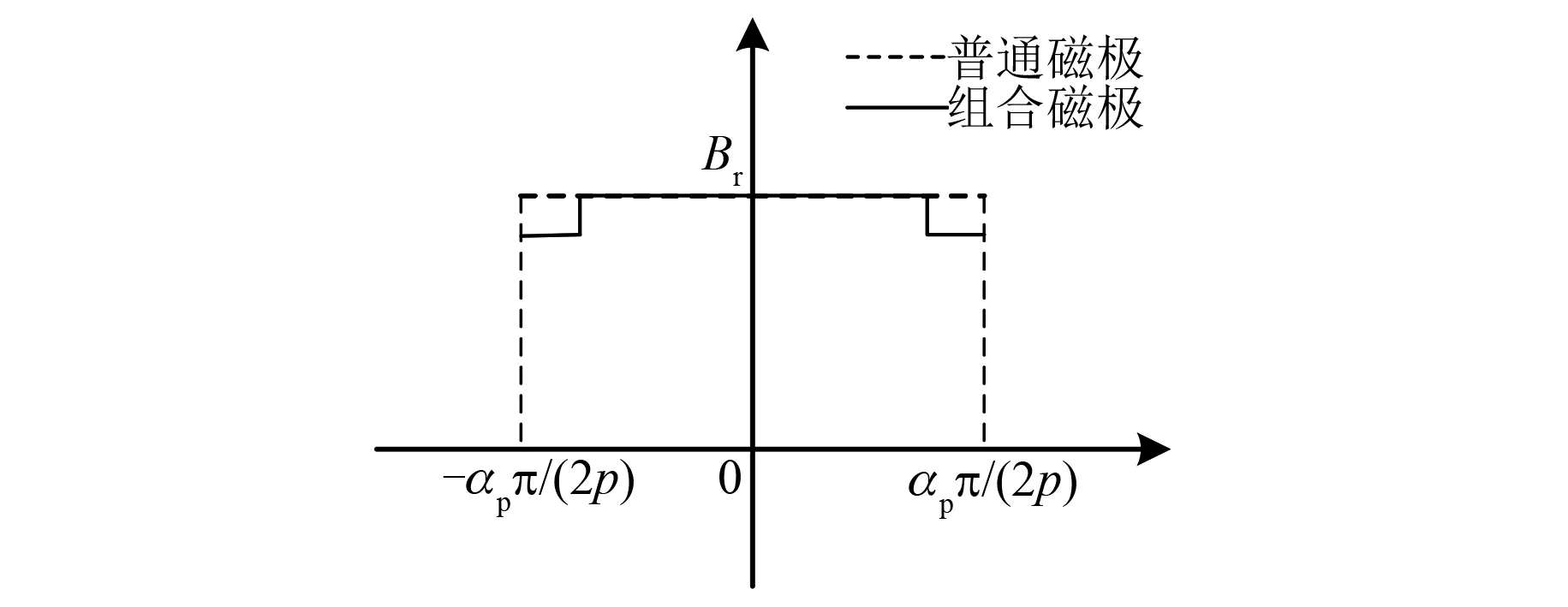
图4 组合磁极下的Br(θ)分布

Br(θ)=

(13)

式中：Br1为辅助磁极的剩磁；Br2为主磁极的剩磁；β为辅助磁极占总磁极的百分比。

此时，Gn的表达式不变，变化后的Brn可表示为

(14)

SPMSM气隙磁密沿着电枢表面的分布可以表示为

(15)

对于图1(e)的不等厚永磁体、图1(f)和图1(g)的削极结构来说，气隙磁密的分布如图5所示。气隙磁密的变化仅由气隙相对磁导率的变化，此时Brn表达式保持不变，而Gn的表达式相对于普通磁极模型各异。

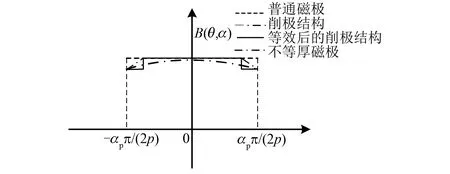
图5 不等厚永磁体和削极结构的B(θ,α)的分布

对于图1(e)不等厚永磁体，Gn的表达式为

(16)

由于目标函数的不确定性，很难得到具体的参数化分析结果。特殊的，采用图1(f)所示的削极结构来建立模型，此时Gn的表达式为

(17)

式(17)中，b如图1(f)所示。

此时气隙相对磁导率仍然是多变量函数。为了便于分析进一步简化模型，将模型等效为图1(g)所示的结构，则Gn的表达式为

(18)

式(18)中，b和r如图1(g)所示。

本文通过能量法推导了不同永磁体模型下的齿槽转矩公式，可以看出，通过永磁体参数来削弱齿槽转矩的方法实质上改变了Gn和Brn的幅度，且进一步对齿槽转矩的幅值产生影响。对于不同的永磁体模型，齿槽转矩解析公式中的Gn和Brn的表达式有所差异，而这些差异由永磁体的参数决定。与普通磁极[图1(a)]相比，环形磁极[图1(b)]、分段磁极[图1(c)]和组合磁极[图1(d)]中Gn保持不变，而Brn发生改变；而不等厚永磁体[图1(e)]和削极结构[图1(f)、图1(g)]下的Gn发生了变化，而Brn保持不变。通过解析公式可以看出，各个模型下的齿槽转矩受不同磁极参数的影响，其中环形磁极模型下齿槽转矩与剩磁相关，分段磁极模型下齿槽转矩与分段数s和剩磁比ki相关，组合磁极结构下的齿槽转矩与辅助磁极的剩磁幅值和辅助磁极所占的百分比有关，不等厚永磁体下齿槽转矩受到其永磁体表面分布的影响，削极结构下的齿槽转矩是关于削槽的深度和削槽的宽度的函数。

2 仿真分析

2.1 不同永磁体模型对齿槽转矩的影响

基于以上理论分析，可以看出不同的永磁体模型会影响电机的齿槽转矩。上述理论推导为有限元分析的参数选择提供了指导，通过有限元仿真可以得到磁极参数对齿槽转矩具有更直观的影响。因此，本文以1台50 kW、8极的SPMSM为例来验证不同磁极模型对齿槽转矩削弱的有效性，其有限元模型如图6所示，样机I的主要参数如表1所示。

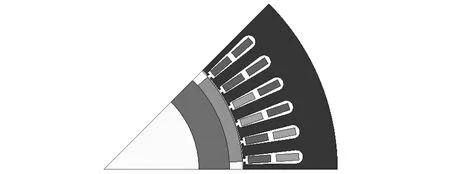
图6 样机I电机有限元模型

表1 样机I的主要参数

齿槽转矩在定子和转子的相对位置改变的齿距内是周期性的变化，且周期数取决于极槽配合。根据式(8)可以看出，周期数为使nz/(2p)为整数的最小整数n。极数和槽数的合理组合可以使周期数更长，周期数越长，齿槽转矩幅值越小。样机I整数槽电机，其齿槽转矩较大，会对电机的性能产生更大的影响。因此，由永磁体的参数化引起的齿槽转矩的减弱效果更加明显。本文在进行有限元仿真分析永磁体参数对齿槽转矩影响时，对多种永磁体模型进行了建模分析，包括分段磁极、组合磁极、不等厚磁极和削极结构。

图7为不同永磁体模型下的齿槽转矩波形图。可以看出，通过磁极参数改变得到的永磁体模型确实可以减小齿槽转矩幅值，但是对齿槽转矩的减弱程度是不同的。其中，削极结构、分段磁极和组合磁极的应用对齿槽转矩的削弱尤为显著。

图7 不同磁极模型下的齿槽转矩对比

分段磁极采用多块极弧系数和厚度均相等，剩磁按照正弦调制的永磁体组合而成，工艺复杂，应用并不广泛。相比之下，工业常用生产较为方便的组合磁极和削极结构来削弱齿槽转矩。因此，以11 kW、16极的低速大转矩电主轴SPMSM为例，对组合磁极和削极结构进行参数化研究。图8(a)为低速大转矩电主轴永磁电机的实物图。该电机有限元仿真模型如图9所示。样机II采用分数槽，其主要参数如表2所示。

图8 低速大转矩电主轴永磁电机实物模型

图9 普通磁极模型下的样机II有限元模型

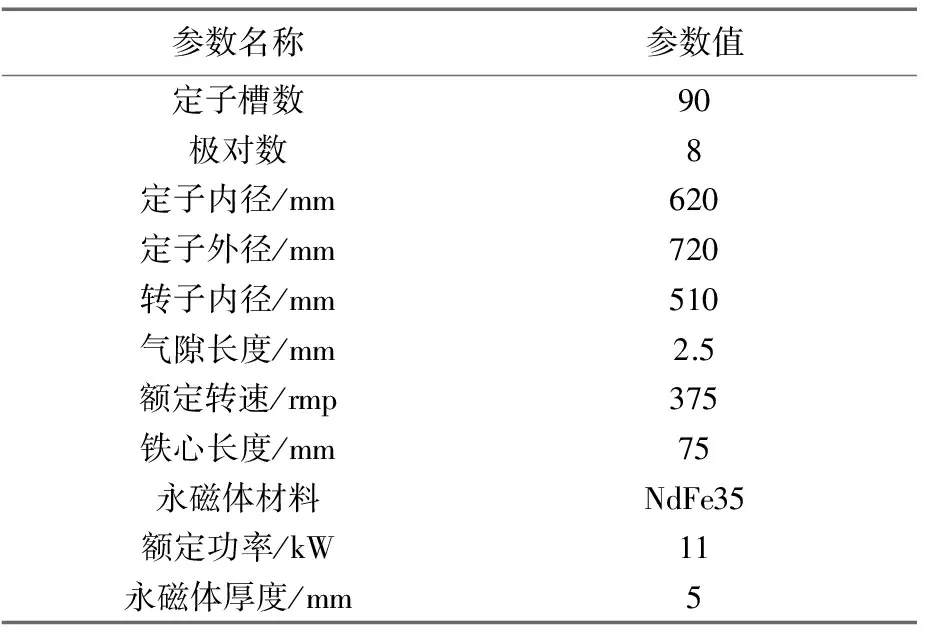
表2 样机II的主要参数

2.2 极化结构对齿槽转矩的影响

由式(8)和式(18)可以看出，削极结构通过改变削槽的深度和削槽的宽度来改变Gn的振幅，进而影响齿槽转矩。为了准确地分析削极结构对SPMSM齿槽转矩的影响，需要建立槽深和槽宽2个参数。

图10为削极结构的样机II局部二维模型图。

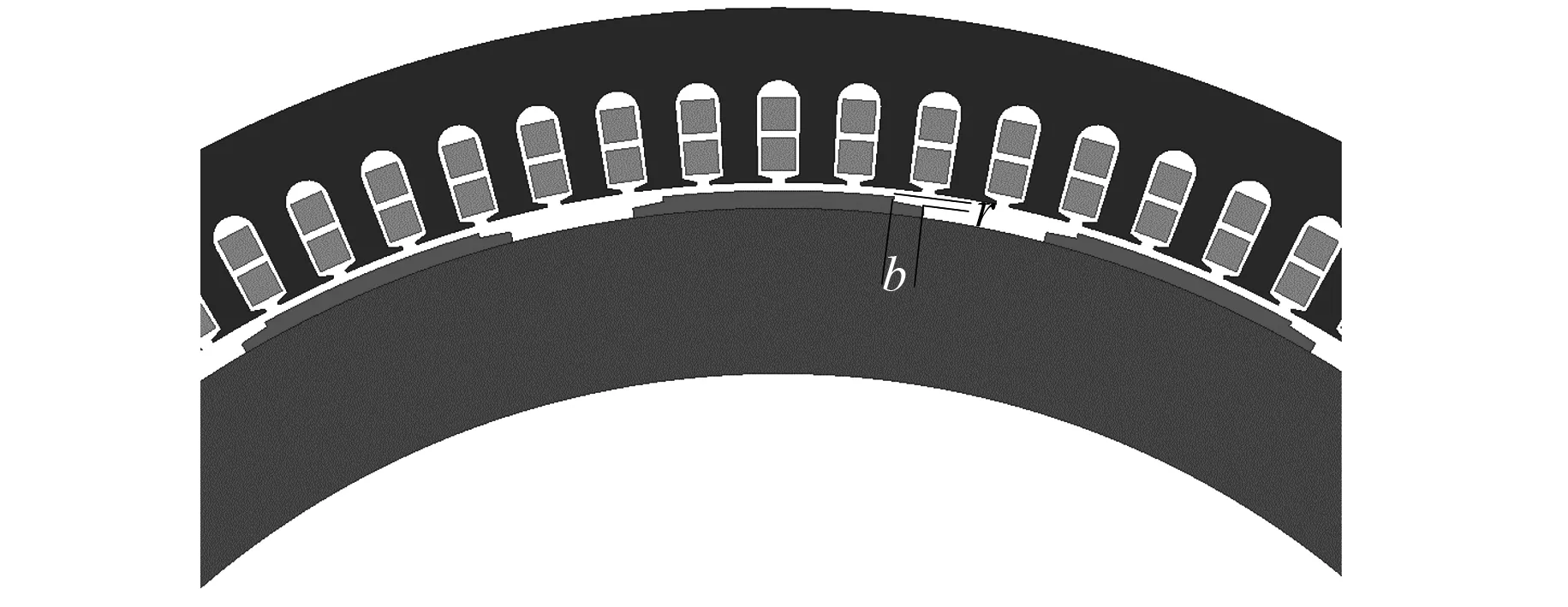
图10 削极结构的样机II的局部二维模型图

其中，标记了槽深r和槽宽b。与原始永磁体相比，削极结构的永磁体能量在一定程度上降低了，这可能导致气隙磁通密度的基波幅度减小。因此，选择适当的槽深和槽宽可以在确保电机性能的同时减弱齿槽转矩。

在研究极化结构对齿槽转矩的影响时，削槽深度r取值范围为1～4 mm(步长为1 mm)，削槽宽度b取值范围为5～30 mm(步长为5 mm)。采用有限元二维建模分析的方法仿真得到不同槽深和槽宽下齿槽转矩的最大值，如图11所示。

图11 不同槽深和槽宽下齿槽转最大值的3D表面图

从图11可以看出，槽深和槽宽对齿槽转矩有很大的影响，选取合适范围的槽深和槽宽可以有效地削弱齿槽转矩。有限元仿真获得的部分数据记录如表3所示。其中,Br是空载气隙磁通密度的径向分量基波幅值。

表3 有限元仿真数据

当槽深为2 mm，槽宽为20 mm时，齿槽转矩的峰值最小为0.229 N·m，仅相当于原始设计的36.4%，此时气隙磁密的基波幅值没有太大波动。此外,不合理的槽深和槽宽会增大齿槽转矩，还会引起气隙磁密度的畸变。

对于样机II，当槽深取永磁体厚度的0.4倍、槽宽取永磁体宽度的0.23倍时，齿槽转矩会显著降低，此时且气隙磁密度不会太大变动。削极结构已经在工业应用中用于降低齿槽转矩，见图8(b)。

2.3 组合磁极对齿槽转矩的影响

从式(8)和式(14)可以看出，组合磁极中的齿槽转矩受2个因素的影响：辅助磁极的剩磁幅值和辅助磁极所占的百分比。这2个参数会影响Brn的幅值，进而影响齿槽转矩的大小。图12为组合磁极结构SPMSM的局部二维模型图。

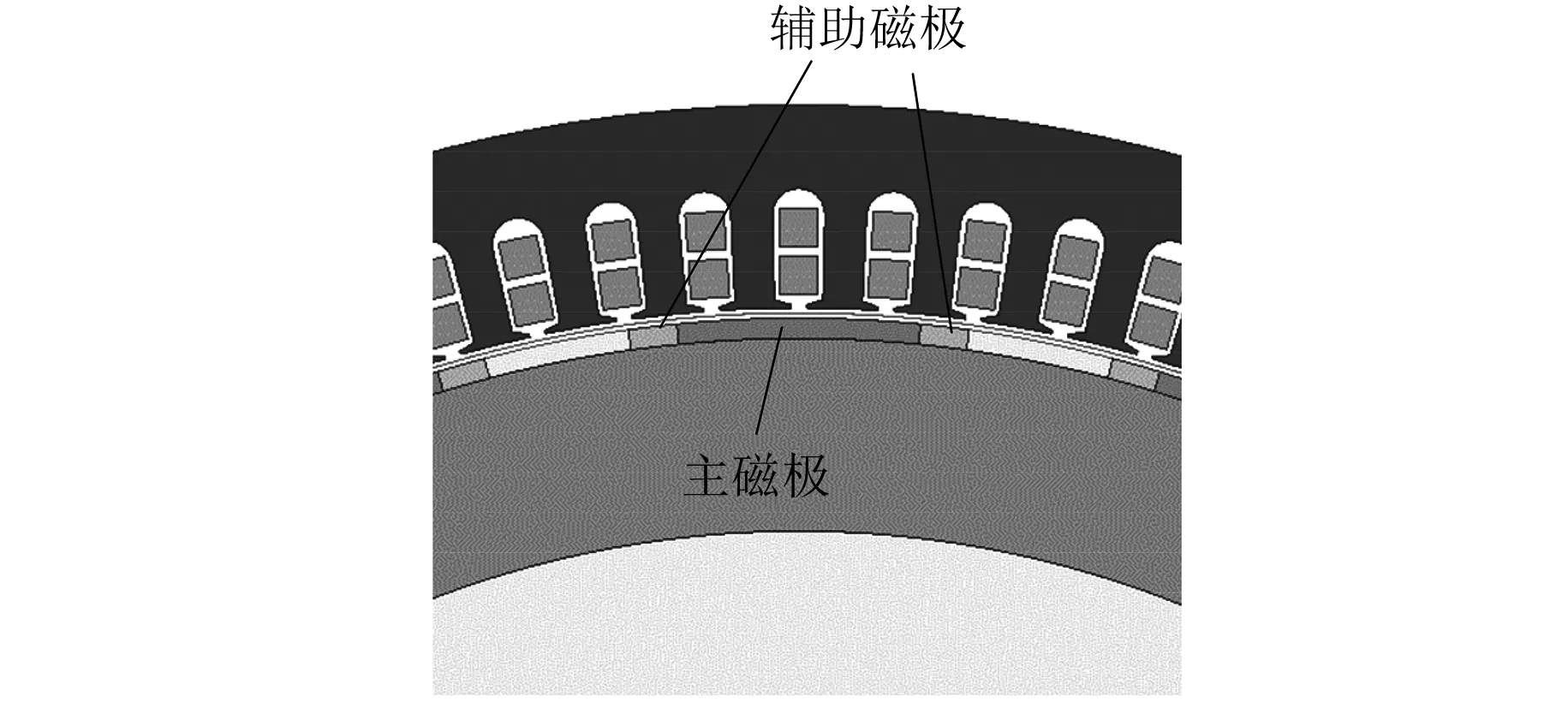
图12 组合磁极结构SPMSM的局部二维模型图

在研究组合磁极对SPMSM齿槽转矩的影响时，将β定义为辅助磁极所占的百分比，将s定义为辅助磁极与主磁极的剩磁之比。与主磁极相比，辅助极的剩磁小于主极，当使用组合磁极代替传统磁极时，永磁体的储能会一定程度削弱。因此，在选择辅助磁极和辅助磁极占比2个参数来减小齿槽转矩时，需要确保电机的性能。β的取值范围为1/7～4/7(步长为1/7)，s的取值范围为0.2～0.8(步长为0.2)。本文采用有限元二维建模分析的方法，绘制了不同β和s下齿槽转矩最大值的3D表面图，如图13所示。组合磁极下部分数据记录见表3。

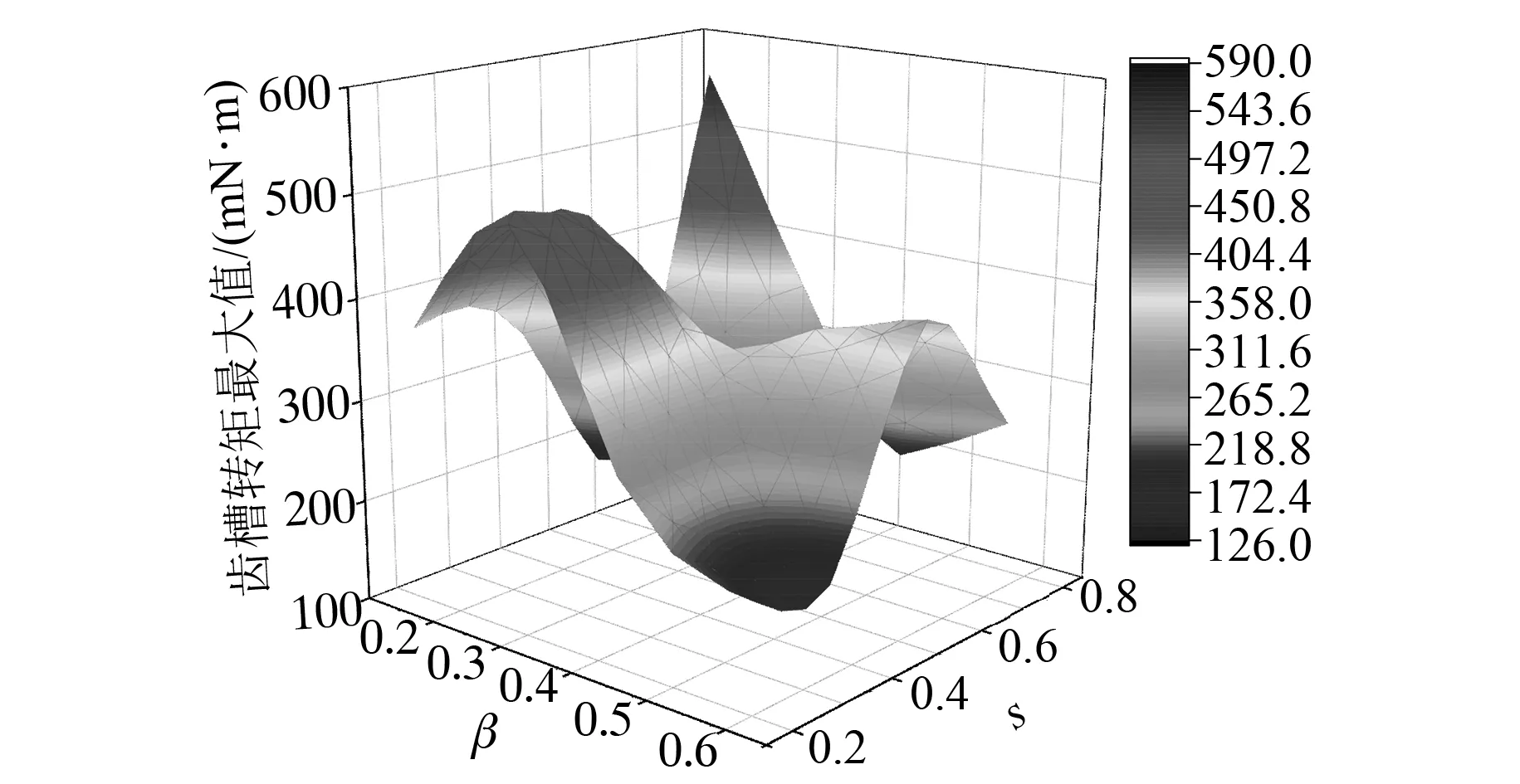
图13 不同β和s下齿槽转矩最大值的3D表面图

从图13可以看出，β和s对齿槽转矩影响较大，合适的β和s配比能有效削弱齿槽转矩，并确保气隙磁通密度不会太大波动。当β为1/7、s为0.6时，齿槽转矩仅为0.126 N·m，仅相当于原始设计的20%。从表3可以看出，此时气隙通量密度没有受到显着影响。当β为4/7、s为0.4时，齿槽转矩为0.147 N·m，但气隙磁通密度幅值显著降低。对于该样机，当β为1/7、s为0.6时，在确保气隙磁通密度时，齿槽转矩得到显著减弱。

2.4 削极结构和组合磁极对电机其他性能的影响

电机的磁极参数发生改变时，会对电机的性能产生影响。本文利用有限元对采用削极结构和组合磁极的样机模型进行分析。对比各模型下的电机性能，如表4所示。额定电流激励下的各磁极模型电机输出转矩曲线如图14所示。

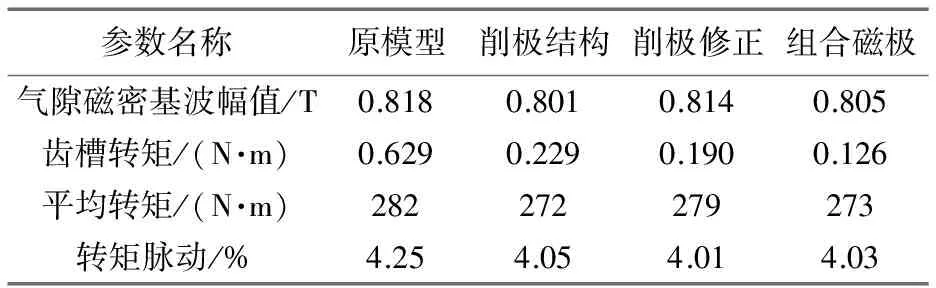
表4 各模型电机性能对比

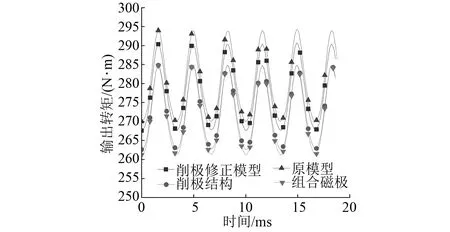
图14 电机输出转矩波形

从表4可以看出，采用本文的齿槽转矩削弱措施以后，电机的气隙磁密基波幅值、平均转矩、转矩脉动波动较小，不会对电机性能产生较大影响。

为了弥补由于削极结构、组合磁极等结构带来平均转矩、气隙磁密减少问题，可以采用磁极磁能不变的方法进行修正。本文对削极结构进行修正，将由于削极损失的永磁体均匀添加到永磁体厚度上，弥补磁能的削弱。从表4和图14可以看出，齿槽转矩被削弱的同时电机性能没有太大波动。

3 结 语

本文研究了不同磁极参数对SPMSM齿槽转矩的影响。基于能量法和傅里叶分解，推导了不同永磁体模型下的齿槽转矩公式。通过有限元仿真软件对不同永磁体模型下的齿槽转矩进行了仿真。然后对削弱效果显著的削极结构和组合磁极进行参数化分析，最后分析其对电机其他性能的影响。通过理论推导和有限元分析得出以下结论：对于不同的永磁体模型，齿槽转矩解析公式之间的差异在于Gn和Brn的差异，磁极参数的变化会影响Gn和Brn的幅值，进而影响齿槽转矩的大小。对于单一模型，合理的选择磁极参数可以在保证电机性能的情况下显著削弱齿槽转矩。