神经网络算法在函数逼近中的应用*

张 婷

(山西大学商务学院，山西 太原 030001)

0 引言

在工程应用中，有一些复杂问题需要解决时，我们经常会用简单的方法去替代它。在复杂计算中，也希望能有简单的函数来替代负载的函数，并且能够达到和复杂函数类似的效果，越类似称为误差越小。这种替代的方法称之为函数逼近，很多应用场合，比如人工智能，再比如图像处理等领域都会用到函数逼近算法。随着人工智能和计算机技术的发展，人工神经网络又迎来了它的春天。神经网络算法根据人体大脑结构的复杂神经元结构，进行层层传导而建立。依靠神经元和神经元之间的相互连接，实现信息的传递处理。神经网络算法应用广泛，比如生物领域、图像处理、信号处理、模式识别、人工智能等。随着其广泛应用，各种实现方法较多，比如python编程实现，MATLAB编程实现等，都能快速调用函数或者工具解决函数逼近问题。本文利用MATLAB工具箱，快速方便地实现了神经网络算法。神经网络和别的技术结合，比如小波分析、混沌神经网络、粗糙集理论、分形理论等，也是其发展方向。其中BP神经网络有较强的映射能力，主要用于函数逼近、函数压缩等。本文通过MATLAB仿真来分析BP网络在函数逼近中的应用。通过调节信号的频率、隐含节点的层数，分析它们对函数逼近的影响。

1 BP神经网络结构及学习

BP神经网络的信息传导主要是两个方向：一是正向传导，是指信号的传导，从输入到输出。另一方面是反向传导，是指误差的传播，方向从输出到输入。BP网络是一种前馈神经网络，由输入层、隐含层和输出层组成。图1所示的神经网络结构图，一共有3层。图中可以看出，只有相邻层的神经元之间会直接连接，同一层神经元节点之间没有连接[1]。神经元网络也可以包含多层隐含层。

图1 三层BP神经网络结构图

图1中，xj表示输入层的节点;Φ表示隐含层的激励函数;Ψ表示输出层的激励函数;wi,j表示隐含层到输出层的权值，其中i表示隐含层的节点位置，j表示输出层的节点位置；wk,i表示输出层到隐含层之间的权值，其中k表示输出层的节点位置，i表示隐含层的节点位置;θi表示隐藏层的第i个节点的阈值；ak表示输出层第k个节点的阈值[2]。

神经网络需要不断地训练、学习才能有更强的适应性。根据实际环境的变化，对权值进行调整，从而改善系统的性能。最初由于计算机发展技术的局限性，神经网络的层数复杂度以及训练程度、学习时间等较为不理想，导致算法最终效果并不太离想。现在随着计算机技术的发展，人工神经网络算法可以通过长时间、高精度的训练学习、以及增加节点数、层数等方法来提高计算的精度。

根据图1标示，BP神经网络算法的计算过程如下[3]：

1) 信号的正向传导

隐含层的每个节点输入输出以及输出层的每个节点输入输出如何计算。

隐含层输入Hi：

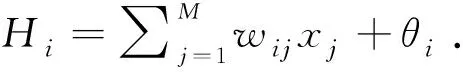
隐含层输出Oi：

(2)

输出层的输入Hk：

输出层的输出Ok：

(4)

2) 误差的反向传导

首先，输出层计算输出误差，然后隐藏层开始计算输出误差，直到输入层。通过不断计算误差，并不断调整各层的权值和阈值，直到最终的计算输出和原始目标在误差范围内。

对每一个训练样本p来计算它们的二次型误差准则函数Ep：

(5)

因此，总误差准则函数如下：

(6)

根据误差梯度下降法，依次修正，输出层权值的修正量Δwki：

(7)

输出层阈值的修正量Δak：

(8)

隐藏层权值的修正量Δwij：

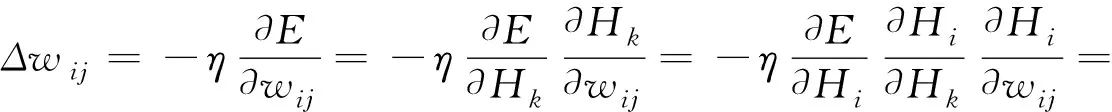
(9)

隐含层阈值的修正量Δθi:

(10)

BP神经算法，首先对权值、阈值进行初始化，接着提出训练样本，分别依次计算隐含层、输出层、各个神经元的输入和输出；再计算误差，分别依次计算输出层、隐含层误差。修正从输出层到隐含层的权值、阈值。接着判断样本是否全部训练完成，如果没有则接着从输入训练样本开始进一步训练。如果训练完成判断误差是否小于某个值，如果不小于则跟新训练总步长，重新从输入训练样本开始新一轮循环，如果小于则本轮训练结束。

2 BP神经网络函数逼近的MATLAB实现

2.1 构建BP网络函数逼近

利用MATLAB工具箱或者编程都可以构建BP神经网络函数算法。本文利用MATLAB编写m文件来实现对神经网络函数以及各个参数属性值的修改。并通过MATLAB基本图形可视化语句来实现函数逼近效果曲线的显示。从而可以十分简单直观地看到各个参数对于函数逼近效果的影响，是非常方便的研究学习方法。相对于完全编程方法来说，更加简单直观的了解利用不同函数建立网络的效果，而不需花费大量的时间在公式编辑上。而是利用更多的精力去寻找合适参数，合适方法，合适函数对不同目标进行拟合，甚至寻找不同算法结合出新的算法。本文通过MATLAB对简单函数的拟合逼近来掌握BP神经网络的基本结构，并了解哪些参数会对函数逼近效果产生影响。

设计一个BP神经网络，来逼近函数(11)：

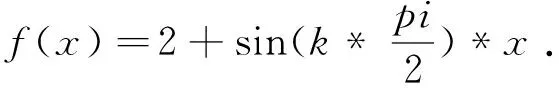
首先，设参数k=2。用newff函数来建立BP网络结构。利用newff函数建立的神经网络为一个隐含层。隐含层的神经元数目为n，是可以改变的。暂设设置为n=3，输出层有一个神经元。设置隐含层的传递函数为tansig函数，输出层的传递函数为purelin函数，网络训练采用Levenberg-Marquardt算法trainlm，关键代码如下：

n=5;

net=newff(minmax(p),[n,1],{' tansig' 'purelin'},' trainlm');

结果如图2所示，网络一开始建立的函数，权值、阈值的值是随机变化的，所以导致网络输出的结果很差，基本上不能实现原函数的逼近，而且会发现每次在MATLAB里运行程序时输出的曲线也不一样，正是由于在此过程中权值、阈值是随机变化的。

图2 网络输出曲线与原函数的比较

2.2 训练BP网络

由于只建立网络并不能达到函数逼近的效果，所以需要选择训练方式来对网络进行训练。本例利用MATLAB例的train()来对网络进行训练。将训练的时间设为200，训练精度设为0.2，其余参数采用默认值。

经过设定参数的训练后，得到了如图3所示的结果。从图中可以看出，和没有训练之前的曲线相比，训练之后的曲线和原函数的逼近效果更好。

图3 k=2,n=3网络输出

2.3 改变参数和隐含层神经元数目

函数中的k为频率，改变k和神经网络中隐含层的节点数目，会对神经网络对函数的逼近效果产生一定的影响。

假设参数k=2，n=10时，用之前同样的参数进行训练。输出结果如图4所示。

图4 k=2,n=10网络输出

从图4可以看出，当n=10时，经过训练后的曲线基本和目标曲线重合。和图3相比效果明显。说明增加隐含层的神经元数可以增加BP神经网络函数逼近的准确性[4]。

假设参数k=3时，隐含层神经网络数分别取值n=3、n=10，用同样的方法进行训练。假设参数k=6时，隐含层神经网络数分别取值n=3、n=10，用同样的方法进行训练。各个输出结果如图5所示。

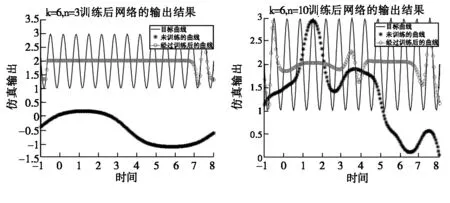
图5 不同参数网络输出

通过观察仿真结果，可知，相同频率时n=10时BP神经网络对于n=3时对函数的逼近效果较好。相同BP神经网络隐含层节点数时，k值越小对目标函数的逼近效果越好[5]。

3 结束语

本文通过构建BP神经网络，并对网络进行训练学习。研究了不同参数变化对神经网络对函数逼近的影响。通过MATLAB编写程序，对基本的BP神经网络逼近函数进行了仿真，通过结果图显然可见，神经网络通过训练之后的曲线比没有训练的曲线对原始函数的逼近效果好。改变函数的频率和隐含层神经元数目会影响函数逼近的结果。网络非线性程度越高，对于BP网络的要求就越高，也就是如果采用相同的网络，逼近效果就要差一些。一般来说，BP神经网络中，隐含层神经元数目越多，则逼近非线性函数的效果就会越好。

BP神经网络算法，其实是让误差尽可能地变小。由于此种算法中采用的下降方法会导致网络学习效率较低、收敛速度也不够快，可以采用一些别的比如RBF、自适应学习等方法来改进算法。这也是后续函数逼近时需要进一步改进的地方。