基于改进型遗传算法的电镀行车柔性调度设计

杜 斌，郭帝江

(中国电子科技集团公司第二研究所，山西 太原 030024)

1 绪言

随着电镀生产工艺流程越来越复杂，以及电镀产品呈现出小批量多品种的态势，这就需要电镀企业在电镀行车柔性调度方面达到更高层次的自动化、智能化[1]。通过学习发现国内外许多针对先进电镀产线制造系统[2-4]，镀件在工位间的搬运动作基本都是由计算机控制的电镀行车完成。目前，行车调度问题主要依赖于混合整数规划、分支定界以及绘画行车运行图等精确算法[5,6]。但上述算法只适用于求解小规模调度问题，在大规模复杂行车调度问题上，只能依靠智能算法求解。因此，对具备柔性调度的电镀行车而言能极大的提高整个生产线的生产效率，提升产品质量有着非常重大的意义。

本文依据企业的实际生产需求，为具有柔性电镀时间的电镀行车调度问题提出了一种改进型遗传算法(Improved Genetic Algorithm, IGA)。该算法中染色体编码方式采用电镀行车搬运次序，依据不同行车调度特征算法产生了初生代种群，同时，该算法通过在交叉变异操作中运用邻域运算，从而避免了迭代冗余，消除了传统遗传算法(Traditional Genetic Algorithm, TGA)中优化种群难以保证的缺点，加快了收敛速度。实验最后通过对电镀产线中的案例分别进行了测试对比，验证了该算法的可行性和有效性。

2 调度问题描述和模型建立

电镀产线中调度单元基本是由一组工艺、功能槽位和电镀行车组成。工位号为0、1、2…，N，N+1，其中0和N+1为上、下料工位。镀件在某个工位上i的浸渍时间ti具有一定的柔性范围，即ti的上下限值[ai，bi]。电镀行车是负责镀件在工位间进行搬运操作。行车将镀件从工位i搬运至i+1的动作称为搬运操作i，时间为dti(0≤i≤N)。电镀行车在工位i到j的空载时间是Ci,j(0≤i,j≤N+1)。镀件在工位上浸渍完成后须搬运至下一工位，所有镀件均已在上料区内整备，且行车与工位有且只能处理一个镀件。

◆ 示例模型

依据实际采用5个工位的行车调度产线，其中有效工位为3，si(0≤i≤3)表示行车搬运i的起始时间。因此，行车的搬运次序可看为(0,1,3,2)，在该周期起始时刻，行车会将镀件由上料工位搬运至工位1内，等待完成s1后再搬运至工位2，紧接着会空载行驶至工位3，并在s3取出在工位3内的镀件放置下料区，随后空载行驶至工位2，在s2搬运镀件进入工位3，行车继续空载行驶至上料区，在T继续下个周期运作。

为了便捷，将周期内的搬运次序定义为X=([0],[1],[2],…，[N])，si表示搬运i的起始时刻(0≤i≤N)。因此，镀件在工位i内的浸渍时间ti就是

ti=si-(si-1+di-1)+yiT.

(1)

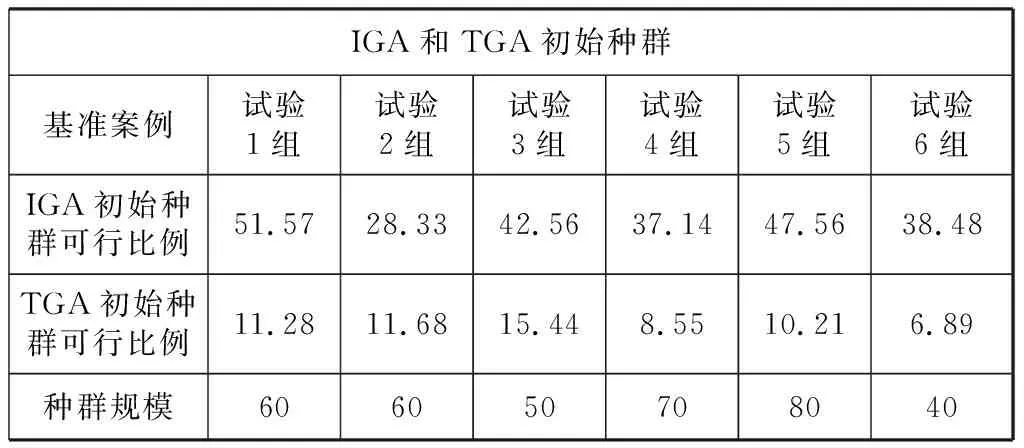
(1)式中，当si>si-1时，yi=0表示搬运动作i-1和搬运动作i搬运同一个镀件；相反，si

可得出电镀行车搬运调度问题的模型：minT。即：

s[i]≥0，0≤i≤N.

(2)

s[i]>s[i]-1时，yi=0；反之，yi=1.

(3)

s[N]+d[N]+c[N]+1,0≤T.

(4)

s[i]+d[i]+c[i]+1,[i+1]≤s[i+1].

(5)

a[i]≤s[i]-(s[i]-1+d[i]-1)+yiT≤b[i].

(6)

式(2)、(3)为镀件搬运过程中的约束条件；式(4)、(5)为电镀行车搬运约束条件,因此可将所研究的问题转化称为寻求一组电镀行车搬运周期次序X，使得该次序下周期T时间最小化。

3 改进型遗传算法结构的设计

3.1 算法编码

遗传算法作为全局寻优的智能方法，在解决大规模调度问题中得到了广泛应用。本次算法采用行车搬运次序的染色体编码方式，将搬运队列作为其“基因序列”，即X=(x0,x1,…，xN)为一个基因组。在图1示例中，对应的染色体编码为X=(0,1,3,2)。

图1 五个工位的产线调度示意图

3.2 初生代种群架构

初始种群的质量对算法后续优化有重要的影响，通过对电镀行车调度特征的研究，发现可行基因序列(可行搬运作业顺序)必须满足以下性质：

1) 在产线中每个周期内，只准许一个镀件进行和离开，并且行车每个周期内在每个工位上只能搬运一次；

2) 当镀件进入上料位后，若有K个工位被先前进入的镀件占用，则这K个被占用的工位上的搬运一定优先于近前工位上的搬运动作；

3) Chen等[14]对电镀产线中最大镀件数Kmax值的求解做了详细叙述。只有当k≤Kmax时，行车搬运次序才具备可行性。

因此，新初始种群的具体思路为：首先需要计算Kmax的值，分别设k为1，2，3，…，Kmax，随机产生k个镀件在工位上的P种排列情况，然后产生出满足以上三个性质的初始基因种群。

3.3 算法适应度函数

为了保证进入下一代的个体更加优良，算法中选择了经典的轮盘赌，即将上代中最优的个体随机替换掉下代中基因个体，从而保证该遗传算法的寻最优值继续进行。

因本文研究对象为行车调度问题的目标为最优周期T，因此，适应度函数为

F(X)=(Tmax-T)/Tmax.

(7)

其中:Tmax为种群中最大的周期，T为基因个体X对应的周期。

3.4 验证算法有效可行性

为了检验提出的算法是否具备有效性，该试验分别应用IGA和TGA对六组行车调度问题的基准案例进行测试比较。

假设电镀生产线由13个含有各种化学液体的工艺槽和一个负责搬运镀件的行车构成，镀件被行车依次搬运至工艺槽中接受除油、清洗、活化、电镀、钝化、烘干等电镀工序，其中镀件在每个处理槽中的浸渍时间被限定在一定时间范围内。六组行车调度问题基准案例的具体参数，如工位数N，浸渍时间范围[ai,bi]，行车搬运过程时间di和空载时间cij等都按照各自需要进行设置。同时，为了确保IGA和TGA两个算法的具备可比性，人为的将TGA和IGA的种群规模设置成相同，交叉概率Pc=0.6，变异概率Pm=0.9，算法的最大迭代次数为800。

表1中第1、2行数据分别表示为IGA和TGA产生初代种群中可行染色体比例，第3行为算法种群规模。由表1中数据可以看出，在每个试验组内IGA初始种群可行染色体比例明显均优于TGA的初始种群可行染色体比例。

表1 IGA和TGA初始种群

从表2中数据可以得出，IGA和TGA两个算法都可以在较短的时间内求到最优解。但在满意解方面，IGA的满意解优化更胜于TGA。

表2 IGA和TGA运行结果

图2中所示IGA和TGA这两个算法在示例中求解后的收敛曲线图。由图可得出IGA算法更加能够接近最优解，同时，由于算法过程中加入了相邻局部搜索方法，继而保证后续运算中IGA算法不断向最优解方向快速收敛。因此，可以得出本文所涉及到的IGA更为有效。

图2 IGA和TGA案例收敛曲线

4 结论

本文针对从电镀行业生产特点出发，为具有柔性电镀时间的电镀行车调度问题提出了一种改进型遗传算法IGA。该算法中染色体编码方式采用电镀行车搬运次序，依据不同行车调度特征算法产生了初生代种群，同时，该算法通过在交叉变异操作中运用邻域运算，从而避免了迭代冗余，消除了TGA中优化种群难以保证的缺点，加快了收敛速度。试验案例的实验结果表明，该算法在求解电镀产线中柔性电镀时间行车调度问题上具备了更高的可行性和有效性。同时，该算法已逐步应用于当前电镀产线控制系统中，表现良好，运行稳定。