基于2020年高考全国I卷第17题一类数列问题的研究
2021-02-05佛山市第一中学528000陈豪
佛山市第一中学(528000) 陈豪
中山大学数学学院(510275) 陈弈龙
在新高考中,数列大题出现在第一道解答题的位置,更多的是关注基本方法、基本思想,其中裂项相消法与错位相减法成为求前n 项和的最基本的两类方法,2020年全国I 卷,III 卷第17 题均为基于数列通项公式:an=(an+b)·qn的求和问题,an是一个等差数列与一个等比数列的乘积.此类问题通常采用错位相减法来求和,然而错位相减法容易出错,而这次公比还为负,数学生更容易出错.考生此处失分较多,下文我们将专门研究这类数列的四种求和方法.
一、原题呈现
例1(2020年高考全国I 卷理科第17 题)设{an}是公比不为1 的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前项和.
二、解法汇总
1 错位相减法

2 待定系数法

3 幂级数法

4 构造法
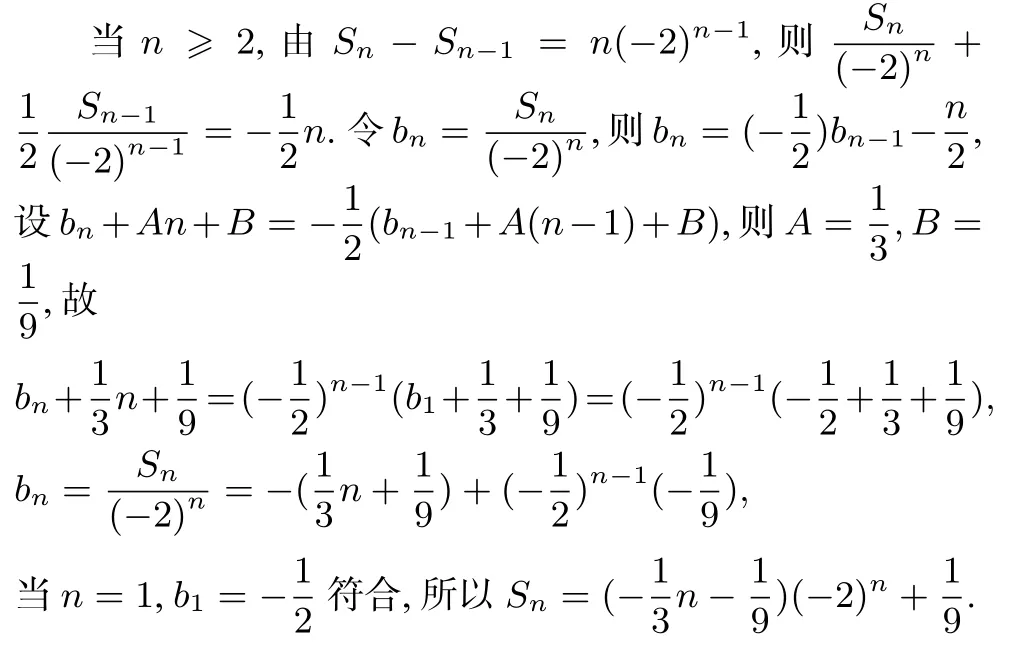
三、解法理论探索
1 错位相减法一般过程

2 利用待定系数法求an=(an+b)·qn前n 项和

3 幂级数法求an=(an+b)·qn前n 项和


4 构造法求an=(an+b)·qn前n 项和
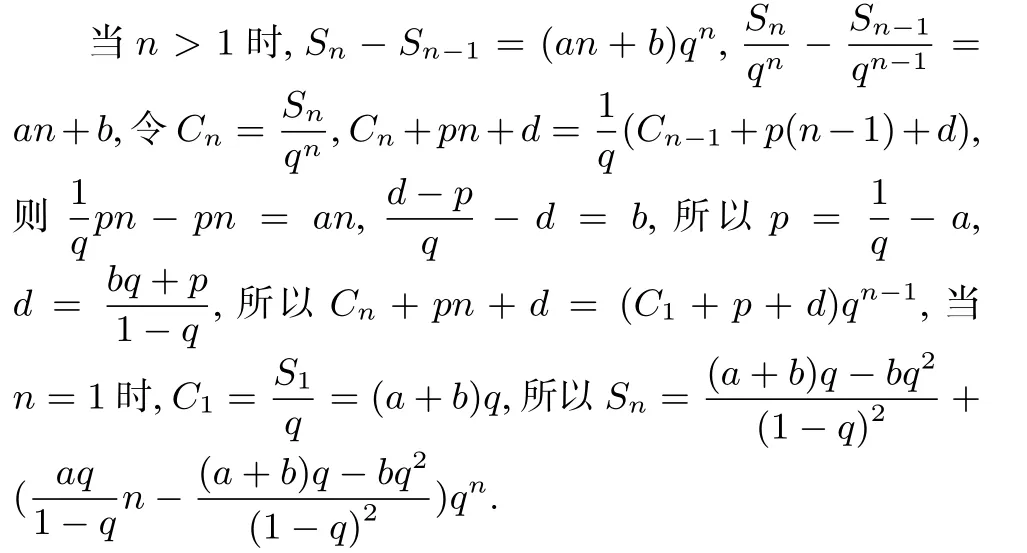
评析新课标重视基本方法基本能力,错位相减法为此类题的通法,能够较好地训练学生的计算能力与规范能力,传统方法老师讲过几十遍学生依然做不好[1],待定系数法则需要知道公式结果才行,特别适合选择填空的小题或者用来检验错位相减法的结果是否对,幂级数法则要将an=(an+b)·qn拆分为两个幂级数求和,需要看成函数利用导数来求和,高三总复习学生可以接受,构造法实质是化归成等比数列能够很好地锻炼学生的思维,高一学生也可以掌握.
四、练习补充
1.(2020 高考全国III 卷理科)设数列{an}满足a1=3,an+1=3an-4n.
(1)计算a2,a3猜想{an}的通项公式并加以证明;
(2)求数列{2nan}的前n 项和Sn.
2.(2011年高考辽宁卷)已知等差数列{an} 满足a2=0,a6+a8=-10.
(1)求数列{an}的通项公式;
3.(2010年高考新课标卷)设数列{an} 满足a1=2,an+1-an=3·22n-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n 项和Sn.
五、推广与应用


评析从例1,例2 中也显然可以看出,待定系数法、幂级数法和构造法都要比错位相减法更加地简洁且不易出错,构造法的计算量比错位相减与幂级数法是要小.而待定系数法由于课本没有相应的定理与结论,所以对于选择填空题可以优先选取,对于低次的求和问题,它来的最快;对于大题中遇到这类问题,可以考虑用待定系数法进行检验,当通项公式为高次时,传统的错位相减法要多次才可以,这时候可以分成若干个幂级数求和更方便.
