矩阵等价、相似、合同的区别与联系
2021-02-04李伯忍
李伯忍

摘 要:矩阵的等价、相似与合同在线性代数课程教学中占据非常关键的地位,但是学生学习过程中对这一部分的内容往往很难准确把握。为此,本文针對它们之间的区别和联系进行探讨,为学生对这些概念的理解提供一定的帮助。
关键词:等价;相似;合同
中图分类号:G4 文献标识码:A doi:10.19311/j.cnki.1672-3198.2021.04.065
《线性代数》是大学数学中的一门非常重要的必修基础课程。学好这一门课程,不仅有利于对学生的理解和逻辑推理能力的培养与训练,而且对其后续专业课程的学习也发挥着极其重要的支撑作用。
本文将就线性代数课程矩阵之间的非常重要的关系:矩阵的等价、相似与合同进行讨论,着重探讨三者之间的区别与联系,为学生对这些概念的理解提供一定的支持。
1 基本概念
矩阵等价定义:假定矩阵A和B为同型矩阵,若存在可逆的矩阵P,Q,满足PAQ=B,那么称A和B是等价的。
矩阵相似定义:假定矩阵A和B均为n阶方阵,若存在可逆的矩阵P,满足P-1AP=B,那么称A和B是相似的。
矩阵合同定义:假定矩阵A和B均为n阶方阵,若存在可逆的矩阵P,满足PTAP=B,那么称A和B是合同的。
2 区别和联系
(1)矩阵的等价只是要求矩阵A和B是具有相同的行和列的矩阵,不要求必须是方形矩阵,但是相似和合同则要求矩阵A和B必定是同阶的方形矩阵。
(2)等价的矩阵、相似的矩阵以及合同的矩阵均是同可逆或者同为不可逆。
(3)等价的矩阵、相似的矩阵以及合同的矩阵均满足反身性、对称性和传递性。
(4)矩阵的等价、相似以及矩阵合同实际上均是矩阵和矩阵之间进行初等变换,只是初等变换的要求有些区别。
详细的说明展示如下:
依据可逆矩阵的充要条件,n阶方形矩阵阵A是可逆的矩阵A等于一系列初等矩阵的乘积。
可见等价变换是对矩阵作一系列的有限次初等行或列变换;相似变换和合同变换也是作一系列的有限次初等行或列变换,但行变换的次数与列变换的次数是相同的,而且矩阵行变换与矩阵列变换的变换方式是相对应的;相似变换要求作一次矩阵列变换,相应的也要求作一次矩阵逆行变换;合同变换要求作一次矩阵列变换,也相应的作一次相同的矩阵行变换。
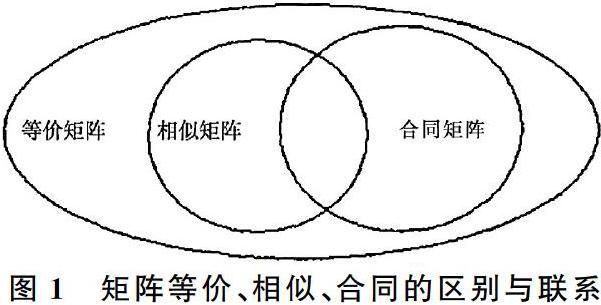
3 文氏关系图
4 如何判定矩阵与矩阵之间的相互关系
在判定矩阵的等价关系、相似以及合同关系时,满足矩阵等价、矩阵相似或者矩阵合同的两个矩阵的秩都必定相等,再适当的利用特征值与正负惯性指数来判定矩阵相似或者矩阵合同。
(1)矩阵A与B等价R(A)=R(B)。
(2)判定矩阵相似的四个必要条件:①A与B的秩相等;②A与B的特征值相同;③A与B的特征多项式相等;④A与B的行列式相等。
假定满足上述的必要性,我们还不可以判定矩阵是相似的,如何判别两个一般矩阵的相似,一般考试大纲不做要求,但如果矩阵A和B均与一个对角阵相似,那么可由相似矩阵满足传递性,可以知道A和B是相似的。
(3)对实对称矩阵,有一些非常重要的结论,可用于判断矩阵是相似的或者是合同的:①A与B均是实对称矩阵并且是相似的矩阵A和B的特征值相同;②A与B均是实对称矩阵并且是合同的二次型xTAx和xTBx的正负惯性指数是相同的;③A与B均是实对称矩阵并且是相似的A与B必定是合同的。
矩阵的合同主要应用于二次型,故判定矩阵是否合同的前提主要是在实对称矩阵的前提下进行,所以实对称矩阵A和B是否合同,只需要判定矩阵A与B的特征值符号是否一样;矩阵相似是指两个矩阵的特征值相同;矩阵等价是指两个矩阵的秩相等。
5 矩阵的等价、相似以及合同关系,有下面的几个结论
(1)矩阵A和B是相似的,则矩阵A和B一定是等价的,反之不一定成立。
(2)矩阵A和B是合同的,则矩阵A和B一定是等价的,反之不一定成立。
(3)若矩阵A和B均是实对称矩阵且相似,则矩阵A和B一定是合同的,反之则不一定成立。
参考文献
[1]同济大学数学系.工程数学线性代数[M].北京:高等教育出版社,2016.
[2]周勇.线性代数[M].北京:北京大学出版社,2018.
[3]孙瑶,杜润梅.线性代数中两个矩阵相似、合同、等价的关系[J].教育,2015,(46):251.
