故障救援情形下的地铁列车调度调整模型

朱巧珍，柏 赟，闫冬阳，曹耘文，贾文峥

（1.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3.上海申通地铁有限公司 上海轨道交通运营管理中心，上海 200070；4.交通运输部科学研究院 城市交通与轨道交通研究中心，北京 100029）

当地铁列车在正线上发生故障无法继续运行时，为避免故障列车长时间占用区间正线，需要组织故障救援，即通过其他列车与故障列车连挂，以救援协助方式使之及时驶离正线［1］。在列车救援期间，由于地铁车站配线较少，列车无法越行，救援列车与故障列车连挂、清客等操作将造成运营中断、原计划时刻表不再可行、部分列车运行间隔增大，进而使乘客服务水平下降。此时，行车调度员一般会加开线路备用列车，并调整相关列车的停站时间或区间运行时间，尽可能使运行间隔少增大，从而避免服务水平大幅度下降。

根据轨道交通系统受到扰动程度的不同，国内外学者主要从干扰和中断2 个层面研究了列车调度调整问题［2］。针对前者，文献［3］构建了以列车尽可能快地驶离列车晚点区段为优化目标的运行调整整数规划模型，设计基于优先规则的启发式算法，求解模型的可行解；文献［4］提出了地铁晚点列车在“赶点”运行调整措施的基础上，后续列车需要实行“延赶结合”调整策略，达到消除晚点传播根源的目的；文献［5］针对传统运行调整优化模型在求解效率方面存在的问题，构建列车运行调整的马氏决策过程模型，最小化列车的加权总晚点时间。针对后者，文献［6-7］以区间能力部分或完全失效情形为研究对象，合理安排上下行列车通过每个区间（尤其是故障区间）的顺序和到达、发车时刻，最大程度减小故障对列车运行的影响；文献［8］指出仅调整列车到发时分的效果非常有限，有必要结合其他运行调整措施，进一步消减服务中断的负面影响。需要指出的是，近年乘客服务水平备受关注，列车调度调整优化的目标也随之逐渐从列车相关指标转移到以乘客需求为导向的指标，比如文献［9-10］将乘客晚点、乘客总旅行时间作为调度调整的衡量指标。

在轨道交通列车调度调整中，加开备用列车也是降低站台滞留人数、提高旅客服务水平的有效措施之一。文献［11］讨论了备用列车开行的最佳时机，但作者只给出了基于经验的定性分析，缺乏精确数学模型。文献［9］和文献［12］针对铁路运营中断情形，考虑列车和乘客2 个方面的评价指标构建数学模型，求解最优的加开列车数量。这2 个模型针对网络层面的列车调度调整，虽然考虑了列车运行交路的调整，但由于问题规模过大，并未优化列车区间运行时间和停站时间，不适合于地铁线路的列车调度调整。文献［13］针对地铁列车中断运行结束后，相关的沿线各站累积大客流的情形，在固定加开备用列车数和方向的前提下，以列车到发时间、列车间次序作为决策变量，使最后1列列车到达终点站的时刻最小。文献［13］虽对列车到发时分进行调整，但固定了加开列车的数量与方向，缺乏列车调度调整的灵活性，仍有进一步优化空间。

本文以启动列车救援时刻的轨道交通运营状况为已知条件，考虑灵活的备用列车加开数量和加开方向，构建以列车到发时间和备用列车加开方案为决策变量、以站台滞留人数和加开备用列车数的加权和最小为优化目标的混合整数规划调度调整模型，并采用该模型优化故障救援情形下的列车调度调整方案。

1 前提假设

结合实际地铁列车故障救援时的调度调整，做出以下假设。

（1）对于运行列车突发故障导致车站可能出现的大客流现象，车站一般会采取站外限流等措施来保证站台安全，故不考虑站台滞留人数的上限约束。

（2）救援方案固定。正线运行的列车发生故障需要救援时，应首先遵循“顺向救援”原则，一般采用相邻后续列车正向推进故障列车的方法进行救援［14］。

（3）各个车站乘客的到达时间服从均匀分布［15］。

（4）调度调整期间，仅有救援列车和故障列车清客、限速运行。其他列车通过最小行车间隔时间来保证行车安全。

（5）可加开的备用列车包括运营前为防止突发事故而存放在存车线的备用列车和承担救援任务的救援列车。

2 数学模型

2.1 模型参数及变量定义

定义如下模型参数：Nns为车站总数；Ne为所有列车数量；Na为备用列车数量；S为车站集合，S={sj，j=1，2，…，Nns}；LEA为列车集合，包括既有列车和备用列车，LEA={li，i=1，2，…，Ne}；LA为备用列车集合，LA={lb，b=1，2，…，Na}，LA∈和分别为最小、最大区间运行时间；和分别为最小、最大停站时间；和分别为最小、最大折返时间；和分别为最小发发间隔、到到间隔及发到间隔时间；C为列车容量（常数）；为在救援前期准备时段Ta内列车救援所影响车站及区间的集合，包括影响车站和影响区间；α和β分别为乘客滞留人数和备用列车加开数的权重系数；和分别为第sj个车站站台乘客的到达速率及下车比例；M为很大的正整数，用于非线性模拟的线性化。

定义如下决策变量：为列车li到达车站sj的时刻；为列车li在车站sj的发车时刻；xi为0-1决策变量，若列车li为既有列车，则取值为1，若列车li为备用列车，则取值为0；为0-1 变量，若备用列车b从车站sj加开，则取值为1，否则取值为0。

定义如下中间变量：为0-1 中间变量，若xi=0 且sj为不可加开备用列车的车站，则取值为0，否则取值为1；ηi为0-1 中间变量，若备用列车li的加开时间大于0，则取值为1，若备用列车li的加开时间等于0 或li为既有列车，则取值为0；为到达站台乘客数，表示列车li离开车站sj与列车li-1离开车站sj的时间间隔内，该车站进站到达站台的乘客数；为下车乘客数，表示列车li在车站sj下车的乘客数；为上车乘客数，表示车站sj乘上列车li的乘客数；pi，j为在车乘客，表示列车li从车站sj-1发车时或者列车li到达车站sj时车内的乘客数；为站台滞留乘客数，表示列车li从sj车站发车后，因列车容量限制，仍滞留在站台的乘客数；为站台累积乘客数，表示列车li到达车站sj时站台的总乘客数。

2.2 优化模型

2.2.1 目标函数

列车故障救援情形下，调度调整的目标是最小化站台滞留人数和加开备用列车数的加权和Z，即

2.2.2 约束条件

1）列车运行时间约束

考虑列车运行速度限制，列车区间运行时间需满足不小于区间最小运行时间、不超过最大允许时间约束，即

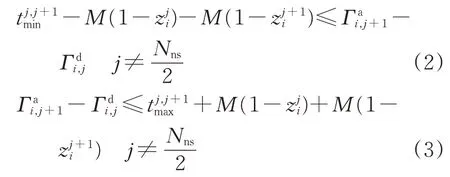
为保证乘客上下车顺利进行，列车最小、最大停站时间应满足停站时间上下限的约束，即

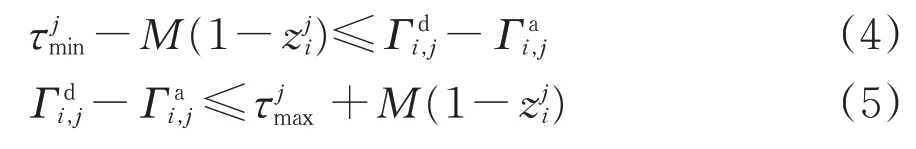
列车运行至终点站时需进行折返作业改变运行方向，因此列车折返时间应满足最小、最大折返时间约束，即

相邻列车的发车间隔、到站间隔和发到间隔分别应满足最小发发间隔、到到间隔和发到间隔的约束。设列车li′为列车li的后方列车，则有

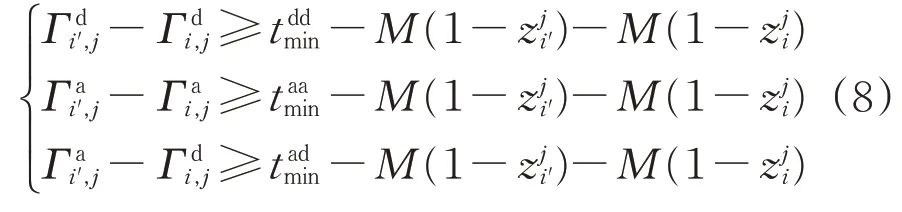
2）到达、发车时间约束

所有列车的到、发时间应分别大于等于研究时段起始时刻；若备用列车为救援列车，则到、发车时刻也应分别大于等于救援列车最早可加开时刻tb（tb的计算方法参见第2.4.2节），即

3）故障救援区段约束

故障救援区段如式（10）所示。从故障发生至救援结束之前，为避免潜在的危险，救援列车的后方列车不能进入故障救援区段，即救援列车后方的第1 列列车li需在原车站停车等待直至救援结束，即

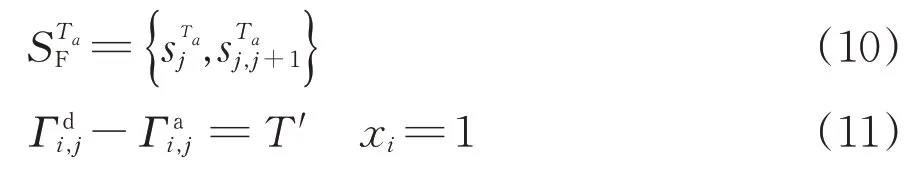
4）备用列车加开位置及方向约束

位于车站sj的备用列车lb，至多只能从车站sj的上行或者下行方向加开，即

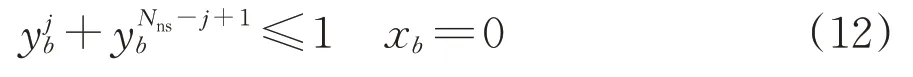
2.3 客流计算

以乘客到达站台速率为基础，考虑列车能力，计算各车站在发车间隔内到达站台的乘客数、上下车人数、在车人数、站台滞留人数和站台累积乘客数。

到达站台乘客数的计算式为

上行或下行起点车站的下车乘客数均为0，列车在其他车站的下车乘客数用下车率乘以在车乘客数来表达，即

上行或下行方向最后1 个车站的上车乘客数也均为0，其他车站的上车乘客数应取想乘坐该车次的人数和能够乘坐该车次的人数之中的最小值，即

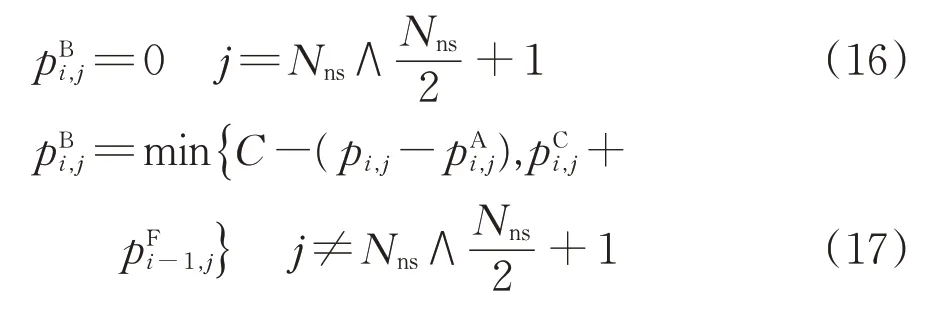
可见，式（17）为非线性模型，因此，引入0-1变量ξi，j和最大数M，将其线性化，即

位于上行或下行方向第1 个车站的列车，其在车乘客数为0，列车到达其他车站时的在车乘客数为列车离开上1 个车站时的在车乘客数减去上1 个车站的下车人数，再加上在上1 个车站的上车人数，即

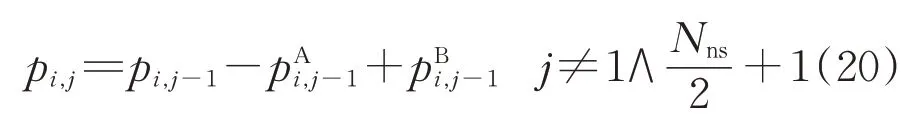
站台滞留乘客数的非线性表达式为

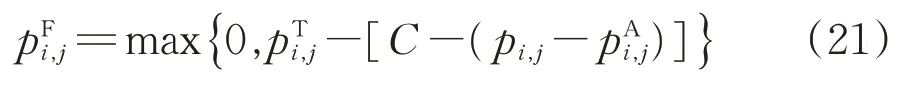
可见，式（21）也为非线性模型，因此，引入0-1变量ςi，j和最大数M，将其模型线性化，即

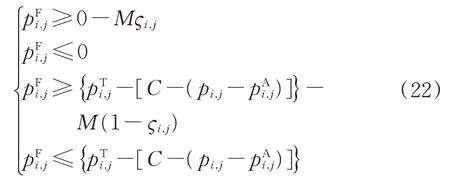
站台累积乘客数包括上1 列列车离开该车站时滞留的乘客数和该发车间隔内到达的乘客数，即

2.4 救援时长和救援列车最早可加开时刻计算

2.4.1 列车救援时长

由于列车救援时长会影响救援列车作为备用列车的可加开时间、救援列车后方列车可进入救援区段的时间，进而影响模型调整方案。因此，有必要根据故障列车和救援列车的位置分别计算救援前期准备时长T准（即Ta）和列车推送时长T推。其中，前期准备工作包括启动列车救援至救援列车与故障列车连挂成功且2 列列车完成清客；列车推送作业为连挂并清客完成后救援列车将故障列车推放至就近的存车线或停车线。启动列车救援时，不同位置下的救援列车和故障列车操作时间示意图如图1所示。

故障列车位于车站、救援列车分别位于车站和区间的前期准备时长T准的计算式为

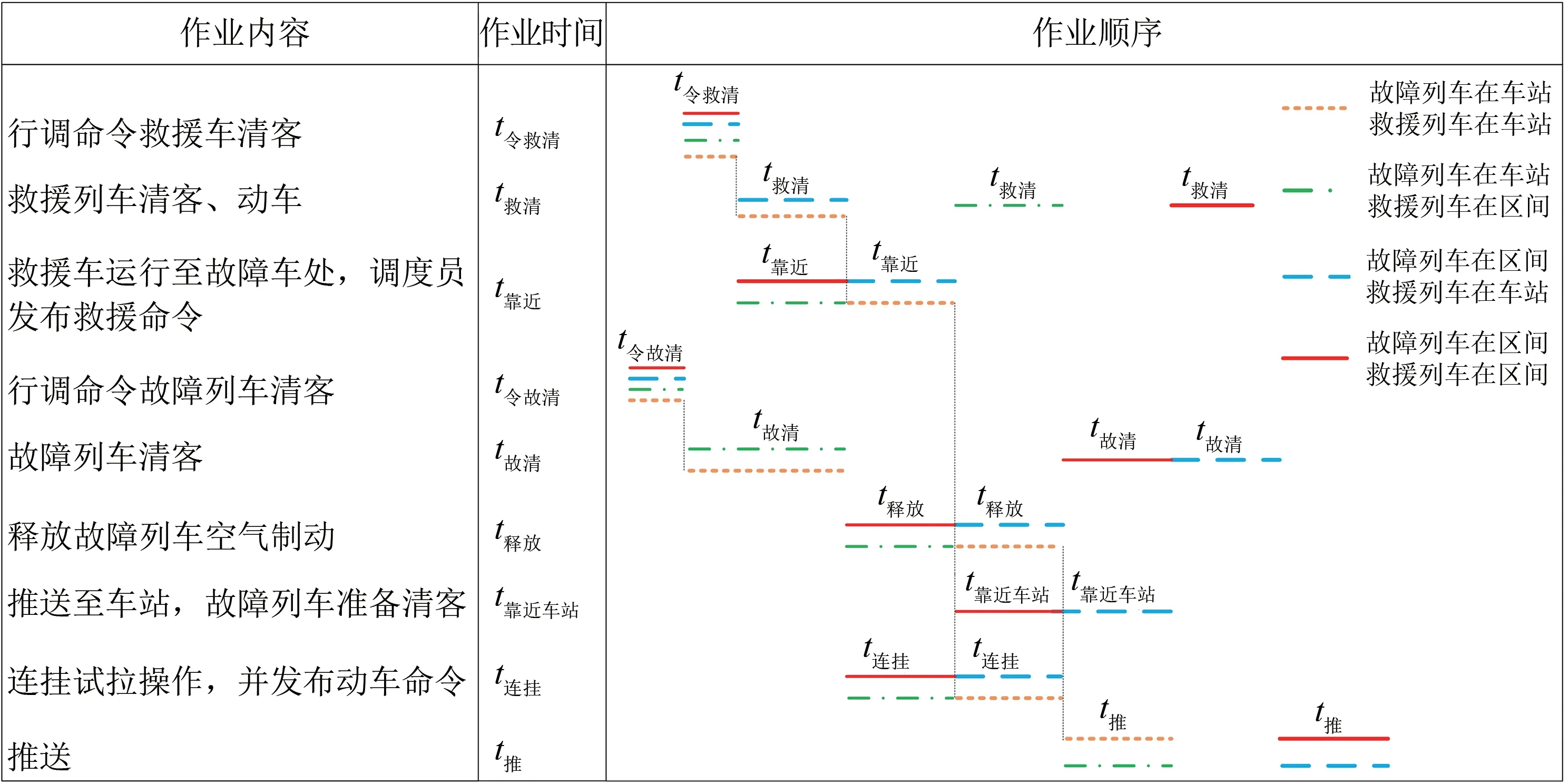
图1 不同位置下的救援列车和故障列车操作时间示意图

故障列车位于区间、救援列车分别位于车站和区间的前期准备时长T准的计算式为

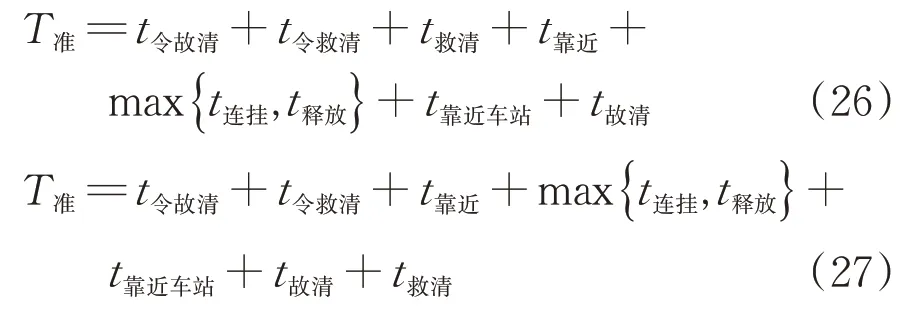
救援列车推送故障列车的时长T推的计算式为

式中：L推进为推进距离，m；v推进为推进速度，m·s-1；t启和t停分别为列车的起动、停车附加时间，s。

2.4.2 救援列车最早可加开时刻

救援列车将故障列车推送到停车线后，故障列车与救援列车进行解钩的时间记为T解；救援列车为下一次继续上线运行做准备的时间记为T准备。令t启动救援为启动列车救援的时刻，则救援列车的最早可加开时刻为

3 案例分析

上述模型采用MATLAB 的YALMIP 工具包并调用CPLEX 12.6.2求解。本文案例的求解过程在2.50 GHz CPU和8 GB内存的计算机上完成。

3.1 案例描述及模型参数设置

以某地铁运营线路为案例，如图3 所示，验证上述方法的合理性和有效性。设列车从车站A 运行至车站L 为上行方向，从车站L 运行至车站A 为下行方向。现有010 次列车于上行车站E 发生故障，经司机确认无法动车，需要启动列车救援组织。行车调度员派故障列车的后方第1 列列车012次（该列车位于上行车站D）进行救援，将故障列车推送至故障前方停车线，该停车线位于车站F。该列车发生故障时，线路存有2 列备用列车，其中，备用列车1 位于车站I，备用列车2 位于车站L。车站I 和车站L 存车线的布设形式均满足备用列车从上行方向或者下行方向均可以加开的条件。需要注意的是，备用列车若从上行方向开出，则需要满足反向加开的最小行车间隔要求（包括司机换端时间）。

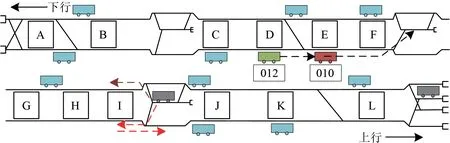
图2 地铁线路示意图

案例基本参数设置见表1。列车最小间隔时间（包括发发间隔、到到间隔和发到间隔）为210 s，最小和最大折返时间分别为180 s 和240 s；最小和最大停站时间分别为30 s和60 s；列车定员为1 440人。设定列车满载率超过一定阈值（本文设为70%）时才加开备车，因此取站台滞留人数权重系数α=1，加开备用列车成本的权重系数β=1 000。

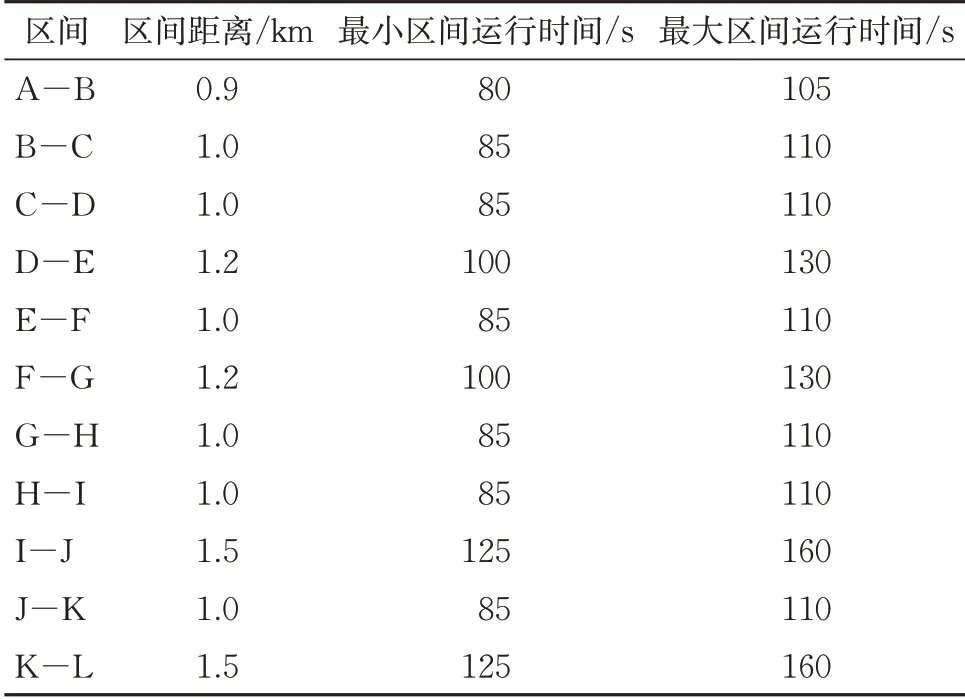
表1 基本参数设置

图1 中的场景为启动列车救援时，故障列车和救援列车均位于车站。该场景下，采用式（24）、式（28）和式（29）计算可知，启动救援至推送开始的时长为886 s，开始推送至救援列车可加开的时长为529 s。

3.2 备用列车加开方案对比

首先，采用本文的模型优化得到不固定加开列车数量的备用列车加开方案（简称为不固定加开列车数量方案）。同时，为了验证本模型的效果，引入固定加开备用列车数量的方案，即仍然采用本文的模型，只是将目标函数式（1）中∑ηi分别取值为0，1，2 和3 得到的优化方案，视其中取值为0时的方案为不加开备用列车。优化结果如表2 和图3所示，分析表2和图3可得如下结论。

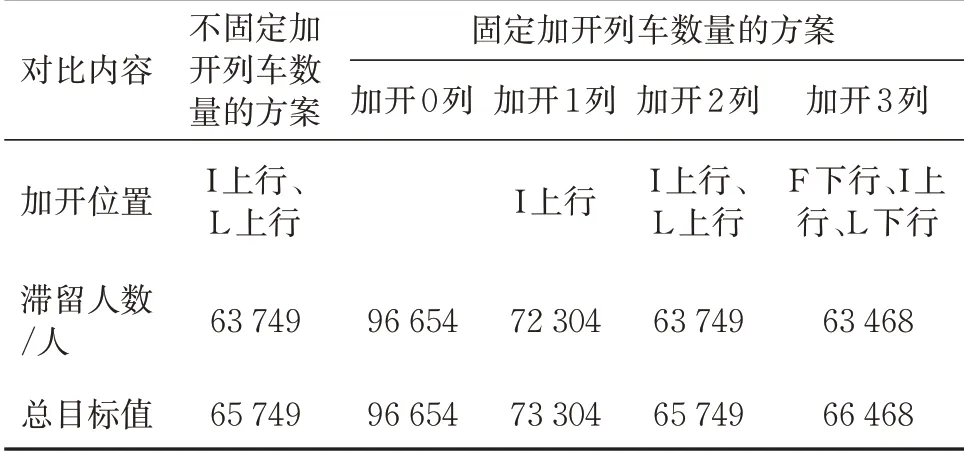
表2 不同加开备用列车的方案对站台滞留人数的影响

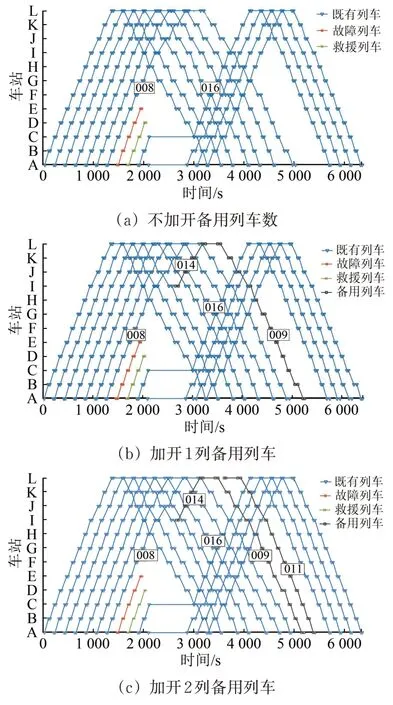
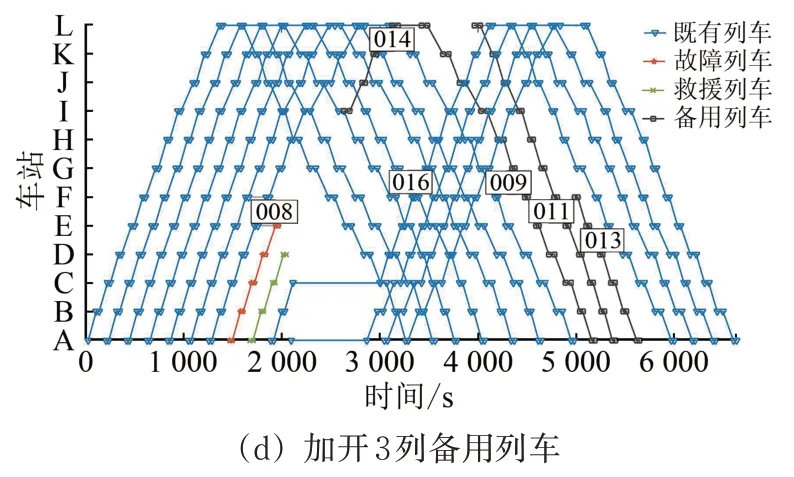
图3 不固定、固定加开列车数量的列车运行调整图

（1）采用本文的模型和算法可求得最优的备用列车加开方案和列车运行调整方案。模型的求解时间约为2.0 min，备用列车启动时刻是在列车救援启动12.6 min 之后，所以，该求解时间满足列车故障救援情形下的调度调整要求。

（2）不固定加开列车数量的方案为：加开2 列备用列车，分别位于车站I 和车站L，该方案与固定加开2 列备用列车得到的优化结果相同，相应的运行调整方案如图3（c）所示，滞留人数为63 749人。从车站I 反向发车的备用列车与前车在车站I的到发间隔为406 s，满足反向加开的最小行车间隔时间要求［16-17］。

（3）与加开0 列备用列车和加开1 列备用列车方案相比，不固定加开列车数量方案中的滞留人数减少了34%和11.8%，总目标值也有所降低。其原因是，图3（a）中008 次和016 次、图3（b）中014 次和016 次列车之间存在较大的间隔时间，客流需求较大；当016 次到达各站台时，因列车容量限制，难以带走站台累积的乘客，致使站台滞留人数增多。

（4）与固定加开3 列备用列车方案相比，不固定加开列车数量方案中的滞留人数虽然增加了0.4%，但总目标值降低了11%。加开2 列备用列车填补了故障造成的大间隔后（图3（c）），共计有63 749人的站台滞留人数，其中63 468人为上行方向车站A至车站K的滞留人数，其余的滞留人数为下行方向车站D和车站C的滞留人数。从下行方向加开的013 次列车只能运走下行方向车站D 和车站C 滞留的281 人，即加开的第3 列备用列车只能很小幅度地减少滞留人数。因此，加开2 列备用列车是最优的方案。

3.3 敏感性分析

3.3.1 备用列车存放位置对备用列车加开数量和加开方向的影响

基于图2 所示的实例线路，采用本文的模型和算法，进行参数敏感性分析。该线路共有4条存车线，分别位于车站B，F，I，L，且1 条存车线同一时间最多只能存放1列备用列车。目标权重系数仍然取α=1，β=1 000，优化得到备用列车数量和存放位置变化下的备用列车加开数量、加开位置和滞留人数，结果见表3。

表3 备用列车数量和存放位置变化对滞留人数的影响

分析表3可得如下结论。

（1）以表3 中2 列备用列车的情景为例进行分析可知：备用列车共有6种可能的存放位置组合方案，每种方案的列车加开数量为1 或2，站台滞留人数不尽相同。由此可见，当备用列车数量一定时，备用列车加开数量和站台滞留人数均会受到备用列车存放位置的影响。

（2）故障列车存放在车站F，备用列车存放在车站I，则加开故障列车存放位置前方车站的车次014 是不固定备用列车加开数量方案的首选列车，如图3 和表3 所示。由此说明，优先选择加开故障列车存放位置前方车站的备用列车，有利于同时填补上行和下行因故障增大的行车间隔时间，尽早带走更多的乘客。

（3）建立模型时考虑了灵活的备用列车加开方向，即不固定备用列车的加开方向。因此，上行方向发生故障时，从表3 中的第4 列看出，位于车站F 的备用列车是从下行方向加开的；位于车站I 的备用列车是从上行方向加开的。这是因为，不固定加开列车数量方案中，故障救援导致列车不能在救援时间段内通过上行的故障影响区段（如图3中车站D—车站F），因此，故障影响区段前方的备用列车应遵循“沿故障发生的方向加开”，故障影响区段及其后方的备用列车应遵循“沿故障发生方向的反方向加开”的原则。

综上所述，列车故障救援情形下站台的滞留人数主要受备用列车加开数量的影响，而备用列车加开数量又受备用列车存放位置的影响。因此，在运营开始前，调度员需要合理地安排备用列车的存放位置和数量。

3.3.2 目标权重系数

优化目标中滞留人数、备用列车加开数的权重系数α和β的取值对目标会有较大的影响，因此本节对α和β的取值进行敏感性分析。取权重系数α=1，β=0，1，100，331，500，…，50 000，模拟计算目标权重系数的影响，结果如图4所示。

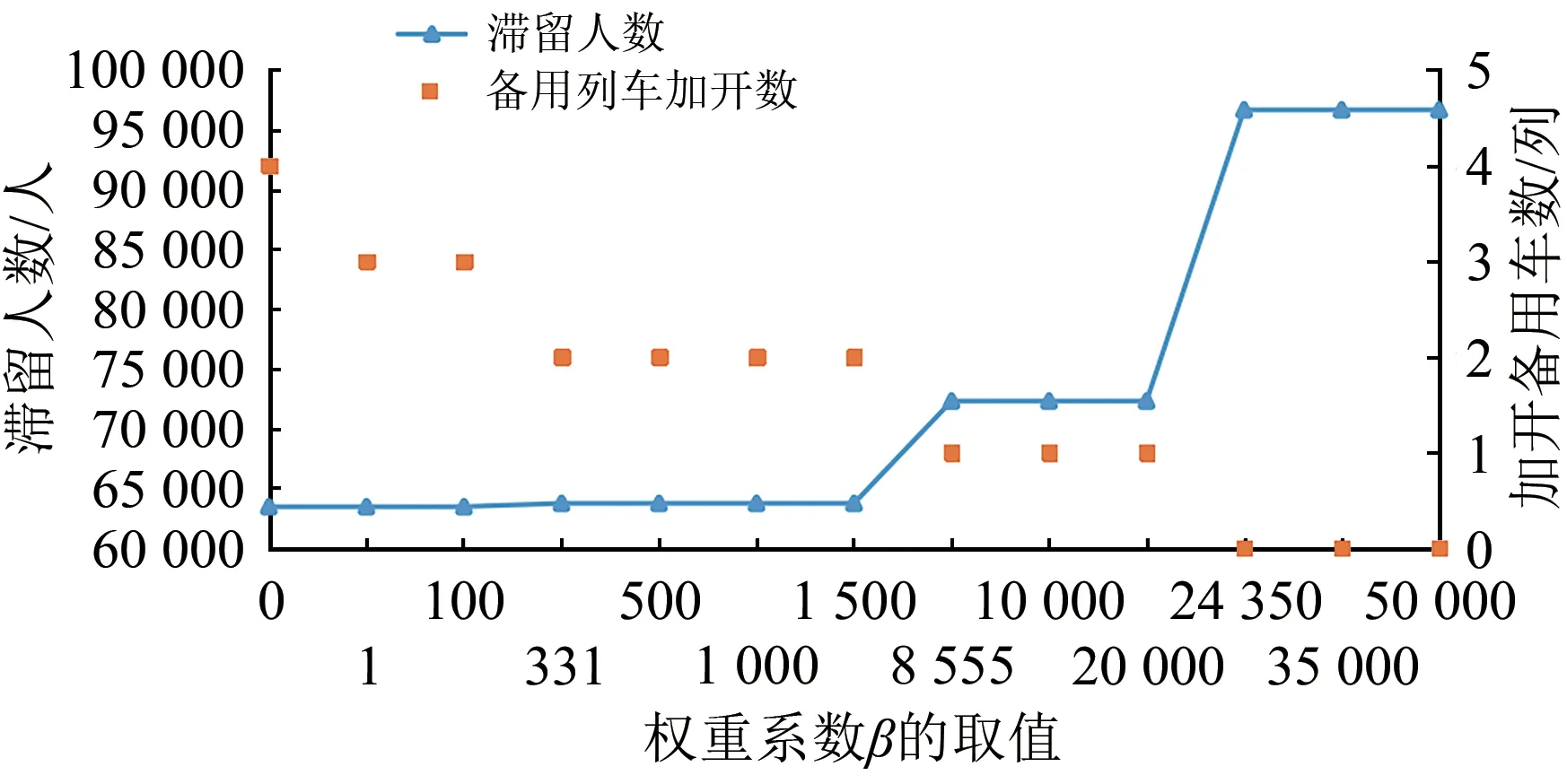
图4 目标权重系数α和β对滞留人数和备用列车加开数影响

由图4 可知：备用列车加开数权重系数β的取值不同，所得方案的乘客滞留人数与备用列车加开数会有所不同；β取值不小于24 350 时，不加开备用列车，β取［8 555，24 350）时，加开1列列车，此时，滞留人数降低了24 350人；β取［331，8 555）时，加开2列列车，与加开1列相比，滞留人数减少了8 836人；β取［1，331）时，加开3 列列车，与加开2列相比，滞留人数仅仅减少了281人；β取0时，加开4 列列车，相较加开3 列，滞留人数不再变化。这是因为客流总需求一定，加开2 列备用列车时，基本上可带走大部分的站台等待乘客；继续加开更多的列车，受到列车救援及备用列车存放位置的影响，已无法带走更多乘客，故滞留人数基本不变。

根据设定的列车预期满载率为70%，考虑到列车定员为1 440人，因此该案例权重系数α=1，β=1 000。在实际应用中，调度人员可结合加开成本以及客流需求，选择不同的目标权重系数。

4 结 论

本文针对列车故障救援情形下的地铁列车调度调整问题，以备用列车的加开方案和列车的到发时刻为决策变量，以站台乘客滞留人数和备用列车加开数的加权和最小为优化目标，建立了混合整数线性规划调度调整模型，该模型考虑了列车运行时间、备用列车加开位置和方向、故障救援区段限入、客流量等约束。案例分析结果表明，相较于固定加开列车数的方案，不固定列车加开数量方案的模型在降低站台滞留人数的同时减少备用列车加开数量，能较好地解决故障救援情形下的调度调整问题。

采用该模型分析备用列车存放位置对备用列车加开数和加开方向的影响可知，备用列车的存放位置会影响备用列车的加开方案以及站台滞留人数。同时，可以得到备用列车加开方案的一般规律：应优先选择加开故障列车存放位置前方车站的备用列车；故障影响区段前方的备用列车应沿故障发生的方向加开，故障影响区段及其后方的备用列车应沿故障发生方向的反方向加开。因此，在地铁线路运营前合理安排备用列车的存放位置、运营过程采用以上备用列车的加开规律，可降低列车发生故障后的站台滞留人数，提高地铁服务水平。在实际应用中，调度人员还可结合加开成本以及客流需求，选择不同的目标权重系数。

列车故障救援情形下的调度调整是复杂的决策问题，本文模型从故障线路角度出发，仅调整了故障线路的列车运行过程。而随着轨道交通网络化发展，列车故障可能会通过换乘车站影响其他线路乃至整个网络。因此，下一步工作将从轨道交通的网络化层面着手，考虑多种调整策略相结合的优化问题。