基于牵引电缆的电气化铁路牵引网长距离供电方案

王 辉，李群湛，刘 炜，王 创，刘童童

（西南交通大学 电气工程学院，四川 成都 611756）

市域铁路具有站间距离短、再生制动能量占比高、选址困难等特点，当前其牵引供电系统多按照干线铁路供电方式进行设计［1-2］；重载铁路机车为大功率牵引负荷，部分线路存在重负荷下坡、轻负荷上坡、再生制动能量利用率低的情形，为提升运量采取了一系列有益措施，但仍有一定不足［3-4］；以青藏线和川藏线为代表的高原电气化铁路建设面临外部电源薄弱、桥隧占比高、长大坡道多和不宜过多设置电分相等难题［5］。上述现状对既有牵引供电系统提出了更高要求和新的挑战，如减少线路中的电分相数目，增加牵引变电所选址的灵活性，在满足供电能力且安全可靠的前提下实现长距离供电。

牵引供电系统的电压损失由牵引变压器电压损失和牵引网电压损失共同构成，是衡量牵引供电系统供电能力和供电距离的重要指标之一。牵引供电系统的电压损失越小，牵引网的供电距离越长。减少牵引变压器电压损失最直接的方式是提高牵引侧母线电压，也可安装节能变压器，在牵引变压器牵引端口设置补偿装置等。减少牵引网电压损失的措施有选择阻抗较小的牵引网线材、设置补偿装置、改进供电方式、提高列车的功率因数等。对于既有AT 供电等供电方式，通过增加加强导线、复线铁路采用上下行全并联方式等措施，可降低牵引网的电压损失、延长牵引网的供电距离。采用新技术和新型供电方式也可达到延长牵引网供电距离和减少电分相的目的。文献［2］研究了一种适用于市域铁路的牵引供电方案，在传统牵引网供电方式的基础上，在牵引变电所和牵引网中设置静止无功发生器（Static Var Generator，SVG）。文献［5］研究了一种牵引变电所群贯通供电系统，可实现多个牵引变电所的贯通供电，但要求外部电源构成树形结构供电。文献［6］提出在牵引变电所设置同相补偿装置，取消变电所出口处电分相，并指出前苏联等国采用双边供电来增加供电距离，可取消分区所处电分相，但存在均衡电流等问题。文献［7］提出一种牵引电缆贯通供电系统，由牵引电缆和牵引网构成两级供电方式，二者之间通过单相变压器连接。文献［8］研究了一种同相贯通供电系统，但外部电源若不构成树形结构会带来均衡电流问题，需采取相应抑制均衡电流的措施。文献［9］介绍了一种采用16.7 Hz 制式的牵引供电系统，可实现贯通供电，但该供电制式成本较高，仅在德国、瑞典等国应用。

对于上述供电方式，通过降低牵引网的阻抗也可延长牵引网的供电距离，其有效途径是将牵引电缆（简称“电缆”）与既有牵引网通过横向连接线并联，形成基于电缆的电气化铁路牵引网（简称“电缆牵引网”）长距离供电方案。本文重点研究3 种电缆+AT 供电方式下电流分布和等值阻抗等电气特性；构建多列列车负荷的潮流计算模型，基于该模型，以列车工作电压为约束条件，提出确定电缆牵引网供电距离的方法，通过电气特性对比和实例计算，说明所述方案的有效性和优越性。

1 电缆牵引网长距离供电方案

目前，我国电气化铁路供电方式主要有直供方式和AT 供电方式2 种，其中AT 供电方式分为日本方式、法国方式和新型方式［10-11］，它们的结构区别在于靠近牵引变电所处的第1 个AT 段内AT变压器的连接方式不同。则电缆牵引网长距离供电方案的供电方式可分为电缆+直供方式和电缆+AT 供电方式。该供电方式下，牵引电缆可采用二芯电缆或者由2 根单相电缆构成，下文以二芯电缆为例，针对较为复杂的电缆+AT 供电方案展开研究。

根据AT 供电方式的不同，将电缆+AT 供电方式分为电缆+日本AT 供电方式、电缆+法国AT 供电方式和电缆+新型AT 供电方式。分析3种电缆+AT 供电方式时，以电缆+日本AT 供电方式为例分析电缆+AT 供电方式，其同相供电和异相供电方式如图1 所示。图中：T，R 和C 分别为接触网，钢轨和负馈线；SL1，SR1，SR2和ATL1，ATR1，ATR2分别为AT所的编号及对应AT所变压器的编号；SS 为牵引变电所，在其中设置AT 变压器；TC 和NC 及TC1和NC1为两回路牵引电缆，互为备用，每隔一段距离与AT 牵引网通过横向连接线连接，构成电缆牵引网，当一回路TC 和NC故障后，另一回路TC1和NC1投入工作，提高系统的可靠性和可维护性。

当负序超标时，图1（a）供电方式可采用组合式同相供电技术方案［6］和基于SVG 的负序补偿技术方案［12］等；图1（b）供电方式可采用基于SVG 的负序补偿技术方案和铁路功率融通装置补偿技术方案等。

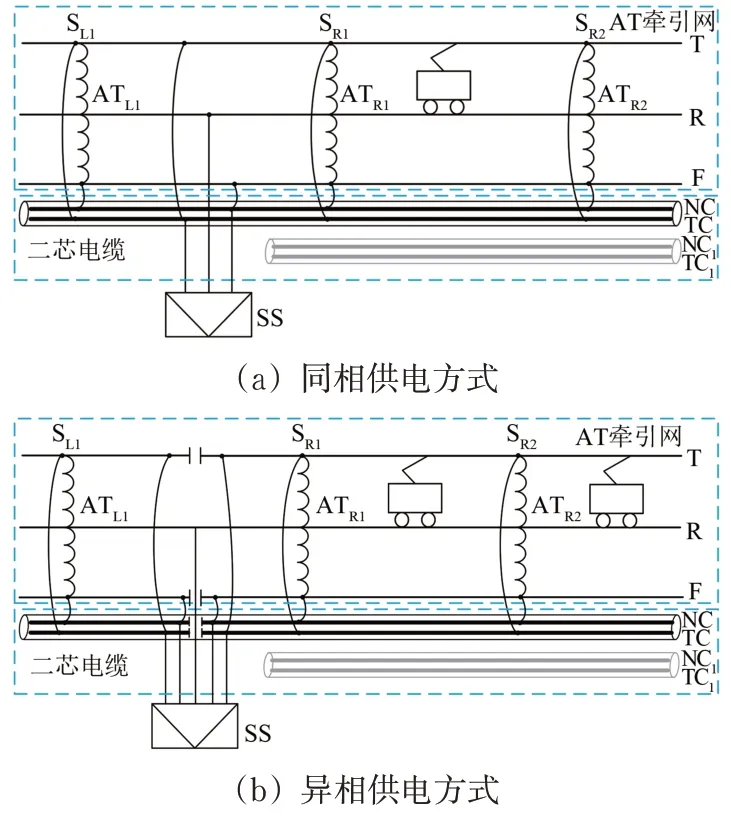
图1 电缆+日本AT供电方式示意图

2 电缆牵引网数学模型

2.1 等值电路模型

以图1 中的右供电臂为例，二者均可描述为图2 所示等值电路。由于二芯电缆中电流幅值相同且相位相反，故可忽略AT 牵引网与二芯电缆之间的互阻抗。将图2 中列车前后两侧AT 变压器及变压器之间的电缆牵引网共同构成的回路定义为短回路；将SS出口处至列车所在短回路中靠近SS出口处的AT 变压器之间的回路定义为长回路。图中：Ic1，Ic3，Ic4和Ic5分别为长回路T 线、F 线、TC线及NC线中流过的电流相量；IT1，IT2，IR1，IR2，IF，ITC和INC分别为短回路相应线路流过的电流相量；U和I分别为列车两端的电压和电流相量；dX为短回路中靠近SS 出口处的AT 变压器距列车的距离；d0为短回路中2 个AT 变压器之间的距离；dL为列车距SS 出口处的距离；2U0为SS 出口处TC与NC之间的电压。

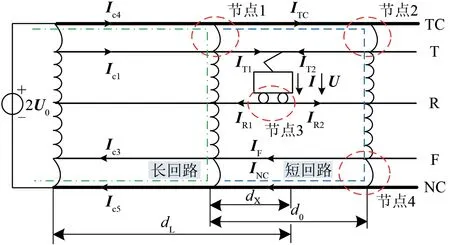
图2 电缆+日本AT供电方式下等值电路

分析电缆牵引网中仅有1 列列车的情形，可得图2中节点1—节点4的电流相量方程为

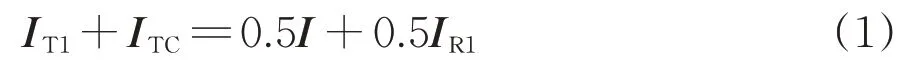
列车所处AT 段中AT 变压器的上绕组和下绕组回路的电压降ΔU和ΔU′分别为

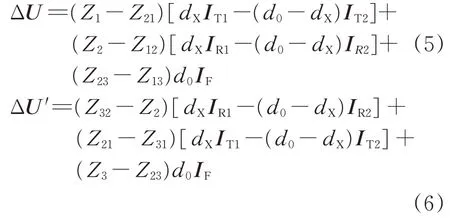
式中：Z1，Z2和Z3分别为电缆牵引网T 线，R 线和F 线的单位长度自阻抗；Z12（Z21），Z13（Z31）和Z23（Z32）分别为电缆牵引网T 线，R 线和F 线间的单位长度互阻抗。

将式（1）—式（6）联立，求得IR1，IR2，IT1，IT2，IF，ITC和INC分别为

其中，

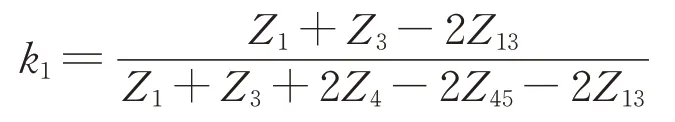
式中：Z4和Z5分别为电缆牵引网TC 线和NC 线的单位长度自阻抗；Z45为电缆牵引网TC 线与NC 线间的单位长度互阻抗。

电缆+法国AT 供电方式和电缆+新型AT 供电方式下第1 个AT 段等值电路如图3 所示，其余AT段等值电路同电缆+日本AT供电方式。

经分析，电缆+法国AT 供电方式下第1 个AT 段电流分布如图3（a）所示，与电缆+日本AT 供电方式相同，则AT 段中各线路电流也完全相同；而电缆+新型AT 供电方式下第1 个电缆AT 段中各线路对应电流I′R，I′TC，I′NC，I′T1，I′T2和I′F分别为

式中：dX1和d1分别为列车位于第1个AT段时对应的dX和d0。

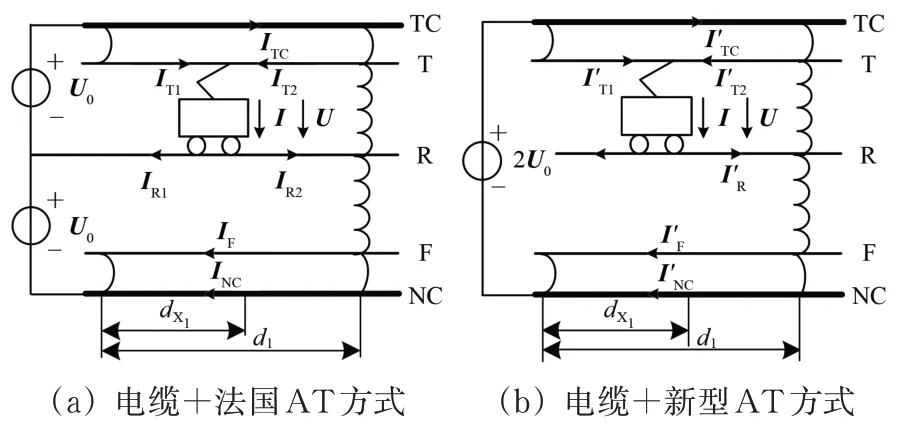
图3 电缆+AT供电方式下第1个AT段等值电路

3 种电缆+AT 供电方式下，SS 出口处至列车处的电压降ΔU1为

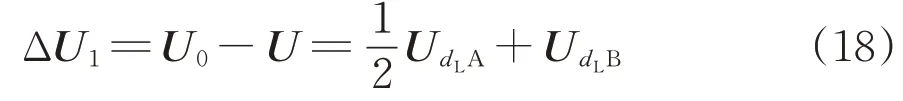
式中：UdLA和UdLB分别为长回路和短回路电压降。

电缆+日本AT 供电方式下，分别对图2 长回路中T 线和F 线及TC 线和NC 线构成的回路列写电压方程，得到UdLA的2种表示方式为

其中，

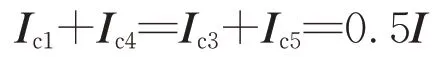
对T 线与钢轨R 构成的回路电压方程，得到UdLB为

将式（18）—式（21）联立，得到单线电缆+AT供电方式电缆牵引网的阻抗Z为

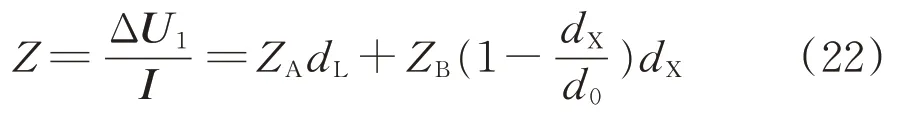
其中，

同理，电缆+法国AT 供电方式下的阻抗Z与电缆+日本AT 供电方式相同；对于电缆+新型AT 供电方式，区别在于第1 个电缆AT 段，其电缆牵引网的阻抗Z′如式（23）所示，其余电缆AT段的阻抗Z与电缆+日本AT供电方式相同。

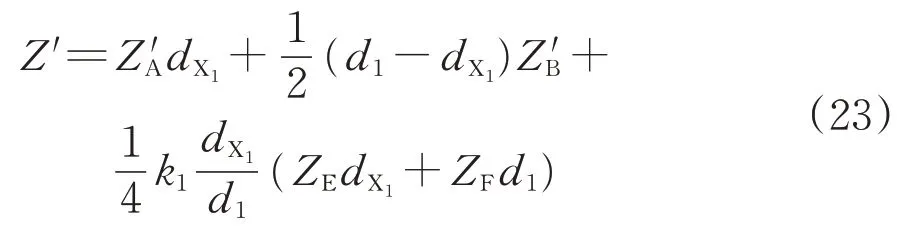
其中，

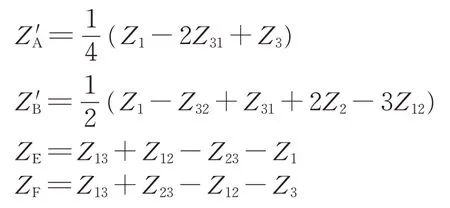
当线路中存在n列列车时，利用叠加原理，得到SS 出口处至列车k（k=1，2，…，n）处的电压降ΔUk为

其中，

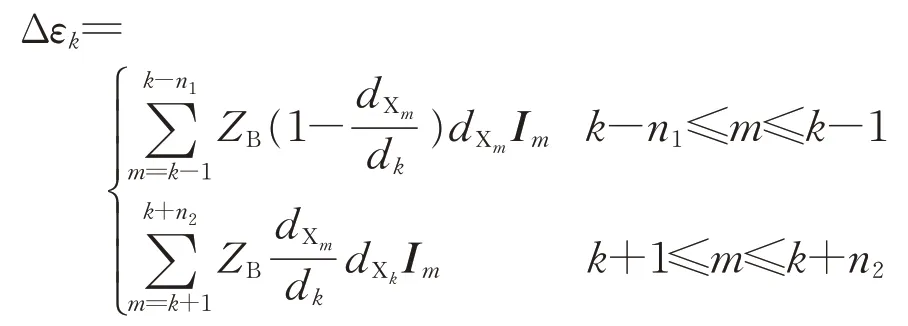
式中：Δεk为短回路中同一AT 段内的其他列车对列车k电压降的影响分量；n1和n2分别为同一AT段内列车k前后两侧列车的数量；Im，In和Ik分别为列车m（m=1，2，…，n），列车n和列车k的电流相量；dk为列车k所处短回路中2 个AT 所之间的距离；dLm和dLk分别为列车m和列车k距SS出口处的距离；dXm和dXk分别为短回路中列车m和列车k与距SS最近AT所间的距离。

根据式（24）得到图4 所示等值电路模型。图中：T′，R′和F′分别为简化后的等效接触网，等效钢轨和等效负馈线，等效负馈线视为理想导线，其中T′和R′的单位长度阻抗分别为ZA和ZB。

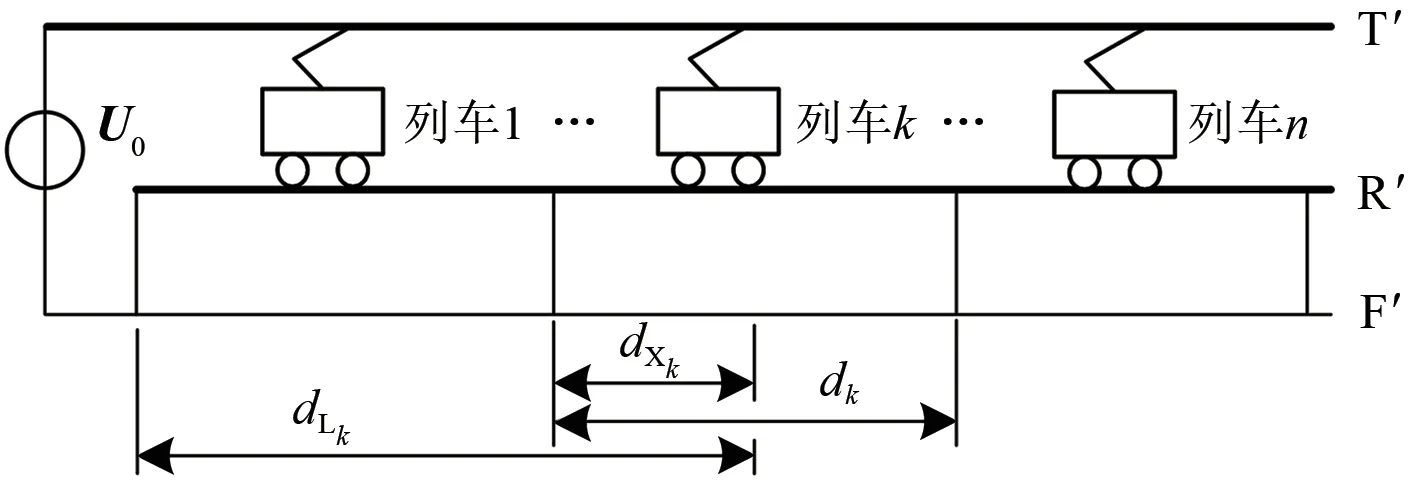
图4 简化后等值电路模型

2.2 链式电路模型

根据供电区间的不同，可以供电臂、牵引变电所或线路全线作为单元进行连续线性潮流计算［13-15］，下文以牵引变电所为单元进行计算，其电缆牵引网链式电路模型如图5所示。图中：ω1为牵引网被划分的切面数；Zω为第ω（1≤ω≤ω1-1）与第ω+1 个切面间串联元件阻抗矩阵；Yω为第ω个切面处的并联元件导纳矩阵；Iω为第ω个切面处的注入电流相量；切面ω=β和ω=β+1 分别为牵引变压器的两个等效端口切面；Zβ为电分相阻抗矩阵。

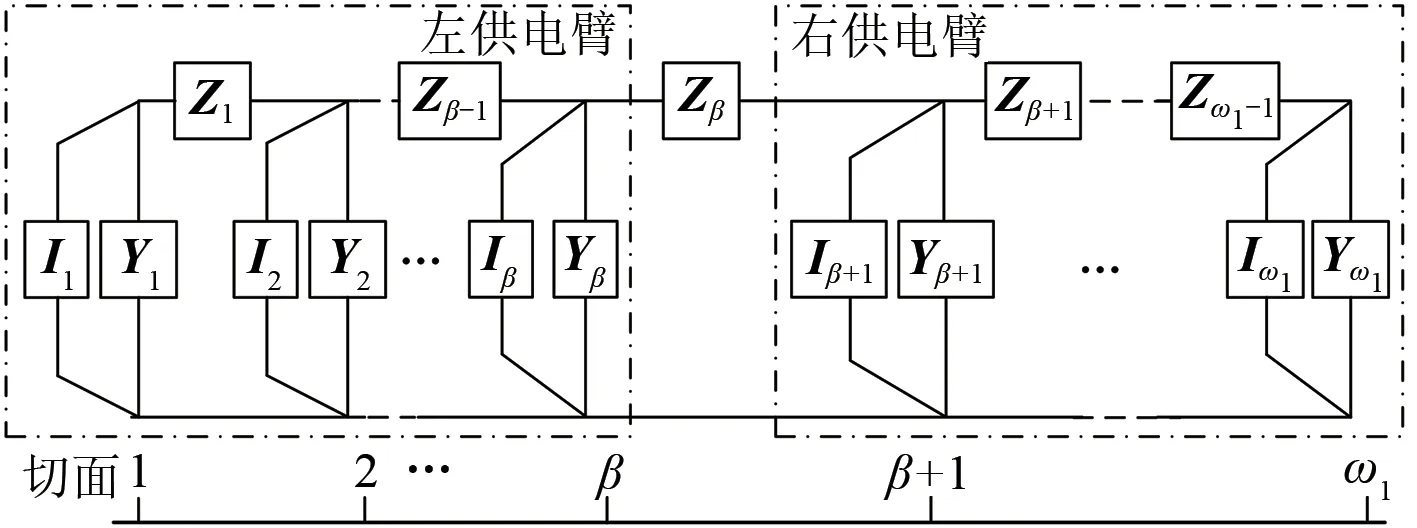
图5 链式电路模型

3 牵引网供电距离

牵引网供电距离直接影响到线路的运输能力，受系统阻抗、负荷大小和补偿方式等因素影响。牵引网电压的合格与否关系牵引网的供电距离。根据式（24）得到n列列车的电压降方程组为

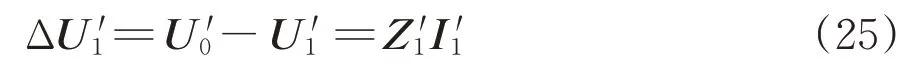
其中，

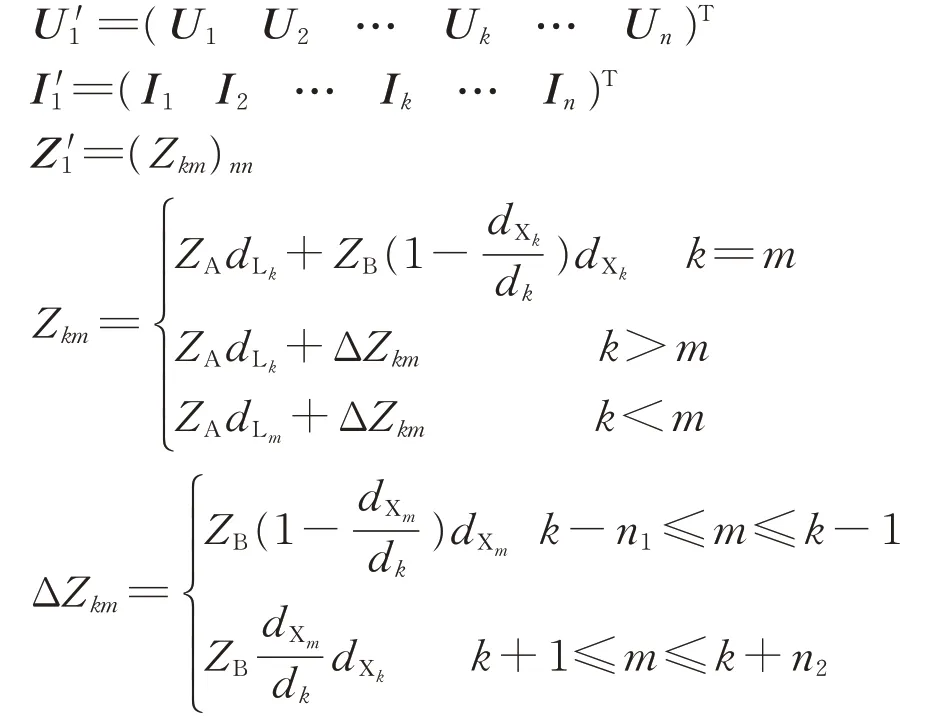
式中：和为SS 出口处电压矩阵和列车端口电压矩阵；为列车电流矩阵；U0k=U0为SS 出口处T 和R 间的电压；为阻抗矩阵；Zkm为中第k行m列的阻抗；ΔZkm为相应的阻抗增量。

令的逆矩阵为=()-1，将式（25）两边均乘，则有

若列车k的复功率为Pk+jQk，将其代入式（26）中得到其潮流方程为

式中：Ykm为中第k行m列的导纳。

将Uk=Uk∠δk，Um=Um∠δm，U0k=U0k∠δ0k，Ykm=Gkm+jBkm，δkm=δk-δm，λk=δk-δ0k代入式（27）中，得到极坐标下的潮流方程为

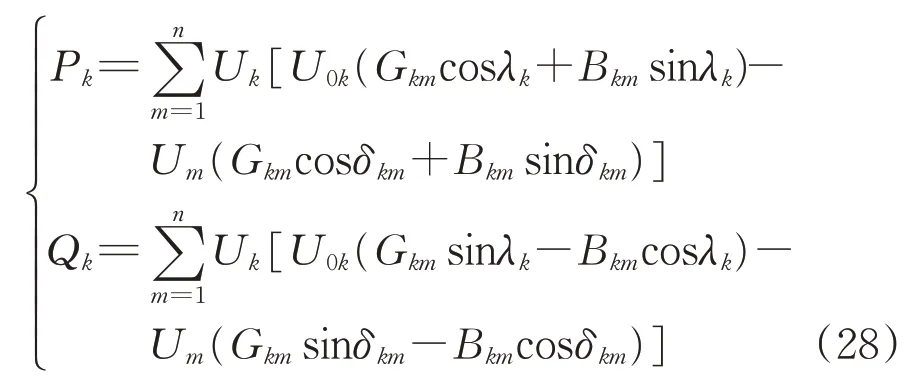
式中：Uk，δk，Um和δm分别为列车k和列车m对应电压的幅值和相角；U0k和δ0k为端口电压的幅值和相角；Gkm和Bkm分别为Ykm中的电导和电纳。

根据式（28），利用牛顿拉夫逊法得到Pk和Qk修正方程的矩阵形式为

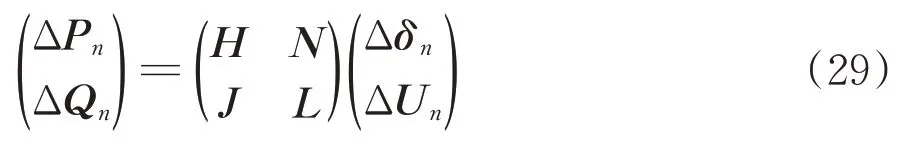
其中，

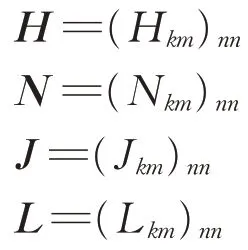
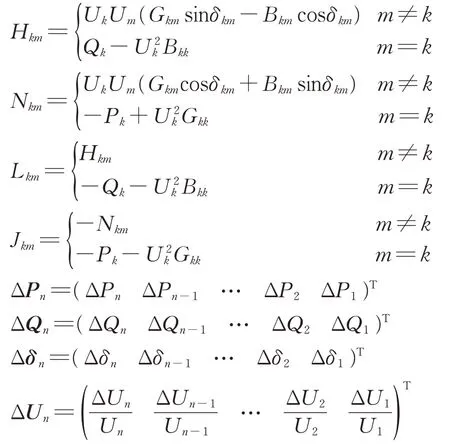
式中：ΔPk，ΔQk，Δδk和ΔUk分别为列车k处有功功率，无功功率，电压相角和幅值的修正量；ΔPn，ΔQn，Δδn和ΔUn分别为列车k处有功功率，无功功率，电压相角和幅值的修正量矩阵；Hkm，Nkm，Jkm和Lkm为雅克比矩阵元素；H，N，J和L为雅克比矩阵元素的矩阵形式。

高铁列车的电压模值|Uk|满足|Uk|∈［20，29］kV［16］，获取列车的负荷过程，按照一定的发车时间间隔或者发车间距，更新线路中列车的位置，根据式（29）求得列车端口的电压，该电压的最小值不低于要求的最低电压，即可得到电缆牵引网的最远供电距离。从运行图出发，以发车间隔T为例，得到确定电缆牵引网供电距离的计算流程。

（1）确定发车间隔T，设定时刻t初值为0，以供电臂端口为起点位置，获取列车的负荷过程数据（即t时刻列车的位置l（t）及复功率P（t）+jQ（t））。

（3）确定牵引网供电方式，计算牵引网的阻抗数据，根据式（22）确定等值阻抗ZA和ZB的取值。根据式（25）确定阻抗矩阵。

（4）根据式（29）进行潮流计算，确定各列车端口电压取值，具体步骤为：

①设定SS 出口处的电压及列车k两端电压的幅值和相角的初值和。

②令迭代次数为p，第p次迭代时列车两端电压的幅值和相角分别为和，第p=1 次迭代时取值为和。

③根据式（28）求得第p次迭代时ΔPk和ΔQk的取值，根据式（29）确定雅克比矩阵，进而求解得到Δδn和ΔUn。

④更新各列车端口电压幅值和相角的新值。

⑤设定电压幅值和相角的收敛精度分别为εU和εδ，判断计算结果是否收敛，若|ΔUk|＜εU，|Δδk|＜εδ，则转至步骤（5）；若不满足，则进行第p+1次迭代，转至步骤③。

（5）判断列车的电压是否满足要求，即|Uk|∈[20，29]kV，校验系统的供电能力，此时可按照每一列列车的最小电压大于20 kV 或者大于22.5 kV 考虑，若满足要求，则进行下1 s 计算，转至步骤（2）；反之，转至步骤（6）。

（6）结束。确定出电缆牵引网单供电臂的最远供电距离。

4 仿真分析

4.1 电缆牵引网阻抗模值

在AT 供电方式下牵引网线路的基础上增加二芯电缆，仿真电缆+AT 供电方式下长距离方案。二芯电缆截面积以300 mm2为例，根据AT 供电方式的不同，可以构成3 种电缆+AT 供电方案。以单线为例，不计保护线的影响，外部电源电压等级为220 kV，承力索型号为JTMH-120，接触线型号为CTMH-150，钢轨型号为P60，负馈线型号为LGJ-185，分析上行线路的牵引网等值阻抗，计算得到3种电缆+AT供电方式及3种AT供电方式下距SS 出口处距离lkm 处的牵引网等值阻抗模值如图6所示。

图6 不同供电方式下牵引网等值阻抗模值

由图6可知：从第2个电缆AT段开始，3种电缆+AT 供电方式的牵引网等值阻抗模值变化趋势与AT 供电方式相同，均呈马鞍形，且电缆+AT供电方式的牵引网等值阻抗较AT 供电方式更小；电缆+日本AT 供电方式的牵引网等值阻抗模值与电缆+法国AT 供电方式一致；电缆+新型AT 供电方式的牵引网等值阻抗模值与电缆+日本（法国）AT 供电方式的区别在于第1 个电缆AT 供电段，其余电缆AT 段牵引网等值阻抗模值曲线与电缆+日本（法国）AT供电方式一致。

以日本AT 供电方式和电缆+日本AT 供电方式为例，分析相邻AT 所间的距离对牵引网等值阻抗模值的影响。设定日本AT 供电方式的AT 所的距离为10 km，电缆+日本AT 供电方式的AT 所间的距离分别为10，11，12和13 km，不同供电方式下的牵引网等值阻抗模值计算结果如图7 所示。由图7 可知：电缆+AT 供电方式下，一定范围内相邻AT 所间的距离越大，短回路的牵引网等值阻抗模值最大值则越大；相较日本AT 供电方式，电缆+AT 供电方式下的牵引网等值阻抗模值更小，则相邻AT所间的距离可以设置更长。

图7 不同相邻AT所间距离时牵引网等值阻抗模值

4.2 电缆牵引网供电距离

设定列车速度为250 km·h-1，列车功率分别为9.6 和19.6 MW，列车功率因数均为0.98，AT所间的距离均为12 km。以日本AT 供电方式和电缆+日本AT 供电方式为例，分析电缆牵引网供电距离。根据小节3 内容分别计算SS 出口处电压分别为27.5 和25.0 kV 情形下列车发车间隔分别为6，7和8 min时2种供电方式下的牵引网供电距离。

以6 min 发车间隔为例，电缆牵引网供电距离计算结果如图8 所示，图中限值1 为22.5 kV，指列车的最低正常工作电压，限值2 为20.0 kV，指列车的最低工作电压。电缆牵引网最长供电距离统计结果见表1。由表1 可知，相同牵引负荷下，电缆+AT 供电方式电缆牵引网的供电距离约是AT供电方式的2.5倍。

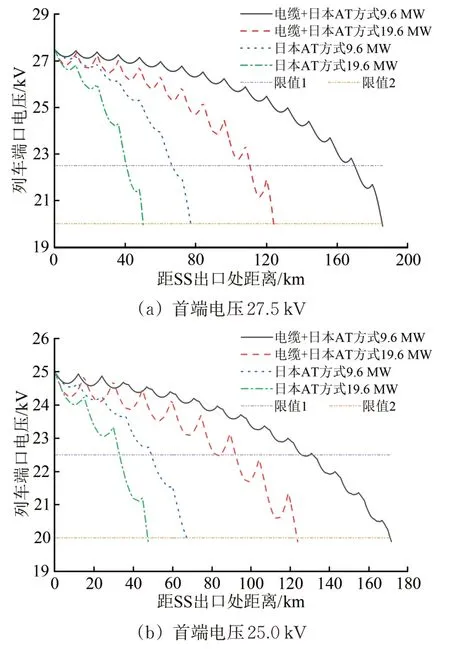
图8 不同供电方式下6 min 发车间隔时的电缆牵引网供电距离

表1 不同供电方式和发车间隔下电缆牵引网最长供电距离

设定列车功率为9.6 MW，列车最低正常工作电压为22.5 kV，发车间隔为6 min，其余参数不变，分析2 种供电方式下相邻AT 所距离分别为12，13，14，15 和16 km 时的牵引网最长供电距离，计算结果见表2。

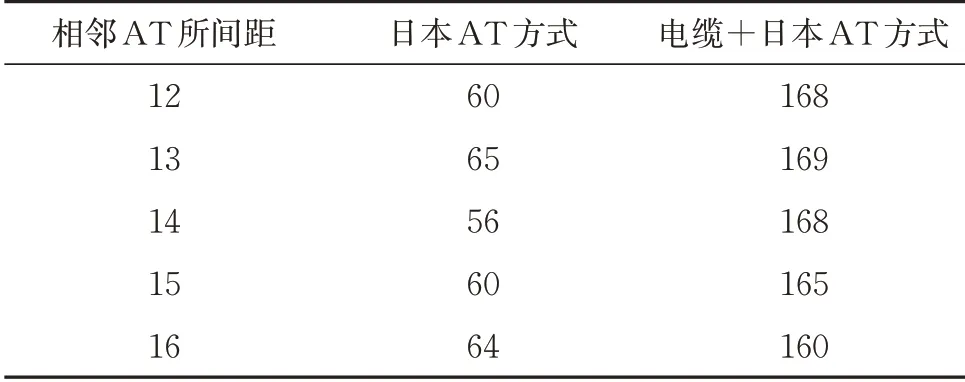
表2 不同AT所间距下的牵引网最长供电距离 km

由表2 可知，不同AT 所间距下的牵引网最长供电距离，电缆+AT 供电方式约是日本AT 供电方式的2.5 倍。因此，采用电缆+AT 供电方式，可以增加相邻AT所之间的距离。

4.3 实例计算

以某复线全并联AT 供电线路为例，外部电源和牵引网参数设定同4.1，列车型号为CRH380A，功率因数为0.98，该线路长度为145.15 km，既有供电方案为AT 供电3 所方案，如图9（a）所示。图中：A3，A7 和A11 为牵引变电所；A1，A5，A9和A13为分区所；其余为AT所。按照第3节所述方法，确定单个供电臂的供电距离，则可以得到3个电缆+AT供电方案，电缆+AT供电方案可采用同相供电也可采用异相供电，分为电缆+AT 供电3所方案、电缆+AT 供电2 所方案（如图9（b）所示）和电缆+AT 供电1 所方案（如图9（c）所示），电缆+AT供电3所方案的牵引变电所分布与AT 供电3 所方案相同。图9（b）中B2 为分区所，B1和B3为AT 所，其余设定不变；图9（c）中C2和C4 为牵引变电所，二者互为备用，C1，C3 和C5为AT所，其余设定不变。

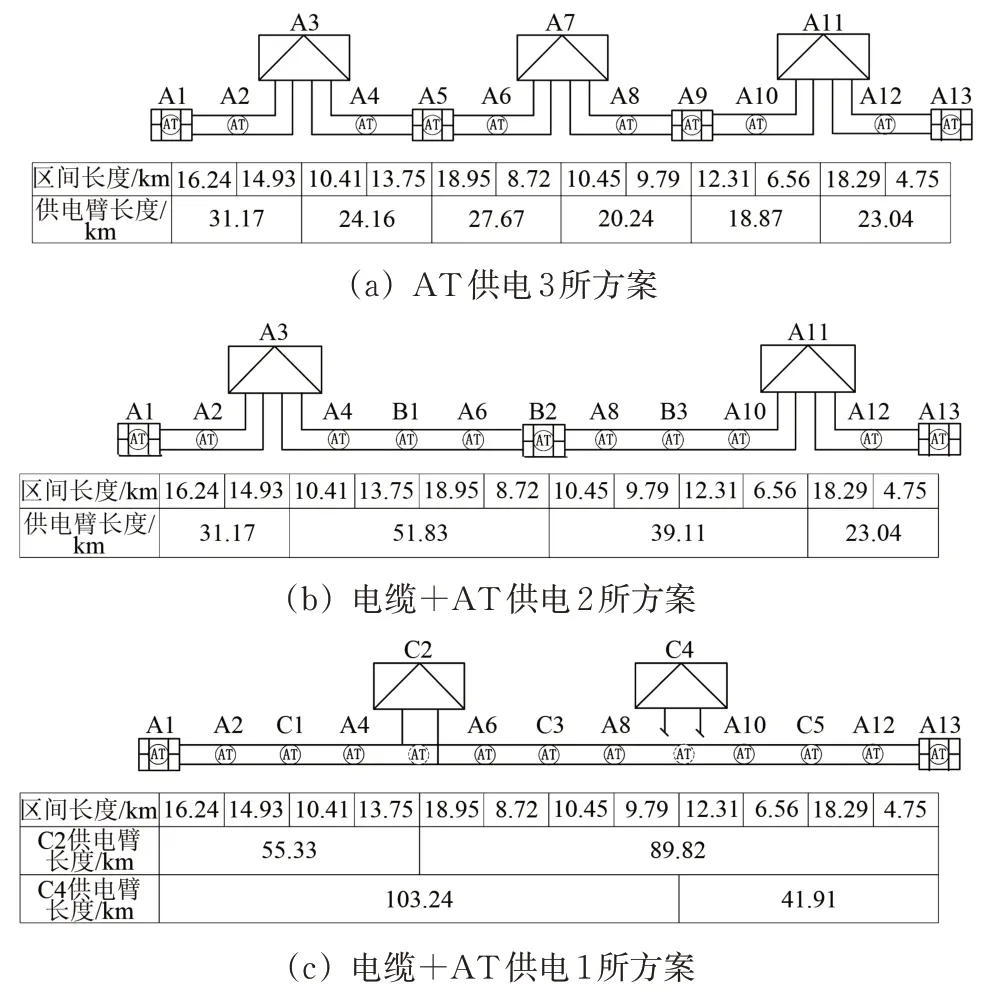
图9 不同供电方案时供电区间分布

为确保线路运营裕度，远期和近期最小发车间隔分别为4 和5 min。2 种发车间隔下4 个方案不同位置处的牵引网最低电压分别如图10和图11所示。

对图10 和图11 所示4 个供电方案的全线最低牵引网电压进行统计，结果见表3。由表3 可知：电缆+AT 供电方式的1 所方案牵引网最低电压最低，但大于22.5 kV，列车仍可正常工作；电缆+AT 供电方式的3 所和2 所方案的牵引网最低电压均大于AT 供电3 所方案，满足列车正常工作电压要求；虽然4个供电方案都可行，但考虑到减少电分相和外部电源的数目，可考虑采用电缆+AT 供电的1所同相供电方案或者2所同相供电方案。

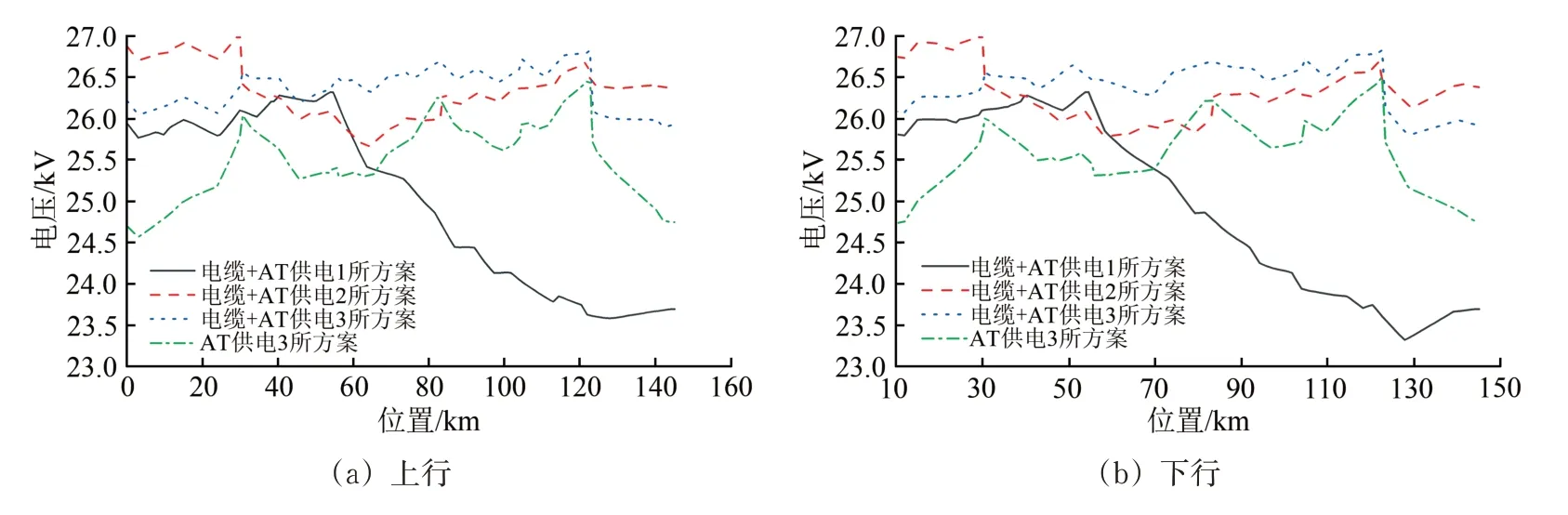
图10 远期4 min发车间隔牵引网最低网压分布

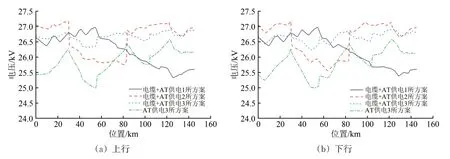
图11 近期5 min发车间隔牵引网最低网压分布

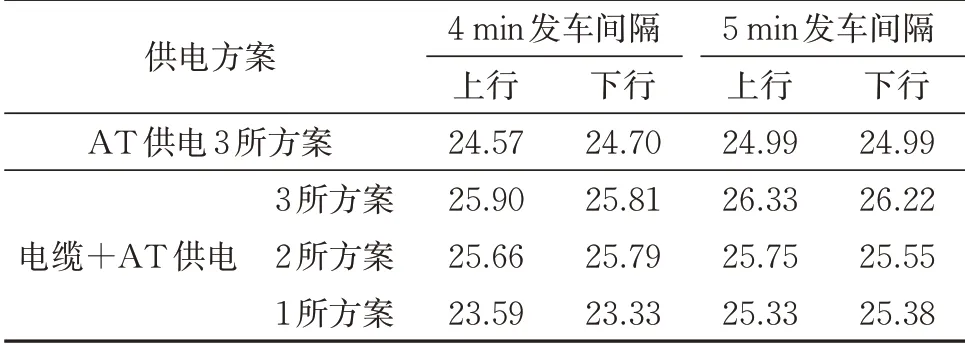
表3 全线电缆牵引网最低电压 kV

5 结 语

电缆牵引网长距离供电方案的供电方式包括电缆+直供方式和电缆+AT 供电方式，重点以电缆+AT 供电方式为例，从不同角度对其进行了研究。以列车工作电压为约束条件，基于多列列车负荷的潮流计算模型，提出了确定电缆牵引网供电距离的方法。分别对电缆牵引网阻抗和供电距离等进行仿真分析，并以某线路为例进行方案设计与对比，结果表明电缆+AT 供电方案牵引网等值阻抗更小；电缆+AT 供电方式供电距离约是AT 供电方式的2.5 倍，有效提高了供电距离，能够增加外部电源选址的灵活性。

本文所述模型对于电缆+直供方式仍适用，所述方案对于市域铁路、重载铁路、长大坡道线路等线路的新建线和既有线均适用；若与新型供电方式和新技术进行进一步结合，可以进一步提升牵引供电系统的供电距离。