改进小波阈值在心电信号去噪中的应用

檀雪 ，叶继伦 , ，张旭 ,，李晨洋，周晶晶，窦可建

1 深圳大学 生物医学工程学院，深圳市，518060

2 深圳市生物医学工程重点实验室，深圳市，518060

3 广东省生物医学信号检测与超声成像重点实验室，深圳市，518060

0 引言

心电信号是一种微弱的微生物信号，频率范围主要在0.05 Hz到100 Hz之间[1-2]，容易受到外界高频噪声的干扰且波动较大，由于大部分噪声会和心电信号叠加在一起，使得纯净的心电信号产生畸变，导致心电图中包含的信息不能真实地反应心脏变化情况，同时也对后续的心电信号特征点的提取形成干扰，所以对心电信号进行降噪处理十分必要。在工程中，一般选用小波阈值去噪法，由于噪声和纯净的心电信号的能量分布不相同，将含噪的心电信号经过小波变换后，心电信号能量主要分布在较大的小波系数中，而噪声不会集中分布，所以两者在小波系数上的幅值是不一样的，随后采用阈值法降噪可以有效地将噪声和心电信号进行分离[3]。但是DONOHO等[4-5]提出的传统的软硬阈值降噪法分别存在估计的小波系数与真实小波系数具有偏差，重构信号时误差较大，和在临界阈值处的不连续导致信号失真等缺点。

针对传统软硬阈值的优缺点，提出一种改进的阈值函数，克服了原有的不足，并且通过仿真分析与数据检验，验证了改进阈值函数的降噪算法的高效性和优越性。

1 小波阈值去噪

1.1 阈值去噪原理

假设采集到的心电信号表现形式见式(1):

其中x(t)为纯净的心电信号，G(t)表示含有噪声的心电信号，r(t)表示噪声。对心电信号进行小波去噪的基本流程，如图1所示。

图1 小波去噪流程Fig.1 Wavelet denoising process

首先选择合适的小波基和分解层数对含噪的心电信号进行小波变换，得到各分解层对应的小波系数，包括纯净信号的小波系数和噪声信号的小波系数，且前者的值比后者大；再选用合适的门限阈值和阈值函数，对各层小波系数进行量化；最后对量化后的小波系数进行重构，从而得到去噪后的心电信号。

1.2 阈值函数

小波阈值函数是能否对心电信号高效进行去噪的关键，选择一个合适的阈值可以提高去噪质量，提高信号诊断的精确度。阈值过大，可能导致信号过于平滑，滤掉信号的细节分量；阈值过小，滤波效果较差，仍存在较多的噪声。传统的阈值函数为DONOHO等[4-5]提出的软阈值和硬阈值。

（1）硬阈值函数

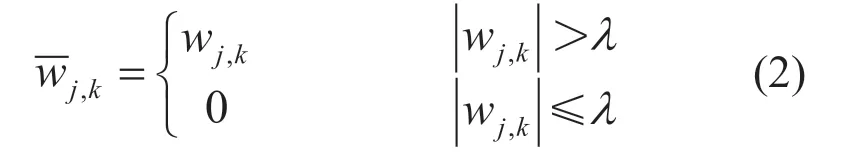
（2）软阈值函数

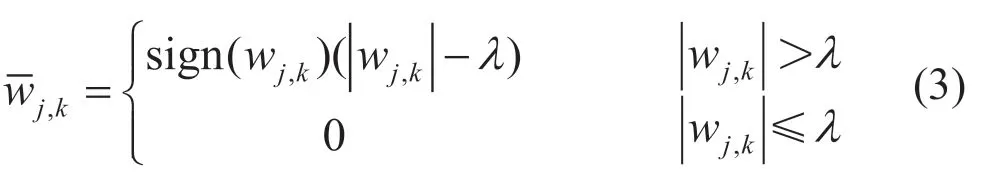
除了传统的软硬阈值函数外，研究学者在此基础上做出改进，例如吴安全[9]提出的半软阈值函数，GAO[10]提出的Garrote函数。

（1）半软阈值函数[9]

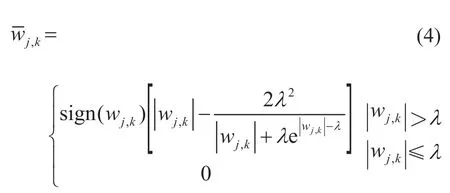
在小波系数小于临界阈值情况下与传统的硬阈值函数一样，直接置零；当小波系数大于临界阈值的情况下，小波系数收缩。

（2）Garrote函数[10]

（3）本研究算法

在以上所述的阈值函数基础上提出一种改进的阈值函数：

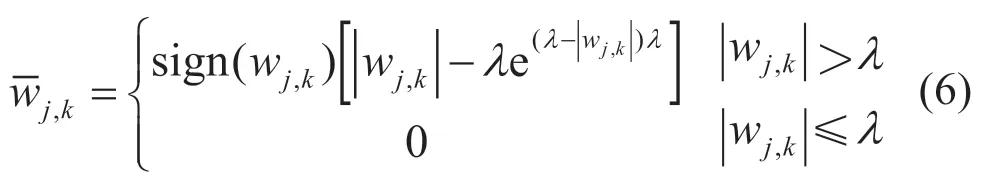
所提出的改进的阈值函数在临时阈值处是连续的，可以解决上述软硬阈值的缺点。

2 改进阈值函数分析

2.1 改进阈值函数理论证明

（1）证明阈值函数的连续性：

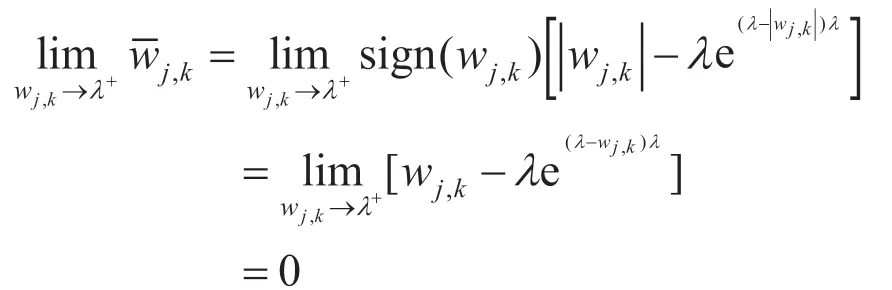
且当wj,k→λ-时即函数在λ处具有连续性，同理当wj,k→-λ-时：即函数在-λ处具有连续性，即改进的阈值函数在±λ处都具有连续性，可以克服硬阈值函数在临界阈值处的不连续性。

（2）证明阈值函数的偏差性：

当wj,k→+∞时：

（3）改进阈值函数的渐近性：

当wj,k→+∞时：

2.2 不同阈值函数曲线对比

将传统的硬阈值函数和软阈值函数以及改进的阈值函数放在同一坐标系下做出曲线图进行对比分析。几种阈值函数进行曲线对比，如图2所示。

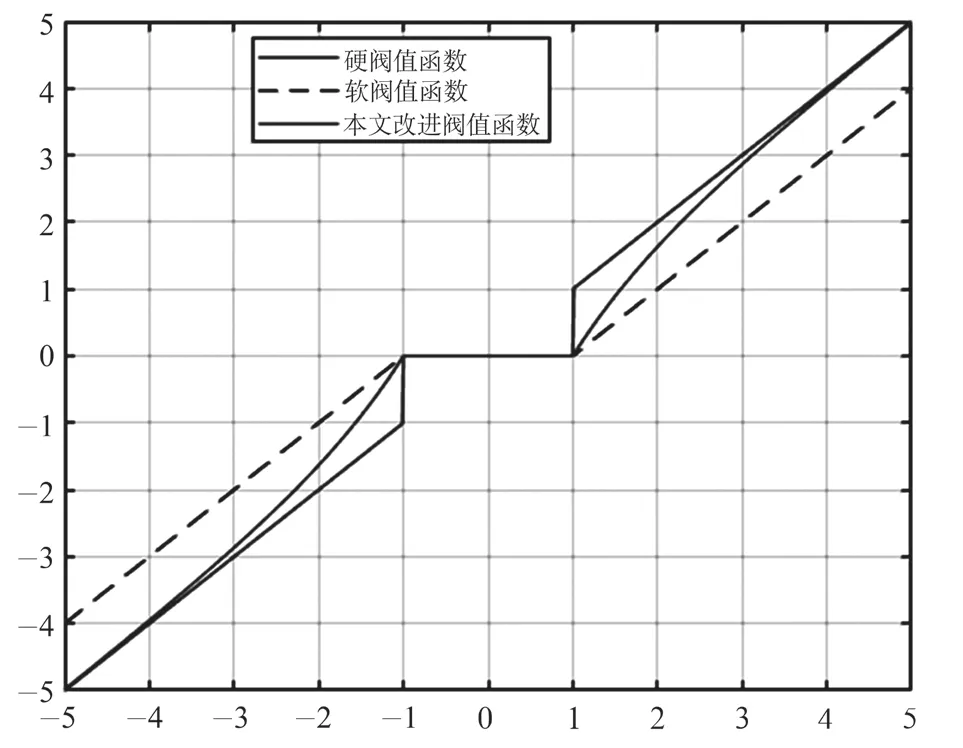
图2 几种阈值函数进行曲线对比Fig.2 Several threshold functions were compared

改进的阈值函数曲线图在硬阈值函数和软阈值函数曲线之间，改善了传统阈值函数带来的不连续问题和固定偏差问题，使得重构的小波信号更加贴合真实信号，可再次证明改进的阈值函数优于传统的阈值函数。

3 实验仿真结果与分析

3.1 仿真性能衡量指标

为了比较不同阈值函数的降噪效果，一般采用信噪比(SNR)和均方差(MSE)作为衡量指标[11]，信噪比越高代表去噪的效果越好，均方差越低表示去噪的质量越理想。定义分别为：

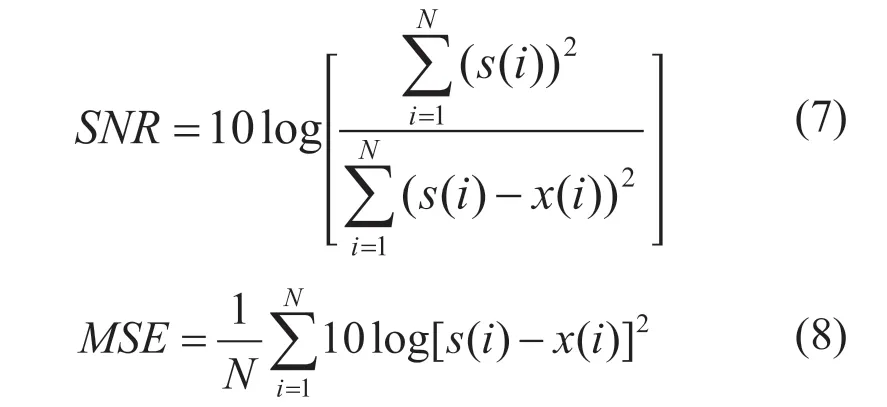
其中s(i)代表含噪信号，x(i)代表经过小波去噪后的信号，N表示信号的总长。

3.2 实验结果与分析

为了证明改进阈值函数降噪效果的有效性，使用美国麻省理工心电数据库(MIH-BIH Arrhythmia Database)中的100号心电信号作为纯净的信号，对其分别加入4 db、6 db、8 db、10 db的高斯白噪声，如图3所示。

图3 不同信噪比的噪声信号Fig.3 Noise signals with different SNR

将加入10 db高斯白噪声，分别用原始的硬阈值、软阈值、文献[9]提出的半软阈值和所提出的改进阈值函数进行去噪，对比效果，如图4所示。图4表明传统的软硬阈值以及改进阈值函数降噪效果较明显，文献[9]方法基本不适应，达不到理想的降噪效果。

图4 几种阈值函数降噪效果对比Fig.4 Comparison of noise reduction effects of several threshold functions

同时通过仿真实验得出降噪效果衡量指标信噪比(SNR)与均方差(MSE)，如表1所示。可以看出改进的阈值函数的小波去噪的SNR相对于另外三种阈值函数最大，MSE均比其他三种算法小，则表示改进的阈值函数去噪效果较好。

表1 不同阈值函数降噪性能比较Tab.1 Comparison of noise reduction performance of different threshold functions

最后计算含有不同信噪比的心电信号的降噪后信噪比(SNR)与均方差(MSE)，做出曲线对比图，从图中曲线可知对含有不同信噪比高斯噪声的信号进行降噪，所提算法在SNR和MSE上都具有优势，降噪效果较好。输出SNR、MSE效果对比曲线，如图5所示。

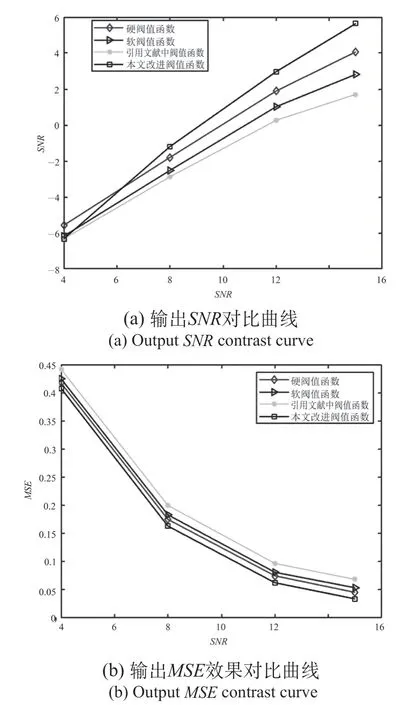
图5 输出SNR, MSE效果对比曲线Fig.5 Comparison curve of output SNR and MSE effect

4 总结

笔者研究的是含噪的心电信号经过小波阈值去噪滤除信号中的噪声的方法，考虑到传统的软硬阈值去噪具有平滑性和偏差性上的不足，提出了一种改进的小波阈值函数，通过理论证明和实验分析确定了改进的阈值函数，该函数保留了传统阈值方法的优点，同时也解决了不连续和信号偏差问题，在对SNR和MSE的判定上也表明所提算法去噪效果高于其他阈值函数，充分体现了改进阈值函数的高效可靠性。