自生固相化学压裂缝内温度分布数值模拟

罗志锋，张楠林，赵立强，鲜 超，王春雷，庞 琴

（1.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都610500；2.中国石油塔里木油田分公司天然气事业部井下作业部，新疆库尔勒841000；3.中国石油玉门油田分公司勘探开发研究院，甘肃酒泉735000）

自生固相化学压裂是利用不混相的两种流体（分别被称为相变压裂液、非相变压裂液）压开并形成一定几何尺寸的人工裂缝，在地层温度的作用下，相变压裂液经过相变转变为固相颗粒，达到支撑水力裂缝的目的，而非相变压裂液占据裂缝中一定空间，施工结束返排，让出的空间作为油气流动通道，从而形成具有高导流能力的人工裂缝[1-7]。在自生固相化学压裂中形成固相颗粒的控制条件是缝内温度。另外，不同温度下压裂液体系具有不同的黏度值，压裂液体系黏度直接关系到裂缝几何尺寸，裂缝几何尺寸又是计算裂缝温度分布的必要条件，三者之间相互影响。所以温度是该项技术最重要、最基础的影响因素。自1967年Dysart和Whitsitt[8]根据能量守恒建立了缝内温度变化方程并推导出任意时刻、任意位置处裂缝流体温度的解析式以来，压裂过程中裂缝温度场的研究就进入蓬勃发展期[9]，其中最具有代表性的有：1969年，Wheeler[10]在考虑滤失速度为常数且缝宽为定值的条件下，提出了一种解析模型，但表达式较复杂，难以应用；1984年，Biot 等[11]运用变分法原理推导了一种计算壁面热流量的热流函数，提出了裂缝温度场的一种数值计算模型，该模型假设的线性温度变化规律不太合理，适用范围受限；20 世纪90年代，Kamphuis 等[12]根据物质和能量守恒推导了裂缝、滤失带和油层温度分布式，采用差分法进行求解，模型考虑了缝中流体与岩石壁面间的温度差，较为完善；罗攀登等考虑径向非稳态传热、轴向非稳态对流以及摩擦力、黏滞力的影响，推导出井筒温度、压力方程，结合KDR 方法和CO2物性模型，建立了CO2压裂过程中井筒和裂缝温度场计算模型[13]。上述模型大多是建立在二维解析裂缝模型的基础上计算缝内温度场的，不能准确模拟压裂过程中水力裂缝内温度分布，所以，乔继彤等[14]考虑了压裂液的热传导、热对流和热耗散以及压裂液与岩石之间的热交换，耦合了传热方程和水力压裂三维裂缝扩展模型；Kresse 等[15]耦合传热模型和UFM模型，对体积压裂裂缝温度场进行了模拟研究。在热流固耦合方面：Sun 等[16]利用局部热不平衡理论，建立了耦合的三维数值模型，研究增强地热系统中复杂裂缝内温度分布规律；孙可明等建立了考虑热对流和热传导效应的热流固耦合力学模型，研究高温岩体储留层注水过程中缝网间距对储留层岩体温度的影响规律[17]。

从国内外水力裂缝温度场的研究成果来看，裂缝温度场的计算由二维裂缝延伸模型逐渐发展为以三维裂缝延伸模型为基础，从裂缝延伸模型和裂缝传热模型分开计算逐渐发展为耦合计算。

自生固相化学压裂过程中裂缝扩展与缝内传热同时进行，相互影响，同时，由于自生固相化学压裂使用的两种流体热力学参数不完全一致，现有模型不能准确反映受两种流体体积比影响的温度场分布。基于能量守恒原理，结合均相流模型[18]，建立缝内流体传热方程，并与拟三维裂缝模型进行耦合[19]，构建自生固相化学压裂拟三维裂缝温度场模型，同时引入了温度对相变压裂液、非相变压裂液黏度的影响，准确反映出在压裂液体系黏度变化下的裂缝几何尺寸。通过实例计算和分析，研究自生固相化学压裂缝内温度场的变化规律。

1 缝内温度分布数学模型

1.1 拟三维裂缝扩展模型

压裂液传热是在裂缝中进行的，通过对拟三维裂缝几何尺寸模型的推导及求解，为后面的压裂液传热模拟提供动态的裂缝几何尺寸，能更合理地计算裂缝温度场。应力对称下的裂缝延伸拟三维控制方程为[19]：

流体滤失量vl可按下式计算[20]：

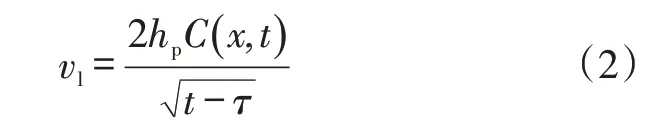
式（1）—式（2）中：q(x,t)为t时刻缝内x处的流量，m3/s；x为缝长方向位置，m；vl(x,t)为t时刻缝内x处流体滤失量，m2/s；A(x,t)为t时刻缝内x处裂缝横截面积，m2；t为施工时间，s；hp为裂缝高度，m；C(x,t)为t时刻缝内x处流体滤失系数，m/s0.5；τ为流体到达裂缝x处的时间，s。

简化的缝中流体压降方程[21]：

式中：p(x,0,t)为t时刻裂缝中x处的压力，MPa；μf为压裂液黏度，mPa·s；h(x,t)为裂缝中x处的缝高，m；wf(x,0,t)为t时刻裂缝中x处半裂缝宽度，m。

裂缝宽度方程[9]：

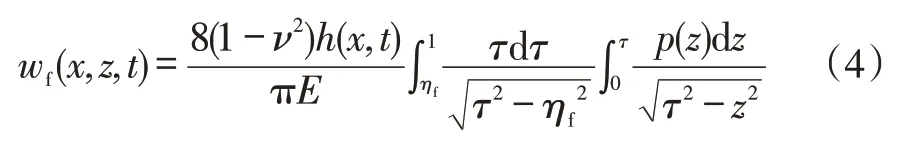
式中：wf(x,z,t)为缝长x 缝高z处的裂缝宽度，m；z为缝高方向位置，m；ν为泊松比；E为弹性模量，MPa；p(z)为缝高位置z处的净压力，MPa。

裂缝高度方程[19]：

式中：H为裂缝半高，m；Kc为应力强度因子，MPa·m0.5；Δs为应力差，MPa；f为油层厚度与裂缝高度之比。

1.2 裂缝传热模型

图1为自生固相化学压裂温度场物理模型，裂缝中充满两种非混相流体，分别为相变压裂液（流体1）、非相变压裂液（流体2），两种流体存在流体界面。Tin为注入流体的温度，u为注入速度，Ti为裂缝中温度，Tres为原始地层温度。假设地层岩石的热物理性质不随时间和温度发生变化，只考虑垂直缝壁方向上的热交换，忽略缝长方向上的热交换。

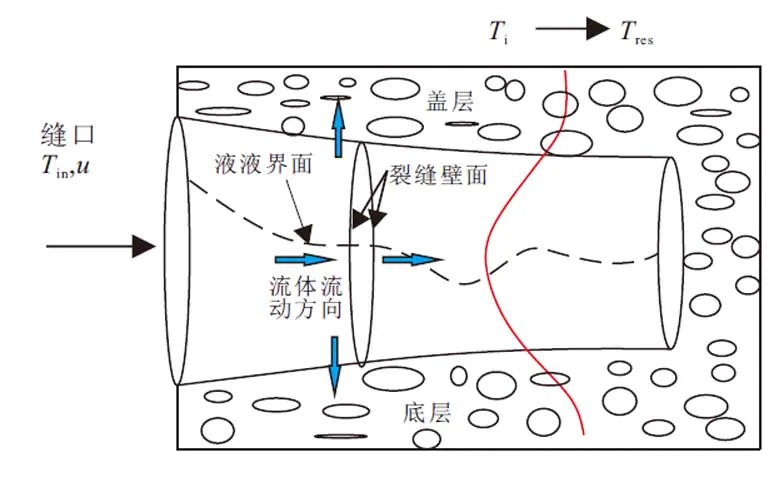
图1 自生固相化学压裂温度场物理模型Fig.1 Physical model of temperature field for in-situ generated proppant fracturing

裂缝内压裂液的流动伴随着动态的传质、传热过程，裂缝壁面上缝内流体滤失进入地层，同时热量向缝内传递。

缝中液体能量方程[22]：

与现有压裂温度场模型不同的是，常规模型都是只考虑单一流体的热交换，而在该文中，相变压裂液体系由相变压裂液、非相变压裂液组成，其热力学参数取二者的加权平均值：

式（6）—式（7）中：Tf为缝中液体温度，℃；v为缝中液体流速，m/s；α为换热系数，J/（m2·s）；w为裂缝平均宽度，m；Trw为裂缝壁面温度，℃；ρ1、ρ2分别为相变压裂液、非相变压裂液密度，kg/m3；C1、C2分别为相变压裂液、非相变压裂液比热容，J/（kg·K）；f1、f2分别为相变压裂液、非相变压裂液体积分数。

由于压裂过程中热对流作用大于热传导，可忽略缝长、缝高方向的热传导。

滤失带能量方程[23]：

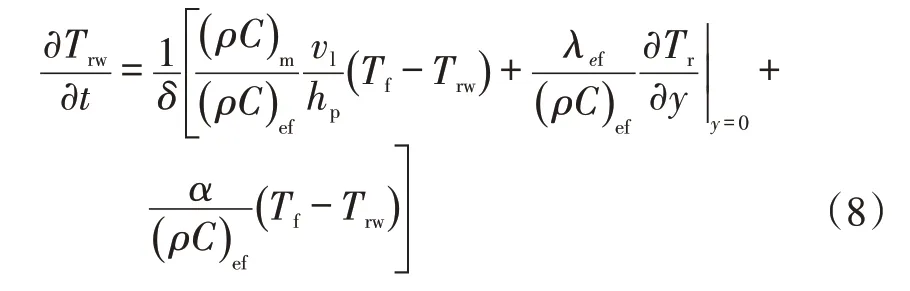
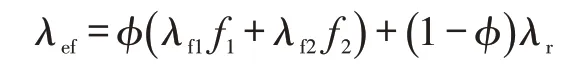
式中：δ为滤失带深度，m；φ为储层平均孔隙度；ρr为储层岩石密度，kg/m3；Cr为储层岩石比热容，J/（kg·K）；λf1、λf2分别为两种压裂液的热传导系数，W/（m·K）；λr为岩石的热传导系数，W/（m·K）；Tr为储层岩石温度，℃。

岩石能量方程[22]：

1.3 初始条件和边界条件

压裂前裂缝内各点的温度为原始地层温度。在化学压裂过程中，注入排量恒定，裂缝顶部和底部（即y=0和y=h处）无压裂液流动，裂缝出口端的压力为地层压力，裂缝入口端的压裂液温度为井底压裂液的温度。

1）初始条件

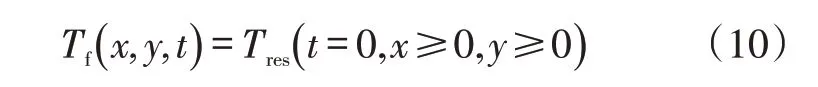
式中：Tres为原始地层温度，℃。

2）边界条件

式中：qin为缝口注入排量，m3/min；Twf为井底处压裂液体系的温度，℃。

1.4 模型求解

建立的拟三维裂缝延伸模型由连续性方程、压降方程、裂缝宽度方程及裂缝高度方程组成，4个主体方程相互影响，不能直接求出解析解，需结合边界条件，采用适当的迭代算法进行求解，在每一时间步计算出裂缝几何尺寸后，利用温度场差分离散的数值方程求解温度分布，更新流体黏度，再进行下一步的计算，直到施工结束，计算流程见图2。

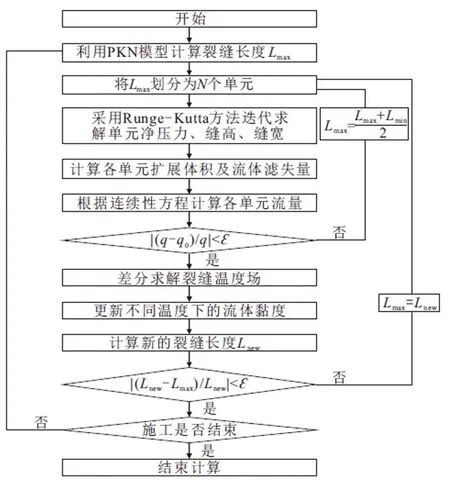
图2 缝内温度分布数学模型求解流程（Lmin为前一时间步裂缝长度）Fig.2 Mathematical model solving process of temperature distribution（Lmin is the length of fracture in previous step）

对裂缝内液体能量方程（6）进行差分离散：

对滤失带能量方程（7）进行差分离散：

对近缝带岩石能量方程（8）进行差分离散：

式（14）等号两边同时乘上Δt，并将t和t+1时间项整理到等式两边：

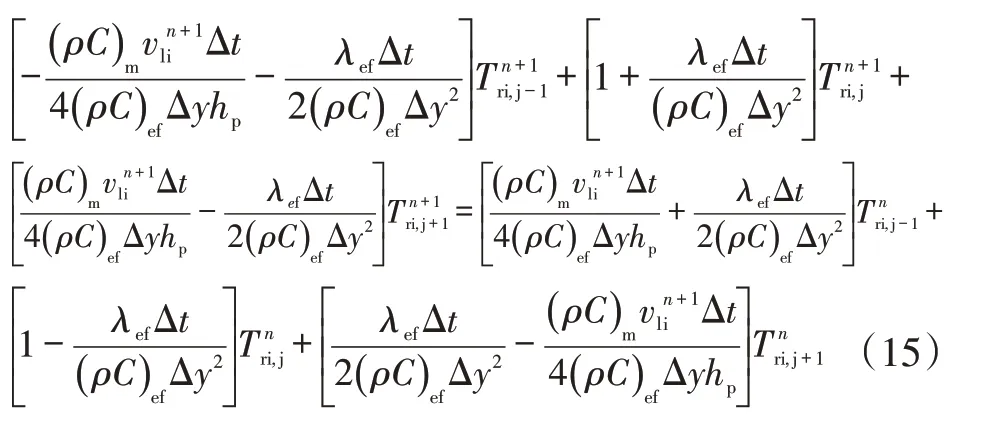
在已知近缝带地层内边界（裂缝壁面）温度时，采用追赶法可对上式进行求解。

2 实例分析

利用已建立的化学压裂裂缝温度场模型，结合算例进行模拟计算。模拟所用主要数据见表1。

相变压裂液和非相变压裂液在不同温度下具有不同的黏度，测定不同温度下二者的黏度值，拟合得到黏温关系函数见表1。

2.1 温度对裂缝几何尺寸的影响

分别计算裂缝温度恒定为地层温度、平均温度（注入温度与地层温度算数平均值）以及考虑温度沿缝长方向非稳态变化条件下的缝内温度场分布和裂缝几何尺寸，裂缝内温度分布见图3，裂缝高度、裂缝宽度见图4。

图3 不同计算条件下裂缝温度分布Fig.3 Fracture temperature distribution under different calculation conditions

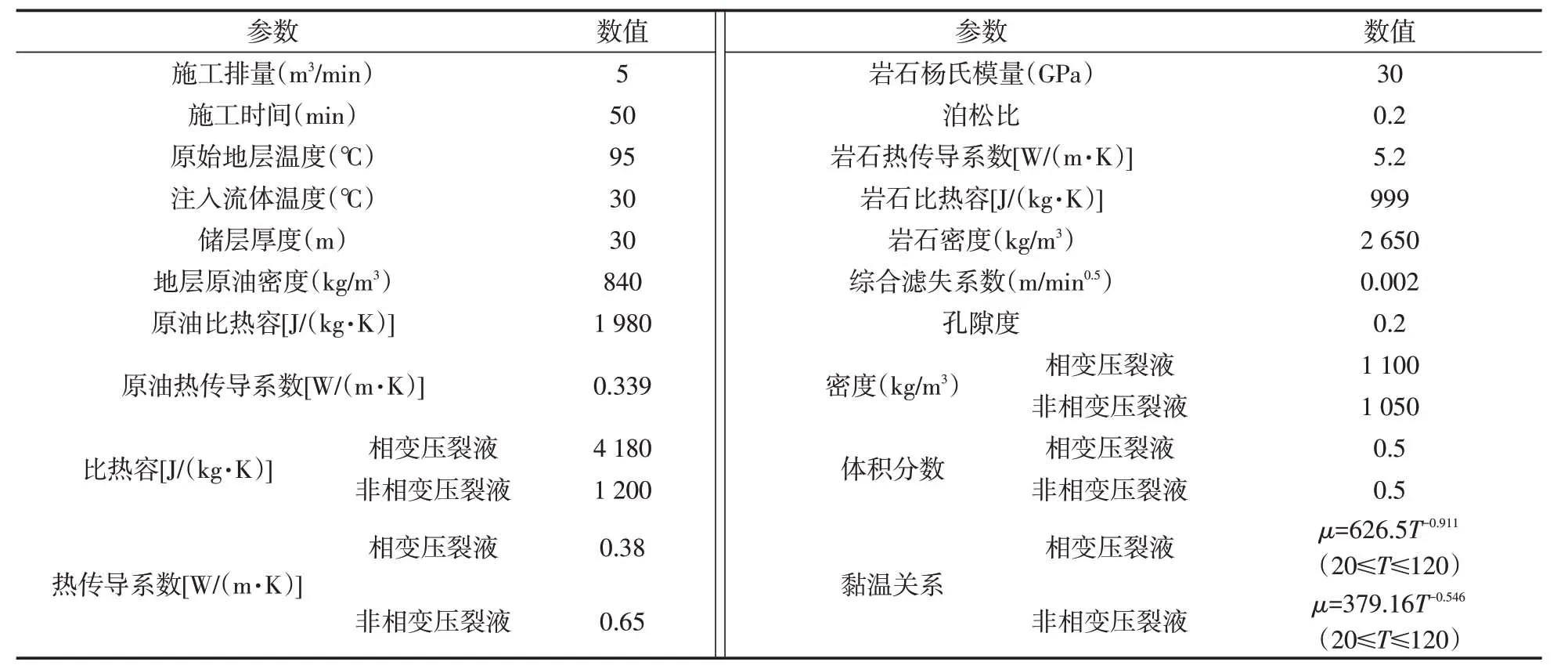
表1 模拟基础参数Table1 Simulated basic parameters

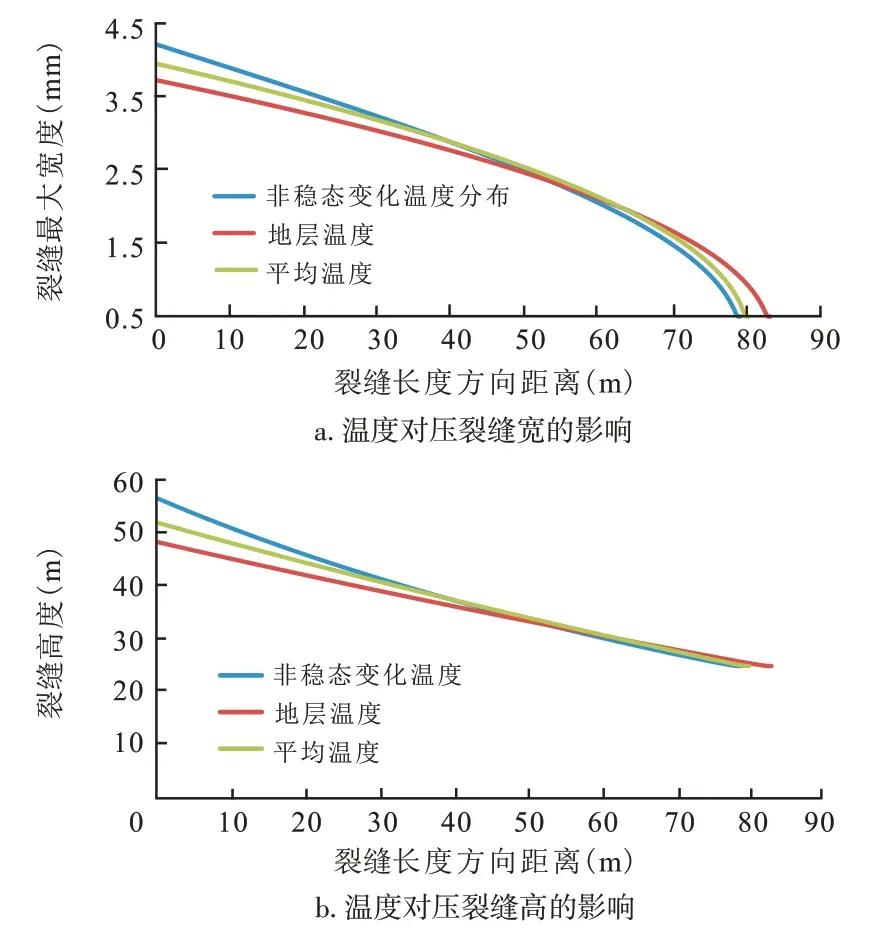
图4 温度对裂缝几何尺寸的影响Fig.4 Effect of temperature on fracture size

图3 表明，在化学压裂过程中，沿裂缝长度方向温度逐渐升高，裂缝前缘温度接近地层原始温度，裂缝入口温度接近注入流体温度，因此，可以按照不同的温度情况，把裂缝分为若干区域，针对每一区域，可选用不同相变温度的压裂液体系，达到“快速相变、有效支撑”的目的。

考虑缝内温度在缝长方向上非稳态变化时，相变压裂液和非相变压裂液组成的压裂液体系在缝长方向上具有不同的黏度值，导致计算得到的裂缝长度比地层温度、平均温度条件下计算的缝长小，在缝口处裂缝高度、裂缝宽度较大，在裂缝前缘，裂缝高度、裂缝宽度较小。不同条件下计算得到的缝长、最大缝高、最大缝宽见表2。

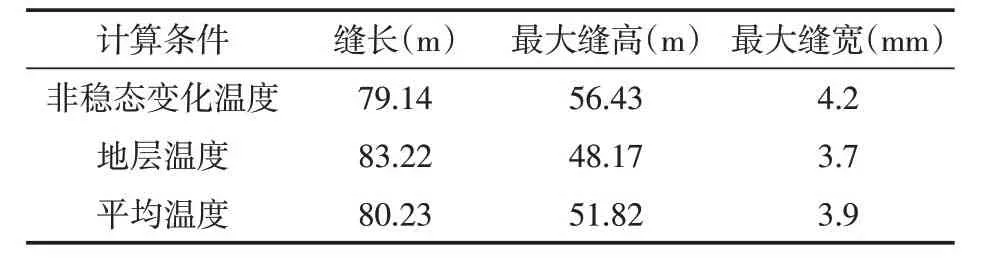
表2 不同条件下裂缝几何尺寸Table2 Fracture size under different conditions

从不同计算条件下裂缝几何尺寸来看，温度对压裂液体系黏度影响较大，进而影响裂缝几何尺寸，考虑温度变化对压裂液体系黏度的影响，能够更加真实、准确地反映水力裂缝拟三维延伸过程。

2.2 排量对温度场的影响

图5、图6为定液量250 m3，不同施工排量下（q=2，4，6，8 m3/min）缝内压裂液的温度、缝高、缝宽分布曲线。

在大排量下，容易形成更长、更宽的水力裂缝，裂缝入口端温度受排量影响较小，在前40 m 范围内温度变化不大，分布在30～50℃，超过40 m后，受水力裂缝尺寸，以及边界条件的影响，小排量下的水力裂缝内温度迅速升高，而大排量下的缝内温度上升幅度较小。

图5 排量对缝内温度的影响Fig.5 Effect of displacement on fracture temperature

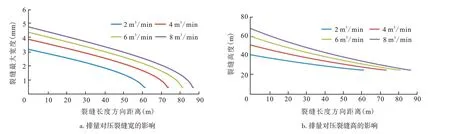
图6 排量对裂缝几何尺寸的影响Fig.6 Effect of displacement on fracture size

2.3 体积比对温度场的影响

由于两相液体热物性参数具有较大差异，因而其用量比也是影响缝内温度场的主要因素之一。图7为定排量5 m3/min，液量250 m3下，不同体积比（相变压裂液体积∶非相变压裂液体积=1∶0.5、1∶1、1∶2）条件下缝内温度分布曲线，图8为不同体积比条件下裂缝几何尺寸。

图7 体积比对缝内压裂液温度的影响Fig.7 Effect of volume ratio on temperature

图8 体积比对裂缝几何尺寸的影响Fig.8 Effect of volume ratio on fracture size

体积比对裂缝几何尺寸影响较小，但对缝内温度影响较大。比热容较大、热传导系数较小的相变压裂液体积越小，将同样体积的相变压裂液体积加热到某一温度所需热量就越少，裂缝前缘温度呈现缓慢上升趋势，缝内温度曲线平缓变化，缝内温度整体较高，反之裂缝前缘温度上升越快，裂缝前缘温度曲线越陡峭。

3 结论与建议

1）在拟三维裂缝模型的基础上建立了缝内温度场模型，并进行耦合求解。结果表明，裂缝几何尺寸、缝内温度场分布相互影响，在模拟计算缝内温度场、裂缝几何尺寸时，必须同时考虑二者相互关系。

2）施工排量、体积比对缝内温度分布具有显著影响。受水力裂缝尺寸、边界条件的影响，小排量下水力裂缝前缘温度迅速升高，而大排量下的裂缝前缘温度上升速度较慢；相变压裂液体积越小，裂缝前缘温度缓慢上升，缝内温度平缓变化，温度整体较高，反之裂缝前缘温度上升越快，裂缝前缘温度曲线越陡峭。

3）在化学压裂过程中，沿裂缝长度方向温度逐渐升高，裂缝前缘温度接近地层原始温度，裂缝入口温度接近注入流体温度，按照不同的温度区间，把裂缝分为若干段，针对每一段，可选用不同相变温度的压裂液体系，以达到提高支撑效果的目的。