一种改进的IGBT模块结温提取算法及实验研究

郭远欣，王学梅，张 波

（华南理工大学电力学院，广州 510640）

大容量的IGBT模块是电力电子变换器的主要器件，被广泛应用于高压直流输电、新能源系统、汽车牵引、高速列车、航天航空及军事等领域，其可靠性也受到越来越多的关注[1-3]。根据有关资料显示，功率器件是电流变换系统中失效率最高的部件，占比约34%[4]，而诱发电力电子系统失效的事故温度问题占比55%[5]。此外，功率器件的结温也是进行损耗计算、寿命预测和可靠性评估的重要参考。因此，对功率器件结温提取方法的研究十分有必要。目前针对功率器件的结温提取方法主要有：物理测温，如热电偶测温和红外测温；热阻抗模型预测法[6]；静态热敏感电参数法，如小电流饱和压降法和大电流注入法等[5]；动态热敏感电参数法，如阈值电压法、内部温敏驱动电阻法和内部寄生电感法等[7-10]。

结温的在线监测是为了实时获取器件的结温工况，进而研究器件的寿命和可靠性。功率器件结温在线监测的理想要求是，既不能打断被测装置的运行状态，也不能对被测装置造成干扰，同时还要保证足够的精度。动态热敏电参数法提取结温是比较适合的方法，目前用到的动态电参数主要有阈值电压[11]、开通延迟时间[12]、米勒平台电压[13]、关断延迟时间[14]、关断电压变化率du/dt[15]和电流变化率di/dt等[16-17]。文献[11,13]从线性程度、敏感程度以及实施难度方面比较了方法的优劣，其中缺点有：阈值电压和开通延迟对温度的敏感度较低，准确性不够高；关断和关断延迟时间需要高精度的传感器或提取电路，且鲁棒性不强；关断电压变化率的提取采用了并联电容，影响了电路的开关特性；开通电流变化率受到二极管反向恢复电流的影响，反映的不全是IGBT芯片的结温；最大关断电流变化率的传统提取方法用到电流互感器[16]，增加了装置的复杂程度，不易于集成，限制了其在工程方面的应用。

研究表明，在IGBT关断瞬间，di/dt与结温呈现较好的线性关系[17]，但由于关断过程非常短暂，di/dt的获取往往存在较大困难。Chen等[17]研究发现，可利用模块开尔文端子提取寄生电感两端电压，获得关断时的di/dt，从而间接获得器件结温。该方法优点在于，能在不破坏模块结构、增加较少辅助测量元件的情况下获取相关的温度敏感参数。但文献[17]仅给出了半导体物理表达式，证明了实验结果与理论分析趋势一致，而准确地提取这些半导体物理参数是困难的。另外，由于温敏参数和结温存在的非线性关系，目前曲线校准大多采用采集大量数据进行线性拟合的方法，繁琐且不能保证准确性，大大限制了该方法的推广应用。本文在文献[17]的基础上，提出了一种基于数值外推法的简化温敏参数模型和算法。通过该简化模型，可在不提取寄生电感参数和半导体参数的情况下，利用少量的数据获得温度特性曲线，进而快速提取IGBT的结温。

本文从半导体物理原理出发，分析推导了结温与相关电参数的简化算法模型，给出了最优基准点的选法，最后设计实验，验证了其正确性和实用性。

1 IGBT模块等效电路模型

以赛米控的IGBT模块SKM50GB12T4（1 200 V/50 A）为例，其外观及内部等效电路如图1所示，图1（b）中：粗线标示的为杂散电感存在的回路，据此得到考虑杂散电感的等效电路如图1（c）所示，其中，半桥的下管为待测元件，7脚和2脚间为杂散电感 LeE。

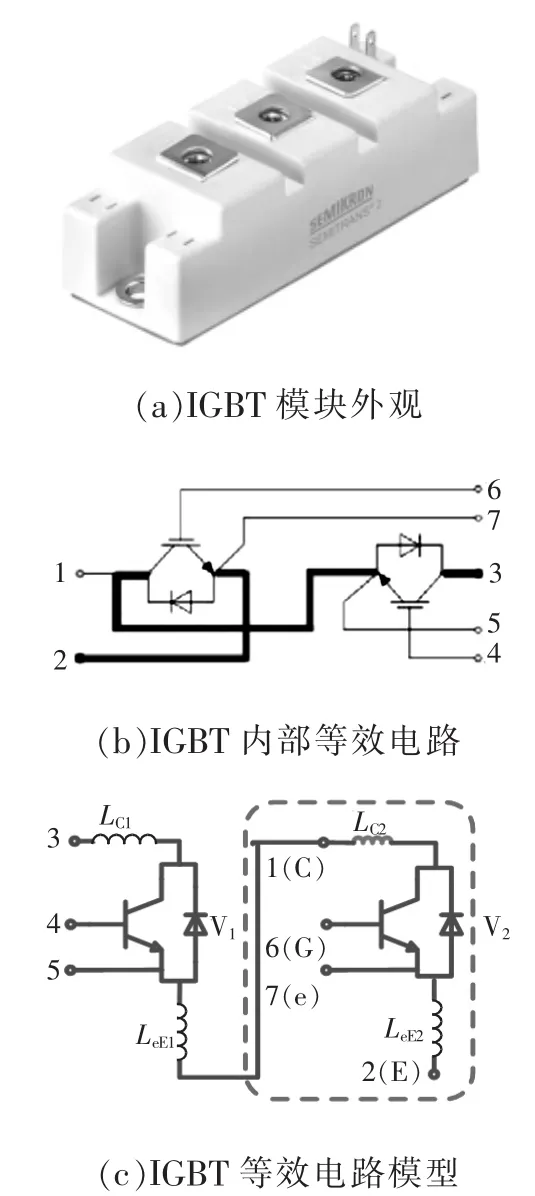
图1 IGBT模块外观及内部等效电路Fig.1 Appearance of IGBT module and its internal equivalent circuit

从等效电路模型可以得到开关管关断时杂散电感上的感应电压，即

通过测量电感电压veE可以间接得到关断时的电流变化率di/dt。杂散电感由于与温度无关，可看作常数，故讨论的主要是di/dt与温度的关系。

2 温敏电参数的解析分析

2.1 原理分析

场截止型IGBT增加了一个很薄的截止层，可以通过寿命控制技术有效减少截止层复合寿命，大大加快关断速度，其结构如图2所示[18-19]。

大部分IGBT的应用场合是用来控制输送到感性负载的功率。用于感性负载的IGBT关断波形可简化为图3。

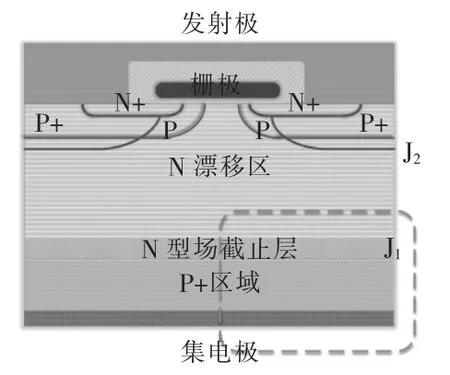
图2 场截止型IGBT结构Fig.2 Structure of field-stop IGBT

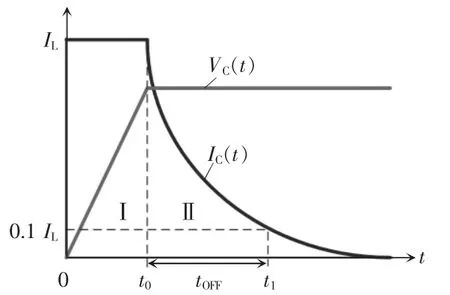
图3 IGBT的理想关断波形Fig.3 Ideal turn-off waveform of IGBT

关断过程可以大致分为2个阶段，阶段Ⅰ主要是电压线性上升阶段，阶段Ⅱ主要是集电极电流下降阶段。电流变化率di/dt发生在阶段Ⅱ，从半导体物理原理入手，分析阶段Ⅱ中电流变化率和温度之间的关系。

在电压上升之后，集电极电流的减小由过剩空穴和电子的复合决定。通常情况下，空间电荷层延伸通过大部分N型基区轻掺杂部分的宽度，所以集电极电流的减小由N型截止层中的过剩空穴复合决定。当不存在扩散时，N型截止层中空穴的连续性方程[18]为

式中：δpNF为N型截止层中的过剩空穴浓度；τHL,NF为截止层中的大注入寿命，即过剩载流子浓度衰减为起始浓度的1/e所经历的时间。由于N型截止层的掺杂浓度为1015～1016cm－3，注入的载流子浓度与其相当，故应采用大注入假设[19]。在N型截止层中都处于大注入状态，则方程的解为

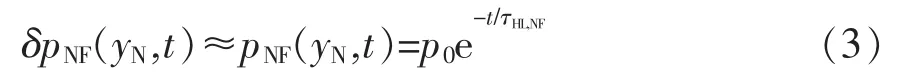
式中：pNF为J1处N型截止层中的空穴浓度；yN为耗尽区宽度；p0为P+集电极和N型基区之间结处的空穴浓度。

由于通态时载流子的注入，假定在阶段Ⅱ开始时，存储电荷区内的空穴浓度等于p0。截取图2中J1结部分，两边的载流子分布情况如图4所示，进而可以分析支撑存储电荷区内载流子复合的集电极电流。

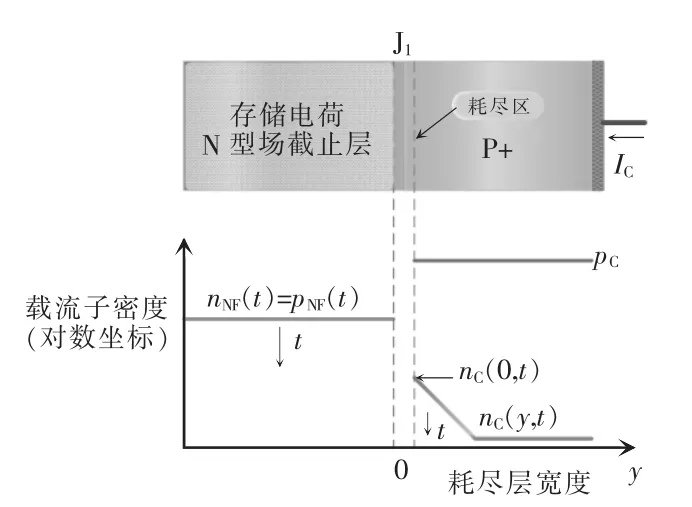
图4 场截止型IGBT关断时J1结两边的自由载流子分布Fig.4 Distribution of free carriers on both sides of junction J1 when field-stop IGBT is turned off

为了简化分析，可以假定在PN结J1附近的N型截止层中的载流子浓度与距离无关，只是如式（3）给出的时间的函数。N型截止层中过剩空穴的存在引起电子注入P+集电极区域，这些电子朝y方向扩散，引起浓度指数式衰减，如图4所示。根据PN结定律，J1两边的自由载流子浓度关系为

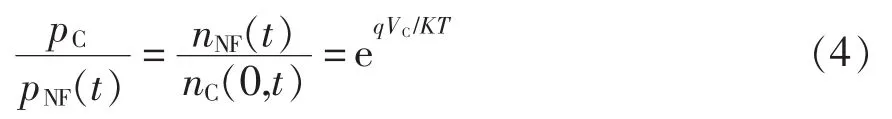
式中：nNF为N型截止层中的电子浓度；pC为P+集电极区域的空穴浓度；nC（0，t）为 P+集电极区域的电子浓度；q为电子电荷量；VC为PN结J1的势垒电压；K为玻尔兹曼常数；T为温度。

由于处于大注入状态，扩散进入P+集电极区域的电子呈指数分布，则有

式中，lnE为P+集电极区域内电子的扩散长度。

这些注入P+集电极区域的电子扩散形成了集电极电流，结合式（5）则有

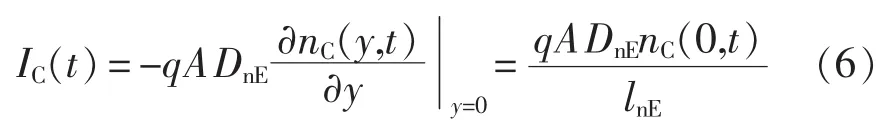
式中：A为芯片面积；DnE为P+集电极区域的电子扩散常数。

根据式（3）、式（4）和式（6）得到

对于感性负载，在阶段Ⅱ中开始下降时集电极电流等于负载电流IL，故上述方程可写为

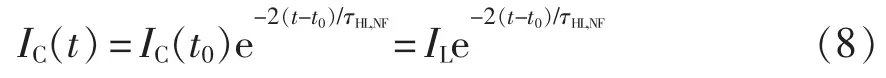
即集电极电流随着时间以指数形式减小，其时间常数等于N型截止层中的大注入寿命的一半。

集电极电流关断时间tOFF定义为电流减小到其导通的1/10时所用的时间，如图3所示，结合式（8）可以得到

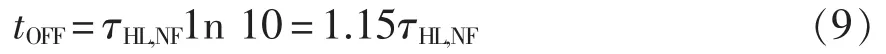
对式（8）求导可以得到关断电流变化率

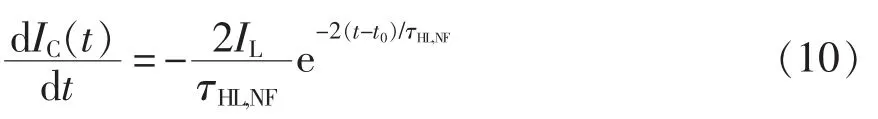
最大关断电流变化率在t0时刻取得，即

将式（11）代入式（1），即可得到所要求的温敏（电）参数的表达式，即

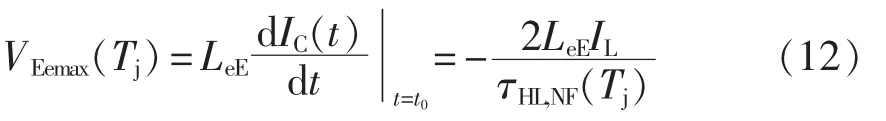
可以看出温敏参数仅由寄生电感、负载电流以及N型截止层的大注入寿命τHL,NF决定。假设通态电流与温度无关，温度只通过影响N型截止层的大注入寿命来影响温敏参数，随着结温升高，大注入寿命τHL,NF增加，温敏参数VEemax的绝对值减小。

2.2 基于外推法的温度特性的简化模型

大注入寿命τHL,NF的温度经验公式[20]为

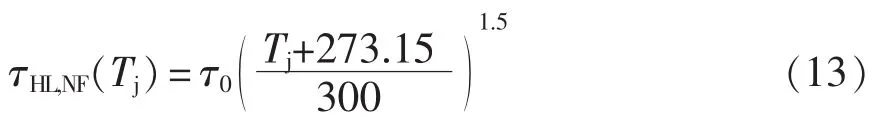
式中，τ0为26.85℃时的大注入寿命。代入式（12），得到动态温敏参数VEemax和温度的关系为

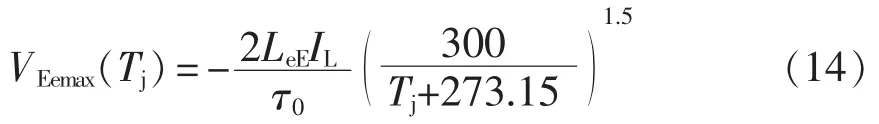
由式（14）可知，VEemax与负载电流 IL、寄生电感LeE、大注入寿命τ0和结温Tj相关。由于准确提取寄生电感LeE和大注入寿命τ0比较复杂和困难，且不同老化程度的器件这2个参数也会有所不同，因此有必要避开这2个物理量，提出更简便实用的方法。对式（14）进行变换，得到结温测量的表达式为

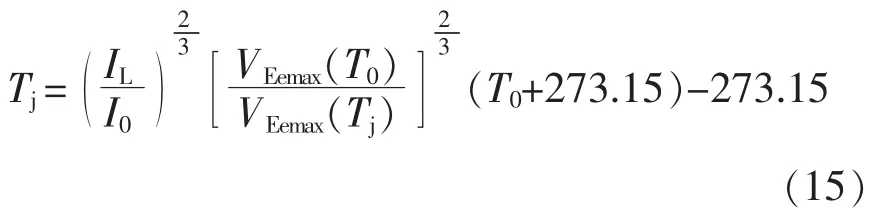
式（15）仅需测量一组初始数据（I0，T0，VEemax（T0）），即可外推出其他电流IL和温敏参数VEemax（Tj）下的结温，同时避开了寄生电感和大注入寿命的提取。

在20～140℃之间对式（13）进行线性化近似，拟合结果如图5所示，去除式（15）中的分数指数项，进一步变换得到一个非常简洁的测温表达式，即

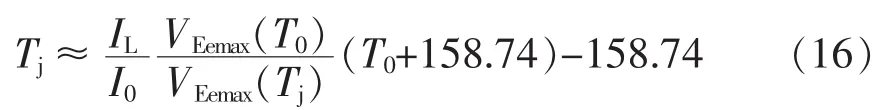
可以推断出基准值点（I0，T0，VEemax（T0））的选取直接决定了外推结果的好坏。

图5 归一化大注入寿命的线性拟合Fig.5 Linear fitting of normalized large injection lifetime

3 实验验证及结果分析

3.1 实验电路设计

小电流饱和压降法是静态温敏电参数法中准确度和线性度较高的方法[21]，但其必须要打断电路原本的运行状态，不适用于结温的在线监测。为了能在不破坏模块封装的前提下利用这种方法测量IGBT的瞬时结温，本文对双脉冲实验加以改进，设计了一个将双脉冲实验与小电流饱和压降法相结合的实验电路，如图6所示，能同时获得温敏电参数VEemax和与之对应的IGBT瞬时结温。改进双脉冲实验电路的设计主要是增加一个开关管V1，控制电路在双脉冲测试和小电流饱和压降测量间切换，实验时序如图7所示。

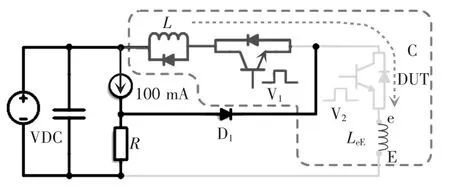
图6 改进双脉冲实验电路Fig.6 Circuit of improved double-pulse experiment

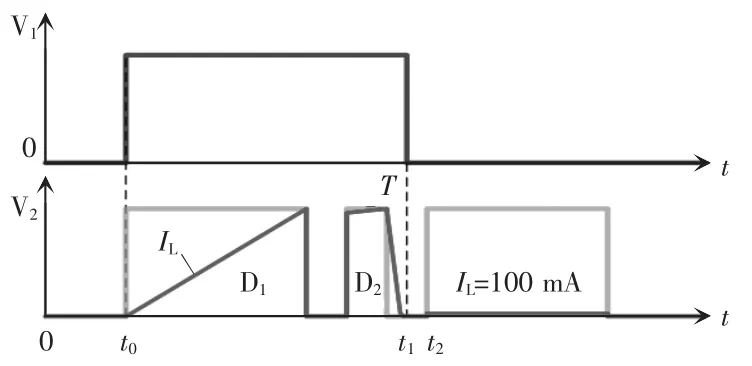
图7 改进双脉冲实验时序Fig.7 Timing sequence of improved double-pulse experiment

实验基本原理如下。图6开关管V2为待测元件,虚线箭头所示支路与普通双脉冲电路基本无异，不再赘述，不同之处在于用开关管V1来控制切换流经待测元件的电流。电阻R一方面用来给100 mA电流源续流，另一方面起到自动切换电流支路的作用。二极管D1起到限制电流方向和防止过流的保护作用。t0时刻V1和V2同时脉冲触发，到t1时刻以前与普通的双脉冲实验无异，用以测量开关波形；t1时刻V1管脉冲信号关断；在t2时刻（几μs之后）V2脉冲再次触发，待测元件流过电流切换为100 mA的恒流源，此时测量V2的饱和压降用以计算结温。实验装置包括恒流源电路、续流二极管、空心电感、母线电容、恒温加热台中央、DSP和驱动电路，如图8所示。

图8 实验装置Fig.8 Experimental setup

3.2 结温测量校准

为了用小电流饱和压降法获取结温，需要对其结温曲线进行校准。方法如下：将待测IGBT模块底部均匀涂上导热硅脂，安装在高精度恒温加热台上（控温精度：±（1～2）% ℃），设定加热台初始温度并对待测元件加热足够长时间，待温度稳定20 min后进行实验，此时可认为结温等于壳温，即设定的初始温度。V1管保持关断，测量100 mA时的IGBT饱和压降VCEsat，实验数据见表1。根据实验数据绘制曲线如图9所示。

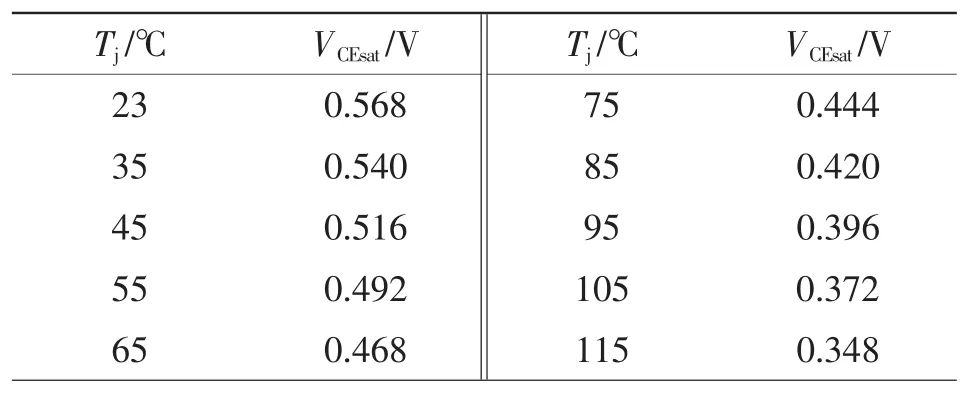
表1 IGBT结温Tj和饱和压降VCEsat实验数据Tab.1 Experimental data of IGBT junctiontemperature Tj and saturation voltage drop VCEsat

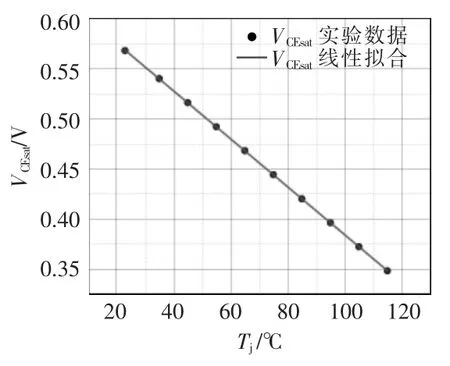
图9 IGBT Tj-VCEsat实验曲线及拟合结果Fig.9 Experimental curve and fitting result of Tj-VCEsat

拟合的线性相关程度很高，残差平方和为4.097 89×10－7，相关系数 r=0.999 9。拟合得到的关系式为

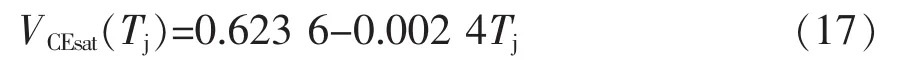
可以看出温度灵敏度为2.4 mV/℃。根据式（17），通过测量饱和压降VCEsat倒推得到的结温Tj作为对应温敏电参数VEemax自变量。

3.3 实验及结果分析

用高精度恒温加热台加热待测器件至设定温度稳定20 min后，进行不同电流、不同温度下的改进双脉冲实验。测得负载电流为20 A、温度为50℃时IGBT关断过程中的实验波形如图10所示，对应的饱和压降波形如图11所示。为了提高准确程度，将采集的VCEsat数据做统计处理，取置信度95%内的均值。将得到的饱和压降值代入式（17）计算得到实时结温，对应结果见表2，其中Tc为模块壳温，即加热台设置的温度。结果表明电流越大，结温与加热台设置的温度差别越大，原因是器件的自热。

为表示方便，记VEemax=－|VeE|max。对应上述设置温度的VEemax实验数据如表3所示。

根据表2和表3绘制实验曲线如图12所示。

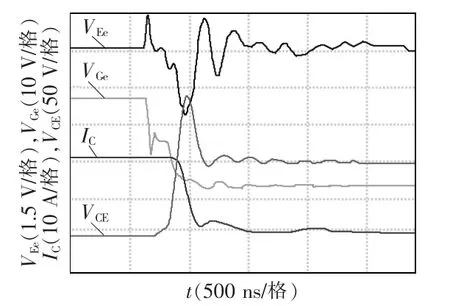
图10 IL=20A、50℃下IGBT关断时的VeE波形Fig.10 Waveforms of VeE during IGBT turn-off under IL=20 A and 50℃

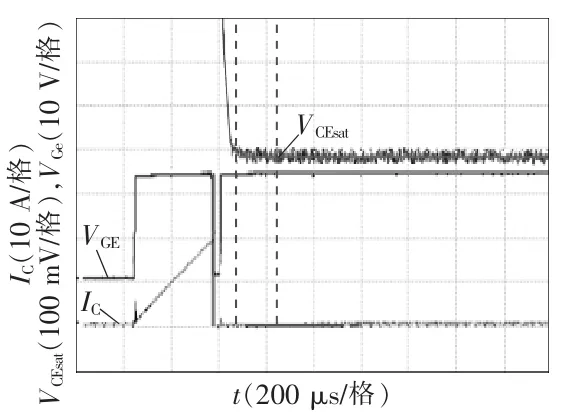
图11 IL=20 A、50℃下IGBT关断过程中的饱和压降波形Fig.11 Waveform of saturation voltage drop during IGBT turn-off under IL=20 A and 50℃

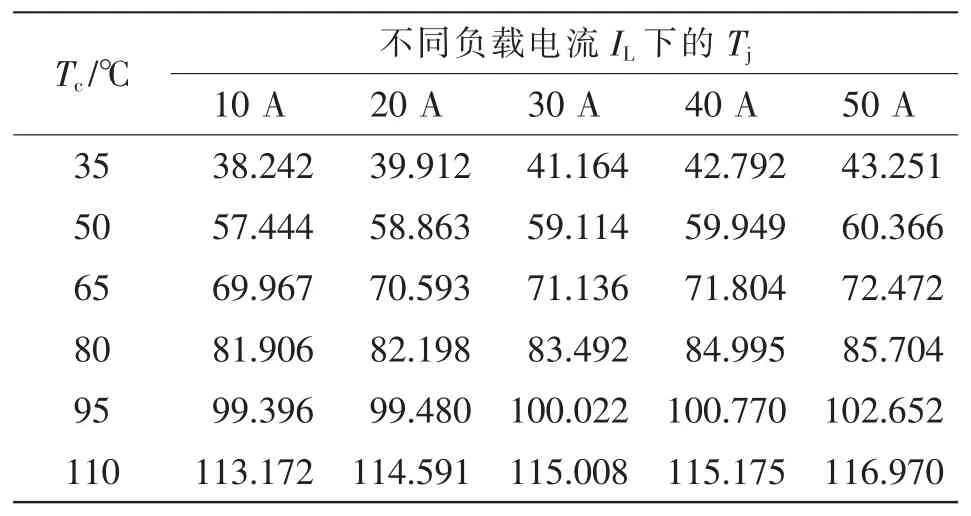
表2 饱和压降法得到的结温TjTab.2 Junction-temperature Tj obtained using the saturation voltage drop method℃

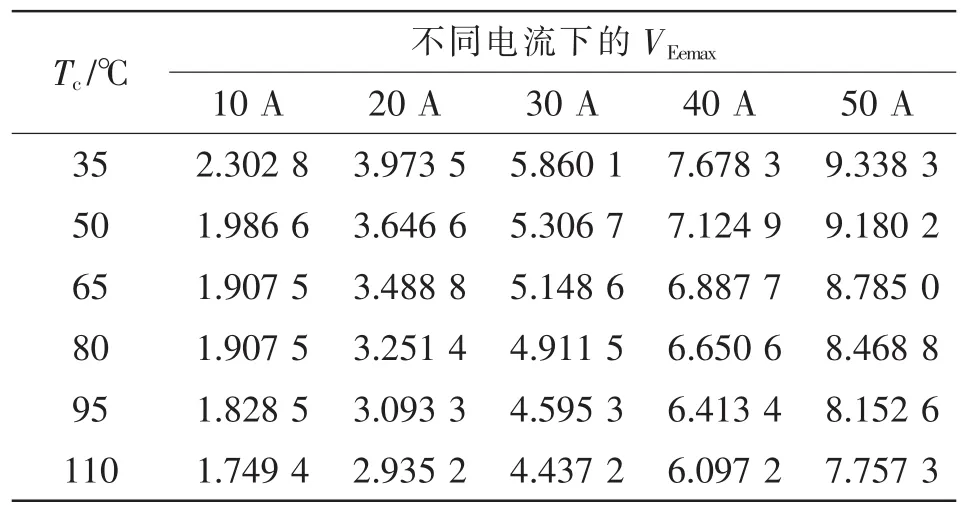
表3 IGBT关断时不同温度和电流下的VEemax实验数据Tab.3 Experimental data of VEemax during IGBT turnoff at different temperatures and currents V

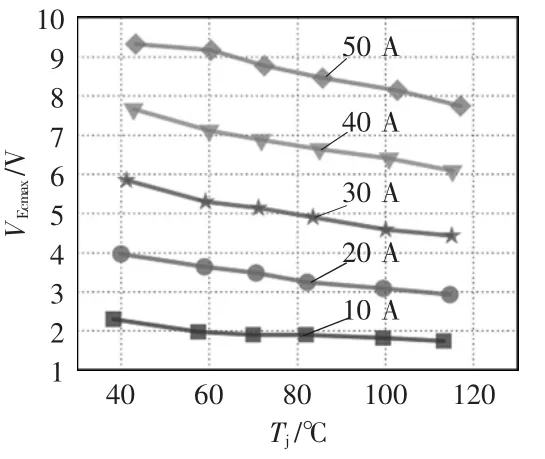
图12 不同电流、峰值电压VEemax的实验温度曲线Fig.12 Experimental curves of temperature vs peak voltage VEemax at different currents

首先验证前文所提式（14）的正确性。

为了获得杂散电感LeE，将式（1）两端对时间积分，即

根据式（9）和式（13）可以计算τ0的大小。模拟计算的参数参考值如表4所示。将参数代入式（14），得到电流10～50 A时的理论模拟温度曲线与实验结果的对比，如图13所示。

从图13可以看出，实验结果和理论模拟的结果基本吻合，温度越高，峰值电压VEemax越大，VEemax随电流近似等比例增加，验证了式（14）的正确性。

接着验证所提简化模型和算法的正确性。前面提到过基准值点（I0，T0，VeEmax（T0））的选取直接决定了外推结果的好坏，因此有必要推导一个基准点选取优劣的判据。

根据式（14），定义参数 Rmax（Tj）为 dIC/dt在电感LeE上产生最大感应电压的等效温敏电阻，其量纲为Ω，则有

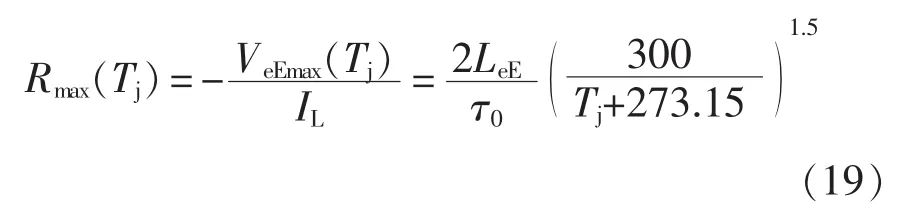
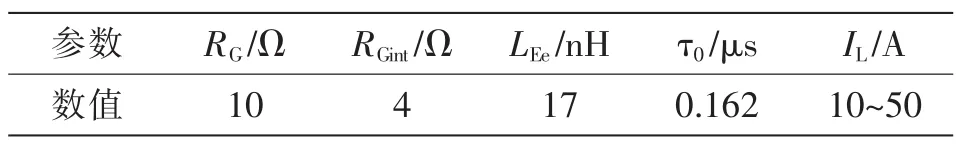
表4 参数参考值Tab.4 Reference values of parameters

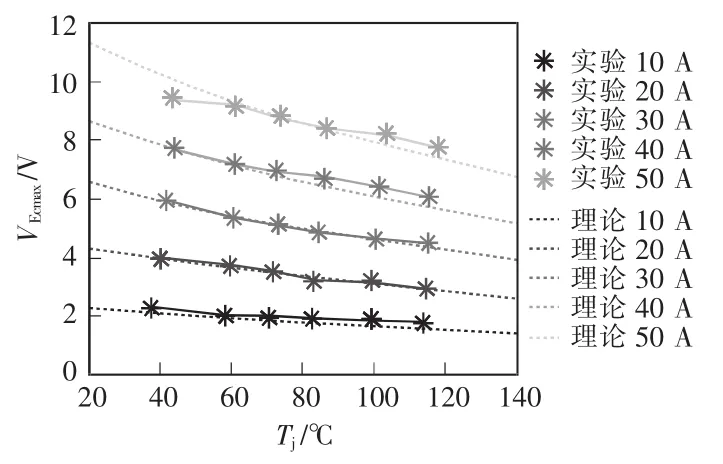
图13 实验和理论结果比较Fig.13 Comparison between experimental and theoretical results

由式（19）可知，同一温度下不同电流计算出的参数Rmax应该相等。因此，以不同电流下计算出的Rmax的标准差δRmax作为基准点选取优劣的判据，标准差越小，选取的点越好。为了给出衡量选取点好坏程度的量化标准，对式（19）作线性化处理，得

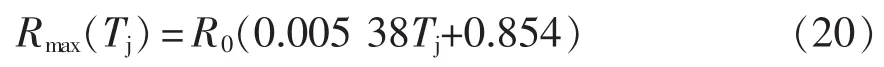
式中，R0=2LEe/τ0。进一步推导可以得到温度误差为ΔT时所对应的参数百分比误差ΔRmax（%），即

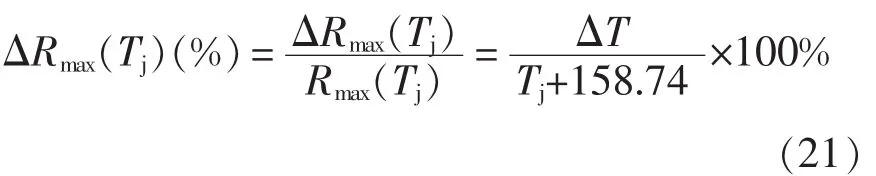
百分比标准差δRmax（%）的计算公式为

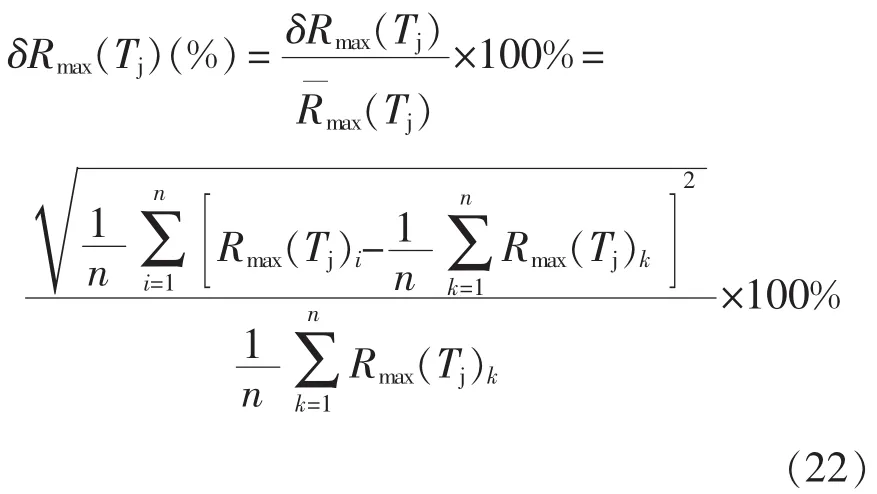
至此，判断基准点选取的好坏就有了具体的标准，即：如果计算出的标准差 δRmax（%）最小，那么该点就是误差最小的数据点，也就是最佳参考基准点，根据式（15）或式（16）模型所得到的结果就最优。更进一步地，该判据还可以用来剔除误差较大的数据点。

根据式（19）、式（21）和式（22），计算基准点选取的判据如表5所示。

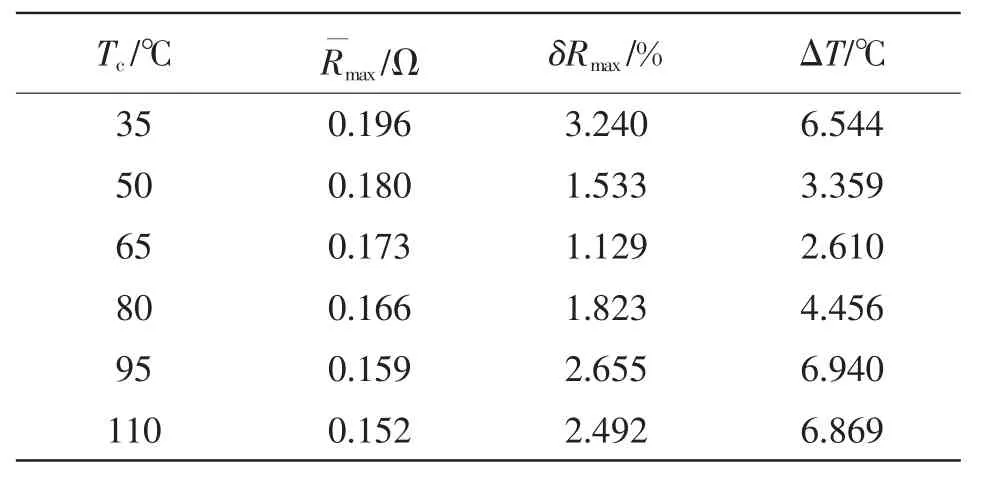
表5 基准点选取判据（IL=10～50 A）Tab.5 Selection criterions for reference points（IL=10～50 A）

由表中可以看出，Tc=65℃时的百分比标准差δRmax（%）1.129最小，由此计算得到温度误差不超过2.610℃，故此为所得数据中的最佳基准点。

以表2和表3中的第3行为参考基准值，用简化模型式（16）得到的外推计算结果与实验对比如图14所示。可以看到用简化公式外推计算的结果和实验的结果比较接近，初步验证了所提模型和算法的正确性。

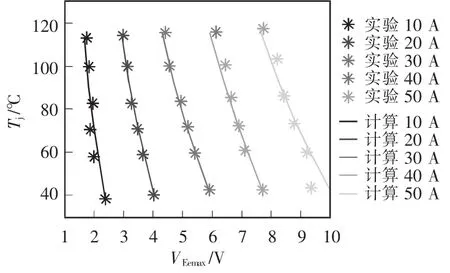
图14 外推计算和实验结果对比1Fig.14 Comparison between extrapolation calculations and experimental results （Case 1）

为验证算法和实验的实用性，在Ee两端并联一个nH小电感以减小寄生电感LeE，再次实验，结果如表6和表7所示。根据判据表7，选取误差最小的第2行作为参考基准值，温度误差不超过1.352℃。将数据代入式（16）可得到外推计算和实验的结果对比，如图15所示。

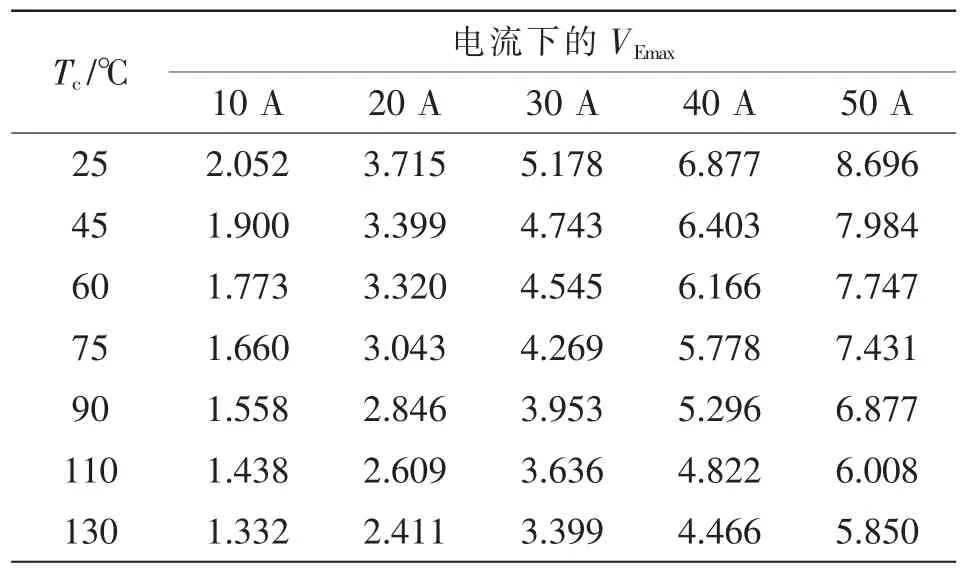
表6 改变电感后IGBT关断时不同温度和电流下的VEemax实验数据Tab.6 Experimental data of VEemax during IGBT turnoff at different temperatures and currents（after changing the inductance）V

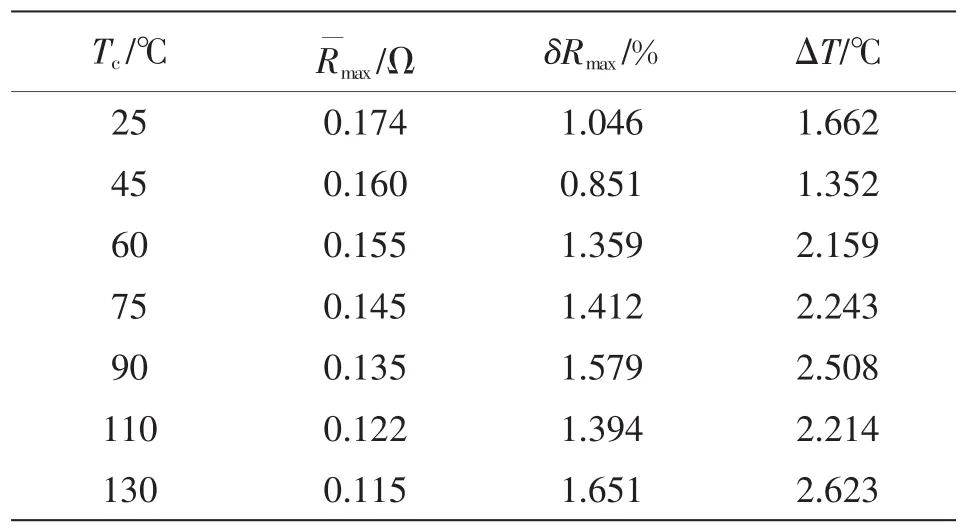
表7 改变电感后基准点选取判据（IL=10～50 A）Tab.7 Selection criterions for reference points after changing the inductance（IL=10～50 A）

此次计算结果和实验的重合度更好，主要原因是分布电感减小后，由电感引起的干扰减小，感应电压的幅值和扰动减小，对应的δRmax（%）更小，所选的基准点更好，因而计算结果和实验的吻合程度更高。对比结果再次验证了所提模型和算法的正确性和实用性。

通过上述过程可知，在实际使用时，式（16）将会带来极大方便，只需测量几组数据，并依照判据表选择合适的基准值，即可外推得到任意电流和温敏参数对应的温度，并且准确程度较高。该算法不仅可以大大简化实验的校准工作量，还可以减少寄生参数和大注入寿命测量不准确及其他不确定因素带来的干扰，适用于工程应用和推广。

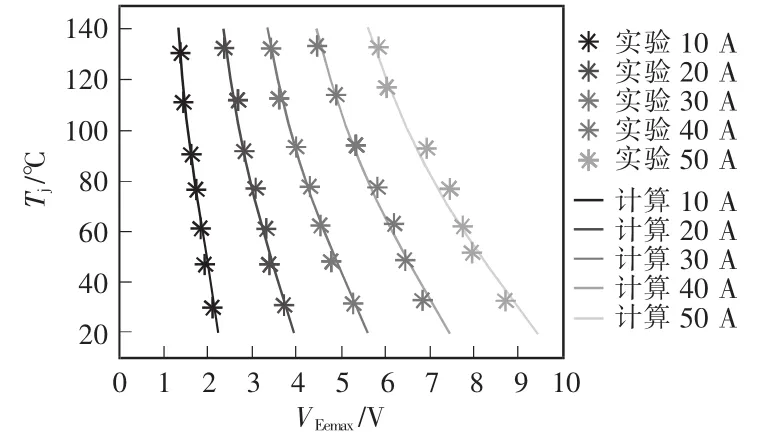
图15 外推计算和实验结果对比2Fig.15 Comparison between extrapolation calculations and experimental results （Case 2）

4 结语

器件的结温状况是进行电力电子器件可靠性分析的一个重要依据，利用温敏电参数在线提取结温是当下的热点。本文从IGBT模块的结构特点出发，依据半导体物理原理分析推导了IGBT关断时的杂散电感电压和结温的数学关系，并进一步简化得到不需要提取寄生电感和大注入寿命参数的结温测量模型。推导出了最优基准点判据公式，提出的基准点外推算法在大大降低温度曲线校准复杂度的同时保证了其准确度。设计利用小电流饱和压降法测量器件动态结温的改进双脉冲实验,对所提算法模型进行了验证，所提改进方法具有破坏性小、简便实用和集成性好的特点。该实验及算法尚未考虑器件老化对结温测量的影响，其影响程度有待进一步研究。