浅析基于FPGA的Mish函数实现

肖祥位 蔡敬菊 徐智勇

1. 中国科学院光电技术研究所国家光束控制重点实验室 四川 成都 610209；2. 中国科学院光电技术研究所 四川 成都 610209；3. 中国科学院大学 北京 100049

引言

随着计算机处理能力的提高，神经网络再次成为人工智能领域的研究热点。目前主流的方式仍然是基于CPU/GPU对算法进行实现，但由于神经网络算法具有庞大的计算量，使得在传统平台上实现存在实时性不强、功耗过高、体积较大等缺陷，极大地限制了神经网络算法的落地应用。因此目前该方向的理论研究和实际应用方面存在着较大的脱节。现场可编程门阵列(FPGA)可以通过硬件描述语言对电路进行描述，可以构建大型电路实现并行计算。使用FPGA实现AI算法，极大地加快了计算速度，提高实时性，降低系统功耗。为AI算法落地提供强有力的支撑。

Mish函数是YOLOv4及其衍生版本里面用得较多的一个激活函数，是整个网络中实现非线性运算的关键。Mish函数的使用使得整个网络检测效果得到了很大程度的提升，它的非单调平滑性相比于其他激活函数有着更好的表现。想使用FPGA对YOLOv4及其衍生网络加速则不可避免地要在FPGA上实现Mish函数。本文首先对Mish函数进行介绍，提出几种不同的实现方案，通过对不同方案的对比分析，最终确定以多折线拟合与查找表组合的方式进行实现。并通过对硬件的实现分析，确定其误差在较小的范围，为使用FPGA加速YOLOv4及其衍生网络奠定基础[1]。

1 Mish函数简介

卷积神经网络中激活函数是对线性卷积输出的结果进行非线性计算 以此来模拟神经网络中的神经元模型。Mish函数则是对卷积层的输出进行非线性激活，以此实现非线性计算。Mish函数的表达式如下：

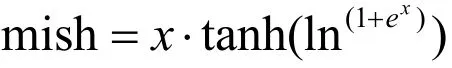
Mish函数是一个非单调函数，其函数图像如图1所示。可以看出Mish函数在输入值小于-10的时候函数值非常接近于0，我们在误差可以接受的范围内认为该函数值等于0。在输入值大于4.7的时候我们可以近似的认为该输出的值和输入的值是相同的。我们可以看出输入值从-10到4.7的过程中，输出是先减小然后逐渐增大的过程。如果是在FPGA上直接实现Mish函数，则会涉及指数运算、反正切运算以及对数运算。我们都知道这些计算在硬件上实现是非常困难的而且还会消耗大量的计算资源。这在硬件上实现整个YOLOv4算法时完整的实现Mish函数是不可能的。因此我们需要考虑一种简单、高效的方式来近似Mish的非线性功能。本文通过分析最终采用多折线拟合的形式在硬件上实现Mish函数[2]。

图1 Mish函数图像

2 方案选择

FPGA实现复杂函数常用的方法有：泰勒展开法、查表法、多项式拟合法、分段拟合法、CORDIC算法等。泰勒展开法对于复杂函数时，要保证精度的前提下往往需要展开成多阶函数才可以进行拟合，但是在FPGA中展开阶数越高实现起来所需要花费的乘法器资源也就越多，在神经网络中Mish函数的使用往往是并行执行多个相同的乘法，所以在片上DSP资源有限的情况下，我们希望尽可能少的使用DSP,因此使用泰勒展开在实现Mish函数来说耗费乘法器资源过多。基于查表法的FPGA实现是实现复杂算法最方便最快捷的方式，同时查表法还可以达到较高的工作频率，但是在实现精度要求较高的场合需要较大位宽才能表示，所以需要耗费较大的逻辑资源。基于多项式拟合的方式实现复杂算法，是将算法分成若干段，然后用多项式分别进行拟合，拟合的效果较好可以达到较高的精度，但是仍然存在使用乘法器资源较多的不足。基于CORDIC算法的实现所消耗的资源较少但是耗时较多而且精度不高。基于分段拟合的方式，采用最小二乘法进行拟合，可以将函数分成较多的小区间，在每个区间分别进行拟合，这样可以保证精度的同时保证使用乘法器资源较少[5]。

本文则是使用分段拟合的方式将函数区间分成若干子区间进行分段拟合，由于保证拟合精度因此分段区间较多，在硬件实现上我们将查找表考虑进来，使用查找表的方式将每个拟合函数的系数存放在查找表中，实现较高频率的读取，然后在使用一个乘加器将数据进行计算输出，保证了较高精度的同时提高了频率，提升了整体的性能。

3 Mish函数设计

3.1 Matlab拟合

使用matlab对Mish函数进行分段拟合，每段采用最小二乘法进行拟合，使得拟合误差控制在0.001以下。在误差允许范围内当输入大于4.7时输出和输入相等，当输入在小于-10时我们可以接受输出等于零，因此只需拟合[-10,4.7]之间的函数值。本文将整个区间分为43个小区间，采用最小二乘法进行分段线性拟合[6]。各区间的拟合如下表所示：

表1 Matlab分段拟合Mish函数

图2表示的是输入区间在[-10,10]内，取点间隔为0.01。采用分段拟合的方式将真实值与拟合值做差取得拟合误差，可以看出本文设计的分段拟合方案与真实的Mish函数非常接近，误差控制在0.001以下，不会对结果产生误差[7]。

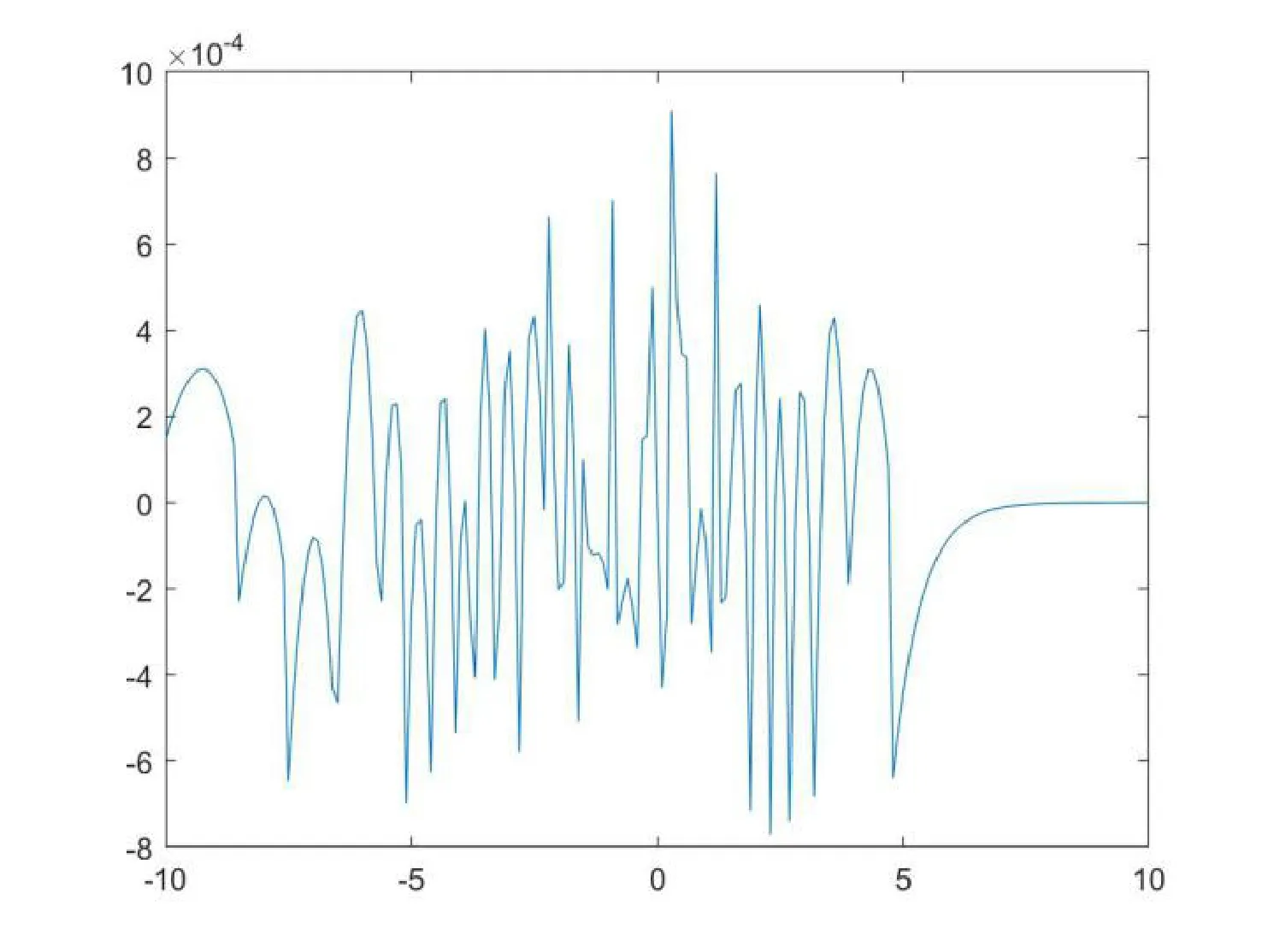
图2 Mish函数Matlab拟合误差曲线

在区间[-10,10]内随机取点15个，得到拟合误差最大在0.0006，低于0.001。符合我们上面的分析。具体拟合误差如下表2：

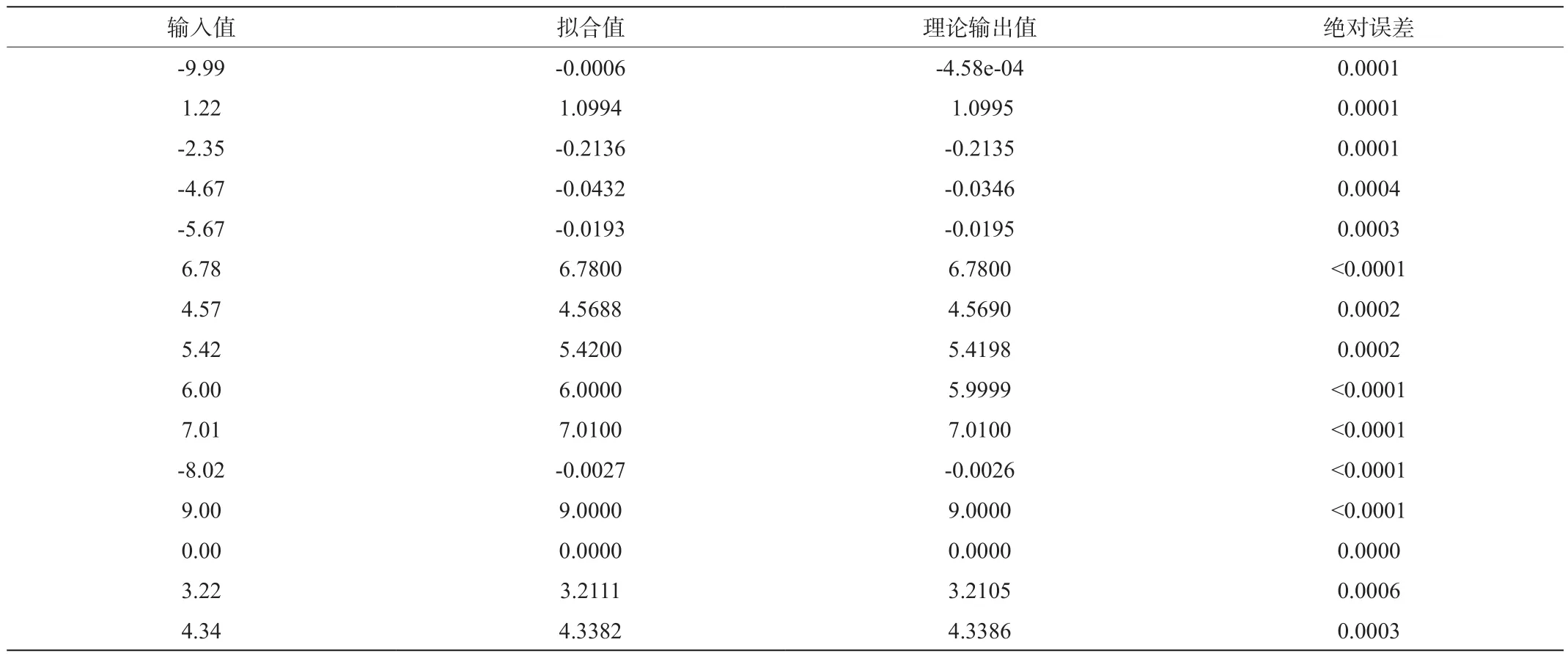
表2 Mish函数随机取点拟合结果

3.2 FPGA实现

本文采用AC620平台进行设计实现，一般而言在软件层面实现Mish函数往往采用32位浮点的形式，但是在FPGA中如果采用浮点计算则会消耗大量的浮点乘法器以及大量的逻辑资源，考虑资源使用率以及运算速度等因素我们将在FPGA上定点小数对Mish函数进行实现，有效的兼顾了资源使用、运行速度。同时我们仿真分析采用16位定点小数的形式实现Mish函数不会对网络最终分类结果产生误差。因此我们在FPGA上采用16位定点小数对Mish函数进行实现[8]。

本文采用有符号数的数据进行计算，因此输入输出数据第一位为符号位。输入数据进行量化的过程中将输入数据同时扩大2048倍，将所有的输入值进行量化取整以便作为FPGA的输入。同时也将拟合的所有折线进行扩大2048倍并将所有系数通过四舍五入的形式取整。将这些系数通过建表的方式预先存储在FPGA内部，当不同输入进来的时候，对应输出相应的系数参与计算。这样极大地保证了系统运行的速度与稳定性。量化以及误差修正处理后Mish函数在FPGA平台的拟合函数表达式如下表3：

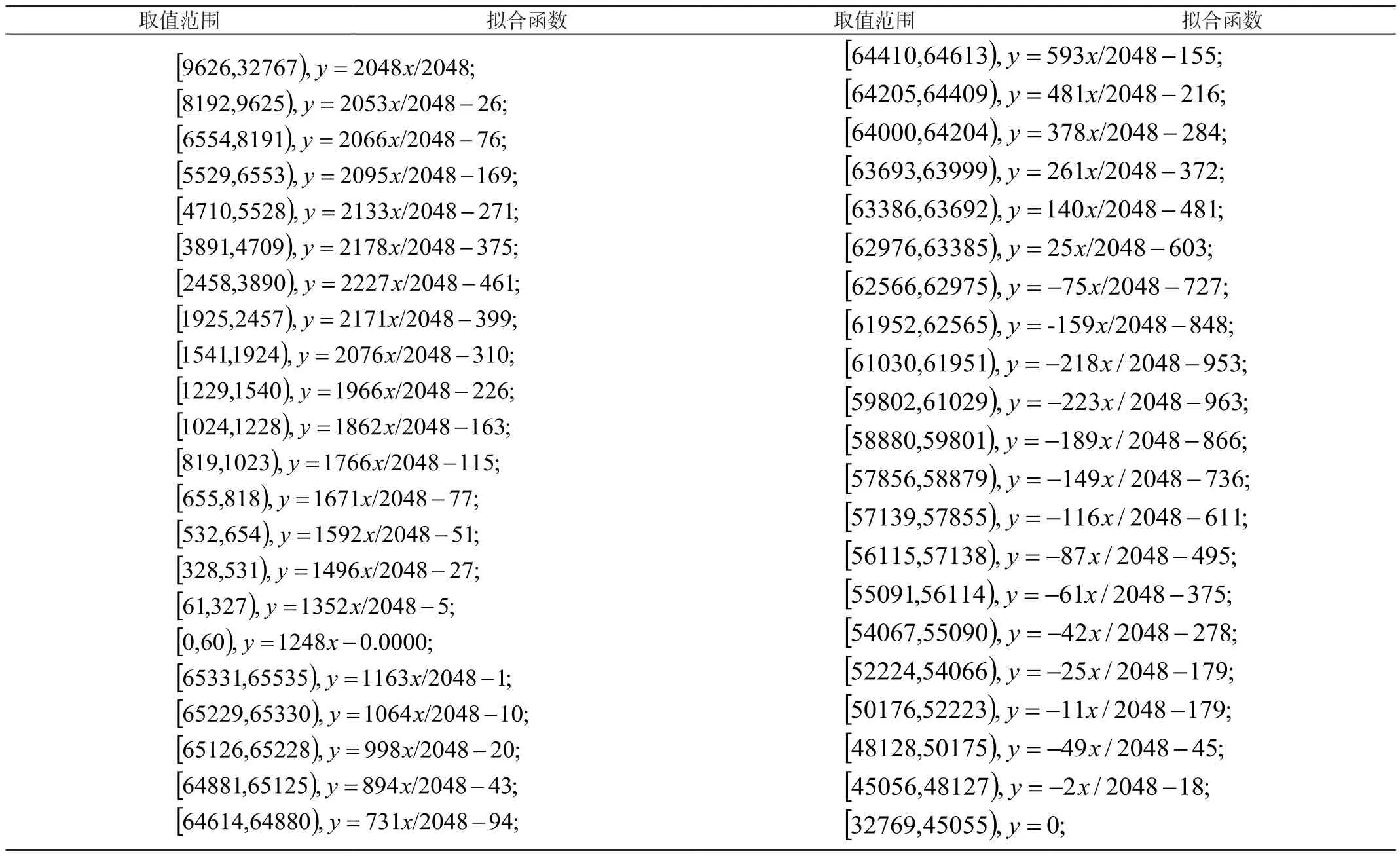
表3 FPGA拟合Mish函数

运算过程中使用的是有符号数，因此在输入值进行量化时，将负数的输入值以补码的形式进行表示。而在拟合折线的函数表达式中，对输入值扩大了2048倍，因此需要对其进行右移11位还原为原输入大小才不会对输出结果产生影响[3]。

图3 FPGA拟合Mish函数误差曲线

如图3所示，表示了在FPGA上实现Mish函数的误差，这跟图2相比有一定的差距，差距主要来源于量化过程中的四舍五入以及对输入数据的截位处理所产生的误差。但根据图3所示的误差中可以看出，用FPGA拟合后的Mish函数绝对误差仍然低于0.002。这对我们进行神经网络的分类精度不会带来太大的差别。这与表3随机抽取的15个数据表示结果一致，从表3我们可以看出只有少数点误差在0.0013左右，但是总体都低于0.002。综合分析对Mish函数采用上述拟合方案，总体误差较小均控制在0.002以下，对神经网络输出结果无影响[4]。

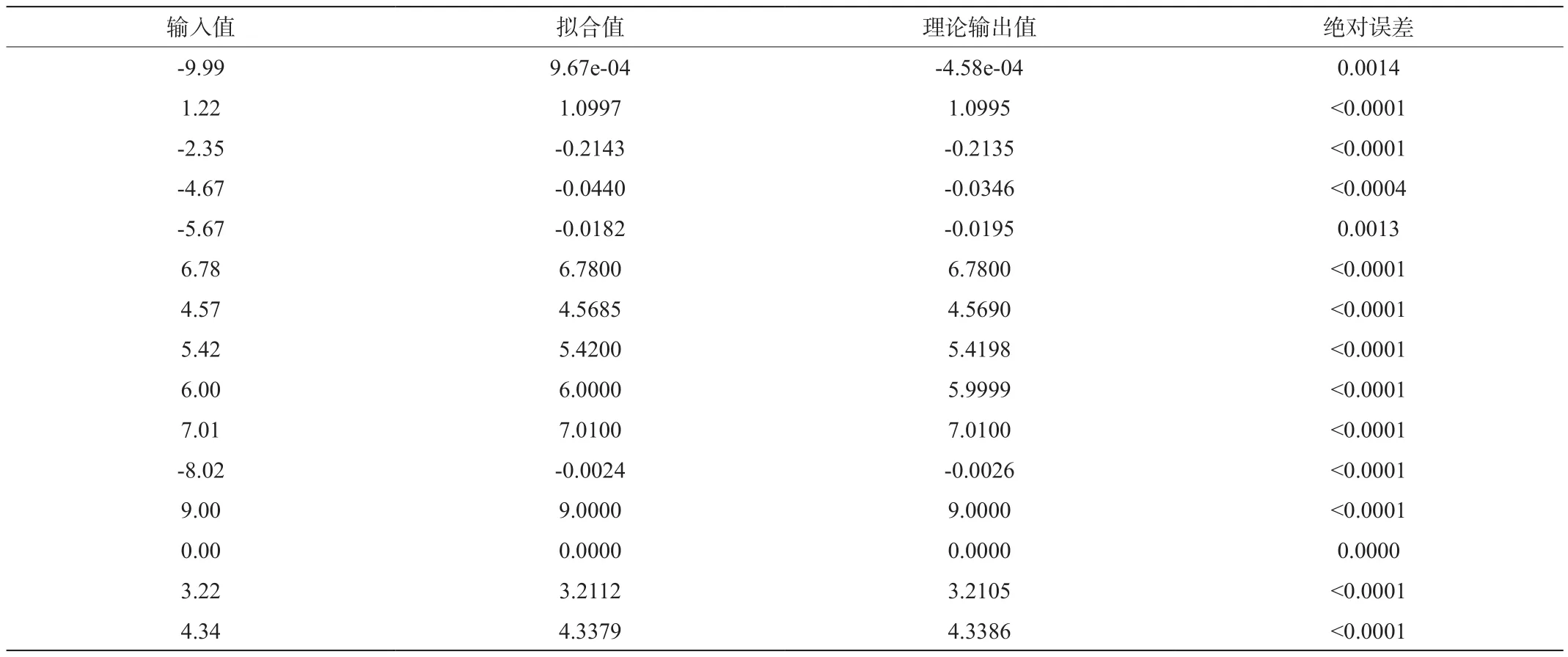
表4 Mish函数随机取点FPGA拟合结果

具体实现流程框图如下图3：

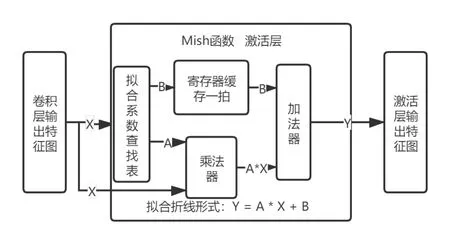
图4 Mish函数流程框图

由上图可以看出我们在卷积层输出特征后需要经过Mish激活函数,而激活函数具体实现是将拟合的多段折线系数存在查找表中，依据输入数据的大小，自动匹配对应的系数进行输出，输出查找表数据送入乘加器中实现激活函数拟合，最终输出结果。modulsim仿真结果如图4所示，我们可以看出完成一次拟合只需要三个时钟周期，第一个时钟通过查表取出对应的系数，第二个时钟周期用于系数与输入之间的乘法，第三个时钟则进行常数相加。因此在这种设计模式下只需要三个时钟周期即可完成一次输入输出。整体资源使用情况如图5所示，我们可以看到整体使用逻辑资源较少，而且每次激活运算只使用一个DSP资源。这对于神经网络加速来说是非常有利的。采用本文的设计方案在消耗较少资源的情况下可以实现较高的并行度，能更好地提升整体运算速度[9]。

图4 modulsim仿真结果

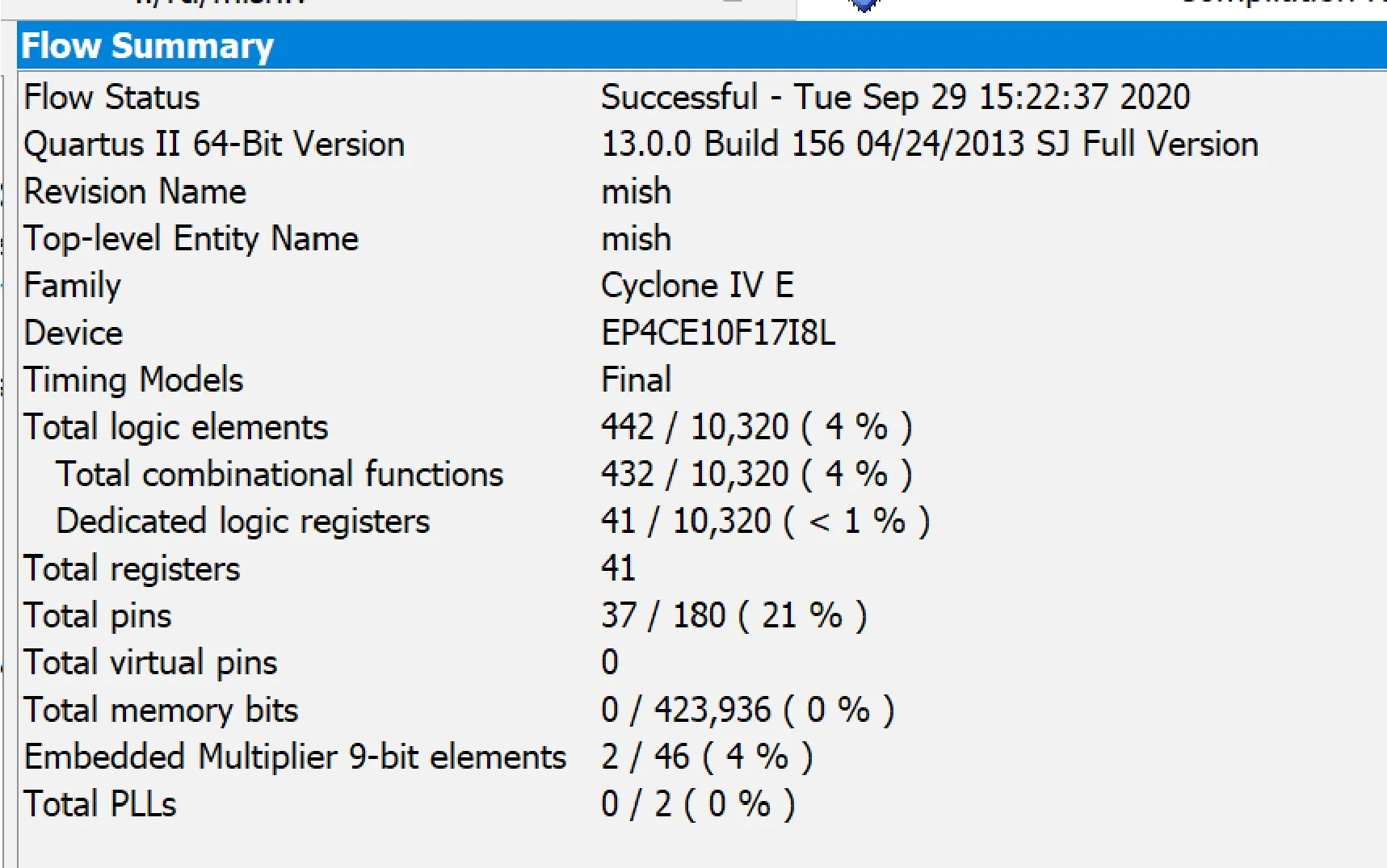
图5 FPGA实现Mish函数整体资源利用

4 结束语

YOLOv4及其衍生版本中，Mish作为激活函数是至关重要的一步，它的优异性能是其他激活函数无法替代的。欲使用FPGA加速YOLOv4及其衍生版本，则不可避免地要在FPGA上实现Mish函数。本文简单介绍了神经网络中常用的激活函数Mish，采用分段拟合的方式对该函数进行拟合并在FPGA平台上对其进行实现。对实现结果与实际结果进行误差分析，绝对误差控制在0.002以内，对神经网络输出结果不会产生影响。提出一种多折线拟合的方式实现Mish函数，所使用逻辑资源较少，运算速度快，适合在高并行度的神经网络中使用。对使用FPGA加速YOLOv4以及其他使用Mish函数作为激活函数的网络有一定的参考价值。