基于不同网格模型的机翼型架外形分步优化设计

张睿 崔德刚 裴志刚 袁武 李岩

摘要：机翼型架外形是机翼实际生产外形。型架外形结构设计中通常涉及结构强度优化和结构变形的迭代，两种分析考核的结构响应不同，适用的最佳网格密度也不同。基于同一网格模型完成诸如多目标的优化往往会造成精度不够、变形迭代无法收敛的情况。基于不同密度网格模型，采用分步优化策略，先通过反向迭代法得到自然网格模型下的初始型架外形，然后对此外形下的精细网格模型进行结构强度优化，将其优化结果映射至自然网格模型，基于自然网格模型完成型架外形的变形优化。最终确定的型架外形结果不仅满足强度要求，而且型架外形变形后与理想外形扭角分布也基本一致。

关键词：型架外形；复合材料结构优化；网格变量映射；遗传算法

中图分类号：V22文献标识码：ADOI：10.19452/j.issn1007-5453.2021.12.002

大展弦比民机机翼结构弹性较大，结构弹性变形对气动力的影响突出，同时民机进行长时间的巡航飞行，在巡航设计点需要较好的气动性能。因此，民机机翼需要进行型架外形设计，使得机翼在巡航状态即1g载荷下，变形至理想的巡航外形。

型架外形设计一般是基于理想巡航外形而进行的，通常是巡航外形反向加载[1]，得到初始的型架外形，然后初始型架外形正向加载变形后，再根据初始型架外形弹性变形后与理想巡航外形的差异进行型架外形的迭代修正。与此同时，机翼型架外形结构还要满足在2.5g载荷下的强度设计要求。

大展弦比机翼的型架外形设计涉及气动、结构以及气动同结构相互作用，国内外相关研究工作基本分成三类：一是研究气动力计算精度和引入方式对于型架外形设计的影响[2]；二是重点研究静气动弹性变形计算方法，先后发展了基于混合网格N-S方程和结构柔度矩阵方法[3]，CFD/CSD松耦合的三维机翼静气动弹性计算方法[4]，基于RBF径向基函数的气动弹性分析方法[5]等；三是以结构优化设计方法为主，是在型架外形确定的前提下，以机翼刚度分布和机翼弹性变形为优化目标，从而研究不同结构设计参数对于静气动弹性的影响。

在上述研究中，通常采用简化的梁模型或者特征尺寸较大的粗网格的板壳模型，以降低计算量并保证收敛性。此外，分析工况也多考虑1g载荷状态，无法满足实际结构强度设计工况规定，以及强度分析对于网格尺寸的要求。

型架外形设计最终得到的是一定外形下的結构模型，结构强度设计和分析要求采用较为精细的有限元网格模型，来提高应力应变的求解精度。而型架外形的变形迭代修正涉及有限元模型节点的几何修正，收敛判据无论是全网格节点的匹配还是若干剖面的几何匹配，过多数量的网格会造成计算局部奇异导致无法收敛。研究者也曾采用B样条插值[6]，仅考虑有限个剖面的节点迭代收敛，其余弦向和展向的节点通过插值来确定，但同样网格数量不能太多，否则会造成插值计算量过大。

考虑型架外形设计中外形迭代和结构优化所适用的模型网格尺度和必须基于的载荷工况，以及已有设计方法中的并未在同一流程中基于两个专业适用的分析模型和工况完成相应的设计。本文提出一种基于不同密度网格模型的型架外形分步优化策略，先通过反向迭代法得到自然网格模型下的初始型架外形，然后以其外形下的精细网格模型进行结构强度优化设计，将其优化结果映射至自然网格模型，最终基于自然网格模型完成型架外形的变形优化迭代，设计流程如图1所示。在图1所示的流程中，自然网格下型架外形设计是基于1g载荷工况下自然网格模型，考验在巡航状态下结构能否变形至理想巡航外形，强度优化是2.5g载荷工况的精细网格模型，优化以结构重量最小为优化目标，结构应力为约束目标，最终确定的型架外形结果不仅满足强度要求，而且型架外形变形后与理想外形扭角分布也基本一致。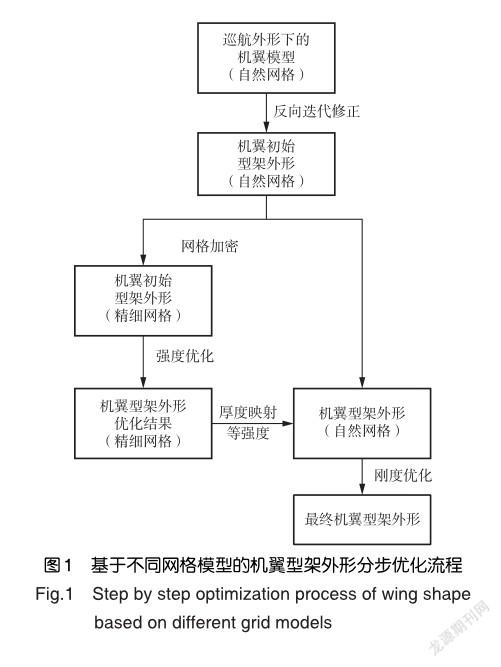

1研究方法

1.1完全解耦的初始型架外形设计

自然网格下初始型架外形的迭代修正采用Sherif等[7]提出的一种完全解耦的机翼型架外形设计方法，如图2所示。

该方法将型架设计分为两层，第一层为计算流体力学（CFD）分析，即为了确定理想巡航外形的气动力计算，并将确定的外形输出至第二层分析，因为巡航外形在巡航工况下计算得到的定常气动载荷分布就是气动与结构耦合作用稳定状态下的气动力；第二层为结构有限元分析，主要是基于第一层的理想外形进行结构的形状优化，该层只进行结构有限元分析，不再进行气动力计算，一直使用理想巡航状态气动力，优化结束后输出型架外形。最后只需对型架外形弹性变形后的一些气动特性参数进行校核。

在自然网格模型下，基于Aly方法采用如下步骤来获得初始的型架外形：（1）调用CFD求解器，计算飞机巡航外形下的气动特性；（2）通过Aly的方法确定型架外形J0；（3）将巡航外形下的所有的气动力、惯性力等载荷正向加载至型架外形J0，来计算型架外形的变形；（4）比较巡航外形和型架外形变形后每个结构节点的位移差Δy；（5）修正型架外形结构节点，修正量为γΔy，γ为修正系数，0<γ<1，得到更新后的型架外形；（6）如果Δy<误差阈值epsilon，则流程结束，否则返回至第（3）步。

上述迭代过程只涉及结构有限元模型的更新，气动载荷为理想巡航外形下的载荷。

1.2结构静强度优化

静强度优化是通过调整初始型架外形下的复合材料蒙皮参数，使得型架外形在2.5g载荷下满足强度要求，并且重量最轻。静强度优化基于精细网格模型，一方面是由于网格加密能够提高应力分析的精度；另一方面，网格密度的增加使得设计单元增加，从而提高了设计变量空间，能够得到更好的优化设计结果。

1.2.1优化问题的定义

本文中采用一种逐步增加厚度尺寸的优化策略，设计单元的厚度是从最小的厚度开始进行优化，相应的设计变量是从可行域外部趋向于最优解Xˉ，显然满足外罚函数的定义。

1.2.2基于KS函数约束的缩聚

应力/应变约束是与结构有限元中单元个数同量级的，对于精细网格模型，约束可达到上万量级，即gi（x）的个数。对于如此大规模约束优化问题，必须引入约束缩聚的方法，才能利用优化方法进行求解。在飞行器结构优化中，KS函数被广泛用于应力应变等局部约束的缩聚[10-12]。

KS函数由Kreisselmeier和Steinhauser在1979年提出[13]，最先应用于控制领域。KS函数重新定义了设计变量的可行域，该可行域比原始约束定义的可行域更小，即建立了关于最大约束的保守估计的包络面。

1.2.3优化算法

遗传算法是基于达尔文进化理论和孟德尔遗传学说形成的算法，它是一种自适应的全局优化的概率搜索方法，最早由美国密执安大学的Holland教授提出，起源于60年代对自然和人工自适应系统的研究[16]。1985年，在美国召开第一届遗传算法国际会议，并且自成立国际遗传算法学会起，人们对遗传算法进行了广泛深入的研究，在复合材料铺层优化方面也取得了很多进展[17-19]。

遗传算法需要首先设置种群大小、染色体长度、解码规则、选择交叉变异概率。实际优化中先根据设计变量的取值范围随机投点生成遗传算法的种群，然后根据种群中个体的染色体解码后得到的设计参数，修改模型文件，再提交求解器计算出个体模型的适应度，最后执行精英保留、选择、交叉、变异等常规操作。不同于数值优化，涉及工程模型的优化，必须根据种群个体的解码结果实时地更新模型文件，這样才能获得遗传算法所需的个体适应度（目标函数响应），本文的遗传算法部分通过C语言编码实现。

1.3变形优化

变形的优化是在满足静强度要求的型架外形模型上，重新对型架外形在1g载荷下的蒙皮铺层刚度进行优化设计，以满足变形后与巡航外形之间的形状控制要求。在初始型架外形的迭代中，对机翼的弯曲和扭转都进行了修正，在这步优化中，只考虑剖面扭转角与巡航外形分布的偏差。

1.3.1优化问题的定义

目标函数计算出型架外形变形后节点y向坐标与理想巡航外形差距最大值，然后最小化该差量，一般当f

迭代过程中的型架外形变形后与理想巡航外形节点坐标差最大值Δy变化如图9所示，通过16步的迭代就可以满足收敛判据（Δy<1）。

3.2型架外形静强度优化

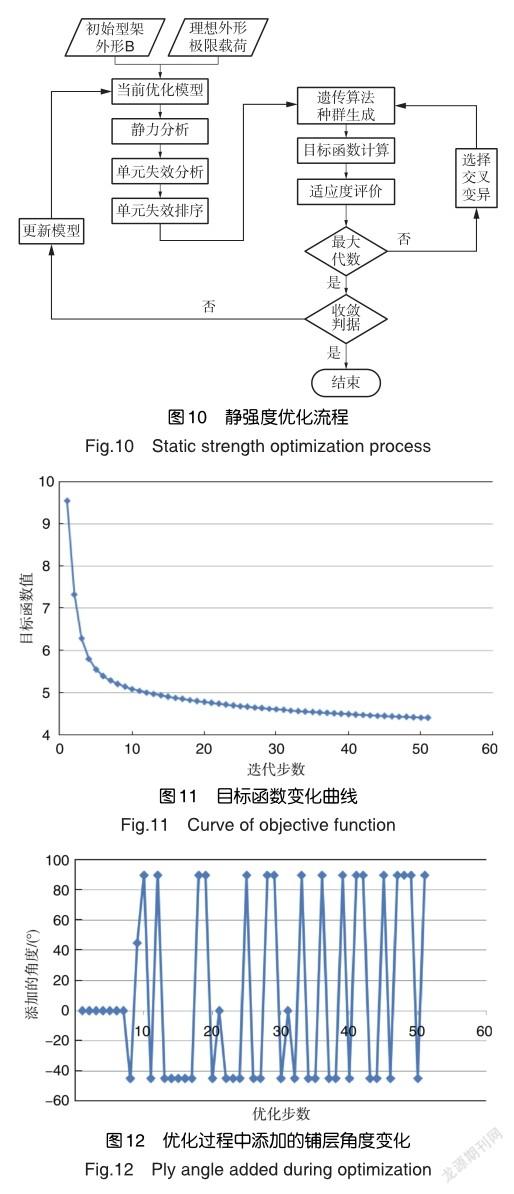
在初始型架外形下，对机翼结构网格进行加密，得到型架外形下的精细网格结构有限元模型，在此模型下的静强度优化流程如图10所示。

图11为精细网格模型的静强度优化结果，目标函数随着优化步数的增加在逐渐降低，前30步目标函数下降较快，因为大部分的单元应变较高，增加铺层厚度后，应变降低显著，随着优化的进行，大部分单元的应变小于许用应变后，目标函数下降趋势减缓。

图12为优化过程中每一步增加的铺层的铺层角度，其中0°铺层占17.6%，-45°铺层占47%，90°铺层占33%，主要是增加垂直纤维方向的抗拉压强度，以及单元的剪切强度。

优化初始，翼根、机翼中部位置厚度增加比较显著。此外，厚度增加都是在翼肋附近，主要是因为机翼中部翼肋上有前后缘较大的集中载荷，造成局部应变较高，优化后的机翼上下蒙皮厚度分布如图13所示。

优化后精细网格模型的结构质量为1994kg，理想巡航外形下自然網格模型结构质量为2168.3kg，实现结构质量减小8.04%。

3.2.1网格厚度变量映射

将精细网格模型的单元厚度映射至型架外形下的自然网格模型上，映射结果如图14所示。由于蒙皮铺层还涉及铺层角度，因此在得到自然网格模型的节点厚度后，在精细网格模型的单元铺层中进行搜索，匹配与之厚度最为接近的铺层厚度，将对应的铺层属性（包含厚度角度信息）赋予自然网格的单元。

厚度变量映射会造成结构质量的变化，映射后结构质量略有增加，约为0.6%。

3.2.2变形优化

满足2.5g强度要求的型架外形，由于结构刚度的重新分配，该型架外形在1g载荷下无法变形至理想巡航外形，需要在静强度优化结果基础上进一步以变形为目标进行优化。

对优化后的机翼模型沿展向共选取5个剖面，根部剖面为参考剖面，图15给出了不同外形下展向5个剖面的扭转角分布情况。蓝色实心点线为理想巡航外形的扭转角分布，红色加号线为初始型架外形下的扭转角分布，即通过反向迭代设计得到的型架外形的扭转角分布。初始型架外形变形后在内翼段剖面扭转角基本与巡航外形重合，外翼段剖面扭转角最大误差为0.62°。绿色三角形代表经过强度优化后的（满足2.5g过载设计）型架外形变形，由于强度优化时，厚度主要增加在机翼中部位置，位于展向剖面1～3之间，造成机翼刚轴前移，加剧了翼尖的负扭转，而通过最后一步基于型架形的变形优化后，机翼外段后缘增加了厚度，使得刚轴后移，抑制了翼尖负扭转，从而各剖面的扭转角与理想巡航外形下的角度基本保持一致，最大扭角度误差为0.08°，基本对机翼气动特性不会产生影响。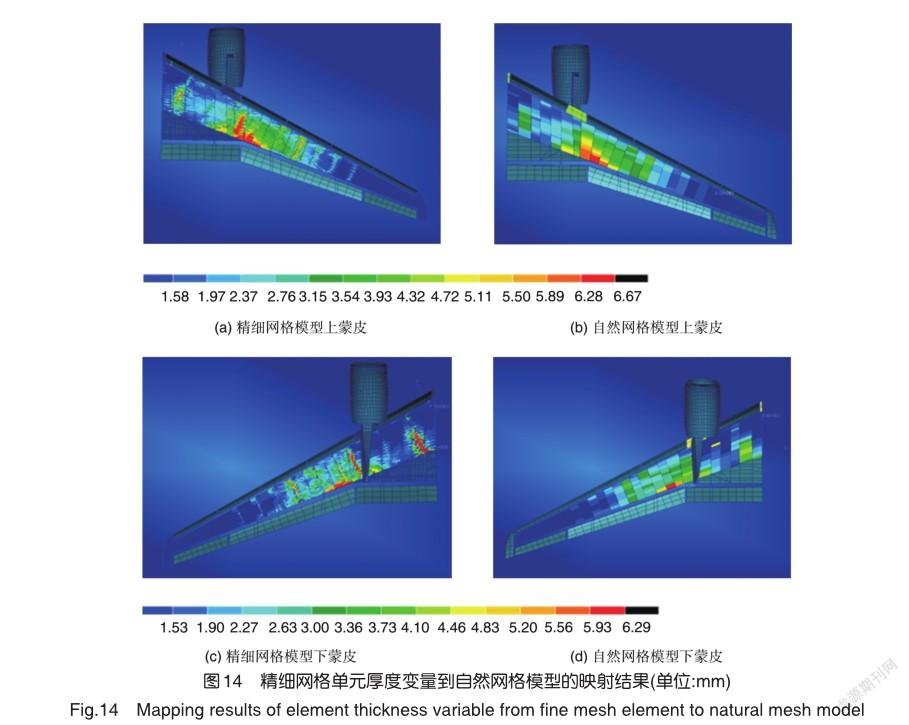

4结论

本文基于不同密度网格模型，采用分步优化策略，先通过反向迭代法得到初始型架外形，然后以其外形下的精细网格模型进行结构强度优化设计，将其优化结果映射至自然网格模型，基于自然网格模型完成型架外形的变形优化，研究结论如下：

（1）基于不同网格模型的分布优化策略，既能满足强度优化的网格量级要求，得到满足强度要求的最轻结构质量，又能避免因网格数量过多，造成变形迭代收敛困难。

（2）在初始型架外形确定阶段，结构反向迭代修正设计能够快速得到收敛的型架外形，并且该型架外形变形后的气动特性与理想巡航外形保持一致。

（3）通过精细网格模型的设计，采用大规模变量的优化，更能减轻结构质量，单个机翼结构质量减小了8.04%。

（4）基于等参元逆变换的网格变量映射方法能够将精细网格模型的厚度变量映射至自然网格模型，但由于复合材料铺层的特殊性，还需对铺层角度进行处理，映射后，整个机翼结构质量的变化约为0.6%，厚度映射较为准确。

（5）满足2.5g载荷设计的型架外形在1g载荷下无法变形至理想巡航外形，通过变形优化设计可以使型架外形变形回理想巡航外形。最终确定的型架外形变形后与理想巡航外形的剖面扭转角基本保持一致，最大角度误差为0.08°。

参考文献

[1]程诗信，詹浩，朱军.考虑气动弹性影响的机翼气动外形设计研究[J].航空计算技术，2008，38（2）：37-39. Cheng Shixin， Zhan Hao， Zhu Jun. Study on aerodynamic and aeroelastic integrated design method for wing[J]. Aeronautical Computing Technique， 2008，38（2）：37-39. （in Chinese）

[2]谢萌，程攀，薛飞.基于不同CFD方法的机翼型架外形设计分析[J].民用飞机设计与研究，2011（4）：16-17. Xie Meng， Cheng Pan， Xue Fei. Design and analysis of wing jig-shape by different CFD methods[J]. Civil Aircraft Design and Research， 2011（4）： 16-17. （in Chinese）

[3]Wan Z Q，Liang L，Yang C. Method of the jig shape design for a flexible wing[J]. Journal ofAircraft，2014，51（1）：327-330.

[4]杨国伟，郑冠男.基于静气动弹性效应的飞机型架外形修正方法研究[J].航空工程进展，2011，2（2）： 143-150. Yang Guowei， Zheng Guannan. Aircraft jig shape correction method based on static aeroelastic analyses[J]. Advances in Aeronautical Science and Engineering， 2011，2（2）： 143-150.（in Chinese）

[5]Sherif A，Madara O，Richard P，et al. Jig-Shape static aeroelastic wing design problem：a decoupled approach[J]. Journal ofAircraft，2002，39（6）：1061-1066.

[6]Gaetan K，Joaquim M，Graeme K. Aerostructural optimization of the common research model configuration[C]//58th AIAA/ ASCE/AHS/Structures，Structural Dynamics，and Materials Conference，2017.

[7]Sherif A，Madara O，Richard P，et al. A decoupled stochastic approach to the jig shape aeroelastic wing design problem[C]// 36thAerospace Sciences Meeting & Exhibit，1998.

[8]雷國东，李岩.跨声速飞机高可信度多设计点多约束气动优化设计技术研究[J].航空科学技术， 2019， 30（9）： 9-18. Lei Guodong， Li Yan. Research of the multiple design-points high-fidelity aerodynamics optimization technologies for the transonicaircraft with the multiple constraints[J]. Aeronautical Science & Technology，2019，30（9）： 9-18. （in Chinese）

[9]陈宝林.最优化理论与算法[M].北京：清华大学出版社，2005. Chen Baolin. Optimization theory and algorithm[M]. Beijing： Tsinghua University Press， 2005. （in Chinese）

[10]兆文忠. KS函数与最小-最大优化问题[J].大连铁道学院学报， 1992，13（2）：16-21. Zhao Wenzhong. KS function and optimization of min-max problem[J]. Journal of Dalian Institute of Railway Technology， 1992，13（2）： 16-21. （in Chinese）

[11]粟华，谷良贤，龚春林.基于KS函数的协同优化算法及其应用[J].航空制造技术，2011（6）： 86-88. Su Hua， Gu Liangxian， Gong Chunlin. Collaborative optimization based on KS function and its application[J]. Aeronautical Manufacturing Technology， 2011（6）：86-88. （in Chinese）

[12]张科施，韩忠华，李为吉，等.基于近似技术的高亚声速运输机机翼气动/结构优化设计[J].航空学报，2006，27（5）：810-815. Zhang Keshi， Han Zhonghua， Li Weiji， et al. Multidisciplinary aerodynamic/structural design optimization for high subsonic transportwingusingapproximationtechnique[J].Acta Aeronautica et Astronautica Sinica， 2006，27（5）：810-815. （in Chinese）

[13]Kreisselmeier G，Steinhauser R. Systematic control design by optimizing a vector performance index[J]. IFAC Proceedings Volums，1979，12（7）：113-117.

[14]Bret S，Christine J，Carol W. Trim and structural optimization of subsonic transport wings using nonconventional aeroelastic tailoring[J].AIAAJournal，2016，54（1）：293-309.

[15]Nicholas P，Joaquim M. An adaptive approach to constraint aggregationusingadjointsensitivityanalysis[J].Struct Multidisc Optim，2007，34：61-73.

[16]Holland H. Adaptation in nature and artificial system[M]. Cambridge：MIT Press，1992.

[17]馬博平，王刚，叶坤，等.基于RBF神经网络和遗传算法的超声速Licher双翼优化设计研究[J].航空科学技术，2019，30（9）：73-80. Ma Boping， Wang Gang， Ye Kun， et al. Supersonic licher biplane optimization using radial-basis function neural network and genetic algorithm[J]. Aeronautical Science & Technology，2019，30（9）：73-80. （in Chinese）

[18]程文渊，崔德刚.基于Pareto遗传算法的复合材料机翼优化设计[J].北京航空航天大学学报，2007，33（2）： 145-148. Cheng Wenyuan， Cui Degang. Optimization for composite wing based on pareto genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics， 2007， 33（2）： 145-148. （in Chinese）

[19]王晓军，马雨嘉，王磊，等.飞行器复合材料结构优化设计研究进展[J].中国科学：物理学、力学、天文学， 2018， 48（1）： 22-37. Wang Xiaojun， Ma Yujia， Wang Lei， et al. Advance in the optimization design study for aircraft composite structure[J]. Science China Physics， Mechanics & Astronomy， 2018， 48（1）： 22-37. （in Chinese）

[20]王凯剑，张睿，李岩.翼身融合客机PRSEUS壁板参数识别研究与优化设计[J].航空科学技术， 2021， 32（5）： 44-53. Wang Kaijian， Zhang Rui， Li Yan. Parameters identification research and optimization design of PRSEUS panel in blendedwing-bodycivilaircraft[J].AeronauticalScience& Technology，2021， 32（5）： 44-53. （in Chinese）

[21]刘迪辉，李光耀，李洪周，等.一种用于汽车碰撞模拟的网格变量映射算法及其验证[J].机械工程学报，2009，45（12）：

218-223. Liu Dihui， Li Guangyao， Li Hongzhou， et al. Mesh variables mapping algorithm used in car crash simulation and its verification[J]. Journal of Mechanical Engineering， 2009， 45（12）： 218-223. （in Chinese）

[22]朱以文，李伟，蔡元奇.基于解析性质的等参有限元逆变换高效算法[J].武汉大学学报，2002，35（2）：62-65. Zhu Yiwen， Li Wei， Cai Yuanqi. An efficient inverse isoparametric mapping in fem based on analytical character[J]. Engineering Journal of Wuhan University， 2002，35（2）：62-65.（in Chinese）

[23]李洲，杨旭静.网格变量映射方法在有限元分析中的应用[J].汽车工程， 2012， 11（34）： 1049-1053. Li Zhou， Yang Xujing. The application of mesh variables mapping to finite element analysis[J]. Automotive Engineering， 2012， 11（34）： 1049-1053. （in Chinese）

Stepwise Optimization Design of Wing Jig Shape Based on Different Grid Models

Zhang Rui1，Cui Degang2，Pei Zhigang3，Yuan Wu4，Li Yan1

1. Chinese Aeronautical Establishment，Beijing 100012，China

2. Science and Technology Committee of Aviation Industry Corporation of China，Beijing 100012，China

3. AVIC Shenyang Aircraft Design & Research Institute，Shenyang 110035，China

4. Chinese Academy of Sciences，Beijing 100190，China

Abstract： The jig shape is the actual production shape of the wing. The optimization of structural strength and the iteration of structural deformation are usually involved in the jig shape structure design. The structural responses derived from two analysis processes are different， so as the optimal grid model density for the two processes. A multiobjective optimization based on the same mesh model usually results in that the accuracy is not enough and the deformation iteration cannot converge. Based on different density grid models， a stepwise optimization strategy is adopted. First， the initial wing jig shape is obtained by the reverse iteration method. Then， the structural strength is optimized by using the fine mesh model under the jig shape. The optimization results are mapped to the natural grid model， and the deformation optimization of the jig shape is completed based on the natural grid model. The final jig shape can not only meet the strength requirements， but also the twist angle distribution of the wing after deformation is basically consistent with the ideal shape.

Key Words： jig shape； composite structure optimization； grid variable mapping； genetic algorithm