基于有限元方法的CeCl3 和NdCl3 在LiCl-KCl熔盐中的电极动力学模拟
2021-02-02顾徐波周文涛王德忠
顾徐波,周文涛,王德忠
(上海交通大学,上海200240)
随着核电的大规模应用, 乏燃料的妥善处理已经是中国乃至全世界核电发展中亟待解决的问题。乏燃料是经过反应堆辐照后的核燃料, 其主要成分是铀和钚等锕系元素以及各种裂变产物, 其中裂变产物中含有大量的镧系元素。 乏燃料熔盐电解后处理技术由于具有诸多优点(如设备紧凑、二次放射性废物少、耐辐照性好、临界事故发生几率低等),受到国内外广泛关注[1-2]。 典型的熔盐电解分离以LiCl-KCl 熔盐为电解质,通过电位控制和电极转换,达到元素分离的目的。 锕系元素和镧系元素由于电化学性质相近,是熔盐电解后处理研究的重点和难点。只有充分理解锕系元素和镧系元素在熔盐中的行为和性质,才能提高锕系、镧系元素之间的分离率。 熔盐电解实验需要在高温和具有腐蚀性的熔盐条件下进行,部分乏燃料元素甚至还具有强放射性,这些都限制了实验的广泛开展[3]。 因此,通过模拟手段分析元素在熔盐电解过程中的行为具有重要意义,可以大量减少实验时间和资金投入。目前,国外已经有一些相关的文献报道:S.H.Kim 等[4]利用有限元软件 Comsol分析了铀的电化学沉积行为, 评价了实验室级别的电解精炼单元性能, 较好地模拟了铀的沉积行为;W.Zhou 等[5-6]结合流场条件、扩散方程和电子转移动力学开发了乏燃料在熔盐中转移的整体模型,并用实际案例论证了其模型的准确性, 能够较好地预测锕系元素和一些主要的镧系元素在电解精炼过程中的转移过程。国内的相关文献报道较少,对于元素在熔盐中的数值模拟研究还处于起步阶段。 张萌等[3]利用Comsol 模拟了铀在熔盐中阴极上的沉积行为,并分析优化了最佳阴极位置,为电解精炼器的设计提供依据,同时也模拟了铈离子在LiCl-KCl 中的电化学行为和电沉积行为, 较为全面地分析了铈离子在熔盐中的行为与性质[7]。 然而,研究只进行了单一工况的模拟, 缺乏对离子在熔盐中行为模拟的普适性论证,也缺少对某些多步骤还原离子的研究。本文采用Comsol 针对铈离子和钕离子开展研究,其中钕离子的还原过程是一个两步骤的过程, 模拟了不同浓度和温度下两种镧系元素的循环伏安曲线,并与实验数据做了对比,结果表明,有限元模拟能够准确地反映实际电极还原过程。 由于乏燃料中绝大部分元素在LiCl-KCl 熔盐中都是单步骤或二步骤还原,因此模拟可以涵盖大部分元素的还原行为,为乏燃料元素在熔盐中的性质获取提供了低成本且可靠的方法。
1 电化学电极过程动力学模型
考虑一根电极插入熔盐电解液中发生电化学反应,如图1 所示。 熔盐电解液由LiCl-KCl 以及被分析的盐组成,图中用一般代表意义的氧化物表示被分析的盐。 x=δ 代表扩散层厚度边界,x=0代表电极表面。
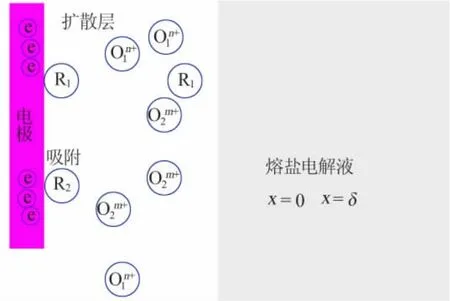
图1 元素在熔盐中的电化学过程示意图

还原物R1可溶,因此会向熔盐电解液中扩散,而还原物R2是固体,吸附于电极表面。
发生反应后,电极表面的离子浓度降低,与熔盐电解液中离子的浓度之间存在浓度差,产生扩散。离子的扩散方程由菲克第二定律描述:

式(3)中, Ci为第 i 种离子的浓度;Di为第 i 种离子的扩散系数。
采用Bulter-Volmer 公式来描述电极上电流与施加电位之间的关系,电极上电流密度:
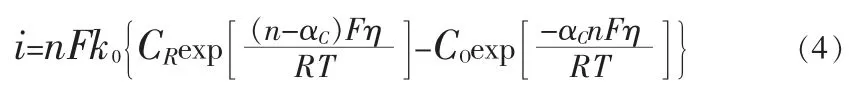
式(4)中,F 是法拉第常量;αC是阴极传递系数;R 是理想气体常数;T 是开尔文温度;k0是标准速率常数;CR和CO分别代表还原物和氧化物的浓度;η 是过电位,是电极施加电位与平衡电位之差:

Bulter-Volmer 公式作为扩散方程在x=0 处的边界条件。
在 x=δ 处的边界条件由式(6)和式(7)描述:

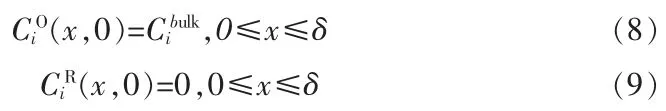
2 结果与讨论
2.1 CeCl3 的模拟结果与讨论
循环伏安法(CV)是一种用于研究电化学过程十分常用的方法。 图2 为CV 中施加的电位信号图和典型的循环伏安响应图[8]。 其中前向扫描时,物质发生还原反应,产生还原峰(阴极峰),后向扫面时物质发生氧化反应,产生氧化峰(阳极峰)。 利用CV 曲线中的阴极峰峰位信息,应用Berzins 和Delahay 公式可以计算元素在熔盐中的扩散系数、 形式电位等重要参数[9-10]。因此本文中也主要考虑模拟结果的阴极峰信息与实验结果的吻合程度。
CeCl3在LiCl-KCl 熔盐中发生一步3 电子的还原过程, 铈离子得到3 个电子后还原为金属铈吸附于电极表面:

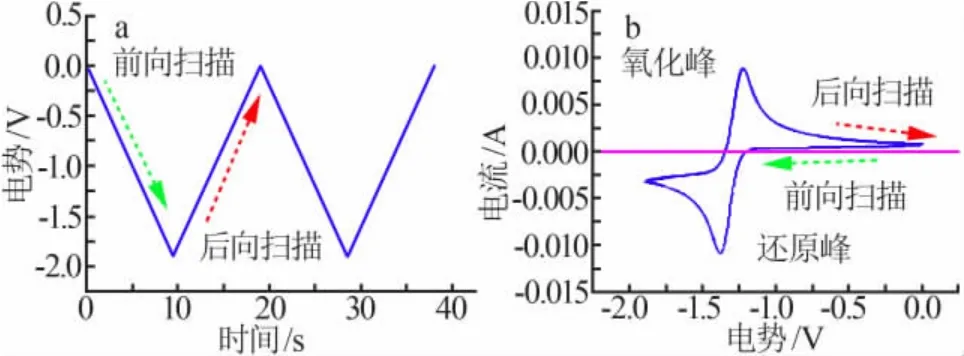
图2 循环伏安法中施加电位信号图(a)典型的循环伏安响应(b)[8]
表1 是CeCl3模拟中的输入参数。
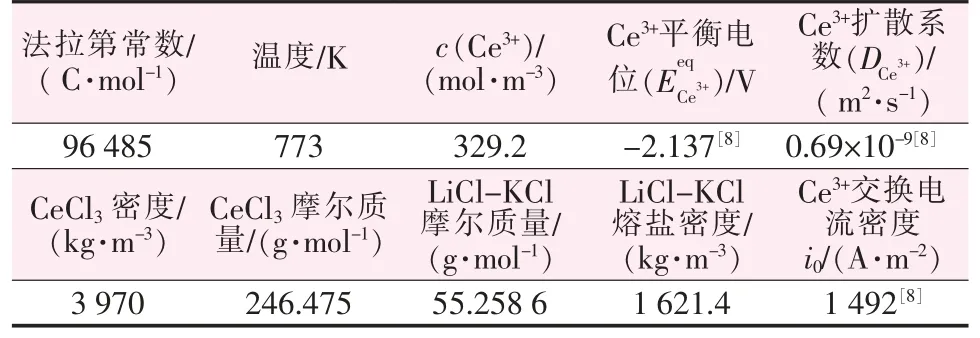
表1 CeCl3 模拟中的输入参数
图3a 是质量分数为0.5%、温度为773 K、扫描速率为50 mV/s 条件下的CeCl3的模拟结果和实验结果对比图,实验结果参考文献[8]。从图3a 可以观测到Comsol 有限元模拟所得的循环伏安曲线阴极峰峰电位和峰电流与实验结果吻合度高, 表明模拟的结果是可靠的。 不过模拟和实验结果之间在峰前和峰后仍然存在差异。首先是在峰前位置,与实验相比, 模拟的还原起始位置更正, 这可能是由于在Comsol 模拟中把还原物质Ce 设置成了可溶物,其扩散系数相比 Ce3+小 10 个量级(0.69×10-19m2/s),这可能造成了在模拟时, 电极表面第一层网格的还原物浓度偏小。 根据能斯特方程,Ce3+/Ce 反应之间的平衡电势可以按下式描述:
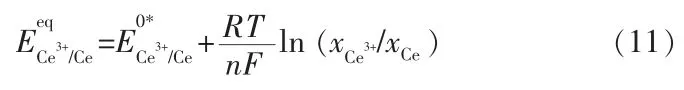
在峰后位置,实验的电流要比模拟结果更大。这可能是吸附成核导致的, 在实验中由于吸附过程的存在,会产生非法拉第电流,即不是因为电子转移而产生的电流,非法拉第电流会叠加在法拉第电流上。但是在模拟中只考虑了因为电子转移产生的法拉第电流,从而会导致模拟值比实验值小的现象。在峰值后, 电极表面沉积的金属较多, 吸附过程则更为明显,两者的差距相对于峰值前更大。
为验证不同浓度和温度下模拟的可靠性, 改变CeCl3的浓度以及温度条件后进行模拟, 结果如图3b 和图3c 所示。 其中图3b 是将质量分数增至2%时的结果,图3c 是温度增至833 K 和质量分数增至1.82%时的模拟结果。 图3b 和图3c 的实验数据分别参考文献[8]和[11]。表 2 列出了 3 组模拟和实验的数据对比。 从图3b 可以得知,改变浓度后模拟的结果依然与实验结果十分吻合, 表明模型能够模拟不同浓度的CeCl3的电化学过程。 图3c 中的模拟与实验差距相比前两次模拟要大,由表2 可以看出,这组实验的阴极峰电流相对误差在0.12, 误差变大的原因可能是由于模拟的参数主要依据文献[8],而不同的实验之间[8,11]由于存在盐的纯度、电极材料、实验环境等差异,结果亦存在一定的差异性。

图3 模拟结果与实验对比图[参比电极:5%(物质的量分数)Ag/AgCl](a、b)及模拟结果与实验对比图(参比电极:1%Ag/AgCl)(c)
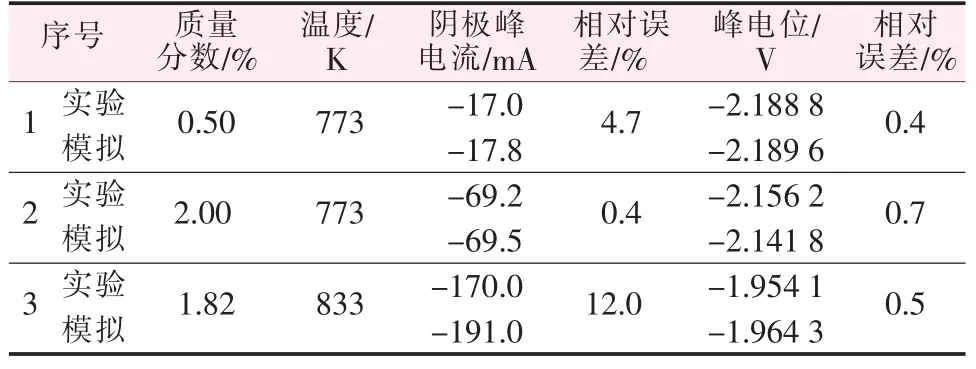
表2 CeCl3 模拟结果与实验比较
2.2 NdCl3 的模拟结果与讨论
NdCl3在LiCl-KCl 熔盐中的模拟特点和难点在于还原是分为两步进行的,Nd3+首先得到一个电子还原为Nd2+,电极表面的Nd2+得到2 个电子后还原为金属Nd,其中Nd2+是可溶的,会向熔盐电解液中扩散:

按照第一章节中建立的模型,将其应用于NdCl3需要分别对Nd3+和Nd2+建立相应的扩散方程,以及相应的边界条件和初始条件。
表3 是NdCl3模拟中的参数输入。

表3 NdCl3 模拟中的输入参数
在不同温度和浓度下对NdCl3的还原过程进行模拟,图4 是质量分数为3%、温度为723 K、扫描速率为40 mV/s 条件下的模拟和实验结果。 由图4 可以看出,二者吻合度较高。图5 是改变浓度或温度情况下的模拟和实验结果(实验结果参考文献[12])。表4 统计了3 组模拟和实验数据对比, 包括Nd3+还原为Nd2+以及Nd2+还原为金属Nd 的峰电流和峰电位信息,以及相对误差。 从表4 可知,阴极峰电流模拟和实验的相对误差分布在0~0.075, 峰电位的误差分布在0.004~0.008,表明模型模拟不同浓度和温度下NdCl3在LiCl-KCl 熔盐中电化学过程的可靠性。 在Nd 的模拟中,没有像Ce 那样存在起始还原位置差异,这是因为还原物Nd2+本身就是可溶的,其扩散系数等参数可以被较为准确地定义。
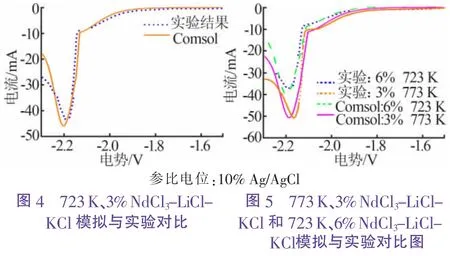

表4 NdCl3 模拟结果与实验比较
3 结论与展望
本文利用有限元方法分别模拟了不同浓度和不同温度下CeCl3和NdCl3在LiCl-KCl 熔盐中的循环伏安曲线, 结果表明建立的模型在不同浓度和温度下能够较为准确地反映乏燃料元素在熔盐中的电化学过程, 为元素在熔盐中的性质获取提供了低成本且可靠的方法。
模拟和实验结果之间在峰前和峰后仍然存在差异。 后续研究中需要考虑如何以更加合理的方式定义电极表面的金属, 同时也需要考虑成核等电极表面因素,进一步完善边界条件的表述。
