等差法解答一类走走停停行程问题

苏蕤轩

(四川省成都欧拉教育 611430)

一、引入

在很多小学毕业考试、小学杯赛或初中数学考试中常出现行程问题，它是普遍学生的弱项，同时也成为命题者偏爱的题型之一，在奥数竞赛中拥有非常显赫的地位.走走停停行程问题属于难点题型，它并不能直接用基本行程公式解决，需要经过复杂的判断和计算，已有文献给出了路程差是休息路程整数倍时的解答方法，但是该方法并不能解决路程差不是休息路程整数倍的题型.本文重在于探索一种更具有通用性的方法.

二、难点突破

此类问题的难点在于如何判断最终状态，本文通过等差数列和斜率来突破难点，通过平移快者的路程来计算追及时间.

1.最终状态判断

本文把题目给定的路程差用S表示，休息路程用ΔS表示，休息时间用ΔT表示，快者的速度用vk表示，慢者的速度用vm表示.

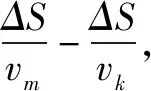
最终追及点判断需要明确到底是快者追及上行进中的慢者还是休息中的慢者.本文将结果分为如下三类：

(1)快者最后一次休息后的行进中，第一次追及上行进中的慢者；

(2)快者最后一次休息后的行进中，第一次追及上休息中的慢者；

(3)快者最后一次休息前的行进中，第一次追及上行进中的慢者.

图1

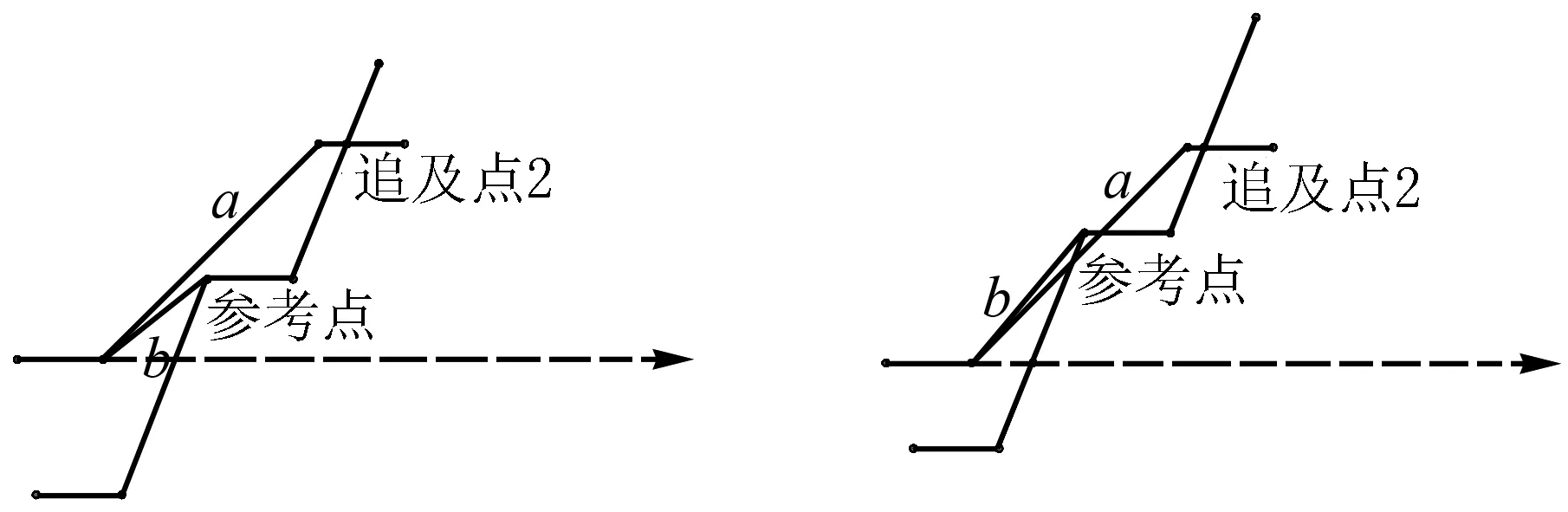
图2

判断好斜率后，如果b斜率小于a，就还要判断追及点会不会在慢者的休息区，因为排除了类型(3)，还得锁定到底是(2)还是(1)，所幸这比较容易，比较下一个休息区的时间差即可.

如果是类型(2)，那么：公差-余数<休息时间，如果是类型(1)，那么：公差-余数>休息时间，见图3，标注的横线部分就是“公差-余数”.

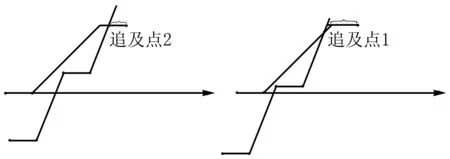
图3

2.追及时间计算

如果是类型(1)和类型(3)，可优先使用平移快者的方法，快速得到连续追及的时间，我们假定追及上时快者比慢者多休息Δn次，那么连续追及时间为(S+Δn×ΔT×vk)÷(vk-vm)，这个时间恰好等于慢者的连续行进时间，外加慢者的休息时间即为总的追及时间.

如果是类型(2)，直接通过慢者计算即可.假定慢者一共休息了n次(含最后一次)，因为最后一次没有休息完，离休息结束还有“公差-余数”，所以直接当成n次计算总时间，然后减去“公差-余数”即可.

三、典例分析

例1 快慢两人分别从相距550米的两地同时出发同向而行，他们每走200米都会停1秒，已知快者的速度是100米每秒，慢者的速度是40米每秒.求快者第一次追上慢者的时间.

解答：快者行至路程差的时间外加休息时间550÷100+2×1=7.5秒

次数7.5÷3=2次……1.5秒

(50是快者的休息区跟慢者前一次休息区的距离，因为200的倍数减去550，最小值为50)

下一次的余数3-1.5=1.5秒，大于1秒

属于类型①，接下来平移快者，直接计算追及时间

例2快慢两人分别从相距550米的两地同时出发同向而行，他们每走200米都会停1秒，已知快者的速度是100米每秒，慢者的速度是60米每秒.求快者第一次追上慢者的时间.

解答：快者行至路程差的时间外加休息时间为：550÷100+2×1=7.5秒

快者已经休息2次

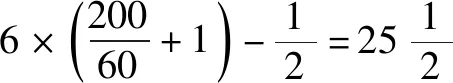
例3快慢两人分别从相距500米的两地同时出发同向而行，他们每走200米都会停1秒，已知快者的速度是100米每秒，慢者的速度是60米每秒.求快者第一次追上慢者的时间.

解答：快者行至路程差的时间外加休息时间500÷100+2×1=7秒

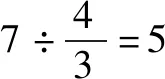
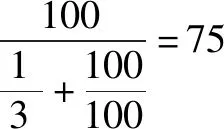
属于类型③，接下来平移快者，直接计算追及时间

处理此类休息路程相同的走走停停行程问题可以按照如下思路解决：其一、通过两者行进休息路程的时间差计算休息次数；其二、通过斜率判断属于哪种类型；其三、直接计算(类型②)或通过平移法计算(类型①或类型③)追及时间.