柔性人行天桥舒适度的评价分析
2021-02-02吴嘉伟李云州
吴嘉伟,李云州,宋 雨
(厦门大学建筑与土木工程学院,福建厦门361005)
近年来,过街人行天桥快速发展,但人行天桥跨度的增大及质量的减轻会导致结构频率变小,容易在行人或者桥下车辆的激励下发生共振引起振动过大从而影响桥上行人的舒适度[1].
我国仅在20世纪90年代编制出台了一份人行天桥规范《城市人行天桥与人行地道技术规范》(CJJ69—1995)[2],并沿用至今.该规范仅通过规定人行天桥基础自振频率不小于3 Hz的方法来避免人桥共振现象的发生,而近年国内很多新建轻柔型大跨人行天桥自振频率已很难达到该数值.因此,研究当人行天桥基频小于3 Hz 时能否达到舒适度要求是非常必要的.
国内对人体振动舒适度的研究起步较晚,到目前为止研究成果很少.20世纪30年代,杨毅[3]提出了振动的舒适性取决于振动速度的概念.随后,很多西方国家也有大量关于人体对振动舒适度感受方面的研究[4].
Goldman[5]通过研究建议将人体能感受到的振动加速度最低限值设定为0.1 m/s2.Dieckmann[6]研究认为人体的共振频率约为5 Hz.Leonard[7]通过研究表明:站在原地不动的行人对振动的主观感受要比移动的行人更加敏感.
此后,世界上发达国家也相继颁布了有关振动舒适度的规范,如德国EN03规范[8]、英国BS 5400规范[9]、日本AIJ规范[10]等等.
本文以厦门市环岛路白城空间曲线斜拉人行天桥为工程背景,基于国内外研究成果与相关规范,采用通用有限元分析(ANSYS)软件,根据实例建立有限元模型,探讨当人行天桥基频小于3 Hz时是否仍能满足舒适度要求,并提出一种行人流量限制措施以保证此类桥梁不会出现舒适度问题.
1 工程概况
该人行天桥位于厦门市环岛路,为空间曲线独塔斜拉三跨连续钢箱梁桥,主梁为轻型的封闭式钢箱梁.人行天桥平台呈马鞍形,由3段半径分别为R=12,30,12 m的圆弧组成,立面为竖曲线,其半径为R=69.19 m,实际钢箱梁为一空间曲线,桥梁展开全长为79.4 m,桥面宽度为3.75 m.桥梁左右两端各设置一个边墩,间隔两端锚固点8 m,在马鞍形中部设一斜置钢索塔.索塔与钢箱梁采用钢拉索连接,分布在两个边墩之间.桥梁立面正视图如图1所示.

图1 桥梁正视图Fig.1Front view of the bridge
2 德国EN03规范
将中国、德国以及英国等国家规范进行对比分析,结果表明德国EN03规范根据不同的人群荷载模型提供了不同的舒适度指标,适用性较强,且各项指标与其他国家相关规范相差不大,同时对人群荷载模型的定义较清楚,因此本文选择德国EN03规范对所研究的人行天桥进行舒适度验算.
舒适度验算是根据不同行人密度在满布人群荷载情况下,计算主梁各截面可能达到的最大峰值加速度.竖向与横向振动加速度的限值按表1进行判断.

表1 德国EN03规范舒适度建议值Tab.1 Suggested comfort value of German EN03 standard
德国EN03规范规定的竖向一阶振动敏感频率范围是1.25~2.30 Hz,竖向二阶振动敏感频率范围是2.5~4.6 Hz,横向振动敏感频率范围是0.5~1.2 Hz,若桥梁自振频率(基频)在此范围内则需要根据EN03规范进行舒适度验算.本文所研究的空间曲线斜拉人行天桥由于桥梁的特殊性,将振型分解为简单的竖向振动与横向振动是比较困难的,且一阶自振频率为2.048 Hz,因此无需进行横向振动加速度峰值验算,只需对竖向振动进行舒适度评价.由于该人行天桥竖向一阶自振频率处于德国EN03所规定的竖向一阶敏感范围内,竖向二阶自振频率5.666 Hz不处于敏感范围内,因此仅需对竖向一阶进行竖向振动动力响应分析.
3 竖向一阶振动及舒适度评价
3.1 竖向一阶振动行人荷载模型
基于ANSYS对桥梁进行如图2所示的建模分析,并据此进行舒适度评价.
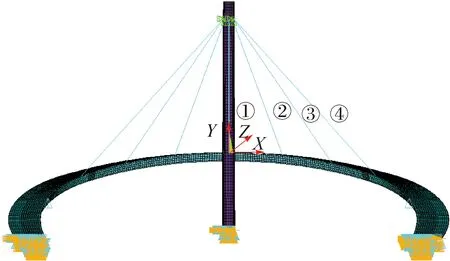
图2 有限元模型及拉索编号Fig.2Finite element model and inhaul cable number
根据德国EN03人行桥设计指南,无论是人流密度d为低密度(d<1.0 m-2)的TC1~TC3交通级别,还是为高密度(d≥1.0 m-2)的TC4~TC5交通级别,均采用同一个简谐波荷载模型,只是荷载模型中等效行人密度参数的计算方式不同,荷载模型计算公式如下[8]:
p(t)=Pcos(2πfst)n′ψ.
(1)
式中:P为单人产生的荷载幅值;fs为行人步行频率,可以假设与桥梁基频相等;n′为加载面积上的等效行人密度;ψ为折减系数;t为加载时间.
单人荷载幅值P竖向取280 N,纵向取140 N,横向取35 N,折减系数ψ的参考取值如图3[8].

图3 折减系数ψFig.3Reduction coefficient ψ
加载面积为S时等效行人密度n′参考值如下:
(2)
其中:ξ为结构的阻尼比;n为在加载面积S上的行人数量,且n=Sd.谐波荷载的加载方式根据振型来施加.
本文所研究的人行天桥主要计算参数如下:行人步行频率取竖向一阶自振频率fs=2.048 Hz,桥梁加载面积S=265.5 m2,钢结构桥梁阻尼比根据规范取ξ=0.02,折减系数根据上文曲线均取ψ=1.0,研究的竖向一阶振动单人荷载幅值P=280 N,根据德国EN03规范给定的交通等级TC1~TC5的划分,可得出TC1~TC5各交通等级情况下的p(t),如表2所示.

表2 竖向一阶振动的荷载模型Tab.2 Load model of vertical first-order vibration
3.2 竖向加速度反应分析
将表2所列的荷载模型按照TC1~TC5交通级别加载至有限元模型中计算结构的动力响应.由于本文研究的人行天桥为空间曲线桥,桥面不在同一个水平面上,但德国EN03规范所给定的荷载模型是按照加载面积来加载的,所以为了保证所加荷载均为竖直方向,采用节点荷载代替面荷载的形式加载,加载之前先通过简单小模型进行试验验证了该方法的可行性.
TC1~TC5工况下均取半跨4个关键截面作为观测点,分别是主梁跨中截面(1号拉索位置)、中跨3/8截面(2号拉索位置)、中跨1/4截面(3号拉索位置)、中跨1/8截面(4号拉索位置).动力分析时长均取40 s,分析时间步长取单个荷载周期的1/20,为0.024 414 s,以保证计算精度.由于荷载施加刚开始时对结构有冲击作用,前期约0.5 s时间内数据不准确,存在较大波动性,所以各工况结构振动加速度以稳定时读数为准.
经计算,分析时长达到20 s时振动加速度数值已很稳定,以TC1工况为例,TC1工况一阶竖向振动加速度响应曲线见图4.
将TC1~TC5工况的结果汇总成如表3所示.

图4 TC1工况中竖向一阶振动加速度曲线Fig.4Acceleration curve of vertical first-order vibration in TC1 working condition
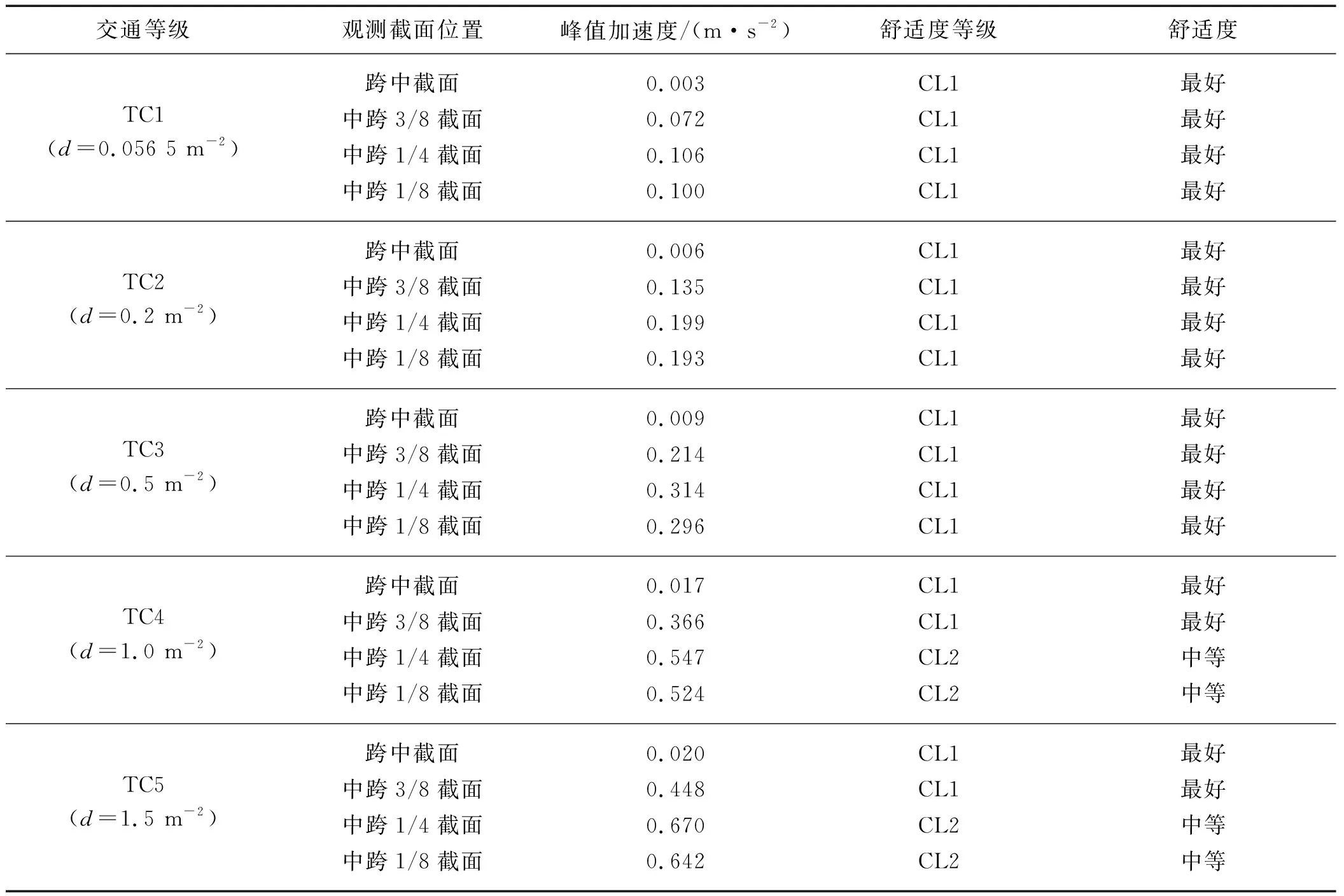
表3 竖向加速度响应汇总表
3.3 舒适度评价
从各个工况下主梁各截面的竖向加速度响应可知,最大峰值加速度均出现在中跨1/4截面,跨中截面加速度非常小,这与同振型函数方向保持一致的加载方式相吻合,且随着交通等级的增加,各观测截面的峰值加速度也随之增大.
根据德国EN03规范中对人行天桥舒适度的判别标准可知,竖向加速度峰值小于0.5 m/s2时为最好,处于0.5~1.0 m/s2之间时为中等.最终得到如表3所示各截面在TC1~TC5交通等级下对应的舒适度.
综上,本文对该空间曲线斜拉人行天桥进行舒适度评价结果为“中等”,可以满足德国EN03规范舒适度要求,行人正常行走时不会出现不适情况.
3.4 使用建议
根据计算获得的的竖向加速度响应及舒适度评价,在重交通情况下,该人行天桥的舒适度虽然能够满足要求,但不是处于“最好”状态,结合表2各交通等级对应的行人密度,在实际使用面积为265.5 m2的基础上对该人行天桥在日常使用过程中提出以下建议:
1) 当人流密度小于0.5 m-2,即交通等级为TC1~TC3时,桥上行人数量小于133,行人舒适度感受最好,行走不受限制,无需对人流量进行控制;
2) 当人流密度大于0.5 m-2且小于1.0 m-2,即交通等级为TC3~TC4,桥上行人数量控制在266以内时,正常行走已经会受到限制,大多数行人不会产生不舒适感觉,极少数敏感人群可能会产生不适感,可视情况对人流量进行控制;
3) 当人流密度处于1.0~1.5 m-2之间,即交通等级为TC4~TC5,桥上行人数量超过266时,行人十分拥挤,行走已非常困难,较多行人能够感到轻微不适,不过不会造成恐慌情况,需对人流量进行控制.
综上,根据桥梁日常使用情况及有限元分析结果,基于行人感受最佳原则,建议将交通等级控制在非常密集交通情况内,此时行人数量应控制在266以下,既能保证大流量行人过桥需求,又能保证行人感受舒适.
4 结 论
利用ANSYS软件的参数化建模功能及瞬态分析功能,基于德国EN03规范对厦门市环岛路白城人行天桥进行舒适度评价,得出了以下结论:
1) 采用德国EN03规范荷载模型对人行桥进行加载显示最大峰值加速度均出现在中跨1/4截面,且随着交通等级的加重,各观测截面的峰值加速度也随之增大.根据德国EN03规范中人行桥舒适度的判别标准,在TC1~TC5交通等级下满足对舒适度的要求.由此说明人行天桥基频于3 Hz时舒适度也能满足要求,国内CJJ69—1995规范对竖向自振频率不应小于3 Hz的规定较保守.
2) 桥上行人数量超过266时行走已非常困难,容易造成行人不适,为保证行人舒适度,建议在桥梁日常使用中将行人数量控制在266以下.
