大型结构局部非线性问题的数值子结构方法的验证与改进

2021-02-02邱栋星孙宝印

厦门大学学报（自然科学版） 2021年1期

邱栋星，汪磊，孙宝印，古泉*

(1.厦门大学建筑与土木工程学院，福建厦门361005；2.大连理工大学建设工程学部，辽宁大连116024)

近年来，随着我国经济快速增长，超大型结构的建筑越来越多.一方面，这些重大工程的投资巨大且影响深远，对结构的安全性提出了更高的要求；另一方面，近些年来，地震灾害频发，地震导致结构破坏甚至倒塌是造成经济损失与人员伤亡的重要原因之一.因此，研究超大型结构的破坏全过程和倒塌机制对于其安全性设计意义重大，针对这一问题提出高效且准确的数值计算方法非常必要.

为了深入研究结构的地震损伤和倒塌机制，对大型结构进行有限元分析时，通常需要对整体结构建立精细化数值模型[1].考虑到大型复杂结构精细化模型的单元数目以及自由度数动辄10万～100万，导致计算效率比较低.更重要的是，当某些局部关键构件进入非线性时，其结构整体刚度矩阵会改变.在常规的非线性有限元计算过程中，每一时步求解非线性方程组时都需要进行整体刚度矩阵的集成和三角分解，非常耗时，严重降低了计算效率[2].由孙宝印等[3]提出的数值子结构方法将进入非线性的局部构件从整体有限元模型中隔离出来,单独进行精细化模拟和分析，而整体模型仍然保持线弹性，能有效地提高计算效率；林纯等[4]和孙宝印等[5]基于隔离数值子结构方法对高层建筑结构进行的动力分析验证了这种方法的高效性和准确性.

然而此方法目前仍存在不足.非线性修正力项通过隔离子结构模型的静力分析得到，即仅仅考虑了静力修正，惯性力在主结构中计算而不需修正.此方法不适用于动力子结构问题；且使用不迭代算法的数值子结构方法要求计算步长很小，导致计算时间较长，计算效率不高[6-9].针对这两个问题，本研究拓展了数值子结构方法，将非线性修正力计算从子结构静力分析拓展到动力分析问题中；同时提出隔离子结构的响应预测修正方法，可显著增加计算步长，极大地提高计算效率.基于改进的数值子结构方法，对梁柱和平面连续构件进行动力分析，通过与完整结构的标准解进行对比，系统验证了此改进方法的计算精度和计算误差.

1 数值子结构方法及其改进方法

数值子结构方法将超大型结构的非线性动力问题分解为两个较简单的问题，即适度规模的主结构非精细化分析和少量非线性隔离子结构的精细化分析问题.主结构采用线弹性非精细化模型，计算规模适度；在整个计算过程中刚度保持不变，只需要进行一次刚度矩阵集成和三角分解，效率很高.少量非线性区域采用精细化隔离子结构模型，规模较小，计算效率高.主结构与子结构之间的的边界满足位移边界协调和力平衡条件.本研究中主、子结构之间的信息传递使用客户机/服务器(C/S)集成技术，可实现基于网络通道的并行分布式计算[10].以下简要介绍数值子结构方法的计算公式.

基于有限元的整体结构运动方程为[11]：

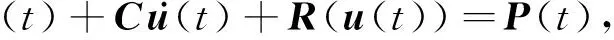
(1)

1.1 基于子结构静力分析法的非线性修正力

将式(1)按Newmark-β法对时间t进行离散，则

(2)

在式(2)的左右两边同时加上Kun+1项并整理，可得

(3)

(4)

(5)

(6)

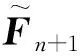
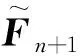
如图1所示，ub为子结构边界上的节点位移.假设子结构边界上节点位移是连续的，ub可根据式(7)插值得到：

ub=NuNL.

(7)

其中：N为形函数，用于插值得到子结构连续边界上的节点位移；uNL(见图1)为线弹性主结构隔离区域的节点位移.在每一个小的时步中，式(7)也可以被写成以下增量形式：

δub=NδuNL.

(8)

根据虚功原理，主结构隔离系统与子结构系统的虚功是相等的，即

(9)

(10)

将式(8)带入到式(10)中可得

RNL=NTRsub,b.

(11)

由此可得隔离区域的非线性修正力在子结构进行精细化模拟时的计算公式：

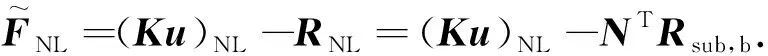
(12)

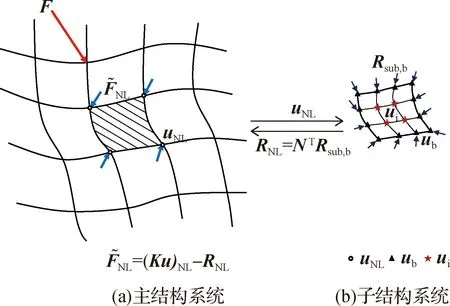
图1 精细化子结构模型的非线性修正力计算方法Fig.1Calculation method of nonlinear correction force for refined substructure model

以上介绍的是子结构模型进行静力分析时的非线性修正力的计算，其只考虑位移边界u，而对子结构的惯性力项并未考虑，无法准确模拟子结构的动力问题.

因此，以下介绍子结构动力分析时的非线性修正力的公式推导.

1.2 基于子结构动力分析法的非线性修正力

动力分析时把运动方程对时间t进行离散，每一时步都满足以下方程：

(13)

(14)

(15)

其中

(16)

而等效动力刚度和改进的非线性修正力分别为：

(17)

(18)

(19)

根据虚功原理，主结构隔离系统与子结构系统的虚功是相等的，即

[RNL+(MNLüNL)]TδuNL=[Rsub+

(Msub,büsub,b)]T,[Rsub,i+

(20)

其中：MNL为主结构隔离区域的节点质量，Msub为子结构系统的节点质量，Msub,b、Msub,i分别为子结构系统的边界节点和内部节点质量.由于内部节点不受外力作用，其内部节点的结构抗力Rsub,i与惯性力Msub,iüsub,i的和始终为0.因此，同理可得

RNL+(MNLüNL)=NT[Rsub,b+(Msub,büsub,b)],

(21)

将式(21)代入(18)，可得子结构动力分析时隔离区域的非线性修正力的计算公式：

NT(Msub,büsub,b)].

(22)

1.3 算法流程简介

本研究分别采用不迭代与迭代算法对隔离数值子结构中的动力问题进行分析.其中不迭代算法的流程可分为以下几个步骤：

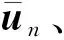
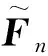
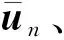
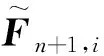
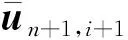
1.4 预测改进的隔离数值子结构方法

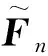
(23)

预测改进的隔离数值子结构方法可分为以下几个步骤：

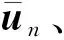
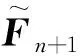
2 隔离数值子结构方法的验证(梁柱单元)

本节采用一根长度为6 m的竖向悬臂梁对隔离数值子结构方法进行验证.梁柱模型如图2所示.图2(a)为主结构模型，其包含2个梁柱单元，3个节点，节点1采用固定约束.梁柱截面为复合截面，抗拉压以及抗弯材料均选用应力σ-应变ε如图3所示的双线性本构模型，其中，抗拉压刚度和抗弯刚度一样，其弹性模量E均为5.74×106MPa，屈服点的应力fy为1.47×104MPa，b为刚度比，此处取0.6.

在计算过程中，为了简化问题，选取图2(a)中的①单元为隔离单元(线弹性的主结构模型，见图2(a)右侧)，图2(b)为精细化弹塑性子结构模型.在主结构的3号节点分别施加静力、动力荷载，并使用两种隔离数值子结构方法对该模型进行响应分析.

图2 梁柱单元隔离数值子结构方法的模型示意图Fig.2Schematic diagram of the model for numerical substructures method of beam-column unit

图3 双线性本构模型Fig.3Bilinear constitutive model

2.1 梁柱单元静力荷载下弹塑性验证

图4 梁柱单元标准模型Fig.4Standard model of beam-column unit

图6 梁柱单元动力荷载下节点4的位移响应Fig.6Displacement response of node 4 under dynamic load of beam-column unit

图5为梁柱单元的4号节点在静力荷载作用下水平位移.由图可知，采用迭代与不迭代算法的隔离数值子结构方法的计算结果与标准模型的解保持一致；当荷载加载完成时(t=1.0 s)，单元①已进入塑性阶段，标准模型的4号节点的水平位移为3.879 35 cm，而采用迭代隔离数值子结构方法的计算结果也为3.879 35 cm，与标准解相同；采用不迭代隔离数值子结构方法的计算结果为3.866 88 cm，与标准解的相对误差为0.3%.

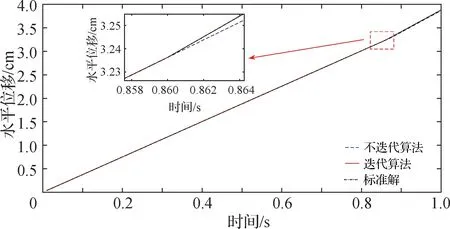
图5 梁柱单元静力荷载下节点4的位移响应Fig.5Displacement response of node 4 under static load of beam-column element

2.2 梁柱单元动力荷载下弹塑性验证

当对模型进行动力响应分析时，由于需要考虑惯性项，所以对模型的精细化模拟需要对质量进行重新分配.本节中所采取的质量矩阵为集中质量矩阵，质量分配的规则如图2和图4所示.节点4受到单点激励，输入的波形选用的是1989年美国洛马-普雷塔的Loma Prieta地震波，放大倍数为300倍.

如图6所示，对该模型进行动力分析时，静力迭代算法的非线性修正力计算是基于子结构静力分析得到的，其计算结果与标准解的误差为5%.将子结构从静力分析拓展至动力分析后，迭代的隔离数值子结构方法的计算结果与标准解保持一致；不迭代算法的计算步长为10-3s时，计算过程中的位移发散，计算无法完成；缩小计算时间步长后，不迭代算法与标准解在弹性阶段吻合较好，误差保持在1%以内，但是当单元1进入塑性阶段，计算结果并不理想，误差达到35%，此时，不迭代算法的计算时间步长为10-4s，计算成本较大.为了加快不迭代算法的计算效率及计算精度，本文提出的预测改进的不迭代隔离数值子结构方法将时间步长增大为10-3s，相比于普通的不迭代算法的计算效率提高了10倍，且计算结果与标准解的误差仅为0.81%，极大地提高了不迭代算法在模拟结构动力响应分析时的计算精度.

3 隔离数值子结构方法的验证(平面四节点单元)

本节中的模型如图7所示，图7(a)为完全弹性的主结构模型，取单元①作为隔离数值子结构(如图7(b))，并将其精细化，如图7(c).主结构共有8个节点，3个单元，每个节点2个自由度.结构采用四节点单元，每个单元大小为3 m×3 m. 1和2节点为固定端.本算例为平面应变问题，单元厚度取0.1 m，分别使用两种隔离数值子结构方法对模型在静力以及动力荷载作用下的结构响应进行分析.

图7 四节点单元隔离数值子结构方法的模型示意图Fig.7Schematic diagram of the model for numerical substructures method of four-node unit

3.1 平面四节点单元静力荷载下的弹塑性验证

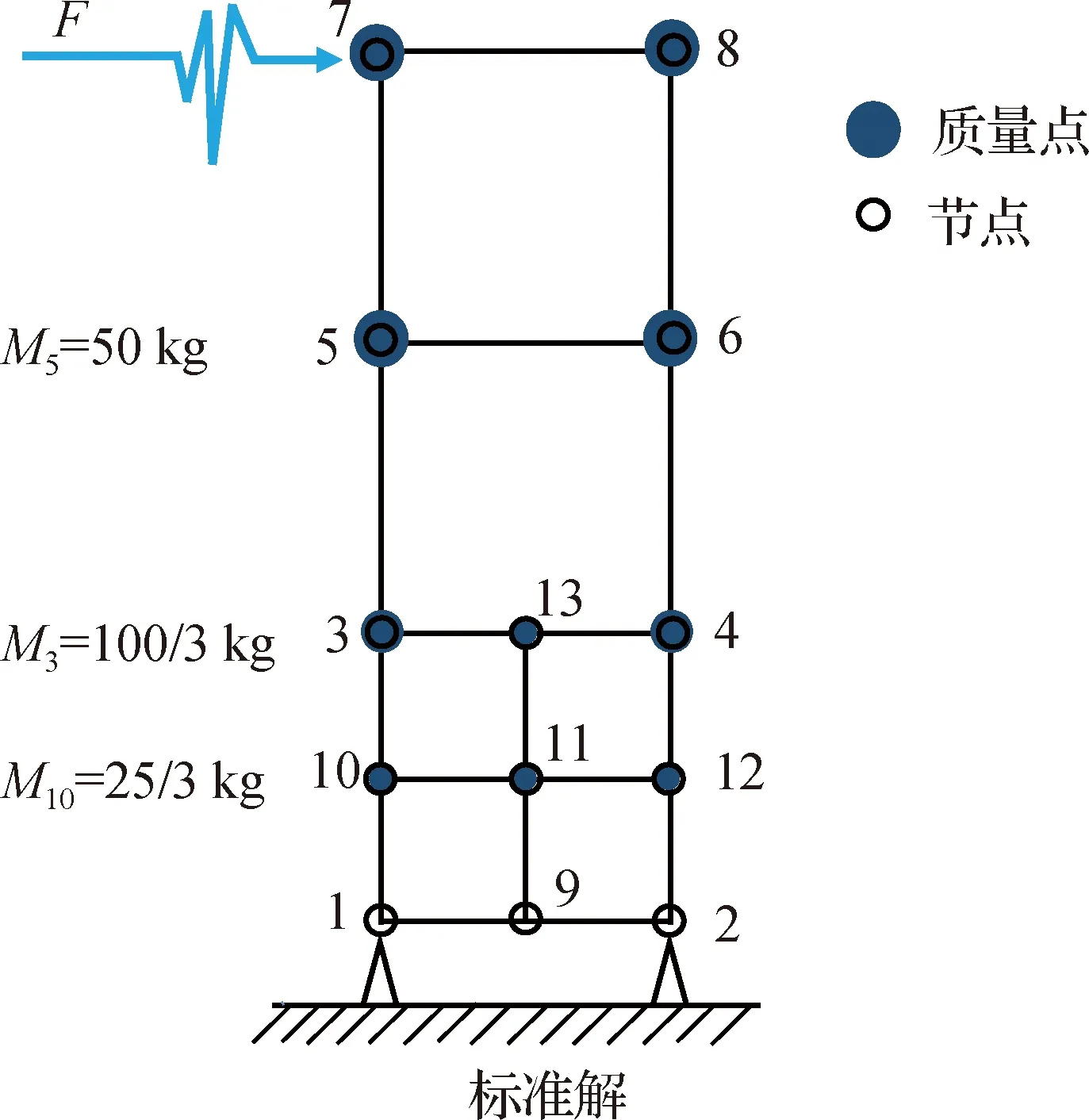
图8 四节点单元隔离数值子结构方法的标准模型示意图Fig.8Schematic diagram of the standard model for numerical substructure method of four-node unit

为了验证两种隔离数值子结构方法在平面四节点单元上的正确性，本节中参照隔离数值子结构方法的模型网格尺寸进行完整结构的建模(见图8)，并将其作为标准模型.由于在标准模型的求解过程中需要使节点9、10、12、13满足一定的位移约束条件，即在求解等效动力平衡方程时需增加一个约束矩阵T，则动力方程为：

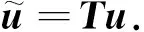
约束矩阵T可由节点9、10、12、13与相邻节点的位置关系确定.例如在本节中，3、4、13号节点的位移满足以下关系：

图9 平面四节点单元静力荷载下节点8的位移响应Fig.9Displacement response of node 8 under static load of planar four-node element

由图9可知，当静力荷载加载完成时(即t=1.0 s)，标准模型的8号节点水平位移的标准解为55.064 4 cm，而采用迭代的隔离数值子结构方法的计算结果为55.064 4 cm，与标准解相同；而不迭代算法的计算结果为53.649 7 cm，与标准解的相对误差为2.6%.

3.2 平面四节点单元动力荷载下的弹塑性验证

在动力荷载下精细化的子结构模型需要考虑惯性项，需要对节点质量进行重新分配，其分配规则如图7和8所示.在标准模型中，5、6、7、8号节点的质量均为50 kg，3和4号节点的质量均为100/3 kg，10、11、12、13号节点的质量均为25/3 kg.7号节点受到单点激励，输入的波形选用的是1989年美国洛马-普雷塔的Loma Prieta地震波，放大倍数为1 600倍.

如图10所示，在动力荷载作用下，非线性修正力的计算是基于子结构静力分析得到的静力迭代算法，其计算结果与标准解的相对误差为7.61%.将子结构从静力分析拓展至动力分析后，采用迭代的隔离数值子结构方法的计算结果与标准解的计算结果基本保持一致.当t=9.88 s时，标准模型中8号节点的水平位移为-40.593 4 cm，而采用迭代算法时，其水平位移为-40.625 3 cm，相对误差为0.08%.采用普通的不迭代隔离数值子结构方法，当计算步长为10-3s时，计算过程中的位移发散，计算无法完成；当缩小计算步长至10-5s，其计算结果为-40.731 8 cm，与标准解的相对误差为0.34%；使用预测改进的不迭代隔离数值子结构方法后，其计算步长可增大为10-3s，计算结果为-40.712 3 cm，计算效率提升了100倍，而相对误差仅为0.29%.