用新陈代谢极限学习机实现电池健康状态估算*

2021-02-02王惠民李熠婧潘海鸿

汽车工程 2021年1期

陈琳，王惠民，李熠婧，张沫，黄江，潘海鸿

（1.广西大学机械工程学院，南宁 530004；2.广西电化学能源材料重点实验室（广西大学可再生能源材料协同创新中心），南宁 530004）

前言

锂离子电池因具有能量密度大和循环寿命长等优势作为主要储能元件被广泛应用于电动汽车和可再生能源系统等各个工业领域［1-3］。由于锂离子电池的性能状态直接影响到整个系统的稳定性和可靠性，对其健康状态（state of health，SOH）进行估算十分必要。SOH主要反映电池当前性能相对于其初始状态的变化，它决定电池的维护和更换时间，可为电池提供决策性保护［3-4］。因此，准确估算SOH 对于保障储能系统性能、降低成本和提高安全性等方面具有重要意义［5］。

近年来国内外学者已在SOH 估算领域开展了大量研究，主要方法可大致分为3 类：机理分析法［6-7］、基于滤波法［1，8］和数据驱动法［9-14］。其中，数据驱动方法因其无需进行深入的机理研究，仅靠挖掘历史数据的潜在规律就可以描述复杂的电池退化过程而受到广泛关注［1］。这类方法主要包括支持向量机（support vector machine，SVM）［9-10］、神经网络［11-12］和高斯过程回归（gauss progress regression，GPR）［13-14］等。文献［9］中在考虑多负载集合和容量测试耦合性的情况下，将SVM 用于电池容量变化的回归预测来实现锂离子电池的SOH 估算。文献［10］中引入粒子群优化算法对SVM 的超参数进行优化，减少使用SVM 估算SOH 时带来的泛化误差。文献［11］中使用电池的动态历史数据分布训练其所构建的反向传播神经网络框架，结果表明该框架可用于多工况下的电池SOH 估算。文献［13］中提出了一种利用多电池数据的多输出GPR 模型，该模型充分利用GPR 的超参数自适应调节的优点，显著提高SOH 预测性能。这些数据驱动方法在非线性非高斯的SOH 估计中具有良好的适应性，并且在输入充足历史数据的情况下可以达到很高的精度［1，5，12］。但在输入数据量较少的情况下，数据驱动算法的泛化性能会下降［5］，影响估算效果。因此，如何在小数据样本情况下对SOH 进行准确估算成为数据驱动方法的研究难点。

极限学习机（extreme learning machine，ELM）具有结构简单和易于调整参数等优点［15］，已被应用在其他领域的回归预测案例中。与SVM 和BPNN 等相比，其训练速度更快且不易陷入局部最优，泛化能力十分优秀。因此，基于在线提取的退化特征和容量退化量，引入ELM 来利用其泛化性优势构建一种描述电池复杂退化过程的退化状态模型，并结合新陈代谢机制对小数据样本情况下的电池SOH 进行估算。此外，采用正极材料分别为钴酸锂和镍钴铝三元材料的电池在动态工况下的测试数据对所提方法的SOH估算效果进行验证。

1 基本方法

1.1 基于退化特征提取的退化状态模型构建

电池的退化是典型的非线性时变过程，每个循环的退化量与之前循环的参数变化都密切相关，而这种退化关系的详细电化学机理十分复杂，很难通过具体的数学公式进行量化。为此提出构建一种以容量退化为状态变量的电池退化状态模型，将相邻循环之间容量退化量的关联性抽象地表示为

式中：ΔCk为第k 个循环的容量退化量；f（·）为根据第k-1 个循环的容量退化量ΔCk-1建立的描述电池退化机理的函数。

当电池容量退化发生较大变化时，式（1）中的模型可能无法有效地跟踪电池容量的退化，为此提出引入其他退化特征对该公式进行修正。因此，根据电池的放电电流和电压数据建立电池的1 阶RC 模型，使用递推最小二乘算法实时辨识出电池的欧姆内阻R0和极化内阻R1，并将这两种内阻用于表征电池退化过程［16］，结合两种内阻和容量退化量构建老化模型。内阻辨识的主要步骤如下。

建立电池的1 阶RC 模型（图1）。图中：UOC表示电池的开路电压；R1和C1表示电池内部的极化内阻和极化电容，分别代表电池内部电化学反应的极化特性和扩散效应；R0是电池的欧姆内阻，主要包括电池隔膜电阻和其他接触电阻。

图1 电池的1阶RC模型

由Kirchhoff 定律可以得到1 阶RC 模型的电路表达式：

式中：Ut为电池端电压；U1为RC 网络两端的电压；IL为负载电流。

将式（3）代入式（2）并进行z 变换，得到式（2）的离散表达式：

式中：k为采样时刻；Uoc，k、Ut，k和IL，k分别为电池在k时刻的开路电压、端电压和负载电流；Ts为采样周期。

式（4）中的参数Ut和IL都可以通过仪器直接测量获取，因此矩阵Φk完全已知。之后可通过式（5）对矩阵Θk进行递推求解：

式中：λ 为遗忘因子，本文中取值0.95；Pk和Kk分别为k 时刻的协方差矩阵和增益矩阵。根据式（5）计算得到Θk之后，即可通过式（4）求解出R0、R1、C1的值。

文献［1］中指出，电动汽车动力电池的实际工作荷电状态（SOC）区间主要为［25%，95%］；前期研究［17］中发现，当电池在其SOC 处于［30%，80%］区间内充放电时，实时辨识出的R0和R1基本保持不变。因此，选择电池在每个循环SOC 的［30%，80%］区间内的平均欧姆内阻和平均极化内阻来代表实际应用环境中的真实电池内阻。平均欧姆内阻和平均极化内阻的计算方法见式（6）和式（7）。

然而，温度变化对电池内阻存在明显影响，不同温度下所辨识出内阻的数值差异较大，将其作为特征提取会增加算法复杂度和计算处理过程，影响模型的估算效率和精度。故选择将欧姆内阻和极化内阻的增量作为电池的退化特征，计算方式见式（8）和式（9）。

式中g（·）为根据第k-1个循环的容量退化量ΔCk-1和退化特征ΔR0k-1、ΔR1k-1建立的描述电池退化机理的函数。

1.2 ELM基本算法原理

由于电池内部电化学反应过程十分复杂，导致式（10）所给出的退化状态模型很难得到准确的解析表达式，为此提出使用ELM 算法对退化状态模型进行拟合。ELM是一种对输入权值和隐含层节点偏差进行随机赋值的单隐层前馈神经网络［15］，其学习效率高且泛化性能好。算法基本过程如下。

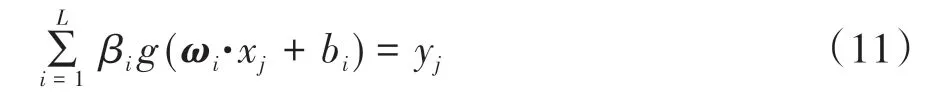
式中：j=1，2，…，N；ωi=[ωi1，ωi2，…，ωin]T为连接第i个隐含层节点和输入节点的输入权值；bi为第i 个隐含层节点的偏差；βi为连接第i 个隐含层节点和输出节点的输出权值。

式（11）可以被简写成线性方程组：

其中：

式中ωi和bi为随机赋值。只需再求出βi的值即可完成ELM 训练。βi可通过求式（12）的最小二乘解来确定：

式中H+是H的Moore⁃Penrose广义逆矩阵。

1.3 基于新陈代谢ELM的电池SOH估算架构

采用新陈代谢ELM 进行锂离子电池SOH 估算的主要框架如图2 所示，主要包括离线构建退化状态模型和新陈代谢ELM在线估算SOH。

1.3.1 离线构建电池退化状态模型

采用电池全生命周期的测试数据获取每次老化循环中的容量退化量序列｛ΔC｝、欧姆内阻增量序列｛ΔR0｝和极化内阻增量序列｛ΔR1｝。将｛ΔC｝、｛ΔR0｝和｛ΔR1｝作为输入训练数据，输入数据｛ΔC｝中每个循环对应的下一循环容量退化量作为目标输出数据，根据式（11）～式（14）计算ELM 的输出权值βi，完成基于ELM 的电池退化状态模型的训练，即确定式（10）中g（·）的具体形式，记为gELM（·）。

图2 基于新陈代谢ELM的电池SOH估算框架

1.3.2 新陈代谢ELM在线估算SOH

实际工况下的电池状态呈现强时变特性，最新的数据才能充分反映电池退化的最新趋势和特点。因此，提出利用最新数据更新所构建的退化状态模型对电池SOH进行新陈代谢估算。具体步骤如下。

（1）假设已知历史数据的老化循环为第k-i到第k-1个循环（k>i），在线采集这i个循环的历史容量退化数据序列｛ΔCk-i→k-1｝，通过动态工况下实时采集的数据在线建立电池的1 阶RC 模型并辨识得到这些循环的欧姆内阻增量序列｛ΔR0k-i→k-1｝和极化内阻增量序列｛ΔR1k-i→k-1｝，将其作为退化特征。

其中：

（2）将待估算电池的｛ΔCk-i→k-1｝、｛ΔR0k-i→k-1｝和｛ΔR1k-i→k-1｝输入1.3.1 节中所构建的电池退化状态模型gELM（·），模型输出待估算电池的容量退化量估算值序列该步骤可以简单描述为

（3）根据式（16）计算第k个循环的SOH估算值：

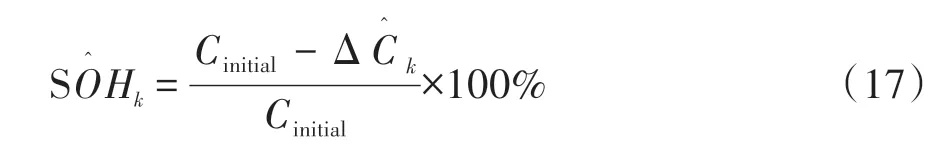
式中Cinitial为待估算电池的初始容量。

将式（18）构建的新输入序列输入电池退化状态模型gELM（·），即返回步骤（2）；不断循环步骤（2）～步骤（4）来更新估算，直至容量退化量估算值达到设定的截止阈值（电池额定容量的20%左右），停止估算。

2 实验设计

2.1 实验平台

实验平台由高低温实验箱GDW-100L、可编程直流电源ITECH IT6523D、电子负载仪ITECH IT8511、上位计算机和锂离子电池组成（图3）。其中高低温实验箱GDW-100L可实时记录实验过程中的环境温度；可编程直流电源ITECH IT6523D 和电子负载仪ITECH IT8511 用于对锂离子电池进行充放电测试，以1 Hz 频率实时采集电池在充放电过程中的电流、电压和累积充放电容量3 种数据；上位计算机用于充放电工况控制和数据储存。受测电池为商用动力锂离子电池：正极为镍钴铝三元材料（LiNCA）的松下NCR18650B电池1节（编号P01）；正极为钴酸锂（LCO）的三星ICR18650-26F 电池2 节（分别编号S17、S30）。具体型号和参数如表1所示。

图3 实验设备及其连接示意图

表1 受测电池的主要参数

2.2 实验流程

电池的实验测试主要由特性测试和老化循环测试组成（图4），电池在每次测试前都以标准恒流-恒压（constant current and constant voltage，CC-CV）充电方式充满。

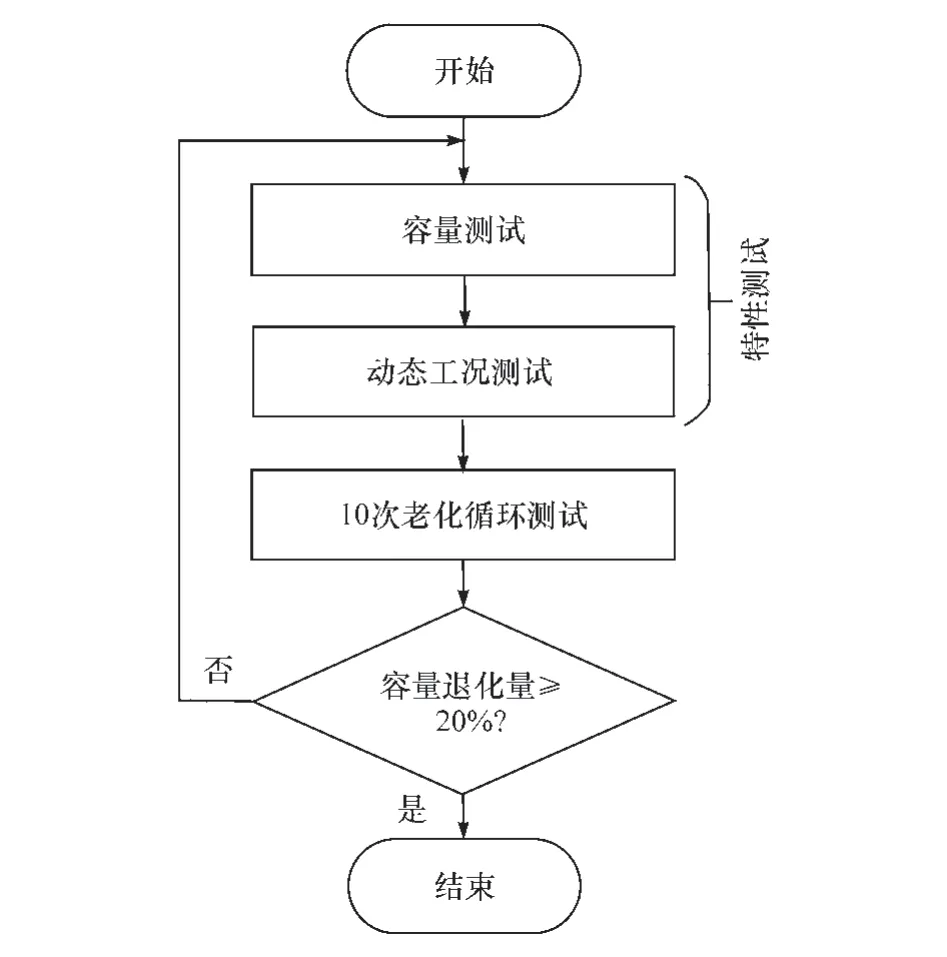
图4 老化实验流程图

（1）电池特性测试：包括一次容量测试和一次动态工况测试。①容量测试：将电池用标准CC-CV 充电法充满，之后以0.2C 倍率进行恒流放电，直至电压下降至放电截止电压。②动态工况测试：使用特定动态工况对电池进行循环放电直至电池的电压降至放电截止电压。其中P01 的动态工况测试所使用工况为25 ℃下的UDDS（urban dynamometer driving schedule）工况，S17和S30的动态工况测试分别为25和35 ℃下的NEDC（new european driving cycle）工况。特性测试不同有利于研究不同种类电池在不同工况激励下所反映出的老化特性。

（2）老化循环测试：电池老化测试则是将电池以标准CC-CV 充电法满充后，以特定老化循环工况对电池进行循环放电直至电压降至放电截止电压，该充放电步骤重复10 次。由于高温、大倍率、100%放电深度、间隔放电等要素有利于加快电池老化［18］，为加速电池老化过程，早期进行的S30 老化实验在35 ℃下使用较大倍率的脉冲电流［19］作为老化循环测试工况；后续考虑到实际环境中电池放电工况并非脉冲放电能够代替，故在S17和P01的老化循环测试中加入了UDDS工况，并提高实验温度至45 ℃，在进一步加速电池老化的同时充分体现动态工况对电池老化的影响。不同的老化循环测试有利于探究两种电池在不同动态工况下进行老化循环产生的老化差异。3节电池的实验流程对比如表2所示。

表2 受测电池的实验流程对比

重复进行电池特性测试和老化循环测试直至电池的容量退化量达到初始容量的20%。所有实验步骤均在高低温实验箱内进行，并用上位计算机实时记录。

3 实验结果与分析

3.1 退化特征与电池性能退化

根据老化实验所得容量数据，不同电池的容量随着充放电循环周期的增加都呈现出非线性下降趋势（图5）。对于正极材料为LiNCA 的电池P01，其初始容量较高，容量退化速率在整个老化过程中一直保持相对稳定，退化轨迹的斜率基本保持不变；而对于正极材料为LCO 的两节电池S17和S30，它们的退化过程则存在更多容量波动，其中S30 在退化后期表现出明显的加速退化趋势。不同电池在退化过程中表现出的不同特性为SOH 估算带来一定困难，因此寻找有效的退化特征来反映不同电池的退化特性十分必要。

按照1.1 节中递推最小二乘算法辨识电池的欧姆内阻和极化内阻。以S30 为例，其辨识出的欧姆内阻在不同充放电循环中的变化曲线如图6所示。

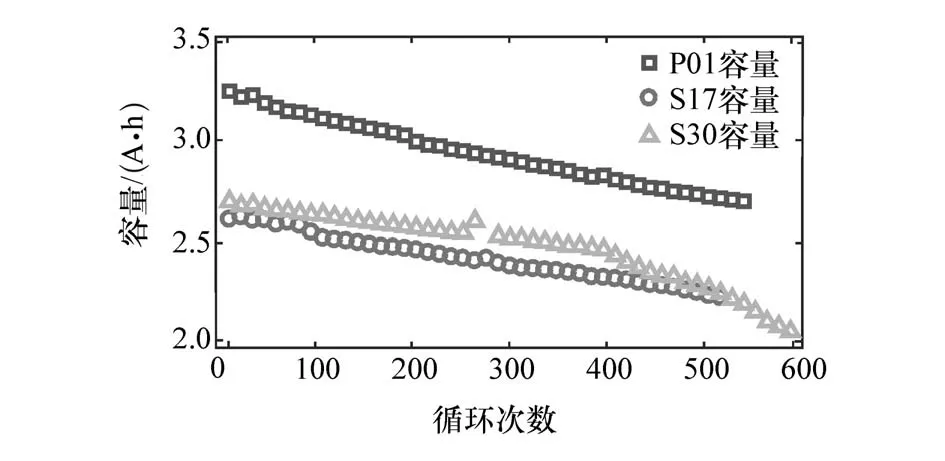
图5 P01、S17和S30的容量退化图

图6 S30辨识得到的欧姆内阻随充放电循环变化曲线

随着电池充放电循环周数的增加，电池老化程度加深，辨识得到的欧姆内阻逐渐变大，表明欧姆内阻可反映电池的老化状态。此外，在电池的单次放电过程中，当SOC 处于30%～80%区间内时，其欧姆内阻整体变化趋势相对平稳，将该区间内欧姆内阻平均值作为当前循环的标准欧姆内阻可有效减少随机误差和异常值的影响。极化内阻的变化趋势与欧姆内阻类似，此处不再赘述。根据所得内阻求其增量构建退化特征，分析其与容量退化量之间的相关程度。图7 给出P01、S17 和S30 电池的内阻增量与容量退化量的关系。

图7 中3 节电池的两种内阻增量（ΔR0和ΔR1）都和其容量退化量ΔC 存在明显正相关。但松下和三星两种电池的ΔC随两种内阻增量变化的趋势不同：正极为LiNCA 三元材料的P01 的ΔC 随ΔR0和ΔR1变化的趋势较为相似；而正极材料为LCO 的S17/S30，其ΔC 与两种内阻增量的线性关系更明显且变化趋势不同（图7（b）和图7（c））。其内阻增量变化由于测试温度不同而有所差异，在容量退化量达到0.4 A·h 时，25 ℃下测试的S43 内阻增量略大于35 ℃下测试的S30 内阻增量，这是因为温度会影响锂离子迁移速度，且锂离子脱出速度和嵌入速度的变化也不同［20］。虽然不同温度对内阻增量有一定影响，但电池容量退化量和内阻增量仍然存在近似线性关系。

使用皮尔逊（Pearson）积矩相关系数rp和斯皮尔曼（Spearman）等级相关系数rs来定量地评判退化特征对容量退化量的影响程度。rp是量化两个变量之间线性相关程度的参数标准，rs则是用来度量两个变量之间单调相关性的指标，按式（19）和式（20）计算。两者的取值范围都在［-1，1］之间，绝对值越接近1说明变量间相关性越强。

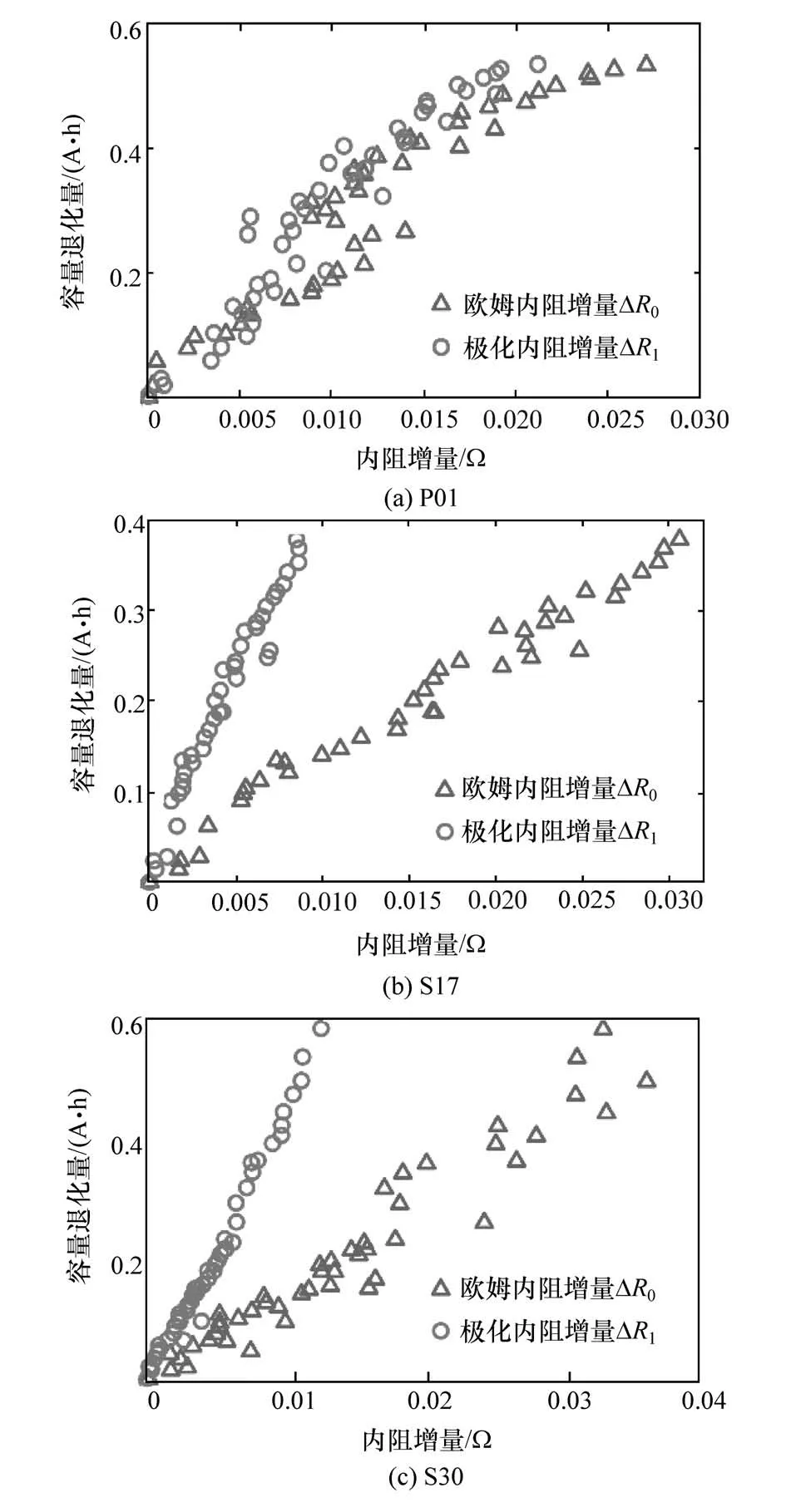
图7 不同电池的内阻增量与容量退化量的关系

式中X和Y为待分析变量序列。

分别将3 节电池的内阻增量ΔR0和ΔR1代入X，容量退化量代入Y，计算得到相关系数值，见表3。

表3 退化特征与容量退化量相关性分析结果

3 节电池的ΔR0和ΔR1与容量退化量的rp和rs都大于0.94，表明以电池内阻增加量构建的表征电池退化的退化特征和电池容量退化量间具有良好的线性关系。以在线辨识得到的锂离子电池内阻增量作为退化特征描述电池性能退化状态，用两者之间的近似线性关系修正容量退化量构建的电池退化状态模型，最终用于估算电池SOH是合理的。

3.2 SOH估算结果分析

将基于新陈代谢ELM 的电池SOH 估算框架用于不同工况和温度下的电池SOH 估算，并对估算精度进行评估。测试软件环境为MATLAB R2017a，ELM 的隐含层节点数L=30，激励函数选用Sigmoid函数。

在离线构建状态模型的参考电池和待估算电池型号及材料不同的情况下对新陈代谢SOH 估算框架进行有效性验证：使用LiNCA 电池P01 离线构建电池退化状态模型，再用材料和测试工况都不同的LCO 电池S17、S30 分别进行在线SOH 估算验证。基于ELM 的电池退化状态模型对P01全生命周期数据中提取退化特征和容量退化数据离线训练的结果如图8所示。

图8 电池退化状态模型离线训练结果

所构建的退化状态模型都能够随着P01 老化过程中的容量退化量变化输出准确的容量退化量估算值，估算误差不超过0.03 A·h，说明离线训练得到的退化状态模型能够准确描述容量退化量与退化特征之间的关系，估算结果表现出良好的跟踪性。

根据1.3 节中新陈代谢ELM 估算SOH 流程，用P01 离线训练的退化状态模型对S17 和S30 在线SOH 估算。设置S17 和S30 已知的历史数据点个数i=4，SOH 估算起始循环数k=5，估算结果如图9所示。

图9 基于新陈代谢ELM的SOH估算结果

基于P01数据离线构建的新陈代谢ELM 估算的两节电池（S17 和S30）SOH 与真实SOH 的退化轨迹都有较高的重合度。其中S17（图9（a））的真实SOH退化轨迹除老化初始阶段外相对平缓，因而估算误差最大值出现在退化初期，后续SOH 估算误差大致呈波动收敛趋势；S30（图9（b））的真实SOH 在退化中期阶段出现一次明显的波动，这是由于老化实验暂停休息期间电池容量出现暂时回升，导致该波动点对应的SOH 估算误差达到极大值，之后随着老化实验的继续进行，其真实SOH 变化轨迹逐渐趋于平缓，SOH 估算值亦能很好地跟踪真实轨迹。S30 在退化中后期出现了明显的加速退化现象，SOH 退化速率明显加快，SOH估算误差相较老化前期稍大，但其均未超过1%。表明不同工况下两节电池的真实SOH 轨迹的退化过程中出现的任何波动，新陈代谢ELM都能准确跟随其变化趋势。

为进一步验证本文所提出的电池SOH 估算框架的有效性，将未引入退化状态模型和新陈代谢机制的传统ELM 算法［19］用于SOH 对比估算：将P01 的退化特征序列｛ΔR0｝和｛ΔR1｝作为输入数据、容量退化量序列｛ΔC｝作为目标输出训练传统ELM，之后分别将S17 和S30 的退化特征序列输入训练完成的传统ELM 估算其SOH。传统ELM 参数设置与新陈代谢ELM 完全一致（隐含层节点数L=30，激励函数为Sigmoid），估算结果如图10所示。

图10 基于传统ELM的SOH估算结果

由图可见，传统ELM 的估算SOH 与真实SOH 的整体变化趋势虽然在一定程度上比较相近，但估算值与真实值在电池退化中后期逐渐出现较大偏差。用最大绝对误差、平均绝对误差和均方根误差来量化评估新陈代谢ELM 与传统ELM 两种算法对2 节电池的SOH估算精度，结果见表4。

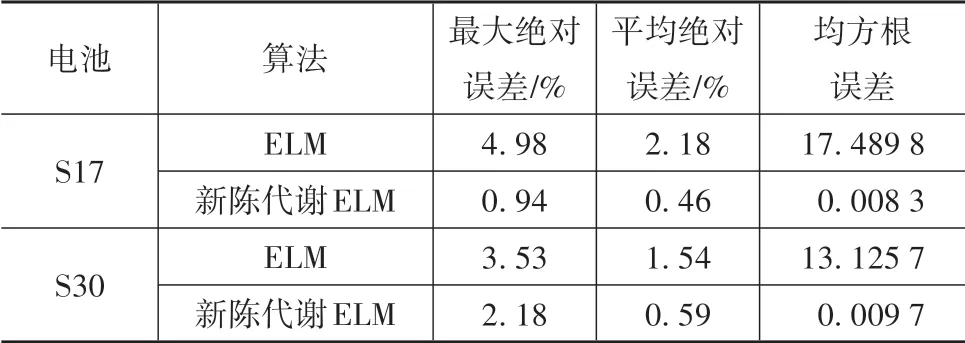
表4 SOH估算精度评估

由表可见，新陈代谢ELM 估算2 节电池SOH 的全局最大绝对误差不超过2.18%，平均绝对误差不超过0.6%且最大均方根误差仅为0.009 7，说明新陈代谢ELM 的SOH 估算结果不仅很接近真实值而且其分布的离散程度也很低。新陈代谢ELM 的各项误差指标都远小于传统ELM 算法，表明电池退化状态模型的构建和新陈代谢机制的引入对不同类型电池的SOH 估算精度提升明显，验证了所提出SOH估算方法相较于传统ELM方法的优越性。

上述结果表明，基于所提取退化特征构建的ELM电池退化状态模型能够准确描述电池退化特性和规律，结合新陈代谢机制构建的电池SOH 估算框架可在少数据样本的情况下实现对不同工况和不同材料的电池SOH 准确估算，具有良好的精度和泛化性。