两点一线最短距离的教学改进策略

文/广州市海珠外国语实验中学 王远帆

对于初中阶段的几何学习，学生需要有一个从视角直观到逻辑推理的过程。教师在教学尤其是在低年级教学中，应让学生对几何的图形的规律先从视觉上进行感知，再从数量与位置进行逻辑推理的阐述，而且讲解步骤的分解策略也显得尤其重要。

一、场景呈现

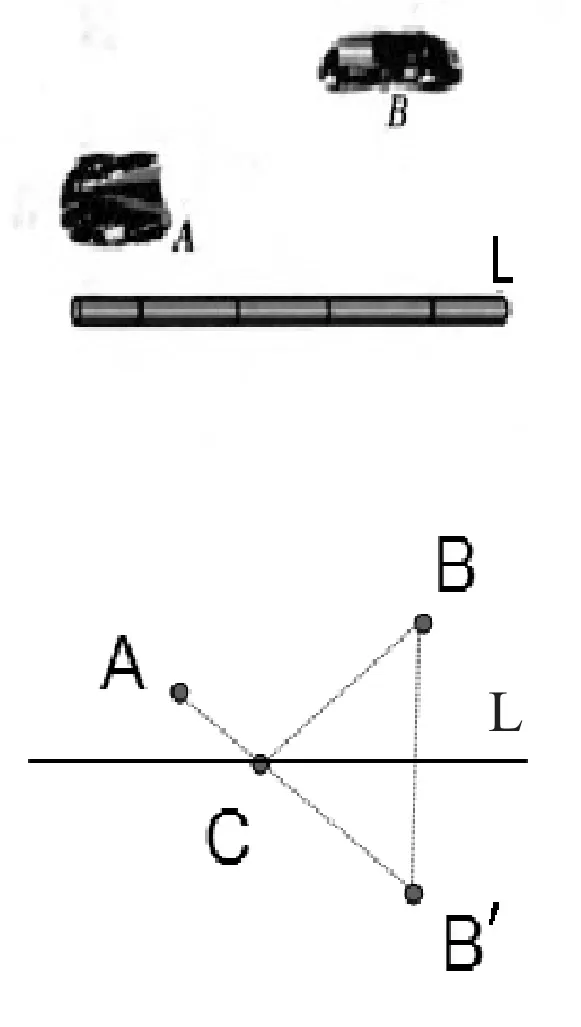
人教版八年级上册第十二章《轴对称》第二节“作轴对称图形”中有一个探究问题，问题如下：要在燃气管道L 上修建一个泵站，分别向A、B 两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？

此问题可以抽象为求两点一线、距离最短问题，如左下图所示，此问题解决的步骤：1. 求一点关于直线的对称点B'；2.连接点B'和点A，与直线L 所交的点C 即为所求点。

对于课本的推理过程，教师在没做任何铺垫的情况下，班里有超过一半的学生无法理解，其中60%的学生在教师的演绎过程中能够听明白，但是若自己动手证明或更换背景，部分学生则表示不知如何下手，这一点在课后的小测反馈中体现明显。

二、改进策略

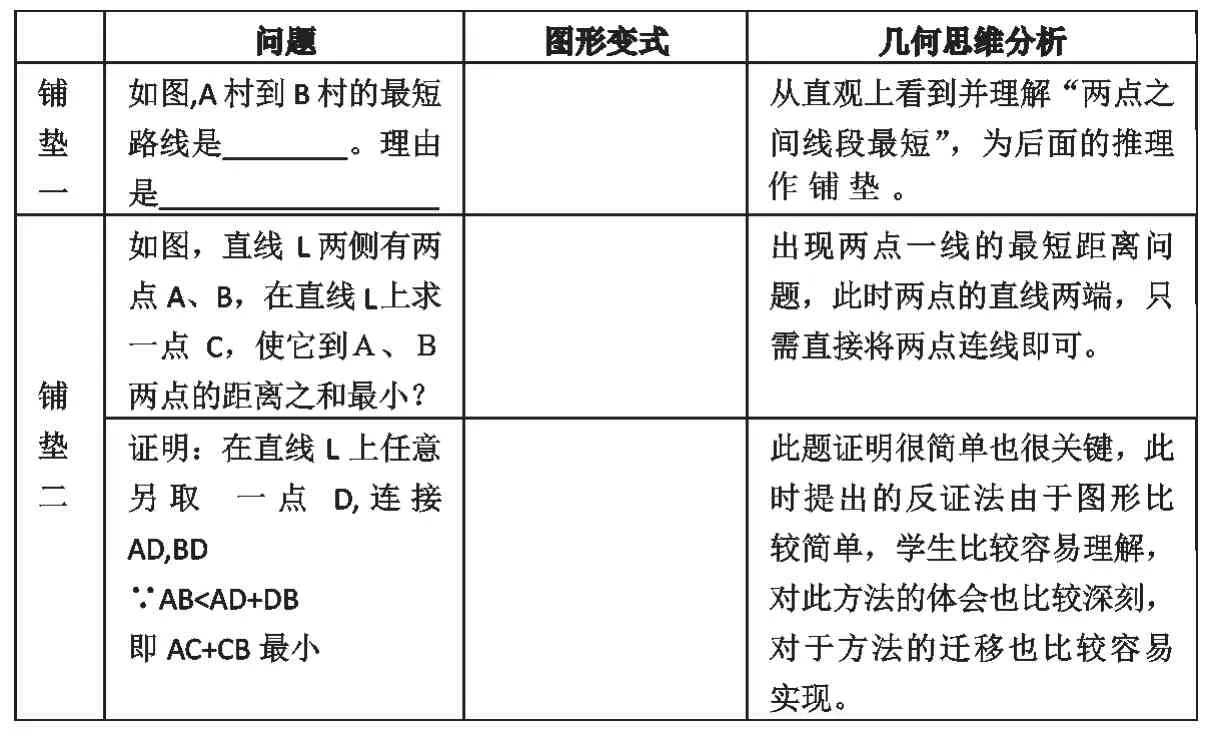
学生的几何思维都是从直观到抽象，从简单到复杂。但是学生的思想方法同时也具有迁移能力，如果我们可以把问题分解，从简单到复杂，让学生逐步地感受逻辑推理的方法，尝试举一反三。因此，对于本文讨论的问题，在开始进行证明前，我设计了以下铺垫（见下表）。

对于启发式探讨，只有在它的每个步骤都容易实现的条件下才有可能，要使学生在寻求一个证明的下一个步骤的尝试上具有多样性并获得成功，也只有在他们能容易地看出这一步时才会实现。所以从简单的图形构建学生的思维、演绎证明方法，避免直接进入复杂的图形中，有利于学生对知识的理解与方法的迁移。

?

三、自我反思

这节课在增加了以上的铺垫内容后，学生掌握起来比较轻松，而且对于确定最短距离的原理、证明方法掌握得比较好。