偏置转向轴原地转向轮胎力学特性研究
2021-02-01周福阳郭康权党小选
周福阳 郭康权 李 岩 党小选
(西北农林科技大学机械与电子工程学院, 陕西杨凌 712100)
0 引言
温室、农产品仓储库等环境空间狭小且封闭,需要运动灵活、无废气排放的动力机械[1-3]。为此,本课题组研发了一种4轮毂电机独立驱动、4轮全向独立转向的柔性底盘[4-9],该底盘主要由4组相同的、转向轴与轮胎回转平面之间具有一定偏置距离、驱动转向合二为一的偏置转向机构组成,其结构简单,四轮独立驱动、独立转向,可以灵活地实现两轮转向、四轮转向、横行、斜行及原地回转等运动模式,便于在狭小封闭空间运行作业。
柔性底盘在进行原地回转与横行模式姿态切换时,车体不动,车轮绕偏置转向轴原地滚动转向。文献[10-14]对普通车辆原地转向时的轮胎模型进行了研究。但普通车辆原地转向与偏置转向轴原地转向时轮胎的运动并不完全相同,其模型也不适用。WEI等[15]对车轮转向力矩随车轮转速增加的变化情况进行了研究,并提出了新的动力学模型,但其研究的是车辆运动过程中车轮的转向力矩。宋树杰等[9]在试验台上对柔性底盘原地姿态切换时的电机特性进行了研究,发现轮胎受到较大的纵向力,但并未解释其原因,且其偏置距离固定不变。目前,尚未见对柔性底盘特有的偏置转向轴原地转向运动轮胎力学特性的研究报道。本文基于LuGre摩擦模型对偏置转向轴原地转向进行建模与试验测量,研究其力学特性,以期为柔性底盘转向驱动力矩的估算和转向装置参数的优化提供依据。
1 轮胎模型
1.1 偏置转向轴原地转向工况分析
柔性底盘样机如图1所示[6],其电磁摩擦锁定片与车架固连,动片、偏置转向轴(在轴承座内)及偏置臂三者固连。动片、偏置转向轴、偏置臂、电动轮等构成了车轮转向组。偏置转向轴(相当于普通车辆的主销)与轮胎回转平面之间有一定的偏置距离,摩擦锁锁紧时,车轮转向组和车体之间的相对位置不变,车辆保持直行或现有的运动状态;当锁紧力矩小于轮胎力相对偏置转向轴的力矩时,车轮转向组相对车体转动,车轮转向,车辆随之转向。
原地回转与横行是柔性底盘的两种灵活且重要的运动方式,二者皆由初始姿态切换而来,姿态切换时电磁锁解锁,两前轮正转,两后轮反转,从而车体不动,车轮转向(图2)。该过程车轮绕偏置转向轴原地转向,因此,明确其轮胎的力学特性,是柔性运动控制的关键和基础。相比于传统车辆,偏置转向轴原地转向时具有3方面特殊性:①轮胎回转平面与转向轴存在较大偏置距离(一般超过250 mm),轮胎绕偏置转向轴转向的同时还存在自转滚动。②转向动力源自轮毂电机,转向力完全来自轮胎滚动时受到的地面的反作用力。③轮胎转向角变化范围大,理论上可以360°,实际中也能超过135°。可见,偏置转向轴转向过程比较特殊,且受力状态较为复杂,需通过深入的理论分析及试验,明确其力学特性。
1.2 轮胎接地区域运动学分析
1.2.1接地区域纵向滑移速度
车轮前进时的轮胎滑移速度等于车速(车轮中心速度)与轮速(通过车轮角速度算出的滚动速度)的差。绕偏置转向轴原地转向时车轮边滚边转,将轮胎划分成一个个纵向列,各列中心的速度(相当于车速)与其到转向轴的距离成正比;而车轮作为一个整体,各列滚动速度(相当于轮速)相同。该矛盾造成各列接地区域滑移速度不同,靠近中间的某个列纯滚动,其外侧各列向前滑动,内侧列向后滑动。
图3为轮胎原地滚动转向示意图,图中的虚线显示的矩形为轮胎接地印记,在接地印记上定义接地区域的坐标,坐标原点为轮胎接地印记最前最内侧的点,坐标方向如图中所示。该坐标系随着转向组一起转动,为运动坐标系。设轮胎滚动转向过程中,纯滚动列的横坐标为l,该距离为稳定点距离,接地印记内侧到转向轴的距离为L,为胎边距离,则
rω=(L+l)φ
(1)
式中r——轮胎半径
ω——轮胎滚动角速度
φ——车轮转向角速度
接地区域中心到转向轴偏置距离为p,b为轮胎接地印记宽度,a为接地印记长度。则p=L+b/2。vX(x,y)为轮胎接地区域坐标为(x,y)的点的纵向滑动速度,纵向滑动以向X正向滑动为正,则
vX(x,y)=rω-(L+y)φ=(l-y)φ
(2)
由式(2)可知,接地区域上横坐标相同的点的纵向滑动速度相等。稳定点内侧接地区域向后滑动,外侧接地区域向前滑动。
1.2.2接地区域横向滑移速度
轮胎胎面的运动是在绕转向轴公转的基础上绕车轮轴转动,是两个运动的合成运动。图4a为轮胎接地区域绝对速度的合成。轮胎胎面运动的参考坐标系固定在车轮轴上,则参考坐标系的转动角速度等于φ,车轮滚动时接地区域上任意一点的牵连速度为(L+y)φ/cosθ,相对速度为rω,则纵向绝对速度为
(3)
因为地面静止,该速度即为轮胎纵向滑动速度。式(2)和式(3)一致,说明从两种角度得到的纵向滑移速度相同。
横向滑动以向Y正向为正,接地区域任意点的横向速度为
(4)
式(4)说明轮胎接地区域任意一点的横向滑移只和该点的纵坐标有关。纵坐标相等的点的横向滑移速度相等。轮胎前部向内侧横滑,轮胎后部向外侧横滑。根据式(3)和式(4)做出接地区域各点的滑移速度,如图4b所示。
1.3 偏置转向轴原地转向LuGre模型
1.3.1轮胎纵滑LuGre模型
轮胎模型中“魔术公式”等半经验轮胎模型精度较高,使用广泛,但需要拟合参数多,拟合难度大,并且参数物理意义不明确[16-18]。偏置转向轴原地转向时接地区域各点的横向滑移沿纵向中线对称(图4b),按照库伦摩擦(动摩擦力大小相等,方向与滑移速度方向相反),总的横向摩擦力应该为零,这与实测中横向摩擦力较大相矛盾。
LuGre摩擦模型由CANUDAS等[19]在Dahl模型的基础上发展而来,它是Dahl模型的扩展,同时采纳了鬃毛模型的思想,即在微观下接触表面可以看成是大量的具有随机行为的弹性鬃毛。该模型用一个1阶微分方程描述了诸多摩擦现象,较其他模型更能体现真实摩擦现象。该模型可以精确描述轮胎摩擦力的动态特性, 还具有数学形式紧凑与参数物理意义明确的优点。基于LuGre摩擦模型,学者们对轮胎滑移、滑移侧偏联合、以及原地转向等轮胎运动提出新的动态力学模型[11-12, 17-18, 20-24],证明了该模型在轮胎研究中的准确性。根据文献[20],分布式纵滑轮胎LuGre模型为
(5)
(6)
(7)
式中Fn(x,t)——接地印记上垂直载荷分布函数
σ0——轮胎刚度系数
σ1——轮胎阻尼系数
σ2——轮胎相对黏滞阻尼系数
z(x,t)——鬃毛的弹性变形量函数
F(x,t)——轮胎的摩擦力函数
uc——库仑摩擦因数(近似于滑动摩擦因数)
us——静摩擦因数
vr——接触面的相对运动速度
g(vr)——Stribeck摩擦模型函数[25],代表稳定状态下摩擦因数随滑移速度变化的函数
vs——Stribeck速度,取2.7 m/s
α——Stribeck指数,表示稳态摩擦特性,取0.5
1.3.2纵滑-横滑联合偏置转向轴原地转向LuGre模型
根据1.2节的分析,偏置转向轴原地转向时轮胎既有纵向滑移,又有横向滑移,并且每一处滑移情况都不相同,需要将单一的纵滑模型扩展到各处滑移情况不同的纵向-横向联合滑移模型。偏置转向轴原地转向LuGre模型鬃毛的变形应为x、y和t的函数,z记为z(x,y,t),该变形为矢量,也可以表示为两个方向的标量z*(x,y,t),*为x或者y,代表z在X或者Y方向的分量。变形量对时间的导数为
(8)
根据图3可知
x(t+Δt)-x(t)=rωΔt
(9)
y(t+Δt)-y(t)=0
(10)
式中x(t)——轮胎上某一点t时刻在接地印记的纵坐标
y(t)——轮胎上某一点t时刻在接地印记的横坐标
由式(9)、(10)可知,∂x/∂t=rω,∂y/∂t=0。当轮胎滚动速度不变时,轮胎接地印记上同一坐标的鬃毛变形量不随时间改变,即∂z*(x,y,t)/∂t=0。因此稳态时式(8)变为
(11)
假设轮胎沿任意方向的滑动摩擦因数不变,摩擦阻力的方向和相对运动方向相反,则
(12)
根据式(11)、(12),式(5)变为
(13)
根据式(1)、(3)、(4)、(13),轮胎的横向和纵向鬃毛变形方程为
(14)
(15)
式中σ0x——轮胎纵向刚度系数
σ0y——轮胎横向刚度系数
式(14)、(15)的解析解无法用初等函数表示,但可以求其数值解。初始接地点鬃毛变形量为零,因此变形量的边界条件为zx(0,y,t)=0,zy(0,y,t)=0。
因为∂z*(x,y,t)/∂t=0,式(6)变为
dF*(x,y)=(σ0*z*(x,y,t)+σ2*vr*)dFn(x,y,t)
(16)
根据式(16),当载荷Fn均匀分布时,轮胎纵向摩擦力Fx及横向摩擦力Fy为
(17)
(18)
轮胎受到的力相对于转向中心的力矩M为
(19)
式中σ2x——轮胎纵向相对黏滞阻尼系数
σ2y——轮胎横向相对黏滞阻尼系数
框架绕转向中心匀速转向,轮胎受到的纵向摩擦力和横向摩擦力绕转向中心力矩的和应为零,即匀速转向时M=0。式(17)~(19)中的Fx、Fy、M同样没有解析解,但可以求其数值解。求Fx、Fy的步骤为:先假设纯滚动列与内侧胎边距离l=b/2,求M的值,当M<0时,l增加Δl,再次求M值,反复这个过程,直到M>0。当Δl足够小时,M由负转正的l值将非常接近实际值,将该l值代入式(17)、(18),即可求得该情况下的纵向摩擦力与横向摩擦力的数值解。
2 试验装置与数据处理
2.1 试验装置与试验方法
测试装置机械部分实物与轴套滑块局部如图5所示,因为滚轮滑块可以绕水平轴转动,滑块轴套整体又可以绕偏置转向轴转动,因此直线导轨等组成的框架具有3个自由度,即绕水平轴与转向轴转动,以及沿滚轮滑块移动。轴套和后框架之间连接了拉压力传感器后,会限制框架移动,从而测出横向力。
主要仪器:玲珑155R13C型轮胎,胎压230 kPa;Campbell cr1000型数据采集器;轮毂电机母线电流传感器为华控兴业HKK-10I型直流电流变送器,量程为0~20 A,输出0~5 V电压信号,精度0.5%;车轮转数传感器为杰特仕增量型光电旋转编码器,360脉冲/转,通过齿轮变速后,车轮转动一圈输出1 800个脉冲信号,可保证低速时的采集精度;中诺ZNLBS型高精度拉压力传感器,量程0~100 kg,输出0~5 V电压信号,精度0.05%。
试验方法:试验设两个因素,轮胎垂直载荷与偏置距离。垂直载荷3个水平,分别为980、1 470、1 960 N。偏置距离4个水平,分别为0.35、0.45、0.60、0.80 m。共12个水平组合;每个水平组合重复做6组,其中3组轮胎绕转向轴顺时针转向,3组绕逆时针转向;每组转向圈数都超过6圈。测试量包括:轮毂电机的母线电流、车轮转速以及传感器输出横向力。
2.2 受力分析与摩擦力计算方法
为了根据测得的试验结果计算轮胎实际受到的横向摩擦力和纵向摩擦力,需要对运行过程中的框架和车轮进行受力分析,如图6所示。
2.2.1加载及实际载荷分析
通过在配重架上加减配重调节载荷,其静止时的值可以通过将框架升高,轮胎放置到电子秤上,调平后测量。
转动过程中的载荷通过框架受力主视图(图6a)分析。转向时框架不绕水平轴旋转,各力相对水平轴的合力矩为零,即
Fn=(mgS-Fyr)/p
(20)
式中m——框架加配重等转向物体的总质量
S——总质量重心到转向轴的距离
静止状态时Fy等于0,Fn=mgS/p。当轮胎转动时,因为Fy增加,Fn会减少,即转向过程中的实际载荷小于静止载荷。偏置距离越小,载荷变化越大。考虑到测得的横向力最大为643 N,车轮转动过程中载荷的变化不可忽略,因此仿真过程中的载荷要按式(20)算出的实际载荷计算,接地印记也要通过对初始载荷印记拟合得出。
2.2.2横向摩擦力分析
框架受力俯视图(图6c)反映了框架的各径向力。框架径向受到的力包括轮胎横向摩擦力Fy,框架及配重等的离心力FL,以及力传感器受到的拉/压力Fc,转向过程中没有径向运动,所以三者的矢量和为零,即
Fy=Fc-FL
(21)
每个时刻传感器测的压力减去相应时刻计算得到的离心力即可求得对应时刻的轮胎横向摩擦力。框架和配重等物体绕转向轴旋转,受到的离心力等于各部分离心力的和,计算方程为
(22)
式中s——各微质量到转向中心的距离
式(22)说明总离心力等于位于重心的等重质点的离心力,因此总离心力可通过测量计算。实际上因为重心距离短,转向角速度低,离心力只有几十牛顿,对整体横向摩擦力影响不大。
2.2.3纵向摩擦力分析
车轮转动时,轮胎受到的合力分析如图6b所示。各合力绕转动中心的力矩包括电机的驱动力矩Mq,由于支撑力Fn前移造成的轮胎滚动阻力矩Mz,以及大小等于Fxr的轮胎纵向摩擦力力矩。车轮匀速滚动时,合力矩为零,即
Fx=(Mq-Mz)/r
(23)
因此轮胎纵向摩擦力可以通过驱动力矩计算得出,驱动力矩可以通过在电机测试台架上对以同样转速、同样母线电流运转的同一电机测量得到。
轮胎滚动阻力系数取0.01[26],忽略转向时的载荷改变,在3种载荷下,滚动阻力矩分别为2.57、3.90、5.14 N·m。
在初始静止状态下,测量载荷980、1 470、1 960 N时对应的轮胎滚动半径r分别为0.267 8、0.265 3、0.262 3 m。
3 试验结果与分析
3.1 电流、转速与横向力测试数据
偏置距离0.45 m、载荷1 960 N时,其中一次的测试数据如图7所示,图中第1段试验轮胎顺时针转向,可以看到轮胎自转超过10圈,第2段逆时针转向,第3段顺时针转向。整个运行期间轮胎转速、电流和横向力虽有波动,但大致平稳。选取速度比较平稳之后,相同圈数的正转和反转的时间段进行平均,得到车轮近似匀速运动时的电机母线电流、转速和横向力。从图中可以看到,第1段和第3段虽然转速相差很多,但是平均横向力非常接近,实际上去除离心力后,两者的平均值几乎相等。所以横向力和车轮转速无关,但会受到转向方向影响,初步判断是因为制造误差,车轮轴的延长线不通过偏置转向轴,而是有1.5 mm左右的误差,导致顺时针和逆时针转向时横向力有一些差别。
3.2 LuGre模型参数辨识方法与结果
式(14)、(15)、(17)~(19)为轮胎LuGre动力学方程,需要对方程中的参数进行确定和识别。初始静止状态下接地印记尺寸a和b通过实测得到,其值如表1所示,转向状态下接地印记尺寸根据实际载荷拟合得到。转向角速度φ对最终结果影响很小,试验过程中其值在0.5~0.8 rad/s之间,取其平均值0.6 rad/s。因为轮胎转速很慢,σ2x、σ2y影响极小,都取0.001 8 s/m[18]。根据初步辨识,发现vs对结果影响较小,根据初步辨识结果取3.6 m/s。
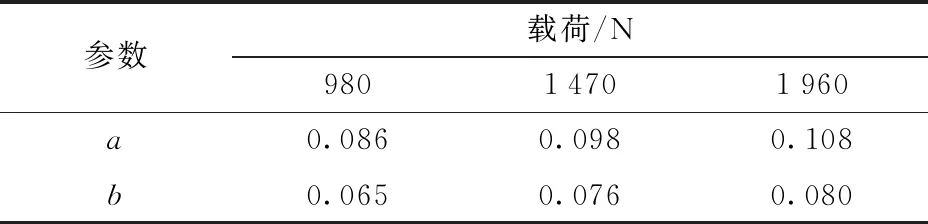
表1 不同静态载荷的实测接地印记尺寸Tab.1 Measured values of contact patch under different static loads m
方程中需要辨识的动态参数包括:σ0x、σ0y、us、uc。张鹏等[23]研究表明,上述4个参数随着载荷而改变。因此参数识别要按照载荷进行,但为了体现整体特点,忽略了转向时载荷的改变,同一初始载荷认为参数相同。
因为方程没有解析解,无法直接用最小二乘法辨识。为此将动力学方程作为一个黑盒,输入一组参数,根据1.3.2节的方法,可以求出其数值解与总加权二乘值,其中纵向摩擦力二乘值权重取25,横向摩擦力权重为1。参数辨识时,先根据现有文献,确定各参数的预设值;接着按照参数对结果的影响程度,轮流固定其余参数,辨识一个参数,几轮之后参数不再改变,即可认为是最终的辨识结果。预仿真表明,参数影响程度从大到小依次为us、σ0y、σ0x、uc。
对单个参数进行初步辨识的原理是以一定的步长增加该参数,当总二乘值减小时,说明调整参数方向正确,继续以原步长改变参数;当总二乘值增加时,说明步长方向错误,也说明已经靠近最佳参数,则步长变成原来的-1/2,。反复进行上述步骤,即可以倍增的精度找到最佳参数。
识别过程中发现,静摩擦因数影响较小;库伦摩擦因数对横向摩擦力影响巨大,对纵向摩擦力影响较小;横向刚度系数和纵向刚度系数对横向摩擦力影响很小,对纵向摩擦力影响较大。参数识别结果如图8所示。从图中可以看出,随着载荷增加,库伦摩擦因数和静摩擦因数变化很小,纵向刚度系数近似线性减少,而横向刚度系数随载荷变化呈非线性。
3.3 仿真与实测结果对比
纵向摩擦力的实测值和仿真值对比如图9a所示,图中显示的是力的绝对值,实际值为负值,表示其方向指向轮胎前方,阻碍轮胎滚动。从图中可以看到,实测结果和仿真结果基本一致;但也发现偏置距离较小时仿真结果大于实测结果,偏置距离较大时仿真结果小于实测结果,即仿真纵向摩擦力比实测值变化更快。这可能是因为偏置距离小时,实际载荷降低多,滚动阻力也应该同样降低,按滚动阻力不变计算的实测值较真实值小。
横向摩擦力的实测值和仿真值对比如图9b所示,图中横向摩擦力为正值,代表方向指向轮胎外侧。图中可见实测结果和仿真结果基本一致,相对误差较小。
3.4 柔性底盘原地姿态切换轮胎摩擦力仿真
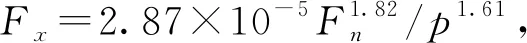
3.5 轮胎磨损
在试验过程中发现,原地滚动转向对轮胎有一定的磨损。图11为轮胎转向十多圈后在地面上留下的类似原地转向的磨损痕迹,从痕迹看,随着偏置距离的减小,磨损程度增加。偏置距离0.35 m时,即使只转过一圈,也会在地面上留下轻微的痕迹。
4 结论
(1)偏置转向轴原地转向过程中轮胎的力学模型可以用基于LuGre摩擦的轮胎模型表述。
(2)柔性底盘原地姿态切换时,受到阻碍轮胎滚动的纵向摩擦力。随着偏置距离的减小,纵向摩擦力迅速增加,其值与载荷的1.82次方成正比,与偏置距离的1.61次方成反比。
(3)柔性底盘原地姿态切换时,受到指向轮胎外侧较大的横向摩擦力。随着偏置距离的增加,横向摩擦力先增加、后减少,但变化较为平缓;随着载荷增加,横向摩擦力增加,其最大值对应的偏置距离增加。
