基于深层残差网络的山区DEM超分辨率重构

张宏鸣 全 凯 杨亚男 杨江涛 陈 欢 郭伟玲

(1.西北农林科技大学信息工程学院， 陕西杨凌 712100； 2.西北农林科技大学水利与建筑工程学院， 陕西杨凌 712100；3.安徽理工大学测绘学院， 淮南 232001)

0 引言

数字高程模型(Digital elevation model，DEM)[1]是将地表高程用数字形式表达的有序阵列，具有丰富的地学应用价值[2]，被广泛应用于水文分析、流域特征提取、城市规划等方面。DEM的精度决定了地学信息提取及分析的准确度[3]。受测量成本和技术限制，高精度的DEM较难获得[4-5]。卫星遥感是近年来获取高精度DEM的较好方法。采用航空摄影、SAR(Synthetic aperture radar)、光探测等技术获取DEM，在时间、成本和工作量上有着较大的优势[6]。无人机遥感技术由于设备体积小、操作简单、灵活性强等优势而被广泛应用于航空遥感、地面遥感、精准农业领域[7-8]。随着多种数据获取技术的发展，同一地区的遥感影像越来越多，具有多时相、多光谱、多分辨率的特点[9]。为了利用多源数据的互补性和合作性提取更加丰富的信息，学者们对数据融合技术进行了研究[10-11]。然而，由于安全性和保密性等原因，获取多源数据极为困难。近年来，对低分辨率DEM重构直接获取高分辨率DEM的超分辨率方法具有很强的可行性[12]。

DEM超分辨率方法的研究由来已久[13-16]。随着计算机技术和人工智能的发展，研究发现，基于学习的方法能够有效利用高效能计算机硬件的优势，抽象地学习到高低分辨率数据之间的映射关系，从而提高DEM精度[17]。文献[18]提出了非局部相似性的方法，利用测试区域同其他相似区域的关系重构DEM数据。文献[19]使用稀疏混合估计法对10、20、40 m的DEM进行重构变换，研究了超分辨率对黄土高原DEM坡度的影响。文献[20]设计了一种HNN神经网络，对20、60、90 m的格网DEM进行超分辨率重构，进一步提高了格网DEM的重构精度。文献[21]分析了几种卷积神经网络方法对DSM重构结果的影响，证明对于子像素级的DSM，超分辨率方法更易获取更高精度的数据。文献[22]提出了一种全卷积神经网络算法，对卫星高程数据和实地测绘数据之间的映射关系进行研究，提升了公共DEM的精度。传统端到端方法的网络模型设计简单，且运算快捷[23]。为了进一步提高结果的精度，有学者证明适度增加卷积网络层数可获得很好的效果[24]。但是，网络层数的增加意味着更大的计算量和更多的时间消耗，不适用于实时数据处理。有学者提出了残差学习思路，在网络训练时，只进行差值计算[25]。由于DEM高程往往较高，相对于普通图像在这种训练思路下获益更大。因此，深层残差卷积神经网络可能是提升DEM精度的有效方法。

梯田DEM在农业领域应用广泛。低分辨率梯田DEM的田坎、田埂等纹理过于模糊，不能准确表达实际地形特征[26]。通过超分辨率重构对梯田DEM的格网空间进行重新分配，能够获得更加精细和微观的梯田地理信息表达[27-28]。本文利用无人机梯田DEM数据，采用深层残差卷积神经网络对低分辨率梯田DEM进行重构，获取高分辨率DEM，并提取坡度。将高程结果和坡度结果分别与双立方插值法、稀疏混合估计法的结果进行对比，以证明本文方法具有更强的学习数据和获取地形特征的能力，以期为梯田DEM超分辨率重构方法的研究提供思路。

1 研究方法

1.1 研究区概况

以渝中地区龙泉乡黄土丘陵区典型旱梯田区为实验区，地理坐标为104°10′58″～104°19′51″E，35°34′4″～35°40′56″N，具有一定的代表性。该实验区DEM数据及其所在的黄土高原位置如图1所示，原始分辨率为0.5 m，高程为1 951.03～2 545.55 m。

由于不同区域数据高程差距较大。为了减小误差，使训练集适应大部分梯田数据。选取具有不同高程特点的实验样区1、2、3为训练样本集。其中，实验样区1整体高程较高，实验样区2整体高程适中，实验样区3整体高程较低。选取面积较大的实验样区4作为测试样本，地势整体起伏较大，覆盖高程范围广，能测试出更准确结果。样本区域如图2所示。

1.2 重构算法

卷积神经网络是一种基于卷积运算的前馈神经网络，通过对大量样本的有监督学习，将数据抽象化，并将特征提取的过程隐含在网络中[29]。深层的卷积神经网络结构可以加深层与层之间的联系，更好地学习到复杂的网络模型，提高网络对高频信息的表达能力[30]。本文将输入数据预插值到重构尺寸，通过对数据的训练，学习高低分辨率数据之间的映射关系，进而重构出高频信息来达到重构效果。

1.2.1算法流程

整个算法流程可描述为：①对原始训练样本进行重采样，生成低分辨率数据集，将二者混合得到高低分辨率样本集。②对高低分辨率样本集进行预处理，完成训练数据集准备。③控制神经网络结构，生成深层残差卷积神经网络。④对训练数据进行特征提取，选取合适的损失函数对其训练得到最优模型。⑤输入测试数据，使用最优模型对其进行重构。⑥将输出的数据转换为DEM数据格式(ASCII码)。⑦从高分辨率DEM数据中提取坡度。整体算法流程图如图3所示。

1.2.2网络结构

使用一种深层的残差网络[31]进行训练，这种残差学习方法可以缓解加深网络层数带来的梯度爆炸问题，并有效减少整个网络的参数。采用一种跳跃连接结构，假设y为映射目的层，x为输入层，则残差函数表达为

F(x)=y-x

(1)

此时，原始函数可定义为

y=F(x)+x

(2)

在每一次卷积操作后对输出进行补零操作，保证输入输出数据尺寸相同，忽略偏差值，则整个残差网络可用数学公式表达为

H(x)=F(x,{Wi})+x

(3)

整个网络共有22层。第1层处理输入数据特征，中间20层每层包含64个3×3×64的卷积核，最后一层包含1个3×3×64的卷积核。将原始低分辨率DEM进行双立方插值预处理到目标尺寸，输入模型中得到高分辨率DEM。

用ReLU激活函数[32]对每次卷积的结果进行非线性拟合，相比于其他激活函数，由于其一定的稀疏性，能更好地拟合训练数据。同时，其单侧抑制性实现了对信号的部分响应，提高了训练速度，公式为

σ(x)=max(0,x)

(4)

1.2.3损失函数

文献[33]表明使用平均绝对误差(Mean absolute error，MAE)损失函数训练得到的结果较好，故本文使用MAE损失函数进行DEM数据训练。

用均方根误差(Root mean square error，RMSE)作为重构准确性评价标准，值越小，说明重构后的DEM结果相对于真实数据的差距越小，更加符合真实梯田地形地貌特征。

2 实验结果与分析

为了更清楚地展示重构结果，本文截取了局部DEM及其坡度计算结果，将深层残差网络法(Very deep convolutional networks super-resolution，VDSR)结果分别与双立方插值法(Bicubic interpolation，CUBIC)[34]、稀疏混合估计法(Sparse mixed estimation，SME)[35]进行对比评价。用作差法、频率曲线法和RMSE指标对结果进行统计分析，进一步验证重构结果。

实验中对原始测试数据进行双立方插值之后得到对应的10、20、40 m的低分辨率数据。将该3种分辨率的数据采用不同方法重构成相应的高分辨率数据(5、10、20 m)，从重构后的数据中提取坡度数据并与实际坡度数据进行对比。40 m到20 m的重构称为R20，20 m到10 m的重构称为R10，10 m到5 m的重构称为R05。

对于深层残差卷积神经网络训练方法，将高低分辨率DEM数据进行切割和旋转操作，混合所有样本共340个，挑选30个梯田特征较明显的数据作为测试集。设置基本学习率为1×10-5，模型使用Adam优化方法，设定β1=0.9，β2=0.999，ε=1×10-8。训练134 000次得到最佳模型。实验使用Caffe、Matconvnet实现，用NVIDIA M4000 GPU进行训练。

2.1 DEM空间分布结果

为了更好地展示实验结果，将测试样本(实验样区4)的典型梯田区域局部放大。3种方法生成的不同分辨率DEM和实际高分辨率DEM(Origin digital elevation model,OD)如图4所示，从上到下的3行数据依次为R05、R10、R20的计算结果，颜色由绿变红表示高程由低变高。

2.2 坡度空间分布结果

从DEM数据中提取坡度结果，由3种方法生成的不同分辨率DEM提取到的坡度结果和实际高分辨率坡度数据(Origin slope,OS)如图5所示，3行数据从上到下分别为R05、R10、R20的计算结果，颜色由绿到红表示坡度由平缓变陡峭。

随着分辨率的升高，3种方法提取到的坡度整体精度得到提升，并且与实际结果逐渐接近，其中深层残差网络法在3种分辨率条件下均最好。

在不同的分辨率情况下，深层残差网络法提取结果在空间分布上明显好于其他方法，尤其在较为平坦区域(田面)和较为陡峭区域(田埂)的重构结果，能够提取到空间分布更加精确的纹理效果。

在分辨率较低情况下，深层残差网络法仍能保持相对较好的空间线条。

2.3 计算结果统计分析

以R05为例，将双立方插值法、稀疏混合估计法、深层残差网络法提取到的DEM数据分别同实际5 m DEM数据作差，结果如图6所示。

双立方插值法、深层残差网络法的DEM差值结果表现为田坎、陡坡处误差较大，田面处误差较小。稀疏混合估计法出现了误差分布不一的情况，与数据本身的相关性并不大。

以R05为例，将3种方法提取到的坡度计算结果分别同实际5 m坡度数据作差。结果如图7所示。图像颜色绿色区域占比越大，该处理方法误差越小，效果越好。

从图7结果可以看出，双立方插值法、深层残差网络法在田坎、陡坡处误差较大，而田面处重构效果较好。稀疏混合估计法的误差并未集中在某一类区域，整体分布较为分散，在田面处也出现了效果不好的现象。

深层残差网络法的坡度误差很少会出现较长的连续条状纹理，其误差均集中在坡度较高的梯田区域，面积占比更大的田面区域绝大多数重构误差低于5°。

将各方法结果同实际结果作差，计算DEM差值频率和DEM累计差值频率分布如图8所示。深层残差网络法的高程误差在0.5 m以内的区域占到了98.3%，稀疏混合估计法的高程误差在0.5 m以内的区域占到了97%，与双立方插值法接近。

将各方法结果同实际结果作差，计算坡度差值频率和坡度累计差值频率分布如图9所示。从曲线图中可以看到，3种方法均为深层残差网络法效果最好。与实际结果相比，深层残差网络法95%以上的区域误差在5°以内，稀疏混合估计法93%区域误差在5°以内，而双立方插值法的这个比例在90%以下。

根据表1的差值结果分析，3种方法的高程和坡度误差最小值均为0。由最大值来看，深层残差网络法的高程误差和坡度误差的最大值最小，而其他方法会造成误差局部过大情况。就高程平均值来看，深层残差网络法与稀疏混合估计法相同，好于双立方插值法。深层残差网络法在坡度误差平均值上好于稀疏混合估计法和双立方插值法。

由表2的RMSE结果可知，深层残差网络法在高程和坡度结果上与实地数据偏离最小。

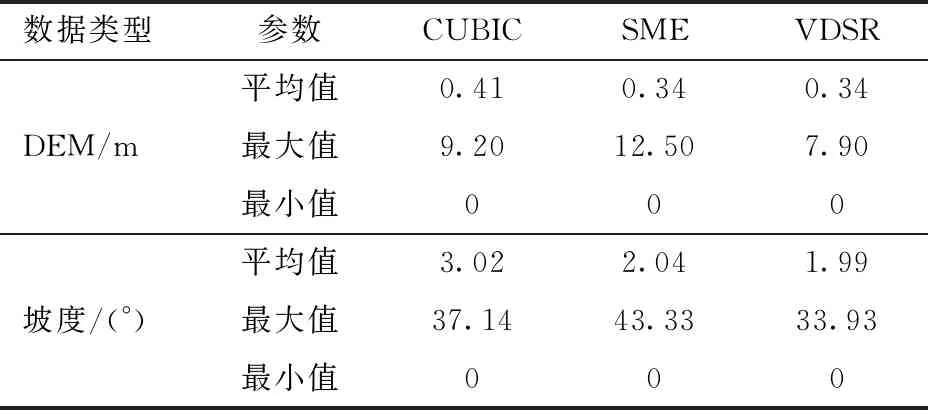
表1 差值结果Tab.1 Difference result

表2 RMSE结果Tab.2 RMSE result

根据耗时时间分析，稀疏混合估计法处理时间为663.39 s，而深层残差网络法处理时间仅为2.16 s，较稀疏混合估计法提升了300多倍。双立方插值法计算较为简单，处理时间为0.052 s，消耗时间最少。深层残差网络法在处理时间上具有较大优势。

3 结论

(1)针对常规的DEM超分辨率重构方法精度不高、难以满足实际需要的问题，提出一种卷积神经网络方法对DEM进行超分辨率重构，并分别在DEM结果和坡度结果上与传统插值法(双立方插值法)和浅层学习法(稀疏混合估计法)进行对比分析。通过实验验证，本文方法在DEM上的差值平均值和RMSE结果分别为0.34、0.486 9 m，较其他方法均有所提升。在坡度上的差值平均值和RMSE结果分别为1.99°、2.738 7°，比其他方法的地形数据结果更加接近原始地形。处理时间仅为2.16 s，比浅层学习法提升300多倍。

(2)在多源数据难以获得的现实情况下，利用多分辨率DEM数据之间信息的互补性，结合适当的深层网络设计，可以更好地映射原始数据与结果数据之间的关系。采用残差网络学习方法，可以降低训练难度。深层残差网络方法能够有效提高DEM精度，为获取高分辨率DEM提供了新的思路。