一个含有理分式核的Hilbert积分不等式
2021-01-30有名辉
台州学院学报 2020年6期
有名辉,孙 洁
(浙江机电职业技术学院 数学教研室,浙江 杭州 310053)
0 引言
不等式理论在数学中占有重要地位,它几乎渗透了数学的所有领域。自从德国数学家Hilbert在20世纪初提出了著名的Hilbert不等式后,100多年来,数学家们对它进行了深入的研究,取得了举世瞩目的新成果。这些新成果已经形成了一个庞大的理论体系,对数学自身和其他应用学科的发展具有重要的理论价值和应用价值。经典的Hilbert积分不等式通常可叙述如下:
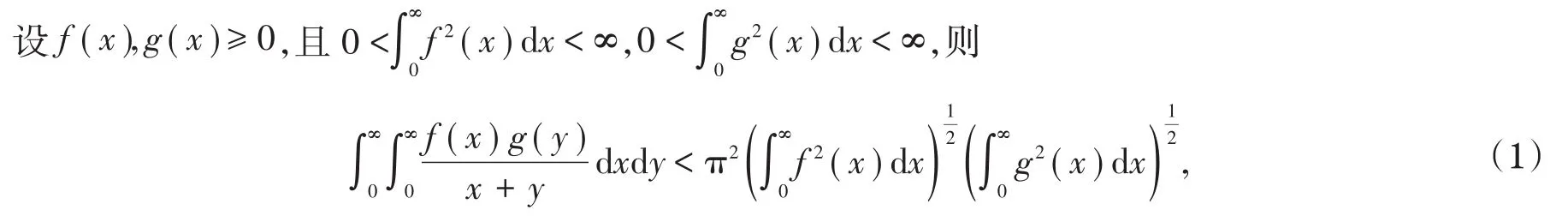
其中π2是满足式(1)的最佳常数因子[1]。近几十年来,通过引入参数,并考虑离散型,半离散型,研究者们给出了式(1)大量的推广、加强和类比。如文献[2]建立了

其中β>0,r+s=1。其他的一些相关成果可参见文献[4~13]。值得指出的是,对Hilbert型不等式的推广,最常见的方式是对指数或系数加入参数,在此仅从初等数学中“因式分解”的角度,构造一个新的核函数:
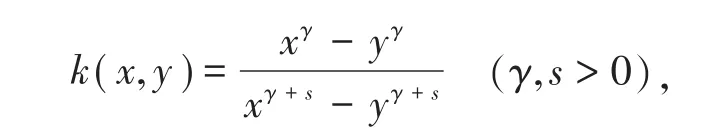
1 主要结果



2 结语
通过初等的方式,引入恰当的参数,构造一个分式型的积分核函数,并通过正切函数的有理分式展开,建立了一个新的Hilbert型积分不等式,推广了经典的Hilbert不等式。在核函数的构造上,较以往的文献均有所不同与创新;在最佳常数因子的处理上,采用了有理分式展开这一新的方法,具有一定的理论价值,并对其他类似的Hilbert型积分不等式的研究有一定的借鉴意义。
