高温冻土剪切力学特性试验研究

朱锋盼

(深部岩土力学与地下工程国家重点实验室(中国矿业大学)，江苏 徐州 221116)

青藏高原多年冻土面积约为1.5×106km2，约占中国多年冻土面积的70%[1]。高温冻土[2]又称塑性冻土，指含有较多的未冻水(常超过全部孔隙水的一半)而具有黏滞性和较大可压缩性的冻土。高温冻土温度处于-2～-0.5℃，是一种由土、冰、未冻水和空气等多相介质组成的复合多孔材料，温度的微小波动，都会引起冻土中未冻水含量发生较大变化，从而导致冻土力学性质产生明显的变化[3]。研究表明，受全球变暖的影响，到2050年青藏高原的温度将升高2.2～2.6℃[4]，温度的升高势必影响青藏高原冻土地区[5]。随着西藏自治区进一步的发展，需要基础设施的建设，包括高速公路、输电线路工程、管道工程[6]，这些工程的建设都涉及到高温冻土的剪切力学特性。

W.D.Roggensack等[7]、H.А.Цытович[8]、吴紫汪等[9]、沈忠言等[10]通过研究得出，冻土的抗剪强度是由冰和土颗粒胶结后形成的黏聚力和内摩擦角所组成。近年来，对高温冻土的剪切力学开展了很多的研究。曲广周等[11]对高温冻结粉质黏土进行了直剪蠕变试验，得到了冻结粉质黏土剪切蠕变曲线。黄元生等[12]进行高温冻土的直剪快剪的蠕变试验，得到了不同土质、含冰量以及密度类型的冻土剪切蠕变特性。张宏[13]研究了高温冻结黄土单轴抗压强度、抗剪强度和冻胀性随温度的变化规律。

基于此，本文取青藏地区3种典型原状冻土(粉质黏土、粉砂、细砂)，室内重塑为3种含冰量(饱冰、富冰、多冰)、2种不同密实程度(密实、松散)的试样，开展-2℃条件下的冻土直剪试验，分析不同土性高温冻土的剪切应力-应变曲线特性和强度变化规律，并探讨影响抗剪强度指标的主要因素，为高温冻土区工程建设提供参考。

1 试验方案与试样制备

1.1 试验方案

综合考虑原状土密度(ρ)、含冰量(质量分数:w)实测结果以及《冻土地区建筑地基基础设计规范》(JGJ118-2011)，确定试验粉质黏土含冰量分别为42%(饱冰)、28%(富冰)、22%(多冰)，相对密实状态下的干密度(ρd)分别为1.13、1.41、1.56 g/cm3(相对松散状态下的干密度分别为0.92、1.17、1.31 g/cm3)；粉砂和细砂则采取质量分数为45%(饱冰)、28%(富冰)、18%(多冰)的含冰量，相对密实状态下的干密度分别为1.06、1.21、1.33 g/cm3(相对松散状态下对应的干密度分别为0.86、0.98、1.08 g/cm3)。土样的颗粒级配如图1所示，物理参数如表1所示。

表1 土样其他物理参数Table 1 Physical parameters of tested soil

图1 土颗粒级配曲线图Fig.1 Soil grain gradation graph

1.2 试样制备

1.2.1 计算土、水、冰的质量

根据欲制试样的密度、含冰量，计算出制备一定数量试样所需要的重塑土质量、水的质量和冰的质量(冰质量∶水质量=2∶1，试验的过程中可根据实际操作的难易进行细微调整，但必须保证干土样的湿润，否则速冻时很难保证土冰颗粒的粘结)。

1.2.2 称量所需土、冰、水的质量

a.重塑土预先放入冰柜中冷却至负温(避免土冰混合时正温土样融化冰颗粒)，称量时精确至1 g。

b.将先前蒸馏水冻结的冰块在冷库中(冷库的温度设为-4 ℃)砸碎，并过1 mm的筛制成冰晶，称量冰晶时精确至1 g。过筛后冰晶颗粒如图2所示。

图2 冰晶Fig.2 Picture showing ice crystal

c.为保证搅拌过程中水加入的均匀性，用喷壶喷洒水，同样称量时精确至1 g。

d.搅拌土、冰、水三者的混合物至潮湿状。在冷库中，将冰晶和预先冷却的干土放入塑料盆中充分混合，再将一定质量温度接近0℃的蒸馏水喷洒加入冰-土混合物中，并不断搅拌均匀至潮湿状(手捏不分散，可成团即可)。

e.击实成样。将根据环刀的容积将要求天然密度所需质量的湿土(称量时精确至0.1 g)倒入环刀内，采用击样法，分3层击实到所需密度(即环刀被填满)。

f.冻结土样。将制好的试样用塑料密封袋封装，并立即放入冰柜中(温度为-10℃左右)快速冻结24 h以上。并将冻结时间达到24 h的重塑土试样放入冷库中(冷库温度为-2℃)，恒温 48 h后进行直剪试验。

1.3 试验方法

本次试验在多功能冻土模拟厅进行，所有试验设备均在-2℃环境中进行重新率定。试验采用EDJ-1型等应变直剪仪，刚环量程1 MPa，剪切速率为0.8 mm/min，法向应力分别为100、200、300、400 kPa。当剪切位移达到6 mm时，认为土样已经破坏，破坏的试样如图3所示。

图3 试验后的试样Fig.3 Picture showing sample after direct shear test

2 试验结果及分析

2.1 剪切位移-剪应力曲线

2.1.1 密实状态

典型密实状态下冻土剪切位移(Δs)-剪应力(τ)曲线形态如图4所示。通过分析可知，对于所有的密实状态下的重塑冻土，其Δs-τ关系曲线的一般形态可以描述为：在0 mm≤Δs<2 mm时，剪应力随剪切位移的增加急剧变大，曲线斜率初始段较大；在2 mm≤Δs≤4 mm时，剪应力随剪切位移增加的速率逐渐变小，剪应力逐渐趋向于一个定值，这在Δs-τ关系曲线形态上表现为曲线变缓；在4 mm<Δs≤6 mm时，冻土将出现峰值强度τf，随后随着剪切位移的逐渐增大，剪应力将稳定一段时间最后逐渐变小，在Δs-τ关系曲线上表现为应变软化的特征。

在现有的研究成果中，对于应变软化型土体的应力-应变数学描述的函数形式比较多。其中何青峰等[14]通过对马兰黄土的室内CU试验研究后提出，应变软化型土体建议采用如下指数函数进行应力-应变关系描述，即

图4 典型密实状态下冻土直剪Δs-τ曲线Fig.4 The shear displacement (Δs)-shear stress (τ) curves of frozen soil under dense state

σ1-σ3=a(1-e-b ε1)

(1)

式中：a、b为试验参数，a=(σ1-σ3)ult为三轴强度的极限值。

然而，通过仔细比较发现，重塑冻土直剪时其Δs-τ关系曲线与马兰黄土CU剪切应力应变曲线在形态上还是存在着明显差别的，主要表现在冻土直剪时其Δs-τ曲线上剪应力从0逐渐增大至稳定值τf的形态较马兰黄土要更为平缓，剪应力开始稳定时的应变量达6.5%左右，较马兰黄土的要大。同时通过利用(1)式对冻土直剪试验数据进行处理发现，试验值与计算值的偏差较大。因此，对重塑高温密实冻土直剪的Δs-τ关系描述提出了如下改进的指数函数形式

τ=a(1-e-b Δs2-c Δs)

(2)

式中：a、b、c均为试验参数，a=τf为直剪试验中抗剪强度值。

取直剪试验得到的冻土剪切强度的极限值a=τf，令R=τ/τf，将(2)式经过变换可以得到

ln(1-R)=-bΔs2-cΔs

(3)

将直剪试验Δs-τ曲线峰值前的试验值τ绘在ln(1-R)-Δs坐标系中，通过二次函数拟合得一条通过原点的二次抛物线，按拟合方程确定模型参数b、c值。

指数函数典型拟合曲线如图5所示，图中实心点代表试验值，空心点代表拟合值。

2.1.2 松散状态

典型松散状态下Δs-τ曲线形态如图6所示。通过分析可知，松散状态下冻土直剪的Δs-τ曲线形态与密实状态下存在着很大区别。主要表现在2 mm≤Δs≤4 mm阶段中曲线的斜率较密实状态下相应阶段的都要大，亦即2 mm之后剪应力随剪切位移增加而增加的速率较密实状态下衰减的要慢；同时在4 mm<Δs≤6 mm阶段中，松散冻土直剪的Δs-τ曲线大多不出现台阶状应变屈服硬化，应力仍以较大的速率随剪切位移的增加逐渐增大，直至试样最后破坏，在Δs-τ曲线形态上表现为应变硬化特征。

同时，通过比较不同含冰量松散冻土的Δs-τ曲线发现，随着含冰量的减少，冻土直剪Δs-τ曲线表现出应变硬化特征更为明显。这主要归因于随含冰量的减少，土颗粒之间的胶结能力减弱，随着剪切位移的增大剪应力不出现屈服软化阶段而直接发生破坏。

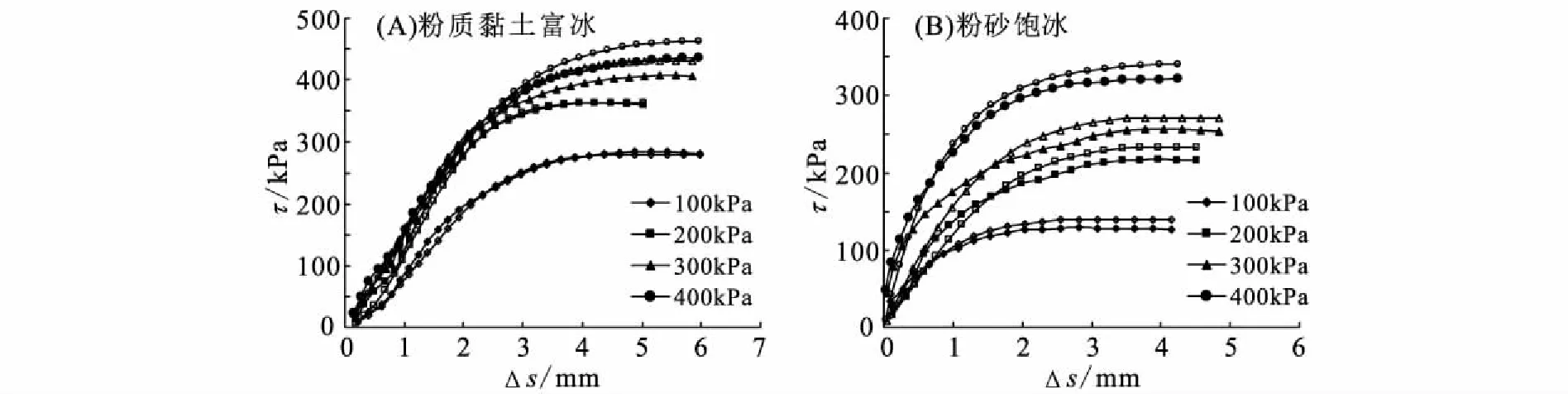
图5 利用指数函数拟合的曲线Fig.5 Curves fitted by an exponential function

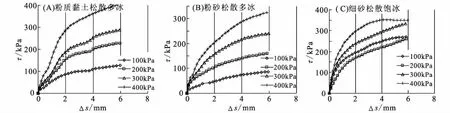
图6 典型松散状态下冻土直剪Δs-τ曲线Fig.6 Δs-τ curves of frozen soil under loose state

重塑冻土松散状态下Δs-τ曲线的形态基本上都呈应变硬化型的双曲线分布，因此，可以考虑用邓肯-张双曲线模型来描述其应力-变形关系特征[15]。邓肯-张双曲线模型在直剪试验中的一般表达式如下

τ=Δs/(a+bΔs)

(4)

式中：τ为剪应力；Δs为剪切位移；a、b为试验常数；a=1/Gi；Gi为初始剪切模量；b=1/τf。

(4)式也可以写成

Δs/τ=a+bΔs

(5)

在对数坐标中点绘lg(Gi/pa)与lg(σ/pa)的关系，则近似为一直线。pa为大气压力，引入pa是为了使纵横坐标化为无因次量。直线的截距为lgK，斜率为n，于是有lg(Gi/pa)=lgK+nlg(σ/pa)，由此得

Gi=Kpa(σ/pa)n

(6)

另外，定义Rf=τ/τf为破坏比，反映直剪试样强度发挥的程度。

根据重塑松散冻土直剪试验数据，经过回归拟合，得到邓肯-张模型中c、φ、K、n、Rf五个参数值(表2)。

表2 松散冻土邓肯-张模型参数值Table 2 Parameters of Duncan-Chang model for frozen soil under loose state

模型参数中c、φ值汇总于图8中。

通过以上对高温冻土直剪的Δs-τ曲线特征分析可以看出，高温冻土直剪时，在密实状态下应力-变形曲线形态表现为应变软化型特征；而在松散状态下则表现为应变硬化型特征。利用指数模型和邓肯-张模型可以分别对密实和松散状态下高温冻土直剪的应力-变形曲线特征进行描述。

2.1.3 原因分析

高温冻土直剪时，在不同密实程度下所表现出来的应力-变形曲线形态上的差异性，主要归因于不同密实程度下冻土的密度相差较大。

在密实状态时，因试样密度较大，制样过程中被充分压密，那么冻土试样内部的土颗粒在冰晶的胶结作用下相互紧挨，试样内部孔隙较少。直剪试验刚开始时，因试样足够密实其强度较高，在Δs-τ曲线形态上表现为剪应力随剪切位移的急剧增大；随后因试样内部裂隙少，剪切面上贯通裂缝的发展比较困难，从而试样出现被再度压密的过程，剪应力随剪切位移的增加出现屈服硬化，在Δs-τ曲线形态上表现为剪应力的平缓稳定阶段；随着剪应力的不断施加，最终试样被剪坏，表现为剪应力随剪切位移的增大而变小，在Δs-τ曲线形态上表现为曲线末端的下降趋势。

在松散状态时，试样密度较密实状态下的要小，稍加紧压环刀中的混合料即可填满。据此可以推断，松散冻土试样内部的孔隙较多，颗粒间距较大。直剪试验过程中，随着剪应力的不断施加，在剪切面的最薄弱面上内部孔隙将相互贯通形成通缝，最终导致试样被剪坏；而不会出现试样的再度压密过程，在Δs-τ曲线形态上表现为剪应力随剪切位移的增加不断增大，且不出现台阶状的平缓稳定阶段，应力-变形曲线呈现应变硬化特征。

2.2 抗剪强度

为消除试验过程中剪切面积不断减小带来的剪应力计算误差，采用(7)式对不同土性、含冰量、密度、温度条件下的冻土剪切数据进行修正

τ=CRA/A’

(7)

其中：τ为剪应力修正值(kPa)；C为量力环系数；R为量力环读数，0.01 mm；A为剪切盒面积，3 000 mm2；A’为实际剪切面积。采用半径r为30.9 mm的标准直剪试样，假设上下盒的相对位移(剪切位移)为Δs，则实际剪切面积

(8)

为了研究冻土的抗剪强度，还绘制了-2℃条件下纯冰的抗剪强度曲线(图7)。从图中可以得出，纯冰在剪切位移为2.5 mm时发生脆性破坏，黏聚力为688 kPa，内摩擦角为55.6°。

冻土的抗剪强度指标黏聚力c和内摩擦角φ，结果如图8所示。

已有研究[16-18]表明：冻土在低压条件下强度变化规律(σ<7 MPa)仍符合摩尔-库伦准则，而在较高压力条件下(σ>7 MPa)则符合抛物线准则[3]。本文试验压力σ≤400 kPa，故可以通过摩尔-库伦准则获取不同土性高温冻土内摩擦角和黏聚力随密度、含冰量的变化规律。

2.2.1 内摩擦角

相对松散状态下，不同土性高温冻土内摩擦角随含冰量的增加呈先减小后增加趋势。相对密实条件下，冻结粉质黏土、冻结粉砂的内摩擦角也表现出类似的规律，但不同土性之间内摩擦角先减小后增加的趋势略有差异，而冻结细砂的内摩擦角随含冰量的增加逐渐增加。即：当含冰量(w)<28%时，随土性中砂粒(粒径为0.075～2 mm)含量的增加，内摩擦角逐渐增加；当含冰量>28%时，随含冰量的增加，内摩擦角也逐渐增加。

图7 纯冰的Δs-τ曲线Fig.7 Δs-τ curves of pure ice

相同含冰量下冻结粉质黏土和冻结细砂的内摩擦角随密度的增加而逐渐增加，而冻结粉砂则刚好相反。另外从图7中还可以看出：在相对密实条件下，当密度相同时，冻结细砂的内摩擦角要大于冻结粉砂的内摩擦角。这是由于相同含冰量下细砂中的砂粒含量要高于粉砂，剪切过程中土颗粒与冰晶之间的摩擦加剧。由此推断，当含冰量继续增加时，冻结细砂的内摩擦角将超过冻结粉质黏土，也就是说随含冰量的不断增加，密度对高温冻土内摩擦角的影响程度变小。因此，相对密实状态下，当含冰量较低时(w<28%)，冻结粉质黏土的内摩擦角大于细砂和粉砂，而细砂的内摩擦角又大于粉砂；较高含冰量条件下(w>28%)，冻结细砂的内摩擦角超过冻结粉质黏土，且二者的内摩擦角均大于冻结粉砂。

图8 抗剪强度指标Fig.8 Shear strength parameters

2.2.2 黏聚力

不同土性高温冻土黏聚力随密度、含冰量变化规律呈现出3种趋势，即：持续增加，先增加后减小和先减小后增加，但规律性并不明显。结合图7可以获知，当含冰量较低时(w<28%)，冻结粉质黏土的黏聚力大于细砂和粉砂，而细砂的黏聚力又大于粉砂；较高含冰量条件下(w>28%)，冻结细砂的黏聚力超过冻结粉质黏土，且二者的黏聚力均大于冻结粉砂。

2.3 抗剪强度影响因素分析

2.3.1 土性

冻土的抗剪强度与土颗粒成分关系十分密切，当含冰量和密度相同，密实条件下，冻结细砂的黏聚力均要高于粉砂。其原因在于细砂颗粒级配中粒径>0.075 mm的粗粒的体积分数达91.6%，高于粉砂颗粒级配中的粗粒的体积分数(61.3%)，粗颗粒含量的增加导致冻结细砂的剪切强度远高于冻结粉砂。

粉质黏土颗粒级配中粒径>0.05 mm的粗粒的体积分数仅为15.5%。在含冰量及密度相同的条件下，其内摩擦角应小于二者；但因粉质黏土的密度较粉砂和细砂要大，从而导致其内摩擦角未必总是小于粉砂和细砂。多冰状态时，在同一含冰量的情况下，粉质黏土的密度要高于粉砂和细砂，从而其内摩擦角、黏聚力要大于粉砂和细砂，也即随着密度差值的增大(0.06～0.33 g/cm3)，在含冰量相同时，粉质黏土黏聚力和内摩擦角逐渐表现出超过粉砂和细砂的趋势。

2.3.2 含冰量

粉砂和细砂在不同含冰量状态下，其密度值接近，不同含冰量下的密度差异不大于0.03 g/cm3，从而控制其剪切强度的最主要因素为含冰量。

粉质黏土因不同含冰量试样之间的密度值同样差异较大(变化幅度达0.3 g/cm3)，在含冰量和密度二者之间的相互影响下，使得冻结粉质黏土抗剪强度随密度或含冰量的变化规律不明显。但在含冰量接近塑限(15.6%)时，试样密度最大，其内摩擦角亦达到峰值。

2.3.3 密度

对于粉质黏土和细砂，不同土类在密实状态下的剪切强度均大于松散状态下的强度，即相同含冰量下剪切强度受控于密度。而对于粉砂，含冰量相同时，松散状态下的内摩擦角要大于密实状态。

3 结论及展望

a.高温冻土直剪时，在密实状态下其应力-变形曲线呈现出应变软化特征，而在松散状态下则为应变硬化，可以分别利用指数模型和邓肯-张双曲线模型来描述高温冻土直剪应力-变形曲线。

b.在含冰量和密度相同的条件下，冻结细砂的剪切强度要高于冻结粉砂的强度；冻结粉砂的强度又要高于冻结粉质黏土的强度。但当冻结粉质黏土密度大于粉砂和细砂时，将出现强度高于粉砂和细砂的现象。

c.在密实状态时，冻结粉砂和细砂的黏聚力随含冰量的增加而增加；而在松散状态时，随含冰量的增加，其黏聚力逐渐增大，内摩擦角却逐渐变小。因粉质黏土在不同含冰量时密度差异亦较大，无论密实或松散状态，其抗剪强度随含冰量或密度变化的规律不是很明显；但在含冰量接近塑限时，内摩擦角达到峰值。

d.对于粉质黏土和细砂来说，在同一土性、同一含冰量的条件下，密实状态下冻土直剪的强度指标均要高于松散状态时的指标值。

本文仅对青藏地区3种不同土性高温冻土进行了不同影响因素下的试验研究，除此之外还应开展更为宽泛温度、含冰量以及密度条件下的剪切试验，并采取细观力学对不同土性剪切强度发挥机理进行研究，从而较全面地揭示高温冻土在不同试验条件下抗剪强度指标变化规律及影响因素。