PX装置吸附塔进料非芳含量的拉曼定量分析

蒋飘逸，戴连奎

(浙江大学工业控制技术国家重点实验室，浙江 杭州 310027)

1 引言

对二甲苯(PX)是工业中一种重要的有机化工原料，广泛用于生产纤维、树脂、橡胶等合成材料以及有机化工中间体和产品。PX生产过程主要以甲苯和C9芳烃为原料，使用甲苯歧化、二甲苯异构化等技术得到中间产物，其中包含混合二甲苯与少量非芳烃混合物；将中间产物作为进料，经吸附塔处理得到高纯度的PX成品[1]。进料混合物主要由PX、乙苯(EB)、间二甲苯(MX)、邻二甲苯(OX)构成，还有少量的非芳烃组分(NA)，内部可能包括直链烷烃和环烷烃等。若吸附塔的进料浓度波动较大，就会影响最终PX成品的纯度，且进料液组分情况复杂，因此需要选择合适的分析方法对进料各组分含量进行检测。

现阶段监测PX装置吸附塔进料液的组分含量的方法主要是气相色谱技术[2,3]和拉曼光谱技术[4]。使用气相色谱技术对芳烃进行定量分析，具有较高的灵敏度和精确度，但是无法满足快速性和简便性的检测要求，且其运行时的温度条件要求较高；拉曼光谱技术则具有响应速度快、无需样品前处理、建模所需样本数少的特点，而且其信号可以通过光纤远程传输，因此，采用拉曼光谱法对PX吸附塔的物料进行实时监测具有广阔的前景。

目前，运用拉曼光谱进行定量分析的方法主要分为基于统计学的回归算法和基于纯物质光谱的硬建模算法。回归算法中的偏最小二乘(PLS)算法[5,6]因为其准确度高、计算速度快而被广泛应用于定量分析。硬建模算法首先利用纯物质光谱等先验知识对混合物光谱进行分解，以得到各组分光谱的加权系数，并根据训练样本建立加权系数与各组分浓度的对应关系，从而进行定量分析。Marteau等[7]提出的经典的拉曼特征点分解方法，成功实现了对吸附塔循环液的在线远程监测；王斌等[8]采用了基于拉曼光谱线性叠加的谱分解技术，并准确地预测了PX吸附分离装置上的循环液中各组分的含量，预测标准误差在0.5%左右。

但是上述定量分析方法都只计算了主要芳烃组分的含量，而没有考虑混合液中的非芳烃组分。NA反映了一类物质，这类物质在进料中没有固定的组成，也无法获取其纯物质光谱。所以如何测量未知组分NA的浓度，是对进料液进行分析的难点。

为此，提出了一种基于分段光谱分解的进料液成分分析方法。针对对象特性，选取两段特征光谱。在1350 ～ 1550 cm-1谱段引入基于洛伦兹函数的拉曼光谱自动分解算法[9]，分解得到用洛伦兹谱峰拟合的NA组分的光谱分量及其峰面积，再在650～900 cm-1谱段基于直接光谱分析算法分解得到了EB、PX、MX、OX这四种主要组分的光谱分量及其对应峰面积。在此基础上，基于训练样品各组分的峰面积和浓度建立光谱定量分析模型。

2 实验部分

2.1 实验平台

实验平台如图1所示。使用中心波长为785 nm，发射功率为500 mW的激光器；采用定制的 785 nm 拉曼探头，该探头集激光发射与收集为一体，且光损耗率控制在20 %以内；选择TEC制冷光纤光谱仪，制冷温度在-20 ℃左右，能较好地抑制噪声；采样池中的比色皿为1 cm*1 cm的石英比色皿。

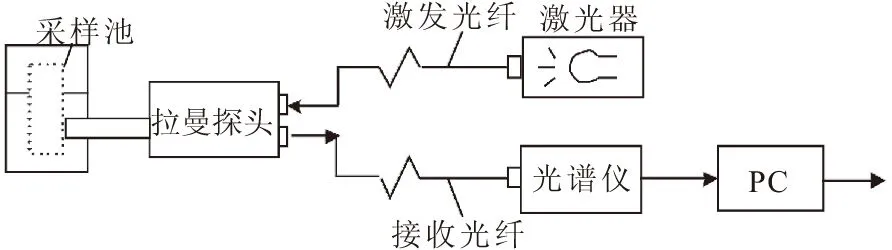
图1 拉曼分析实验平台Fig.1 Raman analysis experimental platform

2.2 样品配制

吸附塔进料液的主要成分包括EB、PX、MX、OX和NA。根据实际进料液各物质的浓度变化范围配制得到16个样品，其中以异己烷(iso-hexane)与正己烷(n-hexane)的不同配比来模拟不同组成的NA。各样品浓度如表1所示。

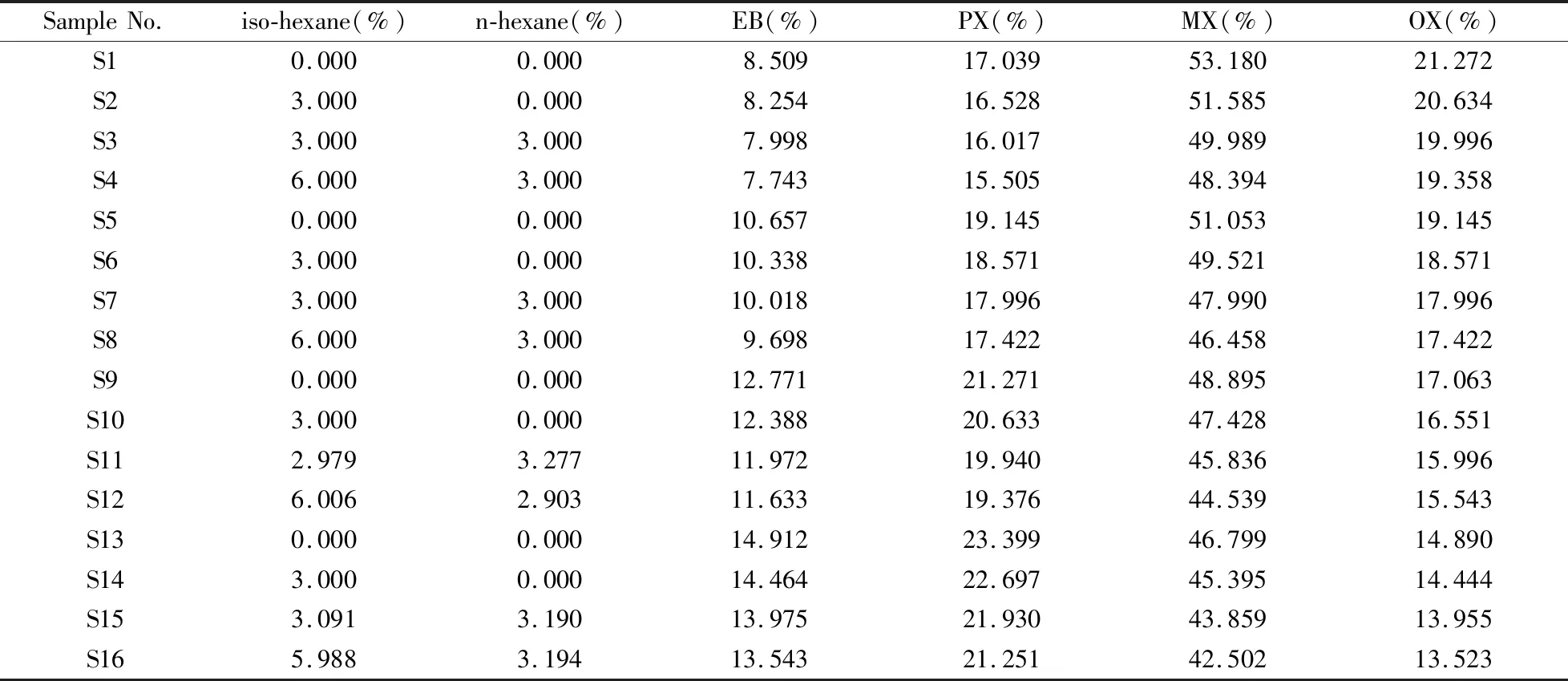
表1 混合液样品中各成分浓度配比Table 1 Concentrations of components in all samples

利用实验室拉曼光谱平台对16个混合样品及4种纯物质进行测量。混合液样品和纯物质样品的原始拉曼光谱分别如图2(a)和2(b)所示。

图2 (a)混合样品原始光谱；(b)纯物质样品原始光谱Fig.2 (a) Original Raman spectra of all samples;(b) Original Raman spectra of pure components

3 结果与讨论

3.1 样品拉曼光谱预处理

为消除测量条件波动对拉曼光谱的影响，需要对样品光谱进行预处理。由于荧光信号十分平缓，而拉曼信号较为尖锐，因此本文使用了迭代多项式平滑(IPSA)算法[10]进行基线校正，滤波宽度为150，迭代精度为10-6，终止区间为600～1800 cm-1。基线校正后的混合液光谱与纯物质光谱如图3所示。

图3 (a)基线校正后的混合样品光谱；(b) 基线校正后的纯物质光谱Fig.3 (a) Baseline corrected spectra of all Samples;(b) Baseline corrected spectra of pure components

3.2 未知非芳的光谱分解

对于进料样品，已知包含PX、EB、MX和OX这四种物质，还有少量的NA，而NA组分未知。所以需要利用拉曼光谱自动分解算法(参见附录)和四种纯物质光谱，对基线校正后的进料样品拉曼光谱进行分解，得到NA的拉曼光谱。

针对对象特性，选取两段谱峰进行光谱分解。烷烃类拉曼光谱的特征峰主要位于1451～1463 cm-1处[11]，且在这段中四种主要成分的光谱强度低，所以可以在1350～1550 cm-1段分解得到NA的光谱。由于四种主要成分的特征峰均位于650～900 cm-1中，其强度较大，可以近似认为这一谱段中没有NA光谱分量，且在这一段中谱峰相对独立，所以可以在650～900 cm-1段进行光谱分解得到PX、EB、MX和OX的分解系数，以提高分解精度。

分段光谱分解算法的步骤如下：

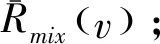
步骤2：输入该归一化进料光谱的1350～1550 cm-1段光谱和4条归一化纯物质光谱的对应谱段，利用拉曼光谱自动分解算法得到用洛伦兹谱峰拟合的NA拉曼光谱分量。归一化进料光谱可表示为如下形式：

(1)

步骤3：计算拟合得到的NA拉曼光谱分量的面积A5。

(2)

其中v1= 1350 cm-1，v2=1500 cm-1。

步骤4：输入该归一化光谱的650～900 cm-1段光谱和4条已知纯组分对应谱段光谱，利用硬建模算法得到PX、EB、MX和OX的拉曼光谱分量及各个分量的面积A1～4。归一化光谱可表示为如下形式：

(3)

以进料样品S4光谱为例，经过步骤2分解之后拟合的光谱如图4(a)所示，得到的主要成分光谱分量和用洛伦兹谱峰拟合的NA光谱分量如图4(b)所示。经过步骤4分解之后拟合的光谱如图5(a)所示，PX、EB、MX和OX的光谱分量如图5(b)所示。最后计算得到的各组分面积如表2所示。

图4 (a) S4样品光谱与拟合光谱；(b) 4种主要成分的光谱分量和与未知非芳光谱分量Fig.4 (a) Spectrum and fitting spectrum of sample S4;(b) Sum of spectra of four main components and spectrum of NA

图5 (a)S4样品光谱与拟合光谱；(b)4种主要成分的光谱分量Fig.5 (a) Spectrum and fitting spectrum of sample S4;(b) Spectra of four main components

表2 S4样品光谱经过分段光谱分解之后得到的各组分特征峰面积Table 2 Characteristic peak areas of each components of sample S4 after spectral decomposition in two regions

3.3 模型建立

基于上述算法可得到各混合液各组分的特征峰面积Ai。由于在进料混合液中MX含量均在40%以上，为了避免激光器强度波动引起的误差，使用各组分浓度与MX浓度之比作为相对浓度，使用各组分与MX特征峰面积之比作为相对面积。通过计算可得各组分的相对面积与相对浓度成正比，则有：

(4)

式中，ki为第i组分的比例系数，bi为截距；对于组分MX，kMX=1，bMX=0。

对于训练集，已知浓度xi，并由2.2中的分段光谱分解算法得到各组分面积Ai，再根据最小二乘法可求得每个组分的比例系数ki与bi。对于测试集，将求出的ki与bi代入，再结合所有组分的浓度之和为1，即可求得各组分浓度xi。

(5)

式中相对面积zi=Ai/AMX。

将样品分为训练集和测试集，选取8个样品作为训练集，估计得到的各组分相对于MX的相对含量模型系数如表3所示。对于某一测试集样品，在相同条件下测量其拉曼光谱，经基线校正与分段光谱分解，得到各组分的相对面积，通过式(5)计算得到该样品中各组分的浓度。

表3 估计得到的模型系数Table 3 Estimated coefficients in the models

3.4 模型评估与算法比较

为验证本模型的准确性，对8个测试集样品进行模型检验，并将本模型的分析结果与配样值进行比较。同时，针对同一批测试集样品，使用PLS算法、直接基于纯组分光谱分解算法[8]进行计算，比较三种方法的预测性能。

选择预测均方根误差(RMSEP)和预测复相关系数(R2)这两个指标作为模型的评价标准，如式(6)(7)所示。

(6)

(7)

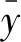
在PLS算法中，使用特征谱段650～900 cm-1和1350～1550 cm-1数据建模，根据分析将主元数设定为4。在基于纯组分光谱分解算法中，使用正己烷的纯物质光谱来表示NA光谱，在同一特征谱段进行光谱分解。

三种算法的预测结果比较如表4、5所示。可以看到，对于EB、PX、MX、OX这四种组分来说，三种算法的预测性能都很好，复相关系数均大于0.99；但是对于NA这个未知组分，本文方法的预测结果明显更好。由于本文方法用洛伦兹峰拟合得到了NA的光谱，所以与其他两种算法相比提高了预测性能。

表4 三种定量分析方法预测结果对比Table 4 Comparison of prediction results of three quantitative analysis methods

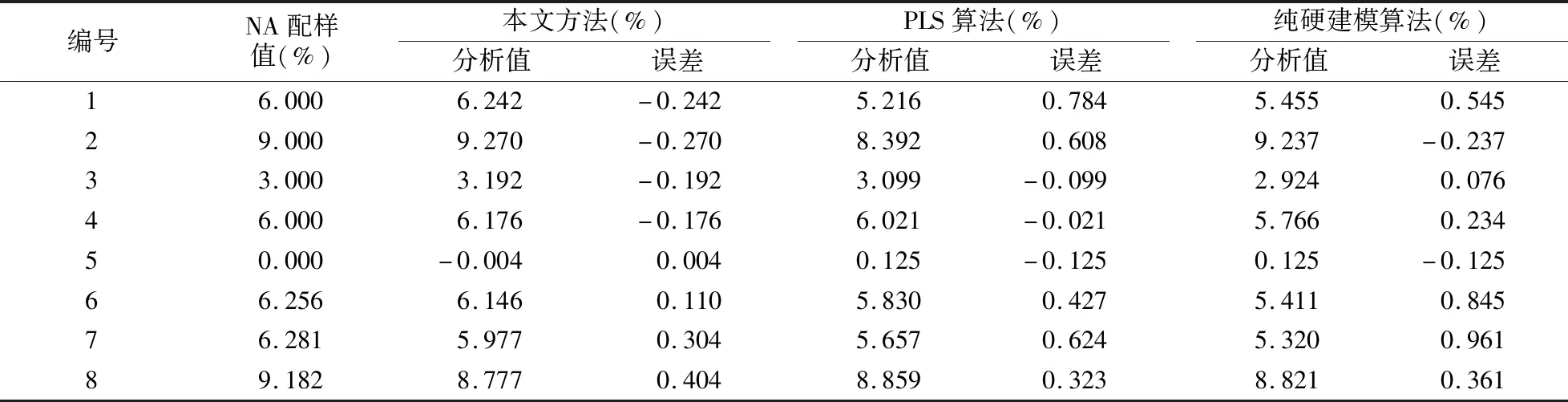
表5 测试样品中NA的实际配样值和三种方法预测结果Table 5 The actual value of NA in the test samples and the prediction results of three methods

4 结论

PX装置吸附塔进料液是一种部分组分已知的混合物体系，分析难点就在于其NA组分未知。为此，本文选取了两段特征光谱。对于特征谱段650～900 cm-1，基于直接光谱分解算法得到EB、PX、MX、OX这四种主要组分的光谱分量及对应的峰面积；而在NA光谱比例较大的1350～1550 cm-1段，结合洛伦兹函数的拉曼光谱自动分解算法分解得到NA组分的光谱分量及对应的峰面积。最后，基于训练样品各组分的峰面积和浓度，采用最小二乘建立光谱定量分析模型。实验结果表明，上述模型具有较高的预测精度，主要组分EB、PX、MX、OX含量的标准预测误差分别为0.13 %、0.20 %、0.24 %、0.13 %，复相关系数分别为0.997、0.993、0.992、0.997；而对于NA含量，标准预测误差为0.24%，复相关系数达到0.993，预测精度显著高于PLS算法与直接光谱分解法。本文提出的方法也适用于其他主要纯组分已知、但同时含有少量未知组分的混合物体系的定量分析。

5 附录

基于洛伦兹线型的拉曼光谱自动分解算法[9]就是将混合液光谱分解为已知纯物质组分的拉曼光谱以及拟合未知物质拉曼光谱的洛伦兹谱峰组，并且使得到的纯物质光谱分量与洛伦兹谱峰组之和能够最大程度地拟合原来的混合液光谱。

混合液光谱的数学模型可表示如下：

(8)

其中，β=α1,α2,…,αM,S1,c1,w1,S2,c2,w2,…,SN,cN,wN，v表示波数，M表示已知纯组分的个数，αi表示第i种已知纯组分的面积，Pi(v)表示第i种已知纯组分的面积归一化光谱，N表示光谱中的洛伦兹谱峰个数，Sk、ck、wk分别表示第k个洛伦兹谱峰的面积、中心位置与半宽。

对于混合液的光谱分解问题就等价于下列非线性最小二乘参数优化问题：

(9)

其中，Y(v)表示测量得到的光谱，以及v1，v2表示优化光谱范围的波数。

基于洛伦兹线型的拉曼光谱自动分解算法的主要思想为，在每次迭代中只在负偏差最大处增加一个洛伦兹谱峰，并且优化参数使得估计的光谱与原来光谱的误差最小，直至误差小于所规定的误差限σ时停止迭代。详细过程如下所示：

步骤1：输入一条预处理后面积归一化的混合液光谱Y(v)和M条已知的纯组分面积归一化光谱Pi(v)。设定纯组分光谱面积的初始值α=(α1,α2,…,αM)。

步骤2：利用非线性最小二乘法获得优化后的参数α。

步骤3：令优化参数β*=β=(α1,α2,…,αM)，并设定光谱误差阈值eps，K= 0。计算误差光谱r(v)=Y(v)-R(v,β)。

步骤4：令K=K+1。

步骤5：搜索误差光谱的最大值hk，若hk

步骤6：计算Sk=2hkwk，βk=(Sk,ck,wk)T。更新β=(β*,βk)，从而代入(2-2)式，使用非线性最小二乘法，对R(v,β)再次进行参数优化，优化参数β*，并更新误差光谱r(v)=Y(v)-R(v,β*)，返回步骤4。