安康地区膨胀土膨胀变形与计算模式
2021-01-29刘宏泰赵佳敏郭敏霞张爱军
刘宏泰,赵佳敏,郭敏霞,张爱军
(1.机械工业勘察设计研究院有限公司,陕西 西安 710048;2.西北农林科技大学 水利与建筑工程学院,陕西 杨陵 712100;3.甘肃省水利水电勘测设计研究院有限责任公司,甘肃 兰州 730000)
1 研究背景
膨胀土是一种具有胀缩性、超固结性、多裂隙性及强度衰减性的特殊黏性土,且膨胀变形具有一定的反复性、潜在性和多发性,会对各类工程产生一定的安全隐患[1-4]。膨胀土在我国分布面积极为广泛,大多分布于南水北调中线及云桂铁路一带[5],且膨胀土通常呈现出连片分布的特点,总计面积已有10×104km2以上。每年发生的膨胀土灾害给全球带来的经济损失已经高达150×108美元以上,学者们普遍称膨胀土为“最难对付的土”[6]。膨胀土对工程产生危害的主要原因是膨胀土自身性质导致的膨胀土胀缩变形,而其膨胀变形程度及膨胀力的大小在本质上是由膨胀土内部吸附水膜的厚度所决定的,合理预估膨胀土在特定条件下的膨胀变形程度,对减少膨胀土地区建筑物破坏具有重要意义。
膨胀土的变形规律需要通过室内、室外试验结合工程实例进行分析,室内试验一般是在有侧限的条件下进行,针对膨胀土的变形研究,很多学者已取得了一系列成果。李进前等[7]研究了不同注水方式对膨胀量的影响,发现开孔与不开孔注水的膨胀时程曲线呈现不同的形式,为膨胀变形率-时间的数学关系建立提供了新思路;高游等[8]基于江苏淮安地区的膨胀土浸水饱和变形试验结果提出了计算最终膨胀量的方法;李佳敏等[9]提出了预测膨胀土无荷膨胀变形的公式,但未考虑上覆荷载的作用,在实际工程中难以运用;张福海等[10]改进了规范中膨胀量的计算方法,并提出了考虑压实度的膨胀土计算模式,具有一定的实用价值;张爱军等[11]提出了同时考虑上覆压力、含水率及干密度的计算公式,更加符合实际情况,但其需进行分段计算,形式不够简单;王亮亮等[12]、杨长青等[13]、池泽成等[14]通过原位平衡加压法对不同地区膨胀土的膨胀力变化规律进行了研究,主要包括不同含水率与干密度的三向膨胀力变化规律及膨胀力-时间变化规律,研究结果能够更为准确地量化膨胀变形。
基于上述研究现状发现,不同地区膨胀土的浸水变形规律会略有不同,因此本文以陕西安康地区的膨胀土(以下简称安康膨胀土)为研究对象,在室内开展不同初始干密度、不同初始含水率下的无荷载膨胀率试验、有荷载膨胀率试验及膨胀力试验,研究不同因素对于安康膨胀土的膨胀变形影响规律。同时为了得到综合考虑初始含水率、初始干重度和上覆荷载3种因素耦合情况下的膨胀土膨胀率变形计算模式,对现有的重塑土膨胀计算公式进行了改进,并用已有的试验数据对该计算模式进行验证,以期为预测膨胀土的膨胀变形及陕西安康膨胀土地区房屋、渠道等工程建设提供参考。
2 试验材料与方法
2.1 试验材料
陕西省安康市属暖温带湿润季风气候,常年雨量充沛,气候温和,四季分明,为丘陵地貌,膨胀土分布广泛。试验用土取自安康机场工程建设现场东南处,取土深度为1.5~7.5 m,土样呈黄褐色。为保证土样含水率等性质不受到扰动,采样后及时采用塑料袋及透明胶带对其密封。
安康膨胀土的基本物理性质如表1所示。根据《土工试验方法标准》(GB/T 50123-2019)[15]可得到安康膨胀土的自由膨胀率为60%,为中膨胀土。为了解安康膨胀土的压实特性,采用轻型击实法得到土样的最大干密度为1.68 g/cm3,最优含水率为22.2%。同时采用日本理学电机公司X射线衍射仪及差热分析等方法对土样的矿物成分进行了分析,结果表明,黏土矿物中含有伊蒙混层、伊利石和高岭石,以伊蒙混层为主;非黏土矿物包括石英、钾长石、斜长石、白云石和赤铁矿,以石英为主(含量为26.7%)。通过土化学分析表明,试样的易溶盐含量均未达到盐渍土的标准,且土中难溶盐含量也较少,表明其与北方膨胀土的性质有所不同,处于南方的安康膨胀土,由于当地雨水的长期浇淋,土样中含盐量很少。

表1 安康膨胀土试验土样的基本物理特性
2.2 试验方法
重塑试样均采用千斤顶静压法制备,将事先粉碎及烘干后的土样过0.5 mm筛,采用喷壶分层喷水以配制含水率分别为12%、15%、18%、21%、24%的试样,用保鲜膜密封保存24 h以上,并用烘干法测其含水率。分别制备5种不同含水率下干密度分别为1.30、1.39、1.47、1.55、1.63 g/cm3的试样,试样直径为61.8 cm,高度为2 cm。试样制备完毕后,利用WZ-1型膨胀仪进行无荷膨胀率试验;利用两联固结仪进行有荷膨胀率及膨胀力试验。有荷膨胀率的荷载等级为0、12.5、50、100 kPa,加压方法为一次加压法,每次压力稳定后从试样底部浸入蒸馏水;有荷膨胀力试验采用平衡加荷法,试验中发现秤砣质量过大,会使试样的压缩变形大于膨胀变形,不能准确量测试样的膨胀力,因此采用烘干的沙代替秤砣施加平衡力,且所有试验均在侧限条件下严格按照《土工试验方法标准》(GB/T 50123-2019)[15]进行。
3 试验结果分析与讨论
3.1 土样无荷载膨胀率试验结果
3.1.1 膨胀变形计算 膨胀土的无荷载膨胀率为土样在无上覆荷载而有侧限情况下浸水产生的垂直变形与土样原始高度之比。本文将试样的竖向膨胀率作为无荷载膨胀率,为同时反映不同初始干密度及初始含水量对无荷载膨胀率的影响,定义容势含水比[11]:
(1)
式中:wr为容势含水比;wm为饱和含水率,%;w0为初始含水率,%。
由于无荷载膨胀率试验的稳定标准是以百分表6 h内读数变化不超过0.01 mm为准,考虑到在试验结束后试样可能还未达到饱和含水率,故将公式(1)中的饱和含水率以试验结束时的含水率替代。对不同初始干密度下的试验结果进行归一化,不同初始干密度及容势含水比土样的无荷载膨胀率试验结果见表2。
容势含水比可以理解为孔隙中还可以容纳水分的能力,它能够更好地表达试样的膨胀潜势,从表2中可以看到,在同一干密度下,含水比越大,土样孔隙中所能容纳水分的能力越强,且该含水比的土样浸水后发生的膨胀变形越明显。将表2中的无荷载膨胀率Vh与容势含水比wr的关系绘制为图1。
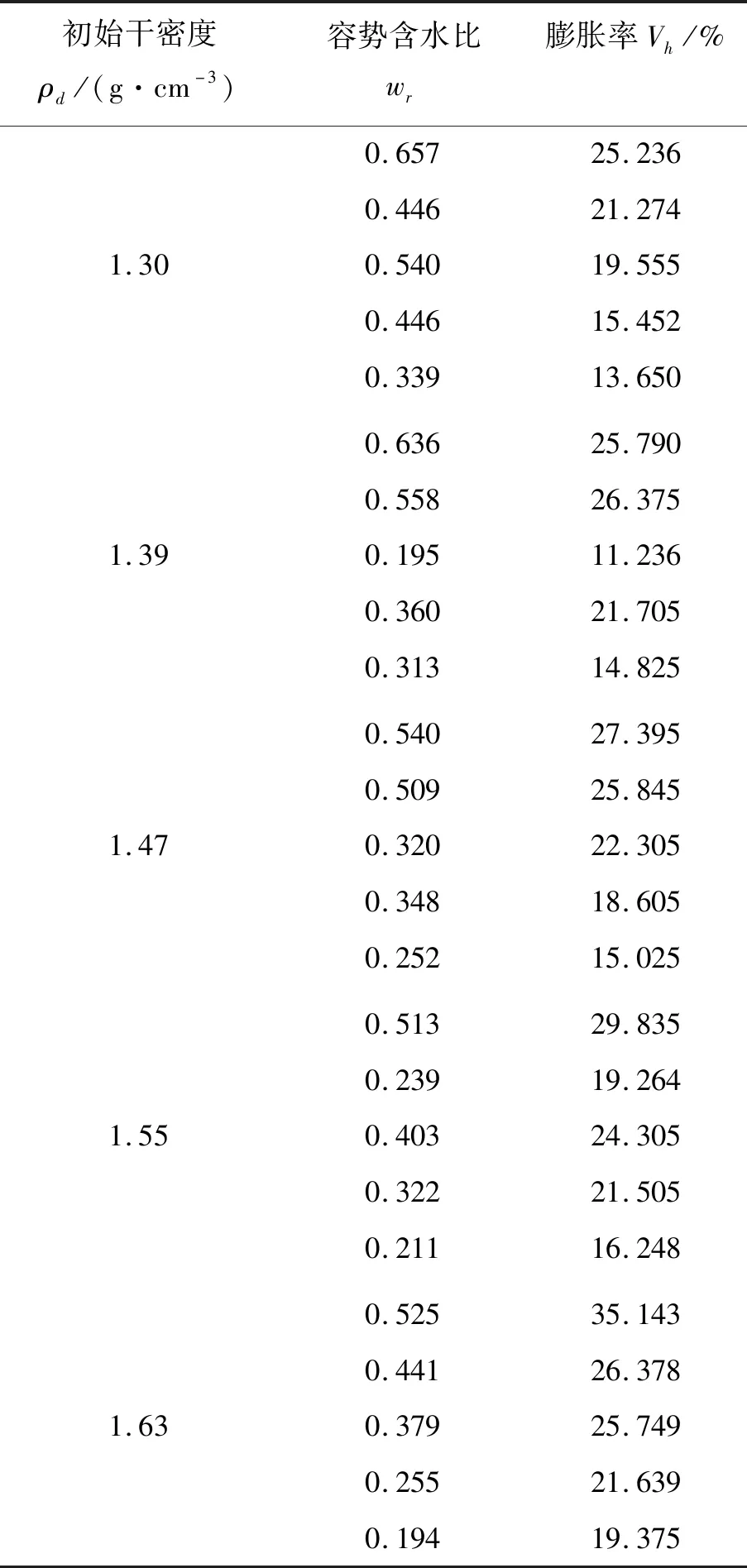
表2 不同初始干密度及容势含水比土样的无荷载膨胀率

图1 不同初始干密度下土样无荷载膨胀率与容势含水比的关系
由图1可以看到,不同初始干密度下土样无荷载膨胀率与容势含水比呈线性关系,可表达为:
Vh=Awr+B
(2)
式中:Vh为无荷载膨胀率;A、B为试验参数。
在同一干密度下,土样无荷载膨胀率随其容势含水比的增大而增大,即随着初始含水率的增大,安康膨胀土的无荷载膨胀率变小。表3为土样不同初始干密度下拟合的试验参数A、B。

表3 不同初始干密度土样的试验参数A、B
将试验参数A、B分别与土样初始干密度ρd进行拟合,其关系曲线如图2、3所示。
从图2、3可以看到,参数A、B均与初始干密度呈线性关系,用直线方程可分别表达为:
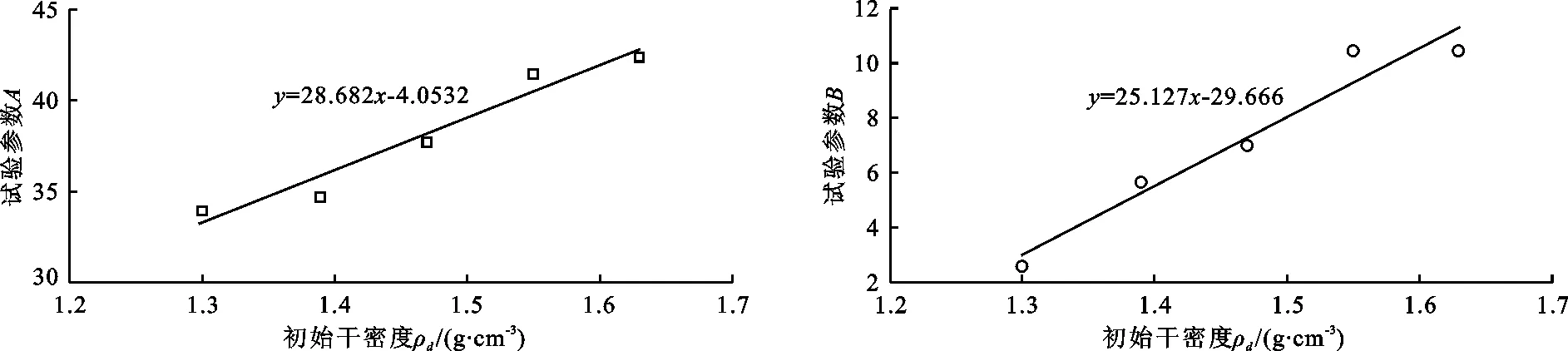
图2 土样初始干密度-参数A关系曲线 图3 土样初始干密度-参数B关系曲线
A=aρd+b
(3)
B=cρd+d
(4)
式中:ρd为土样的初始干密度,g/cm3;a、b、c、d均为试验参数,本文中a=28.682,b=-4.0532,c=25.127,d=-29.666。
将方程式(3)、(4)代入方程式(2)中,可以得到同时考虑初始含水率和初始干密度的土样膨胀变形计算公式:
Vh=(aρd+b)wr+cρd+d
(5)
公式(5)只能计算在含水率和干密度同时作用下土样的无荷载膨胀率,没有考虑上覆荷载的作用。
3.1.2 膨胀变形随时间变化规律 为了得到安康膨胀土浸水后膨胀变形随时间的变化规律,将干密度为1.55 g/cm3土样在不同初始含水率下无荷载膨胀率-时间关系曲线、初始含水率为w0=12%土样在不同初始干密度下无荷载膨胀率-时间关系曲线分别绘制为图4、5。
由图4可以看到,初始含水率对无荷载膨胀率的影响大致分为3个阶段:(1)线性增长阶段:也可称为等速膨胀阶段,此时水初步进入土样并与黏土矿物发生相互作用,使土体急速膨胀,此阶段的膨胀变形占总变形的一半以上,工程中由膨胀变形引起的破坏主要在这一阶段产生;(2)减速膨胀阶段:膨胀速率逐渐变缓,由于土颗粒孔隙间的吸水作用,土样逐渐呈饱和状态,无荷载膨胀率随时间的增长呈现出非线性变化;(3)稳定变形阶段:膨胀率随着时间的增加,基本无变化,且6 h后膨胀变形量各保持在同一水平。
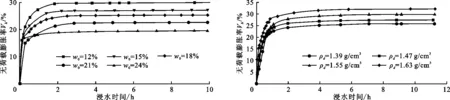
图4 不同初始含水率下土样无荷载膨胀率-时间关系曲线(ρd=1.55 g/cm3) 图5 不同初始干密度下土样无荷载膨胀率-时间关系曲线(w0=12%)
图5反映了干密度对膨胀变形进程的影响。图5中曲线变化形态与上述3个阶段基本相同,但在土样浸水初期,即0~1 h内不同干密度下的曲线间距很小,原因可能是在初浸水阶段,水刚浸入试样表面,由于干密度主要影响土样内部的孔隙分布,而土样表面的孔隙分布相似,所以浸水初期土样的膨胀率很接近;土样的内部结构随着水的浸入而不断调整,在宏观方面即表现为干密度越大则膨胀率越大。将试验数据拟合后,发现Logistic模型可以用来描述安康膨胀土的一维膨胀时程曲线,其常用表达形式为:
(6)
式中:A1、A2、p为模型试验参数;t为时间,h。
通过拟合该模型,发现Logistic模型拟合度均可达到0.99以上。
3.2 土样有荷载膨胀率试验结果
有荷载膨胀率试验是测定土样在一定上覆荷载及有侧限条件下浸水后试样的垂直变形量与原始高度的比值。对不同初始含水率的试样分别进行0、12.5、50、75、100 kPa共5级上覆荷载作用下的膨胀率试验,将不同含水率下有荷载膨胀率Vzp随相对上覆荷载(p+pa)/pa的变化情况绘制为图6(p为所施加的上覆荷载,pa为大气压强,单位均为kPa)。
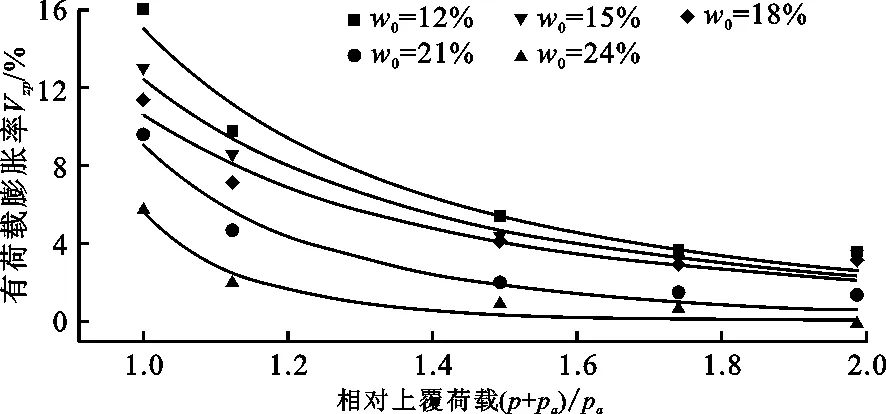
图6 不同初始含水率下土样有荷载膨胀率-相对上覆荷载关系曲线
分析图6可知,上覆荷载对膨胀土的膨胀变形有一定的抑制作用,随着上覆荷载的增大,对土样膨胀变形的抑制作用逐渐加强,且膨胀变形逐渐趋于稳定。具体表现为p=12.5 kPa时,有荷载膨胀率相对无荷载膨胀率减少了64%;p=50 kPa时,有荷载膨胀率相对减少了71%;p=75 kPa时,有荷载膨胀率相对减少了75%;p=100 kPa时,有荷载膨胀率相对减少了76%。这也说明,在实际工程中,为了抑制膨胀土的膨胀变形,可以采取增加外在荷载等措施。
图6中的关系曲线可统一表达为:
(7)
式中:Vzp为有荷载膨胀率;C、D为试验参数;p为所施加的上覆荷载,kPa;pa为大气压强,kPa。
当上覆压力为0时,有荷载膨胀率以参数C表示,其仅与土样的初始含水率和初始干密度相关,且C具有明确的物理意义,即为无荷载膨胀率。结合公式(5)与(7),可构成同时考虑土样含水率、干密度及上覆压力的膨胀土膨胀量计算模式,如公式(8)所示:
(8)
3.3 土样膨胀力试验结果
将不同初始含水率下土样膨胀力-初始干密度关系曲线、不同初始干密度下土样膨胀力-初始含水率关系曲线分别绘制为图7、8。
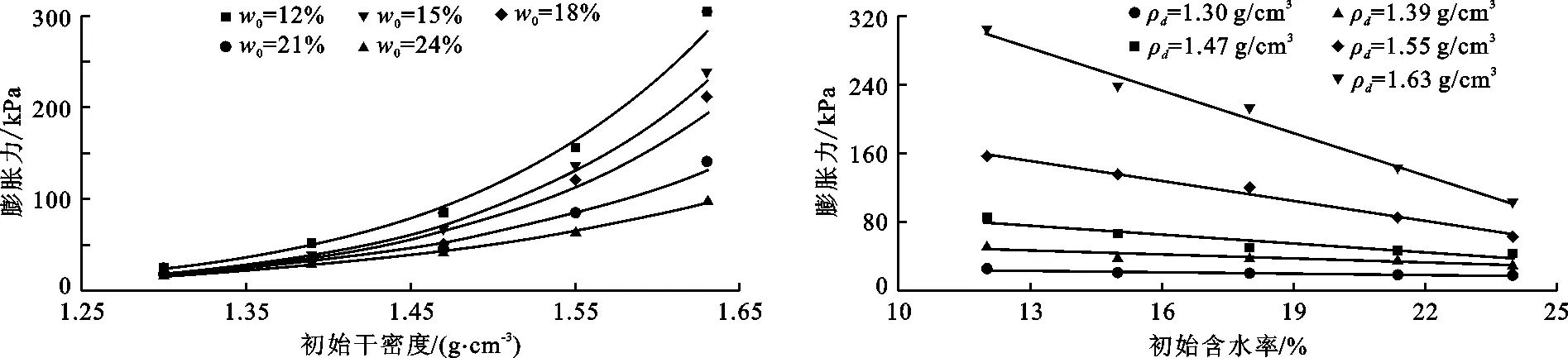
图7 不同初始含水率下土样膨胀力-初始干密度关系曲线 图8 不同初始干密度下土样膨胀力-初始含水率关系曲线
由图7可以看到,土样的初始干密度与膨胀力呈幂函数关系,这与文献[14]中南水北调中端邯郸强膨胀土表现出不同的规律。初始干密度小于1.47 g/cm3时,膨胀力的增加速率缓慢;初始干密度大于1.47 g/cm3时,膨胀力的增加速率显著增大,将1.47 g/cm3视为安康膨胀土干密度的分界点,分界点前后膨胀力与初始干密度均大致呈线性关系。干密度为1.65 g/cm3时的膨胀力相比干密度为1.47 g/cm3时的膨胀力增加了约250 kPa。这是因为在初始含水率相同的情况下,干密度越大的土样内部孔隙分布越紧密,随着水分不断进入膨胀土试样内部,产生的结合水膜的厚度不断增大,会将土颗粒向四周挤压,但由于试样体积保持不变,所以膨胀力逐渐增大。而不同干密度试样的吸水量也不同,在恒体积的情况下,干密度越大,试样中所能容纳的水分越小,这是因为干密度大的土样孔隙相对更少、更小,水分无法进入试样内部[16-17]。
根据图8所示,土样膨胀力与其初始含水率呈明显的线性关系。同一初始含水率(w0=12%)下,干密度为1.63 g/cm3时,土样膨胀力最大,达到300 kPa;干密度为1.30 g/cm3时,土样膨胀力最小,仅有25 kPa。其他含水率下,干密度对膨胀力也产生了相似的影响,将不同初始干密度下土样膨胀力与初始含水率的关系表示为线性方程式(9),5个干密度下的回归关系式见表4。

表4 初始不同干密度下膨胀力与初始含水率的回归关系式
Pz=-Ew+F
(9)
式中:Pz为膨胀力,kPa;w为初始含水率,%;E、F为膨胀力试验中的参数。
方程式(9)中参数E为膨胀力随初始含水率变化的速率,其与土样初始干密度的关系曲线见图9。由图9中可以看出,土样干密度越大,E值越大,即膨胀力随着初始含水率的变化速率越大。当干密度在1.30~1.47 g/cm3之间时,膨胀力随初始含水率的变化较小;而干密度在1.47~1.63 g/cm3之间时,膨胀力随初始含水率的变化明显增大。本次膨胀力试验结果与池泽成等[14]进行的三向膨胀力试验研究中的竖向膨胀力随干密度的变化规律一致。
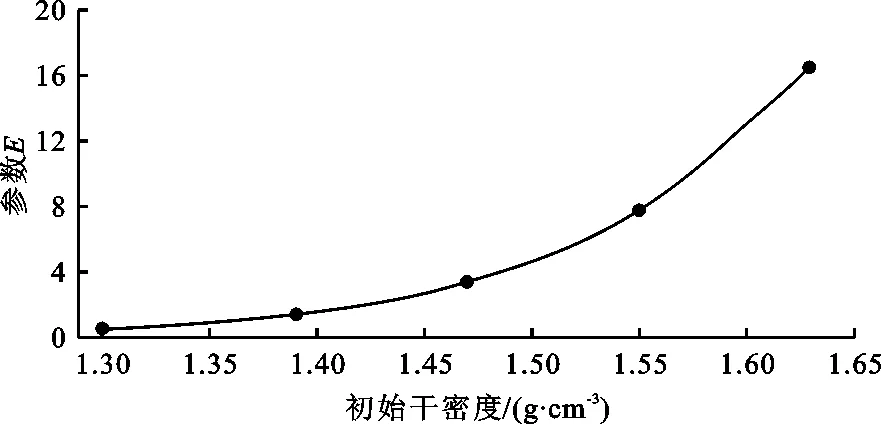
图9 回归表达式中E参数与土样初始干密度的关系
上述试验结果表明,膨胀土的膨胀变形指标可以由膨胀率和膨胀力分别来表征。试样产生膨胀的主要原理是其内部蒙脱石等亲水性矿物吸水导致其内部双电层的不断形成,土颗粒之间的黏结力减小,这一点表现在宏观方面为土体软化,当其不断发展,进而引起土颗粒间的间距增大。当外界条件不同时,土样会产生不同的结果[17]:其一是当允许试样体积发生变化时,土颗粒间距的增加表现在宏观层面即为试样高度的变化,即膨胀率的增大,在这一过程中也伴随着裂隙的产生;其二是当试样体积保持不变时,膨胀潜势会转化为膨胀力的形式作用在外界约束上,可以理解为在有约束的条件下膨胀力才会产生。所以在很多实际工程中,当地基、渠道衬砌等上作用有较大的膨胀力时,地基和衬砌发生变形后会产生应力松弛现象。
4 膨胀率计算模式的验证
试验考虑土样含水率、干密度、上覆荷载3种因素耦合情况下的膨胀率计算模式可以用公式(8)表示。为了验证该计算模式的可行性,用公式(8)对徐永福[18]提出的50 kPa上覆荷载下的膨胀量试验结果进行回归拟合,拟合后的计算公式为公式(10),并将该文献的试验数据与本文计算模式得到的数据进行对比,结果如表5所示。
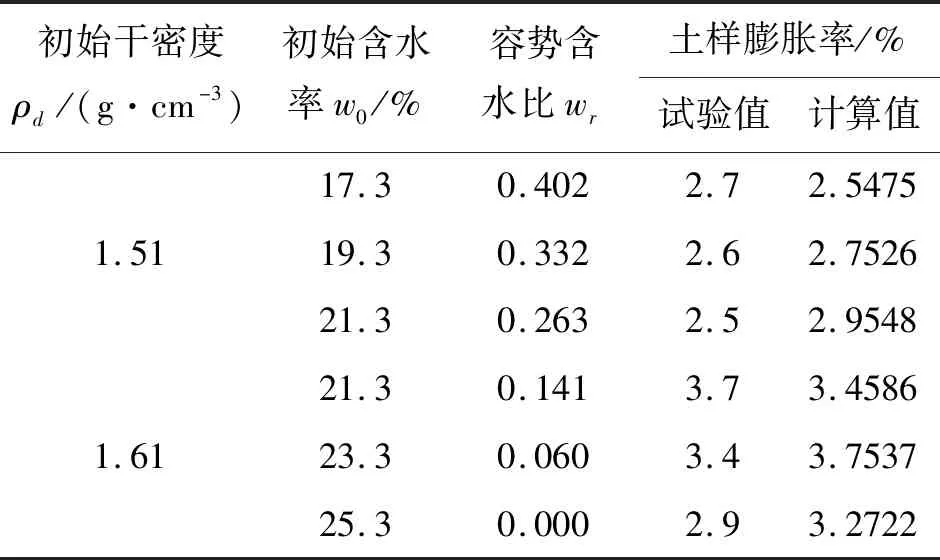
表5 文献[18]土样膨胀率试验结果与本文公式计算结果比较
Vzp=[1.83651ρdwr+6.2395ρd]1.49-2.9587
(10)
由表5可以看出,用本文公式计算出土样膨胀率与试验结果具有一定的误差,但其最大相对误差不超过12.8%,虽个别试验数据具有一定的离散型,但从整体上具有一致性和准确性。说明本文所提出的膨胀率计算模式可以预测膨胀率在含水率、干密度及上覆荷载耦合情况下的变化规律。
5 结 论
(1)一系列土样膨胀率试验结果表明,初始含水率、初始干密度、上覆荷载是影响安康膨胀土膨胀变形的主要因素。无荷载膨胀率随着初始干密度的增大而增大,随着初始含水率的增大而减小。上覆荷载对膨胀变形有抑制作用,且荷载越大其有荷载膨胀率越小。
(2)膨胀力试验结果表明,安康膨胀土的一维膨胀力与初始干密度呈幂函数关系,与初始含水率呈线性关系,且初始干密度越大膨胀力越大,初始含水率越大膨胀力越小。初始干密度大于1.47 g/cm3时,膨胀力受干密度影响更为明显。
(3)通过分析安康膨胀土无荷载膨胀率-时间关系曲线,发现安康膨胀土的膨胀变形随时间的变化趋势可以分为3个阶段,即线性增长阶段、减速膨胀阶段、稳定变形阶段,且它们之间的关系满足Logistic模型,模型拟合度达0.99。
(4)本文提出的安康膨胀土膨胀率计算模式同时考虑了初始干密度、初始含水率以及上覆荷载3种因素,该模式计算结果较为准确,且形式更为简单,具有一定的工程意义和参考价值。
(5)本文所进行的试验均在侧限状态下进行,还可进一步进行三维膨胀变形下的相关试验研究,以更为全面地反映安康膨胀土在实际工程中的变形规律。
