初中数学“教思考”的教学细化
——以“分式”为例
2021-01-29孙朝仁
孙朝仁
“教思考”源于数学教学专家吕传汉等人的研究。他们认为,“教思考”就是在数学课堂教学中,教会学生具备以高层次思维认知客观世界[1];让学生用数学的思维分析世界,学会“想数学”,促进学生思辨能力的培育[2]。这些研究都给了笔者以启发,笔者根据初中数学教学的特点,将“教思考”分解为教学生同化性思考、顺应性思考和迁移性思考,下面以“分式”教学为例详细谈一谈。
一、同化性思考,落细“教思考”学习目标
在生物学研究范畴,“同化”是指生物机体在新陈代谢过程中不发生质变。在数学教育心理学的研究中,同化性思考则是指不改变原有的认知结构,直接将原有的认知经验应用到本质特征相同的一类事物中去,原有的认知结构不发生实质性的改变,只是得到某种充实和丰富。数学教育中的举一反三、闻一知十以及显性变式都是同化性思考的例子。一般来说,概念的获得感主要来自同化性思考,比如“你还能举出具有类似特征的例子吗?”就是同化性思考的一个例子。换句话说,同化性思考是形成问题的思维通道,为概念的发生搭建新旧经验衔接的思维桥梁,进而能让学生获得、感知和判断概念的意义、性质,使得“教思考”的学习目标落地。
基于《义务教育数学课程标准(2011 年版)》(以下简称“2011 年版课标”),教会学生的“数学思考”主要聚焦在三个方面:一方面是在同化性思考中发展学生的形象思维和抽象思维;另一方面是学生在参与观察、实验、猜想、证明、综合实践以及研究性学习活动中,发展合情推理和非完全演绎推理(运算推理)能力,并清晰地表达自己的想法;再一方面是教学生学会独立思考、体会数学的基本思想和基本思维方式。
在“分式”概念教学环节,基于“教思考”的教学需要,根据后续设计的指向与思想题旨可知,确立的学习目标应该是:在具体活动中感受分式概念的意义,知道分式有意义的条件;在探索分式基本性质的过程中,发展逆向思维和模型意识。为此,就“概念发生”目标来说,我们可以创设类似下面的问题组块:
(1)如果一个矩形的长为10 个单位,且面积是60个平方单位,则宽是多少?
(2)如果一个矩形的长为b 个单位,且面积是60个平方单位,则宽是多少?
(3)如果一个矩形的长为b 个单位,且面积是S个平方单位,则宽是多少?
(4)变式1:在(3)的基础上,如果矩形的长增加1个单位长度,面积不变,则宽是多少?
变式2:在上一变式的基础上,如果矩形的长不变,面积减少1个平方单位,则宽是多少?
二、顺应性思考,落地“教思考”学习行为
“顺应”一般指顺从、适应。在数学思考目标研究范畴,顺应性思考是指将原有的认知经验应用于新情境时,需调整原有的经验或对新旧经验加以概括,形成一种能包容新旧经验的更高一级的认知结构,适应外界变化的思维状态。例如,我们为了认识整式的意义,必须先学习单项式和多项式;为了研究分式必须在整式的基础上学习代数式。同时,顺应性思考是数学基本活动经验形成的必经思维桥梁,是概念经验产生式形成的思维结果。换句话说,顺应性结构经验就是学习主体在数学活动过程中,通过感知觉、做与用的操作及反思,获得的具有个性特征的表象性概念、策略性概念以及未经社会性协商的个人概念。日常数学课堂教学中的“会一题、通一类和连一片”就是顺应性思考的一个例子。
2011 年版课标明确指出,通过义务教育阶段的数学学习,学生能获得适应社会生活和进一步发展所必须的数学的基础知识、基本技能、基本思想、基本活动经验。在“教思考”的目标背景下,基础知识主要指向概念与概念关系的建立,例如分式及其基本性质;基本技能则集中指向心智技能的顺应性发展,例如分式的有意义、无意义以及值为零的运算与推理;基本思想聚焦抽象思想、推理思想和模型思想,例如分式基本性质的形成需要用数学的眼光去抽象、数学基本运算去推理、数学的语言去表征等。
在“分式基本性质”概念产生环节,我们可以设置类似下面的问题组块:
(1)如图1,用2 张同样规格的长方形纸片拼成新的长方形。如果一张长方形纸片的面积是S 个平方单位,长为b 个单位,则新长方形的宽是多少?用同样规格的n 张长方形纸片拼成新的长方形纸片,宽是多少?由此,你发现了什么?
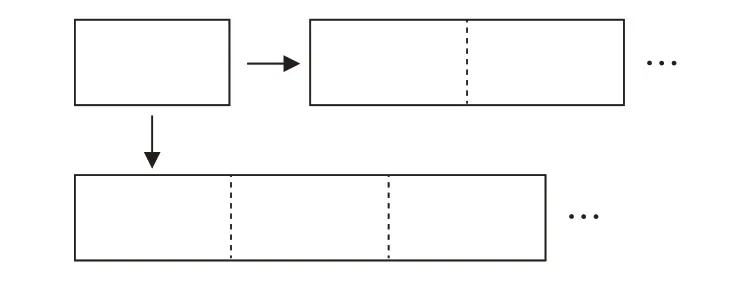
(图1)
(2)如图2,如果将同样规格的1 张长方形纸片沿长边分割成2 等分,则宽是多少?如果将长方形纸片沿长边分割成3 等分、n 等分呢?则宽是多少?由此写出你的发现。

(图2)
(3)经历上述活动,你得到了怎样的数学结论?

三、迁移性思考,落实“教思考”学习表现
马斯洛的“需要层次论”涵盖认知需要、审美需要和自我实现需要,其中“自我实现”是人的最高学习需要。在课堂教学研究范畴,迁移性思考的顶层设计思想就是“自我实现判断”的价值提升,包括系统思维和变量思维的迁移,数学基本思想方法的把握以及概念的关系性理解等。这样的学习层级与发展是知识、能力及其章节概念关系得以综合迁移的内驱行为表现,有助于学生思维导图的联结与架构。平常数学课堂教学中的层次性“小结行为”(先行组织小结、课中概括性小结、课末整合性小结等)都是迁移概念结构的样例,它们有助于学生迁移性思考的发生。当然,迁移并非仅是先前的学习或经验对以后的影响,也包括后面对前面的影响。迁移是指一种学习对另一种学习的影响,或习得的经验对完成其他活动的影响。
同时,迁移不仅存在于某种经验的内部,而且也存在于不同的经验之间,迁移表明各种经验内部及其不同经验之间的相互影响,通过迁移,各种经验得以沟通,经验结构得以整合。这里的“内部经验”可以看作是章节内部概念关系的衔接,比如分式的概念、分式的基本性质以及分式方程之间的章节思维联结关系;而“不同经验之间的关系”可以理解为分数与分式的关联关系、整式与分式的关联关系以及分式方程与一元一次方程、一元二次方程的关联关系等系统思维关系。从2011 年版课标来看,迁移性思考直接指向情感态度价值观目标,也就是“知→情→意→行”思想的高度统一与自我实现价值判断的提升。具体涉及以下迁移:第一是积极参与数学活动,对数学有好奇心和求知欲,也就是问题设置要关注不同学生的参与度与好奇心;第二是在数学学习过程中,体验获得成功的乐趣、体会数学的特点,了解数学的价值,建立数学自信,也就是让学生在具体活动中体验到知识、技能的迁移以及自我实现的满足感;第三是养成独立思考、合作交往、反思质疑的迁移能力以及坚持真理、修正错误的科学态度,也就是让学生在实践中反思总结,在反思中进行经验改造以及系统知识的有序联结。
例如,在“分式”教学的结课环节,我们可以设计如下教学游戏活动:
每人制作几张卡片,在卡片上写一个简单的整式或运算符号:有如“+”“x”“1-x”“x2-1”“-3”“——”“=”等。

毋庸置疑,大数据、区块链、慕课、电子白板、智能教室、翻转课堂、泛在学习等进入课堂,使得数学课堂快速发展。这些现代化学习工具为“教思考”提供了便捷的认知桥梁和变量方法,有助于不同学力的学生达到数学教育教学目标,形成“关键能力”和“必备品格”。
