聚焦增值,让数学复习课温故知新
——以苏教版五上《多边形面积计算的复习》的教学为例
2021-01-29王海峰
王海峰
提起数学复习课,不少教师脑海中会浮现出这样的场景:老师在台上讲得声情并茂、声嘶力竭;学生在台下学得无精打采、无动于衷。复习课上习题一道道、试卷一张张,但最后的结果往往是:一堂课下来,学生原本会的还会,原本不会的还不会,复习课只是例行公事、走走过场般的“炒冷饭”。上述现象或许并非普遍存在,但复习课收效甚微的问题确实成为不少教师心中的痛。
华东师范大学崔允漷教授认为,学习有四种值:一是动力值,即学生想学习的愿望;二是方法值,即学生会学习的方法;三是知能值,即学生所学到的知识与技能;四是意义值,即学生学到的东西是有意义或受用的。他还说,必须至少有一种值增加(即学后值与学前值之差为正量),没有增值的课堂没有意义。笔者深表赞同,没有增值的课堂就是在浪费学生的时间和生命。进一步讲,不只是新授课要实现至少一种值的增加(新授课要实现增值可以说轻而易举),复习课也应如此。下面,笔者以苏教版五上《多边形面积计算的复习》的教学为例,谈谈如何聚焦课堂增值,让复习课“炒冷饭”的现象得以改变,真正做到温故知新。
一、开门见山对话,让学生既明目标又悟价值,实现意义值的增值
复习课是数学教学中一种常见且重要的课型,上好复习课,对于学生夯实所学知识点,将知识点系统化、结构化,提升思维品质,发展数学素养起着至关重要的作用。但学生对复习课的意义与价值未必了解,甚至可能从来就没思考过这样的问题,只是按部就班地完成教师在复习课上布置的一个又一个任务,学习热情不高带来的结果就是学习效果不理想。因此,本节课伊始,教师和学生有了如下的对话。
师:今天这节课,我们一起来复习多边形的面积计算。(板书课题:多边形面积计算的复习)同学们想一想,复习课和我们平时上的新课有什么不同?
生:复习课讲的都是我们已经学过的知识,新课讲的都是我们没有学过的知识。
师:既然都已经学过了,大家都会了,为什么还要上复习课呢?
生1:复习课可以让我们对原来学过的知识加深印象,这样做题目更熟练。
生2:复习课可以让我们对一个单元学的知识理解得更清楚,尤其是前后几个知识点之间的联系。
生3:孔子说“温故而知新”,我觉得复习课可以让我们通过复习学到新的知识。
师:同学们说得真好!下面就让我们一起来边温故边知新。(板书:温故而知新)
复习课与新授课有什么不同?课始,教师把这个问题抛给学生,“逼迫”学生在复习课的开端就思考这一本源性问题,大家在交流碰撞中逐步明晰复习课的意义与价值。开门见山式的访谈直抵学生内心,促进他们思考“要不要学”“想不想学”,让学生在内省的过程中实现复习课意义值的增值。
二、自主操作交流,让学生既知结论又懂过程,实现知能值的增值
学习了几种多边形的面积计算公式之后,学生在平时的练习中遇到更多的是运用公式解决面积计算的实际问题,而对面积计算公式是如何得到的往往会忽略、淡忘。只有知其所以然,才能更长久地知其然。因此,在课的前半部分,教师要让学生充分操作、交流,让原先对公式掌握不熟练的学生熟练掌握公式(结论),让原先对公式推导过程淡忘的学生进一步理解推导过程,使每一位学生在原有基础上实现知能值的增值。
师:我们已经学会了计算哪些多边形的面积?(根据学生的回答,出示长方形、正方形、平行四边形、三角形、梯形)给出这些多边形的数据,你会计算它们的面积吗?(课件出示标有字母数据的几种多边形)
师:刚才大家所说的其实就是多边形的面积计算公式。(根据学生的回答,在黑板上贴出多边形,上面写其面积计算字母公式)
师:回忆出面积计算公式是什么,是我们今天复习的初级水平,我们还要想想这些公式是怎么得到的。老师给每个小组准备了一个信封,里面有各种多边形纸片,请前后四人一组,每人选择一到两种,在小组内说说这个图形的面积计算公式是如何推导出来的。可以在图形上画一画、写一写,也可以剪一剪、拼一拼。
师:在打开信封之前,我先问一问大家,你希望信封里每种多边形各有几个?
生:我希望长方形纸片、正方形纸片和平行四边形纸片可以只有一个,但三角形纸片、梯形纸片能有两个,而且两个完全相同。
师:其他同学也是这么想的吗?老师还真给大部分小组都准备了两个完全一样的三角形纸片和梯形纸片,但有少数小组老师可能一时疏忽,只准备了一个三角形纸片和一个梯形纸片,如果哪个小组拿到只有一个的,你们就中奖了,老师也对你们提出更高的要求了——能不能只用一个三角形纸片或者一个梯形纸片,就推导出它们的面积计算公式?
学生小组活动,探索、交流多边形面积的推导过程。
本环节,教师为学生准备好探索面积计算公式所需的学具,让学生充分画、剪、拼、说,把书本上静态的结论性公式变成动态的获得公式的过程。学生在自主操作交流的过程中,对每个计算公式理解得更为透彻。教师在本环节特意设置了三角形纸片、梯形纸片个数不足的障碍,为学生后续更深入的探讨埋下伏笔。
三、“花式”推导验证,让学生既开眼界又促思考,实现方法值的增值
关于多边形的面积计算,经过两个阶段的学习和练习,学生似乎对此已经司空见惯,没有新的疑问和惊奇,其实不然。在复习了每个公式的常规推导过程之后,教师寻找学生已有知识经验的生长点,借助前面设置的多边形纸片个数的障碍,“逼迫”学生思考三角形与梯形不同的面积推导方法,让学生在“花式”推导验证的过程中开阔眼界、拓宽思路、促进思维,从而实现学习方法值的增值。
师:刚刚有的小组只拿到了一个三角形纸片和一个梯形纸片,用一个三角形纸片和一个梯形纸片能推导出三角形、梯形的面积计算公式吗?请其他小组也在组内讨论思考这个问题。
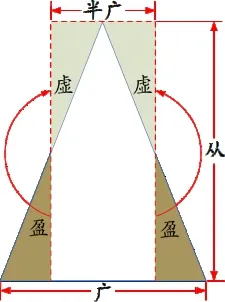
生1(边演示边交流):我在书上“你知道吗”看到过用一个三角形推导三角形面积计算公式的方法。将三角形从一条边的中点向下作高、剪下,旋转拼到上面,另一边也这样操作,就可以把三角形转化成长方形,三角形的底的一半是长方形的宽,三角形的高是长方形的长,所以三角形的面积=底×高÷2。
师:讲得真好,这就是《九章算术》中“半广以乘正从”的方法。(课件出示推导图,如图1)还有不同的推导方法吗?
生2(边演示边交流,如图2):将三角形沿两条边的中点剪下,旋转拼到下面,可以将三角形转化成平行四边形。三角形的底等于平行四边形的底,三角形的高等于平行四边形高的一半,所以三角形的面积=底×高÷2。
(图1)
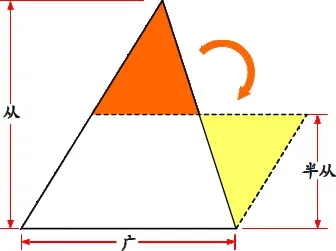
(图2)
生3:这种方法也可以用一句话来概括——“正广以乘半从”。(教室里掌声雷动)
师:同学们的创意出乎我的意料!但我还不满足,你们能用一个梯形推导出它的面积计算公式吗?
生1:可以连接梯形的对角线,将梯形分成两个三角形。一个三角形的面积是上底乘高除以2,另一个三角形的面积是下底乘高除以2,梯形的面积=上底×高÷2+下底×高÷2=(上底+下底)×高÷2。
师:真好!把梯形转化成三角形,也能推导出它的面积计算公式。
生2:其实,也可以仿照刚才推导三角形面积计算公式的过程,把梯形转化成长方形或平行四边形,推导出梯形的面积计算公式。
师:想法太棒了,课上时间有限,课后大家可以用这个思路试一试。
复习课也应努力寻找学生思维水平发展的新生长点,不断给学生创造锤炼思维、提升素养的机会,让学生在思维挑战中获得更好的发展。在设计这节课时,笔者的初衷是给学生创造更多思维创新的机会,没想到在实际教学过程中,学生还真把三角形、梯形面积推导的多种方法创造出来了。课件中预先做好的用于启发学生思维的推导过程图,成为学生推导成功后的总结概括图。
四、多维沟通联系,让学生既见树木又见森林,实现动力值的增值
由于课时划分等原因,在日常新授课的学习过程中,学生学到的知识往往是孤立的、零碎的,对于各知识点之间联系的体会不深刻,难以从整体上结构化地理解知识块。复习课恰恰可以帮助学生沟通知识点之间的联系,让学生既见树木(各个知识点),又见森林(整体知识块)。当学生对所学的知识点从更高维度有了更透彻的理解之后,一定会在很大程度上激发起他们的学习热情,从而实现学习动力值的增值。
师:从刚才大家交流这些公式的推导过程中,我们可以发现,这些公式之间有内在联系。你能根据公式之间的联系,调整一下黑板上这五个多边形的位置,用箭头连一连,让人一眼就能看出五个面积计算公式之间的关系吗?
学生的反馈如下图3~图5所示。
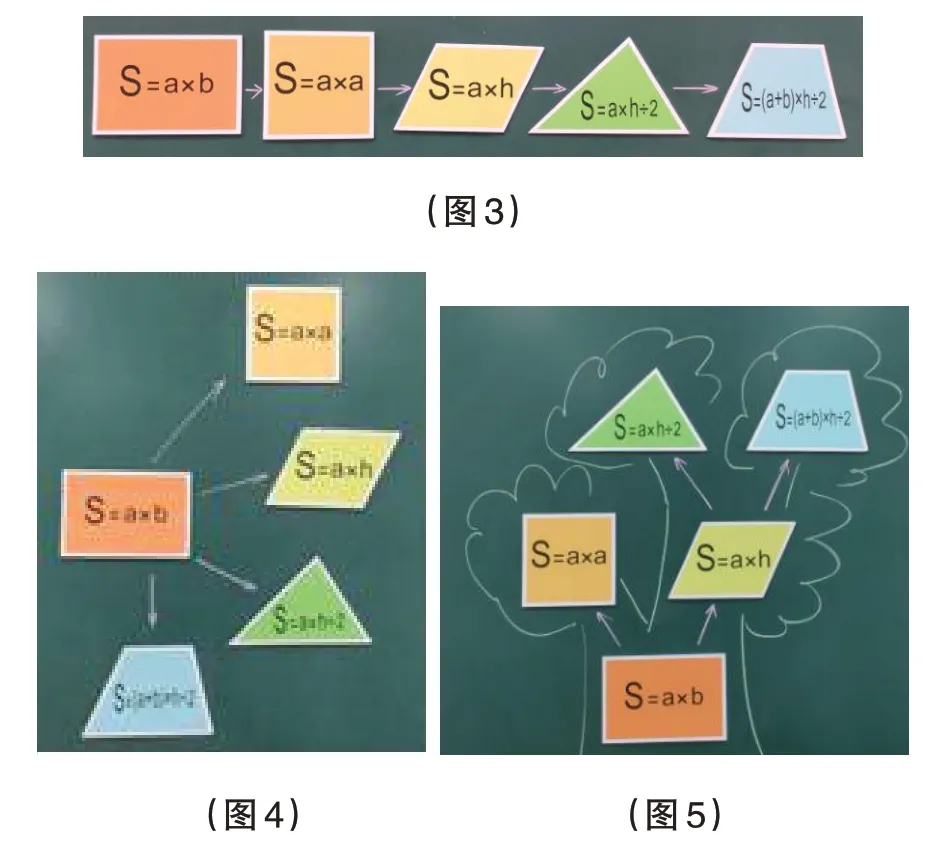
师:大家看,我们在研究正方形、平行四边形、三角形、梯形的面积计算公式时,都是把新问题转化为旧问题。转化是数学学习中非常重要的思想方法。(板书:转化)
在弄清几种多边形面积计算公式之间的关系之后,教师继续乘胜追击。
师:这些公式中,你觉得哪个公式最复杂?
生(异口同声):梯形面积计算公式最复杂。
师:其实,这个最复杂的公式也可以用来计算其他多边形的面积。
师(课件出示将梯形上底逐渐延长变成长方形的过程):如果把现在这个长方形还看作梯形,梯形上底是多少?下底呢?用梯形面积计算公式计算这个长方形的面积,与用长方形面积计算公式计算得到的结果一样吗?
师(课件出示梯形上底不断缩短直至变成三角形的过程):如果把这个三角形还看作梯形,梯形的上底变成了多少?用梯形面积计算公式计算这个三角形的面积,你有什么发现?
…………
课末,教师带领学生交流本节复习课的收获之后,教师在学生现有知识框架之上再次抛出新问题:普通四边形的面积如何计算?为什么后面不再学习五边形、六边形等其他多边形的面积计算公式?
无论是让学生摆多边形的面积计算结构图,还是引导他们尝试用最复杂(最一般)的梯形面积计算公式去计算其他多边形的面积,抑或是课的最后启发学生思考“为什么学完这五种多边形的面积计算之后,教材不再安排学习其他多边形的面积计算(进一步强化转化的思想)”,都旨在让学生的视线跳出一个个单体的多边形,站到更宏观的视角对所学知识进行系统的观察和定位,用联系的视角建构起多边形面积计算的知识体系。在多维沟通联系的过程中,学生的眼界更加高远,思维更加通透,学习的热情也随之升华,从而实现学习动力值的增值。
正如冯卫东先生所说:为“真学”而教,也为学生获得而教;如果不为获得,还要教与学做什么。学生有获得,能增值,他的学习则是成长性学习。数学复习课就应该以这样的理念为指导,勇于向司空见惯的复习课“炒冷饭”说不,重视夯实每个知识点,重视将知识点串成知识链、织成知识网,立足儿童立场,聚焦儿童增值,让每一位儿童都能在复习课上有所得。
