云南松单木材积生长率模型研究
2021-01-28魏安超张大为
魏安超,张大为
(1.云南金杉工程建设监理咨询有限公司,昆明 650051;2.国家林业和草原局调查规划设计院,北京 100714)
材积生长率是树木生长过程中,某间隔期材积生长的相对速度,它是测定材积生长量的主要指标,是更新年度森林资源数据的主要依据[1]。国外许多林业发达国家在18世纪就有了对森林生长量和收获的相关研究[2-3],之后便出现针对森林生长模型的研究,在此基础上,许多国家在建立森林资源连续监测固定样地的同时,提出了适合本国的森林生长模型,其中就包括材积生长率模型[4-5]。国内学者黄中立[6]较早从单株树木生长量、单位面积树木共同生长量和生长率3个方面对我国杉木(Cunninghamialanceolata)材积生长率等问题进行了研究;曾伟生等[7-8]利用一类清查固定样地资料对湖南和西藏的马尾松(Pinusmassoniana)和杉木材积生长率模型进行了研究,提出了二元材积生长率标准动态模型;沈家智等[9]用一类清查数据中的1 320株湿地松(Pinuselliottii)复测样木数据,建立了以胸径和年龄为变量的二元材积生长率动态模型;程光明[10]用逐步回归方法建立了可变参数的材积生长率模型;廖志云等[11]在建立了不同树种的胸径生长率模型的基础上,推导出相应树种的材积生长率模型;甘世书[12]编制了海南省松树(Pinus)和橡胶树(Heveabrasiliensis)的单木和林分材积生长率模型,拟合精度较高。
云南松(Pinusyunnanensis)是我国西南部干性亚热带区域重要的建群种,其林分面积占云南省林地面积的比重大,是云南山地更新造林的先锋树种。前人已对云南松林的径级结构[13]、种群更新[14]、空间结构[15]、生长过程和生长模型[16]等方面进行了广泛研究,但对其单木生长率尤其是材积生长率的研究则鲜见报道。涉及材积生长率模型的影响因子一般包括年龄、胸径、树高和森林经营管理活动[17]等,本文基于云南省第六次和第七次森林资源连续清查数据,以滇中地区云南松为研究对象,以与林木材积生长率大小密切相关的海拔、起源、龄组和林分密度为指标,分别建立滇中地区云南松单木材积生长率模型,旨在为云南松林资源的可持续经营提供经验模型。
1 研究区概况
滇中地区位于云南省中部,总面积约9.5 万 km2,约占全省总面积的24%,包括昆明、曲靖、楚雄和玉溪4个地级市。地处云贵高原与横断山脉交界处,属高原盆地,地形多以山地和山间盆地为主,地势南低、北高,起伏和缓。位于红河、珠江及长江上游,有滇池、抚仙湖及阳宗海等高原湖泊,水资源充沛。滇中地区属低纬度亚热带高原季风气候,日照充足,气候宜人,年均气温14.8~23.8℃之间,气候温暖,四季温差不大。区内降水干湿季分明,降水主要集中在5—9月,年均降雨量约 800mm。地形以山地和山间盆地为主,喀斯特地形地貌在滇中地区分布较广泛,使得地表下渗严重,土壤层较薄,整体涵养水源能力较差。地势起伏较大,该地区海拔最高4 344m,最低695m,海拔高差达3 649m。
2 研究方法
2.1 数据来源及处理
采用的基础数据来源于云南省第六次(2002年)和第七次(2007年)森林资源连续清查(一类调查)结果。筛选滇中地区优势树种为云南松且样地号连续的数据,共373块样地、11 283株样木。云南省森林资源连续清查采用系统抽样方法,抽样间距为6km×8km,现地设置方形实测样地,样地面积0.067hm2,调查内容包括了样地因子和样木因子的各项特征资料。
2.2 梯度划分
1) 云南松所处生境的海拔区间为910~3 070m,结合前人研究成果,根据滇中地区云南松分布特征将海拔梯度划分为4个梯度,即:海拔<1 500m;1 500m≤海拔<2 000m;2 000m≤海拔<2 500m;海拔≥2 500m。各海拔梯度下的样地数分别为28,139,184和22个,对应样木分别为501,4 147,5 709和926株。
2) 根据森林资源连续清查技术规定,划分起源和龄组,分别为天然林和人工林,对应352和21个样地以及10 201和1 082株。幼龄林(156个样地)、中龄林(118个样地)、近熟林(71个样地)、成熟林(24个样地)、过熟林(4个样地);各龄组对应的样木分别为4 907,4 067,1 906,388和15株。
3) 根据林分密度指数(SDI)划分4个密度等级,即:SDI<1 000为Ⅰ密度级(136个样地);1 000≤SDI<2 000为Ⅱ密度级(123个样地);2 000≤SDI<3 000为Ⅲ密度级(50个样地);SDI≥3 000为Ⅳ密度级(64个样地)。各密度级对应样木分别为2 822,3 990,2 589和1 882株。
按不同指标的梯度划分标准,首先计算云南松单木材积生长率;再将样本数据按1cm进行径阶整化,求算各径阶单木材积平均生长率;随机选取各梯度数据中的75%作为建模数据,其余25%作为模型检验数据。
2.3 林分密度指数(SDI)计算
林分密度指数(SDI)是评定林分内树木间拥挤程度的指标,是现实林分株树换算到标准平均直径时所具有的单位面积林木株数[18]。其计算公式如下:
(1)
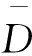
2.4 单木材积生长率计算
将前后两期数据进行连整合,以前期胸径为自变量,按普雷斯勒公式(2)计算云南松单木材积生长率作为因变量。
(2)
式中:Pv为材积生长率(%);Vb为期末样木测定材积(m3);Va为期初样木测定材积(m3);n为复测间隔期(5年)。
2.5 单木材积生长率模型的选择
结合国内外材积生长率的研究成果,选用4种常用的材积生长率模型表1。

表1 材积生长率模型
2.6 单木材积生长率模型拟合和精度检验
采用决定系数(R2)和均方根误差(RMSE)为选取最优模型的参考指标,再根据精度检验要求,通过总相对误差(RS)、平均相对误差(EE)、绝对平均相对误差(RMA)和预估精度(P)对模型偏差统计量进行比较,评价模型的预测能力[21]。
1) 总体相对误差(RS)
2) 平均相对误差(EE)
3) 绝对平均相对误差(RMA)
4) 预估精度(P)
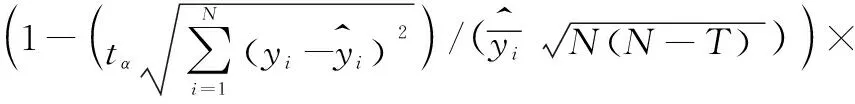
100%
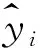
3 结果与分析
3.1 不同海拔生长率模型拟合及精度检验
对不同海拔下云南松单木材积生长率模型进行拟合及最优模型精度检验的结果如表2所示。以模型3为最优模型形式,决定系数R2分别达到了0.940,0.936,0.932,0.810,均方根误差RMSE分别为1.180,0.981,1.689,1.894。具体模型形式分别为:y=55.498×D(-0.517)-7.087;y=50.194×D(-0.647)-2.914;y=41.299×D(-0.291)-12.149;y=21.165×D(-0.310)-4.004。
由检验结果来看,最优模型的预估精度均在80%以上,当海拔处于1 500~2 000m时最高,达到了93.561%,在低于1 500m时最低,仅81.984%。总相对误差在±10%以内,满足林业生产实践的精度要求。综合来看,建模效果和检验结果比较理想,模型适应性较强。

表2 不同海拔云南松单木材积生长率模型拟合及最优模型精度检验
3.2 不同起源生长率模型拟合及精度检验
对不同起源下云南松单木材积生长率模型进行拟合及最优模型精度检验的结果如表3所示。天然林的决定系数R2最高及均方根误差RMSE最小的为模型2,分别为0.947和1.949,人工林的决定系数R2最高及均方根误差RMSE最小的为模型3,分别为0.899和2.031。故具体模型形式分别为:y=16.984×0.938D+0.847;y=60.983×D(-1.112)+1.713。
由精度检验结果来看,云南松天然林和人工林单木材积生长率模型拟合的最优模型检验精度分别为91.983%和86.641%,总体相对误差在±6%以内,建模效果和检验结果比较理想,且满足林业生产实践精度要求,故选出模型适应性强。
3.3 不同林分密度生长率模型拟合及精度检验
对不同林分密度下单木材积生长率模型进行模拟及最优模型精度检验的结果如表4所示。模型3为Ⅰ密度级和Ⅱ密度级的最优模型,决定系数R2分别为0.979和0.981,均方根误差RMSE分别为0.782和0.817;模型2为Ⅲ密度级和Ⅳ密度级的最优模型,决定系数R2分别为0.952和0.858,均方根误差RMSE分别为0.679和1.264。因此,4个林分密度级的最优单木材积生长率模型形式分别为:y=60.651×D(-0.350)-16.91;y=47.653×D(-0.269)-16.978;y=14.653×0.96D-0.657;y=70.685×0.997D-62.986。
由模型精度检验结果来看,不同林分密度下云南松单木材积生长率模型拟合的最优模型检验精度均达到89%以上,总体相对误差在±10%以内,模型模拟和检验结果良好,满足林业生产时间的精度要求。

表3 不同起源云南松单木材积生长率模型拟合及最优模型精度检验

表4 不同林分密度云南松单木材积生长率模型拟合及最优模型精度检验
3.4 不同龄组生长率模型拟合及精度检验
对不同龄组单木材积生长率模型进行模拟及最优模型精度检验的结果如表5所示。各龄组均以模型3为最优模型形式,决定系数R2分别达到了0.968,0.930,0.934,0.928和0.959,均方根误差RMSE分别为1.532,0.986,0.886,1.458和1.697。具体模型形式分别为:y=51.965×D(-0.241)-17.163;y=48.685×D(-0.155)-23.653;y=59.983×D(-9.853)+0.924;y=123.653×D(-1.127)-0.649;y=467.353×D(-1.521)-1.239;
由模型精度检验结果来看,成熟林和过熟林的最优模型拟合决定系数R2均大于0.92,但预估精度分别为80.685%和70.619%,可能是因为模型拟合和检验的样木数据量少,模型预估精度较小。除此之外,其余龄组模型预估精度均大于90%,且总体相对误差在±15%以内,满足林业生产时间时的精度要求,所选模型具有较强的适应性。

表5 不同龄组云南松单木材积生长率模型拟合及最优模型精度检验
4 结论与讨论
4.1 结论
1) 云南松单木材积生长率随胸径增加而减小,这也意味着随树龄的增加而减小。在胸径增大的同时样木株数减少,故在大径阶时,材积生长率稍有起伏但趋于平稳。整体呈反“J”型曲线分布,即该地区云南松多属幼龄林、小径木,这也与骆期邦等[22]、姜磊等[13]的研究结果相符。
2) 通过比较分析拟合的云南松单木材积生长率模型,模型1的拟合效果和精度相对不高,模型3表现整体最优。其中不同海拔梯度下的最优模型分别为:y=55.498×D(-0.517)-7.087;y=50.194×D(-0.647)-2.914;y=41.299×D(-0.291)-12.149;y=21.165×D(-0.310)-4.004。天然林和人工林的最优单木材积生长率模型分别为:y=16.984×0.938D+0.847;y=60.983×D(-1.112)+1.713。4个林分密度级最优单木材积生长率模型分别为:y=60.651×D(-0.350)-16.91;y=47.653×D(-0.269)-16.978;y=14.653×0.96D-0.657;y=70.685×0.997D-62.986。5个龄组最优单木材积生长率模型分别为:y=51.965×D(-0.241)-17.163;y=48.685×D(-0.155)-23.653;y=59.983×D(-9.853)+0.924;y=123.653×D(-1.127)-0.649;y=467.353×D(-1.521)-1.239。经适用性模型精度检验,最优模型R2大于0.8,可用于云南松材积生长量的估算、编制材积生长率表及对未来云南松林分资源的动态变化进行预测,在森林资源调查中亦具有一定参考价值。
4.2 讨论
本研究采用森林资源连续清查数据中的前后两期复测样地资料,对大尺度区域下的云南松单木材积生长率模型进行了模拟,从连续清查数据中筛选的样地和样木数据量大,具有很强的代表性,模型精度检验也取得了较好的结果。从结果可以看出,目前滇中地区云南松林分结构存在不合理现象,幼龄林过多,成熟林相对较少,应及时调整林分内各径阶的株树分布,使其生长率进一步提高。但研究中未模拟云南松林分材积生长率生长模型,也未考虑前后两期之间存在的森林经营管理活动,如抚育间伐、疏伐等较强的人为活动对材积生长率的影响,未根据胸径所对应的材积生长率进行编制材积生长率表,在今后的研究中有待于进一步加强。
