从理论角度降低低本底α、β测量仪净计数率探测下限研究

金 涛，孙 宇，张志鹏，吴 耀，宋纪高，李俊杰，罗远攀，裴 敏，曾 波

(中国核动力研究设计院四川省退役治理工程实验室，成都 610005)

核设施流出物及环境监测经常涉及某一介质中总放射性测量或者某一介质中某一核素活度浓度测量，经常要用到低本底α、β测量仪，由于低本底α、β测量仪具有一定本底计数率，因而存在探测下限，当净计数率低于探测下限时，则认为样品没有放射性。由于探测下限的限制，阻碍我们对更低水平放射性活度浓度的测量，为此本文从理论出发对低本底α、β测量仪探测下限的计算公式进行了优化。

判断限和探测限的概念最早由Curie[1]于1968年提出，并通过假设计数服从泊松分布和高斯分布的情况下推导净计数形式的探测限LD：

(1)

式中，NB为本底计数。

1986年Brodsky[2]在本底计数近乎为0的情况下将公式(1)中2.71修正为3，该公式即使准确也存在局限性(即本底计数近乎为0)，事实上该公式存在问题，即：当本底计数近乎为0的情况下，判断限LC为一个大于0小于1的很小的数，则小于判断限LC的总计数只能为0，假设总计数服从泊松分布，则总计数的平均值为3时，总计数率的随机数低于判断限(即总计数等于0)的概率为e-3，接近0.05。但当总计数平均值为3的情况下，易知总计数是不符合泊松分布，该修正是存在一定问题的。1999年国际原子能机构(IAEA)发布RSG 1.2报告[3]，报告中推荐的探测下限公式如下：

(2)

式中，LD为活度形式的探测下限，Bq；F为探测效率、回收率相关的转换因子；nb为本底计数率，cps；ts为样品测量时间，s；tB为本底测量时间，s。2000年国际标准化组织(ISO)发布ISO 11929.1标准[4]，该标准给出的计数率形式的探测下限如下：

(3)

式中，LD为探测限，cpm；ts为样品测量时间，min；tb为本底测量时间，min；ρb为本底计数率，cpm；k1-α为分位数，k1-β为分位数。

Strom、Rigaud[5-6]分别于2001年和2003年开展研究，证明公式(1)和公式(2)存在一定缺陷，不能很好地应用。2004 年美国发布的NUREG-1576报告[7]给出了计数形式的探测下限公式：

(4)

(3)式给出的计数率形式的探测下限公式，方程两边乘以ts，很容易得到计数形式的探测下限，即(4)式。

吴志华等[8]在《原子核物理实验方法》一书中给出探测下限公式，与Curie给出的探测下限公式大同小异，具体如下：

(5)

当k=1.645时，(5)式与Curie推导的(1)式一样。

2006年国防科技工业委员会发布了EJ/T 1204.1《电离辐射测量探测限和判断阈的确定 第一部分：忽略样品处理影响的计数测量》[9]，该标准给出的探测下限的公式与ISO 11929.1标准完全一致。

2013年韩学垒[10]在《环境放射性监测中的探测下限及优化探讨》一文中给出了低本底测量环境下的计数率形式的探测下限公式，与(2)式在参数上略有差异，基本形式相同：

(6)

国内外给出的探测下限公式并没有统一，下面给出一种新的净计数率形式的探测下限公式及其推导过程，并对该式和上文的(3)式进行修正，并给出修正系数。

1 推导过程

1.1 判断阈

根据统计假设检验的方法，我们首先可以假设样品是否具有放射性，比如：

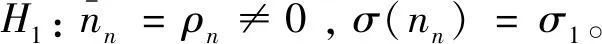
容易知道随机数nn近似满足正态分布，那么统计量(nn-ρn)/σ1近似满足标准正态分布。我们先认为假设H0是成立的，也就是说样品没有放射性。根据分位数的定义，如图1所示，服从标准正态分布的随机变量(nn-ρn)/σ1大于kα的概率为α值，α是一个很小的数，比如0.05、0.025等等，根据“小概率事件在一次试验中几乎不可能发生”的原则，如果统计量(nn-ρn)/σ1在一次实验中大于kα，那么原假设H0不成立，选择被择假设，则认为样品具有放射性。这就是说当统计量nn大于LC=kασ1，样品认为是有放射性的。否则，认为样品没有放射性，因此将LC成为判断限。换句话说，当净计数率nn大于判断限，则认为样品具有放射性，否则认为没有放射性。

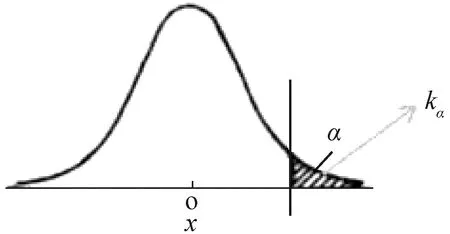
图1 k分位数Fig.1 k Quantile

1.2 探测下限

另外，我们可以先假设样品具有放射性，例如：

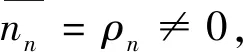
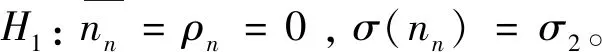
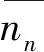
根据判断阈的定义，如果某次试验中随机数nn小于判断阈LC，则样品没有放射性。此时定义“nn小于判断阈LC”为一个新的事件。当“nn小于判断阈LC”事件发生的的概率小于或等于一个小概率值β值时，根据“小概率事件在一次试验中几乎不可能发生”的原则，可以判定样品具有放射性。也就是说如果满足公式(7)，则样品具有放射性。但是这种判断是可能犯第二类错误的，而犯第二类错误的概率应小于等于小概率值β值。公式(8)与公式(9)等价于公式(7)：

(7)

(8)

ρn≥LC+kβσ2=kασ1+kβσ2

(9)

1.3 推导过程

在正常情况下，本底是未知的，为方便起见，假设Nn为净计数，Ns为样品计数，Nb为本底计数，nn为净计数率，ns为样品计数率，nb为本底计数率,ts为样品测量时间,tb为本底测量时间,ρs为样品计数率平均值,ρb为本底计数率平均值,ρn为净计数率的平均值。则：

Nn=Ns-Nb

(10)

(11)

(12)

Ns和Nb服从泊松分布,所以：

(13)

(14)

(15)

(16)

(17)

由上可知，如果(9)式满足，则样品具有放射性。我们可以得到：

(18)

移项，开方，整理，可得：

(19)

(20)

(20)式中LD为探测下限。当净计数率的平均值为LD时，犯第二类错误的概率值等于小概率β值(即标称β值)。

2 修正系数

为了确认公式(3)和公式(20)的准确性，我们计算了相应探测下限犯第二类错误的实际概率值。在没有近似地情况下，已经发生衰变的放射性原子核数服从二项分布。当净计数率的平均值等于探测器净计数率的探测下限时，净计数率的随机数低于判断阈的概率即为犯第二类错误的概率值，为方便起见，公式(20)和公式(3)分别用公式(21)和公式(22)表示：

(21)

(22)

公式(21)用到的分位数为kα(或kβ)，公式(22)用到分位数为k1-α(或k1-β)，由于国内、国外对分位数的定义不同，在给定α或β的情况下，实际上分位数kα(或kβ)与k1-α(或k1-β)是相等的。公式(21)和公式(22)对应的判断阈值分别是公式(23)和公式(24)：

(23)

(24)

衰变了的放射性原子核数的判断阈值LCN为：

(25)

式中，η为仪器的探测效率。

(26)

式中，λ为衰变常量,N0为初始时刻的放射性原子核的数目，t为衰变时间，A为t时刻的放射性活度。

(27)

我们已经明确当净计数率的平均值是净计数率的探测下限时，净计数率的随机数低于判断阈值的概率值是犯第二类错误概率值，即当净计数率的平均值是净计数率的探测下限时，在给定探测时间内衰变的放射性原子核数的随机数低于衰变了放射性原子核数形式的判断阈值的概率是犯第二类错误概率值，所以我们可以得到犯第二类错误的真实概率值βreal：

(28)

根据文献[8]可知：

p=1-e-λts

(29)

我们以正常的分位数1.645、1.96、2.33为例，排列组合有9种情况，如表1所示。

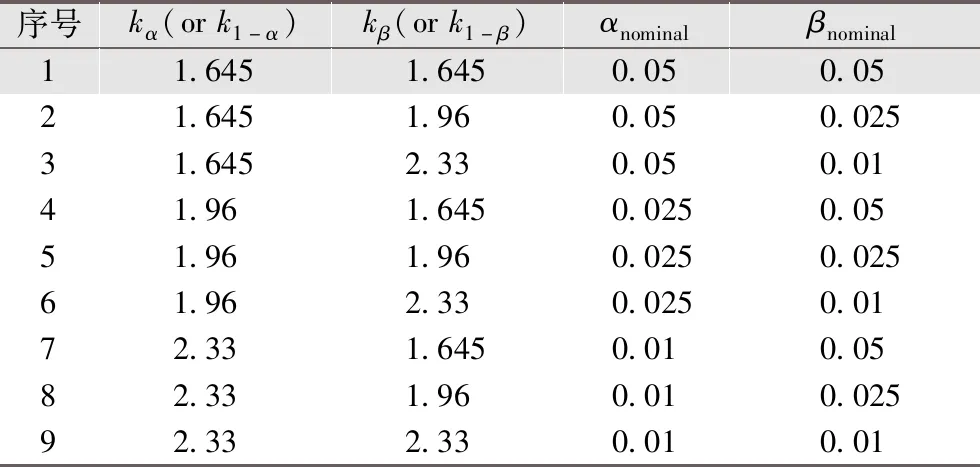
表1 分位数组合Tab.1 Quantile combination

以低本底α、β测量仪测量I-131为例，假设ts和tb满足(30)式，k可取1/60、1/50、1/40、1/30、1/20、1/10、1/5、1/2，1。以低本底α、β测量仪测量I-131为例，探测效率为60%(2π)，本底计数率从0.01到1 cps变化，步长0.01 cps。本底测量时间从10分钟到24小时变化，步长为1分钟。则

ts=k×tb

(30)

可以算出犯第二类错误实际概率值如表2所示。β1max是基于公式(21)算出的实际犯第二类错误的概率值的最大值。β2max是基于公式(22)算出的实际犯第二类错误的概率值的最大值，通过分析表2中的数据，可以发现实际犯第二类错误的最大概率值在大多数情况下比标称值0.05小1到2个数量级。在大部分实际探测需求中，我们并不需要这么低的误判概率，所以我们引入修正系数cor1和cor2对探测下限公式进行修正，使犯第二类错误的概率值趋近并略小于标称值，如(31)式和(32)式所示。

(31)

(32)

表2 实际犯第二类错误的概率值βrealTab.2 Actual probability value of making type II errors

1.961.6451/601/501/401/301/201/101/51/215.0×10-21.6×10-28.3×10-31.4×10-28.1×10-31.3×10-27.9×10-31.3×10-27.7×10-31.4×10-28.2×10-31.2×10-26.5×10-37.6×10-35.0×10-34.4×10-33.3×10-31.3×10-38.5×10-41.961.961/601/501/401/301/201/101/51/212.5×10-23.2×10-33.2×10-33.0×10-33.0×10-32.9×10-32.9×10-32.8×10-32.8×10-33.0×10-33.0×10-33.0×10-33.0×10-31.6×10-31.4×10-38.2×10-47.2×10-41.9×10-41.1×10-41.961.961/601/501/401/301/201/101/51/211.0×10-23.4×10-49.4×10-43.5×10-48.1×10-43.4×10-47.9×10-43.3×10-47.6×10-43.4×10-48.0×10-42.9×10-45.1×10-41.8×10-42.9×10-48.1×10-59.8×10-51.4×10-56.7×10-62.331.6451/601/501/401/301/201/101/51/215.0×10-21.5×10-24.3×10-31.4×10-24.2×10-31.4×10-24.2×10-31.4×10-24.3×10-31.5×10-24.1×10-31.2×10-24.4×10-38.4×10-33.6×10-33.9×10-32.7×10-32.2×10-31.4×10-32.331.961/601/501/401/301/201/101/51/212.5×10-23.2×10-31.5×10-33.2×10-31.4×10-33.1×10-31.4×10-33.0×10-31.5×10-33.20×10-31.4×10-32.7×10-31.4×10-31.8×10-31.0×10-37.3×10-45.5×10-43.4×10-41.9×10-42.332.331/601/501/401/301/201/101/51/211.0×10-23.8×10-43.8×10-43.7×10-43.7×10-43.6×10-43.6×10-43.5×10-43.9×10-43.8×10-43.3×10-43.3×10-43.1×10-42.2×10-42.0×10-47.5×10-56.9×10-52.7×10-51.4×10-5

通过计算，表3给出了kα=1.645，kβ=1.645时的修正系数cor1和cor2。

表3 修正系数Tab.3 Correction coefficient

如表3所示，引入的修正系数cor1和cor2小于等于0.78，即对探测下限的实际降低效果大于等于22%。以我们工作中常见的探测场景为例：

样本探测时间ts=24 h；本底探测时间tb=24 h；kα=kβ=1.645(标称值0.05)；ρb=2.0 cpm；nb=1.995 cpm；ns=2.169 cpm；nn=0.174 cpm。

通过公式(21)、(22)可计算得到优化前的探测下限LD1=0.177 cpm；LD2=0.178 cpm。而引入修正因子优化后的探测下限降低为LD1′=0.136 cpm；LD2′=0.137 cpm。显然净计数率nn=0.174 cpm小于优化前的探测下限LD1和LD2，此计数率会被作为无效计数率处理，视为仪器未检出放射性。但对应于优化后的探测下限公式，由于其大于优化后的探测下限，此计数率会作为有效计数率参与后续计算，视为仪器检出放射性。因此引入修正因子修正后，能够明显地降低探测下限，提高低本底α、β测量仪使用性能。

3 结论

本文从不等式角度推导了净计数率的探测下限，为验证公式的准确性，可以计算探测下限对应的实际犯第二类错误的概率值，大多数情况下，实际犯第二类错误的最大概率值比标称值小1到2个数量级，所以我们可以对探测下限进行修正，给出一个合适的修正系数，通过计算发现，当kα=1.645，kβ=1.645给出的修正系数可以使探测下限降低22%，而实际犯第二类错误的最大概率值趋近并略小于标称犯第二类错误概率值。