基于PSO-SVM模型的物流业景气指数组合预测研究

2021-01-28陈东清黄章树叶翀

北京邮电大学学报(社会科学版) 2020年6期

陈东清，黄章树，叶翀

(1.福州大学至诚学院，福建福州 350002;2.福州大学经济与管理学院，福建福州 350108)

我国经济处在由数量扩张向高质量提升的发展阶段，调整产业结构、助力经济发展成为各级政府、企业和公众的关注重点。而物流业景气指数是反映物流行业运行情况的优良指标，也是监测宏观经济发展状况的先导指标之一。科学预测物流业景气指数有助于提前预警物流业运行态势，同步甚至超前了解物流市场发展走向，为企业经营决策提供参考，为政府制定相关经济政策提供部分数据支持。因此，研究物流业景气指数预测方法及物流波动趋势显得尤为重要。

许多学者选择不同方法预测物流业景气指数。舒服华等[1]采用VAR模型对中国物流业景气指数进行预测，模型结果较为理想；孙颖[2]运用 ARMA模型预测我国物流业景气指数，从预测结果可以看出，当期物流业景气指数会受到前期指数的滞后影响；罗涛[3]选择VEC模型分析物流业景气指数与生产者价格指数的关系，从脉冲分析和方差分解发现，物流业景气指数的变动主要来源于自身变化的影响，因此预测该指数需要考虑自身的滞后影响。经典的经济预测方法还有回归分析及改进理论[4]、马尔科夫理论[5]、灰色预测模型[6]、系统动力学模型[7]、GARCH模型[8]、ARCH模型[9]、神经网络理论[10]、极限学习机理论[11]、语言策略方法[12]、非线性动态因子模型[13]等。

总体上看，物流业景气指数预测研究有所成就，但是还有不少需改进完善的空间：(1)物流业景气指数预测属于较复杂的建模问题，应优先考虑非线性建模技术，这就面临参数选择问题；现有一些研究通过凑试法选择参数，增加大量的建模工作量且存在一定的随意性，因此需要借助相关优化理论对参数进行智能选择；(2)当前关于物流业景气指数的单一预测方法或者组合预测方法，每个单一模型的训练集和测试集都是固定的，如果预测的步长太大，因建模信息远离预测点，则较难获得良好的测试(预测)精度。

鉴于此，本文采用粒子群算法(Particle Swarm Optimization, PSO)优化支持向量机(Support Vector Machine, SVM)参数，提出PSO-SVM模型的物流业景气指数组合预测方法，动态调整单一预测模型的训练集和测试集，构建多个单一PS0-SVM模型。每个模型外推预测两期，相邻两个单一模型平均值作为模型测试(预测)值，以福建省数据为样本进行实证研究，验证模型的有效性。

一、预测模型的选择

(一)v-SVM回归方法

标准支持向量回归机考虑了线性和非线性情况。对于非线性情况，通过非线性函数的变换，把样本数据映射到高维空间，根据核展开定理求解问题时，无需知道非线性映射的显性表达式，从而简化模型计算，避免了所谓的“维数灾难”问题。标准支持向量机模型可以通过调整ε值控制回归的精度，但是由于ε值没有明确的含义，导致模型估计时难以确定ε值。因此，有的学者对此问题进行研究改进：Scholkopf等[14]提出v-SVM，采用参数v代替ε，在一定程度上方便了支持向量回归机参数调整[14]，拓展支持向量回归机的应用。关于v-SVM模型的参数v，邓乃扬等[15]证明了参数v的取值范围以及含义，具体如下。

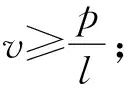
由以上结论可得，v-SVM模型参数v的取值范围为[0,1]，并且可以通过选择v值控制错误样本点，或者支持向量的个数，因此v有比较明确的含义。这对参数的选择有重要意义，意味着v-SVM相对于标准支持向量回归机有一定的优越性。

支持向量机是基于有限样本发展的机器学习理论，综合考虑了建模的复杂程度以及学习能力，具有较强的泛化能力[16]，对于有限样本的预测问题具有很强的优势。中国物流与采购联合会和中国物流信息中心于2013年3月联合发布了中国物流业景气指数[17]，是一个较新的宏观统计指数，数据量有限；另一方面，物流业景气指数受到的影响因素较多，并且存在非线性影响关系。v-SVM模型良好解决了有限样本、非线性的问题[18]，且v参数含义明确，方便模型参数调整。因此，本文选择v-SVM回归方法作为物流业景气指数预测的基础模型。

(二)粒子群优化算法

粒子群算法是由Kennedy和Eberhart等学者受鸟群觅食行为启发提出的优化理论，是一种效率比较高的优化技术。假设在D维搜索空间中，某个微粒群有m个微粒组成，在搜索空间内的粒子i在t时刻的状态信息如下[19]

(1)

(2)

(3)

(4)

(5)

式(5)是最原始的粒子群算法，c1、c2为学习因子或者加速系数，取值通常为c1=c2=2；r1、r2取值为均匀分布在[0，1]范围内变化的随机数。

为了提高原始粒子群算法的收敛速度以及取得更好的解，Shi等[20]提出了带有惯性权重的PSO模型。对于上述的速度公式改进如下

(6)

式(6)中，称w为惯性权值，w的大小衡量该粒子对当前速度的继承量，使PSO算法具有强局部搜索能力。线性递减公式如下

(7)

Shi等[20]建议w的范围从0.9线性递减到0.4。因此，式(7)中wstrat取值为0.9，wend取值为0.4；tmax为最大的迭代次数，tnow为当前的迭代次数。

(三)基于粒子群优化的支持向量机回归模型构建思路

在支持向量机回归模型中，惩罚系数以及核函数参数是影响模型精度的主要参数；如果采用凑试法或者网格搜索法，参数寻优效率较低。本文采用带有惯性权重的粒子群优化算法，以交叉验证意义下模型的均方根误差最小作为函数优化目标，寻找满意的惩罚系数以及核函数参数；并对模型进行训练和测试，以期得到满意的模型结果。如果模型结果较差，则需要重新考虑被预测变量的影响因素，重新建模，直至得到满意的模型结果。

二、基于PSO-SVM的物流业景气指数组合预测模型构建

根据时间序列分析理论，本期物流业景气指数受到前几期指数的影响，可利用前几期物流业景气指数构建模型预测本期物流业景气指数；为了提高预测精度，同时考虑春节因素以及疫情因素对物流业景气指数的影响。借鉴组合预测的思想，构建PSO-SVM组合预测模型，主要思路是：首先，从时间序列分析视角确定物流业景气指数的主要影响因素，采集研究数据集；其次，将总数据集划分为训练集和测试集，构建PSO-SVM预测模型，并用粒子群算法对参数进行寻优，构建预测精度较高的单一预测模型；再次，动态调整训练集和测试集，重新构建多个单一预测模型，每个模型进行两步预测，以单一模型拟合值的平均值作为总体建模样本的拟合值，以临近两个模型预测结果的平均值作为测试值；最后，检验模型的精度，如果模型精度满意，则可用于预测未来物流业景气指数，否则分析研究问题，重新构建模型。模型构建流程如图1所示。

物流业景气指数为

y(t),(t=1,2,…,m)

(8)

设物流业景气指数的n个主要影响变量为

Xi(t)={x1(t),x2(t),…,xn(t)}

(9)

其中，xi(t)代表第i个影响因子(影响因子可包含滞后的影响因素)，t代表序列的编号，如x1(1)的含义为第一个影响因子第1序列的值。

1.划分数据集

将所要研究的数据集根据特定的规则划分为测试集和训练集，并构造外推预测需要的预测集。本文将整理好的研究数据集称为总数据集，包含训练集、测试集、预测集三部分，分别记为S、T、P。其中，训练集S为总数据集的前p个样本数据，测试集T为总数据集的第p+1个样本数据起到第m个结束为止，测试集T的数据样本个数为k(k=m-p)，预测集P只含有影响因子，用于对未来物流业景气指数的预测。需要说明的是，训练集和测试集的样本个数是相对于整个总体模型而言，确定了用于测试的数据集样本个数，则训练集的样本个数也随之确定。

2.构建第一个预测模型(记为Model-1)

在模型Model-1中，训练集S为总数据集的前p个样本数据，测试集T为总数据集第p+1个到第m个样本。对于Model-1预测模型，训练集和测试集的划分如表1所示。

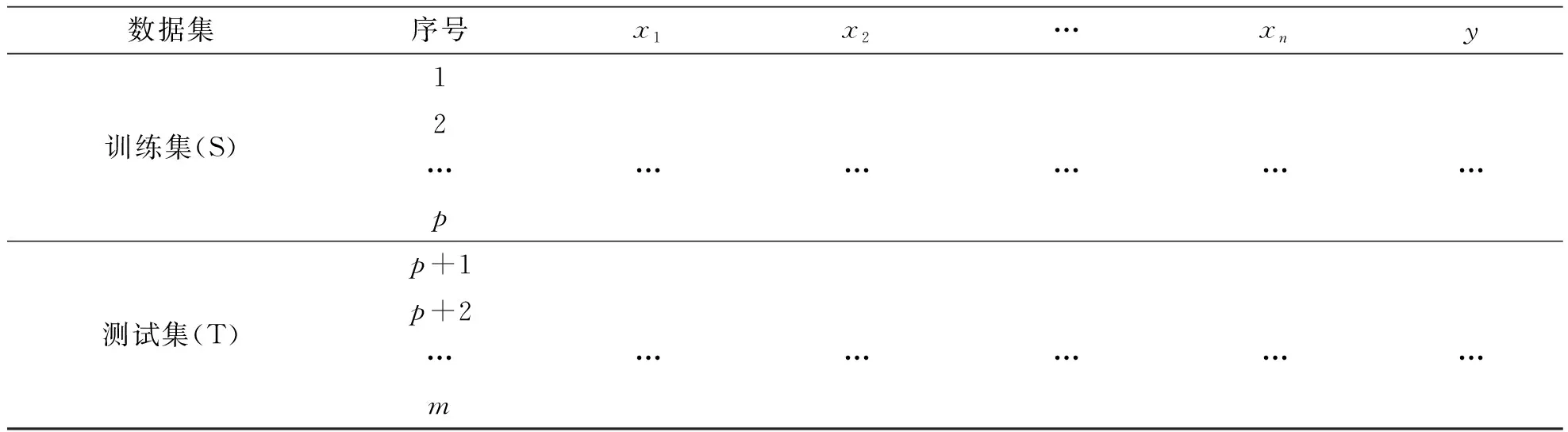
表1 Model-1训练集和测试集的划分

3.计算单一模型结果

4.重新划分单一PSO-SVM的训练集和测试集

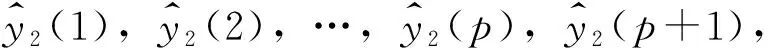
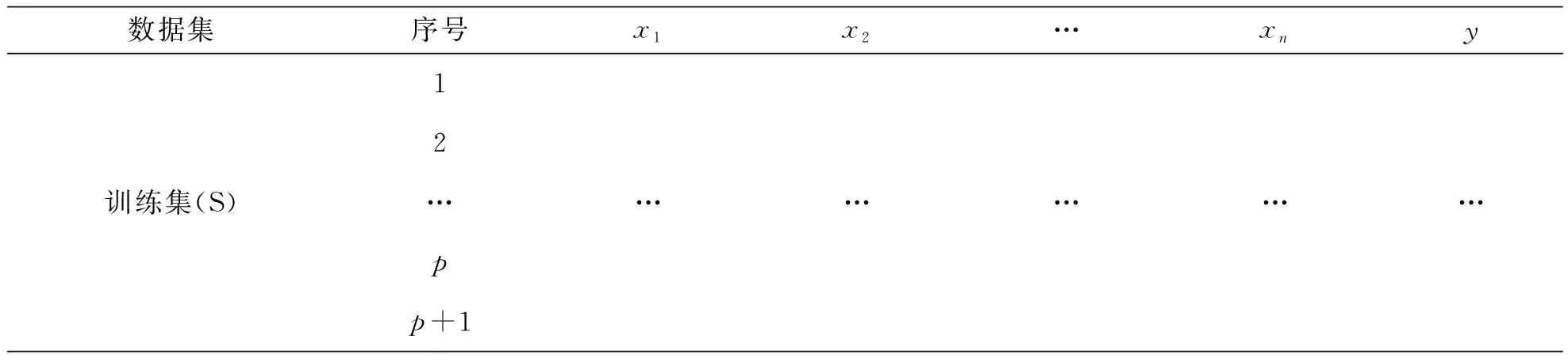
表2 Model-2训练集和测试集的划分

续表

5.重复步骤

重复第三、第四步骤，直到把前m-1个数据集都作为训练集，第m个数据作为测试集结束，此时一共构建了k(k=m-p)个预测模型，并进行了两步预测(最后一个模型只需进行一步预测)，具体如表3所示。

6.计算总数据集的拟合值和测试值

利用上述所构建的模型Model-1，Model-2，…，Model-(m-p)计算得到各个模型的拟合值，对模型拟合值求平均值作为总体样本的拟合值。整理每个单一模型的两步预测，结果如表3所示。整体样本的第一个测试值为 MODEL-1进行一步预测得到的预测值，从第二个测试值起，其测试值为前一模型进行二步预测的预测值和当前模型进行一步预测的预测值的平均数，具体计算方法见表4。

7.检验模型精度

采用均方根相对误差评价模型的总体建模精度，如果模型精度较高，则可用于未来物流业景气指数的预测；如果模型精度不理想，则重新寻找影响因素，再次构建模型，直到获得满意的模型效果。

8.模型应用

将构建的模型应用于未来物流业景气指数预测，预测值仍然采用测试阶段测试值的计算方法。

三、福建省物流业景气指数实证预测

(一)数据来源

福建省物流业景气指数由福建省工业和信息化厅与福建省物流协会联合发布，从2014年4月起每月在福建省经济信息中心网站公开发布，数据权威性高。本文所采用的样本区间为2014年4月至2020年7月的月度数据，如表5所示。

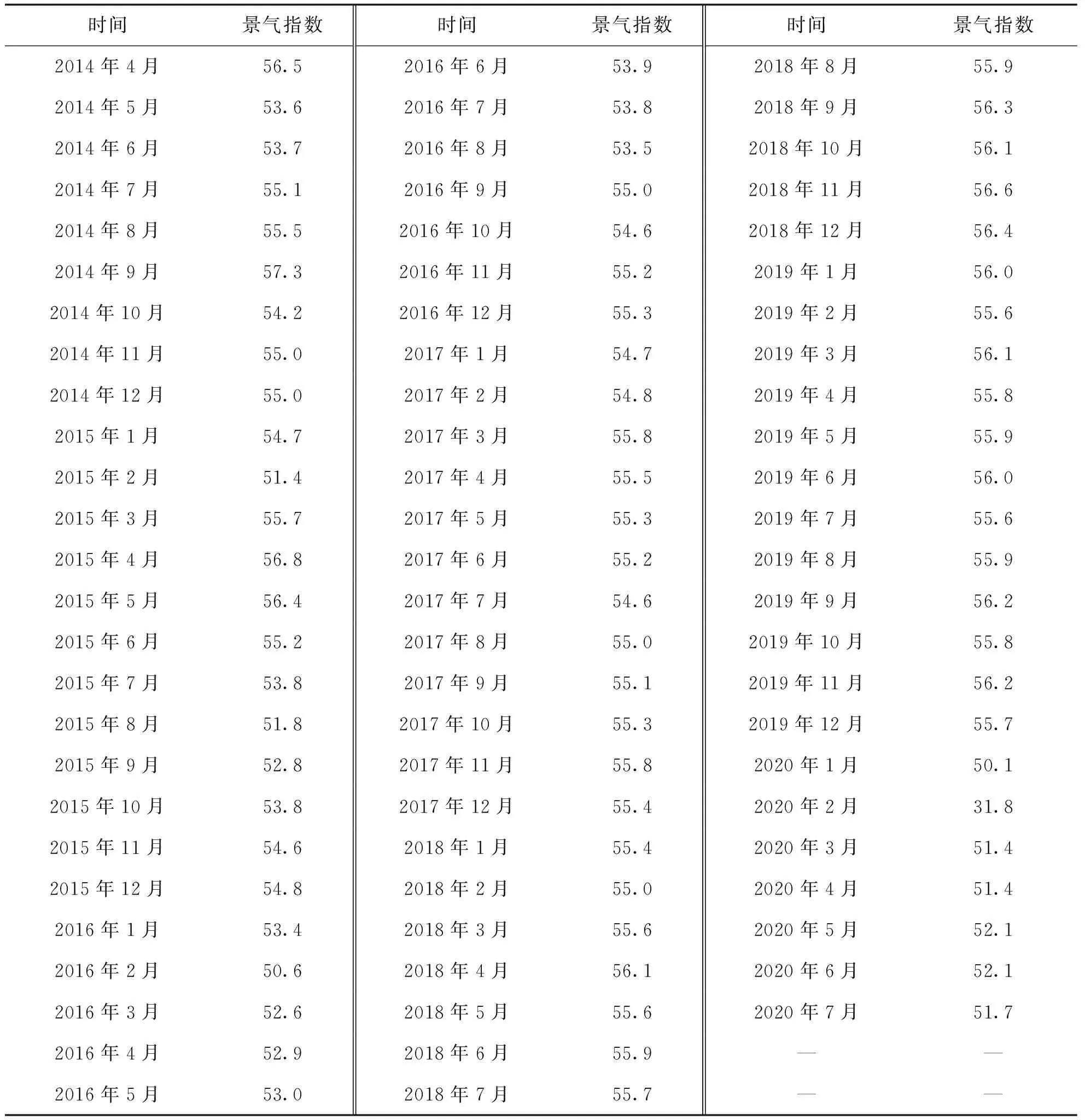
表5 2014年4月—2020年7月福建省物流业景气指数

考虑到春节因素对物流业发展的影响，引入虚拟变量，如果该月份含有春节假期则虚拟变量取值为0，否则取值为1。2020年，新冠肺炎疫情对我国经济产生了影响，也对物流业发展产生冲击，因此本文引入新冠肺炎疫情对物流业发展的影响变量，该变量值越大，代表疫情对物流业景气指数的负向影响作用越大。2019年(含)之前的月份，变量的取值为0，2020年1月至2020年10月的影响变量取值如表6所示，影响程度取值说明如下。

面对突发疫情，2020年1月24日，福建省启动重大突发公共卫生事件一级响应，1月份物流业发展不确定性增强，同时考虑春节因素的共同交叉影响，故影响变量取值为4；自2020年2月26日起，福建省根据地区风险差异，调整新冠肺炎疫情防控等级为省级二级响应或者三级响应，2月份一级响应的天数多，故2月份的影响变量取值为4；自2020年3月19日起，福建省新冠肺炎疫情防控应急响应等级统一调整为省级三级响应，3月份福建省防控措施仍较为严格，故3月份的影响变量取值为3；2020年4月份，福建省新冠肺炎疫情防控应急响应等级均为三级，故4月份的影响等级取值为2；从2020年5月(含)起，物流经济活动逐渐恢复，但仍受到疫情影响，并且预计未来几个月疫情相对稳定，故2020年5-10月的影响变量取值为1。

表6 新冠肺炎疫情对物流业的影响程度取值

(二)数据预处理及参数设置

本文采用常用的三倍标准差(3σ)原则[21]识别异常值。2014年4月至2020年7月，物流业景气指数均值正负3倍标准差的区间为[45.224 9, 63.617 2]，故偏离此区间的值判定为异常值。受到新冠肺炎疫情的影响，福建省2020年2月份物流业景气指数为31.8，偏离区间范围，属于异常值，其余数据均落在上述区间范围。为了消除异常值对模型精度的影响，2020年2月物流业景气指数由2020年1月份和3月份的平均值处理得到，为50.75，后续的模型运算均按此数值进行。

为消除建模数据的量纲差异，采用以下公式对数据进行标准化处理，经过处理后数据规范化到[1,2]之间，可得

(10)

式(10)中，xmin为变量x的最小值，xmax为变量x的最大值。

本文对数据集进行随机划分，选择5个样本作为测试数据，并确保测试样本中有且仅有1个样本是受疫情影响的样本数据(即2020年1-7月的样本数据)，其余样本作为建模数据。设置粒子群优化算法的最大迭代次数为200，种群数量为20，采用4折交叉验证，其他参数的初始值采用本文介绍的粒子群方法推荐的初始值。支持向量回归机的惩罚系数C综合权衡模型拟合能力和泛化能力，C值越大则模型结构风险越大，经验风险越小，容易出现过拟合现象；C值越小，则模型结构风险越小，经验风险越大，容易出现欠拟合现象。兼顾模型优化时间和预测精度，支持向量回归机惩罚系数C的区间设置为[0.1,100]，v参数的区间设置为[0.4,0.8]。

核函数是影响支持向量机性能的关键因素，可划分为全局核函数和局部核函数两大类型。全局核函数的泛化能力具有优势，但学习能力较弱，如线性核函数、多项式核函数、Sigmoid核函数；局部核函数影响相距较近数据点[22]，学习能力强，但泛化能力较弱，如RBF径向基核函数。本文构建的单一PS0-SVM只进行两步预测，预测步长较短，因此优先选择RBF径向基核函数，设定RBF核函数参数σ的区间设置为[0.01,100]；另一方面从实证分析结果发现，采用RBF核函数构建的支持向量机模型建模阶段及测试阶段的精度均较高，说明选择RBF径向基核函数作为所构建模型的核函数可行。

(三)滞后阶数的选择

滞后阶数的选择会很大程度影响预测模型的精度，如果选择太短可能会导致精度较低，反之会增加模型运算的复杂程度。当期物流业发展态势容易受到前期发展状态的滞后影响，且当期的物流业运行状态对未来物流业走势的影响程度呈现衰减趋势，故本文设定最大滞后影响期数为4。

借助Matlab 7.9.0工具编程实现所构建PSO-SVM组合预测模型的计算，模型参数按照上一步介绍参数设置，采用粒子群算法以交叉验证意义下模型的均方根误差最小作为函数优化目标。图2显示滞后阶数为1时，第5个单一预测模型参数的寻优过程。可以直观看出，随着迭代次数的增加，最佳适应度曲线趋于稳定；平均适应度曲线波动小，模型性能趋于稳定；最终探索得到模型最佳惩罚系数C为0.7181，RBF核函数参数σ为19.587 2。限于篇幅原因，其他不同滞后阶数模型的参数寻优过程不再赘述。

整理得到不同滞后阶数对应模型的拟合误差和测试误差，如表7所示。建模阶段模型的均方根相对误差从小到大排序对应的滞后阶数为1，2，3，4阶，测试阶段模型的均方根相对误差从小到大排序对应的滞后阶数为1，4，2，3阶。综合四个模型结果，滞后阶数为1模型的拟合误差和测试误差均最小，并且测试误差明显优于其他3个模型，说明该模型的泛化能力明显较强，因此模型的滞后阶数选择为1。

表7 不同滞后阶数预测模型结果分析

(四)模型结果分析及应用

图3是模型的拟合以及测试结果，○标记的为原始值，*标记的为建模阶段的拟合值，+标记的为测试阶段的测试值，图4为每个样本的拟合值及测试值的相对误差图。可直观看出，大部分样本的拟合相对误差保持在3%以内(两条直线代表相对误差为-3%和3%)，建模阶段的均方根相对误差为1.26%，说明该模型能够较好拟合原始数据。但有两个月份的拟合误差偏大：2014年5月的拟合相对误差为-4.47%，该月份受到五一劳动节和端午节两个法定节假日影响，物流活动活跃度下降，导致实际值比拟合值小且偏离较多；2015年8月的拟合相对误差为-4.34%，该月份福建省受高温、台风多雨天气影响，物流业景气度回落，导致实际值比拟合值小且偏离较多。

为了进一步验证模型的效果，对模型进行测试，测试结果如表8所示。模型测试值最大相对误差在1%左右，测试阶段的均方根相对误差为0.82%，说明模型测试效果良好。

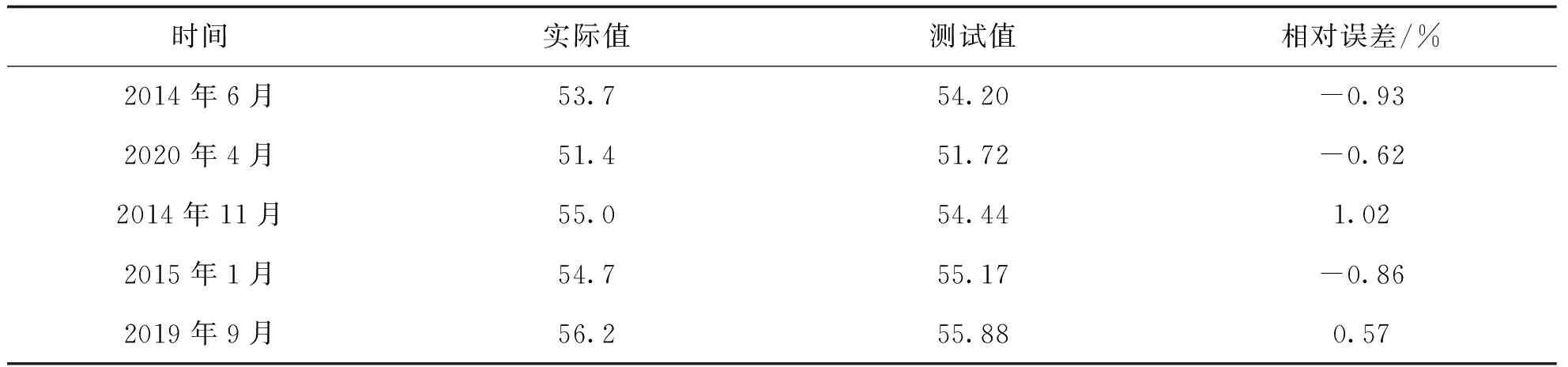
表8 模型测试结果

为了检验模型的通用性，将本文提出的PSO-SVM物流业景气指数组合预测模型应用到浙江省物流业景气指数预测。从公开数据发现，浙江省2014—2015年物流业景气指数采用季度数据的方式公布。2016年1月起采用月度数据方式公布，为保持建模数据的一致性，选择浙江省2016年1月至2020年7月的物流业景气指数数据验证模型，数据预处理方式及初始参数设置均按照上述过程进行。整理得到不同滞后阶数，浙江省物流业景气指数预测模型的精度如表9所示。从表中可看出，滞后阶数为4所对应的预测模型拟合误差和测试误差均最小，并且均方根相对误差都小于3%，模型总体精度满意，可用该模型预测浙江省物流业景气指数，说明本文构建的PSO-SVM物流业景气指数组合预测模型具有较好通用性。