基于LQR的飞机纵向控制律设计
2021-01-28牛文韬黄清顺
牛文韬,高 永,黄清顺
(海军航空大学,山东烟台264000)
飞机控制系统设计主要包括2 种方法:经典控制理论方法和现代控制理论方法。其中,经典控制理论研究方法以频域法和根轨迹法为代表,本质上是借助于大量直观经验,按照闭环回路控制原理,依次选择控制系统的结构参数;同时,对于飞机的非线性和参数变化问题,采用线性化处理和调参处理等方法加以解决;最后,通过不断地仿真和模拟试验优化,得到一个良好的控制系统。但是,对于具有更多回路或者多输入、多输出的飞行控制系统以及现代战斗机的高度非线性等问题,经典控制理论已不能满足实际需求。而现代控制理论可以得到系统的状态变量模型,相比传递函数模型,它包含了更多的系统信息。因此,可以得到更为优异的控制性能;同时,该模型可以使多个控制回路同时闭合,并自动地协调各回路性能,在飞行控制系统的设计中占据越来越重要的地位[1-2]。
20世纪50年代以来,以线性二次型调节器为核心的最优控制设计方法,已经成为一种应用较广、较成熟的飞行控制系统设计方法。20世纪70年代,美国成功运用显模型跟踪最优二次型法设计了F-8C 主动控制验证机的控制律;80 年代,美国设计了隐模型跟踪最优二次型与经典法相结合的控制律,并应用于X-29上;X-31飞机的大迎角机动控制律也采用了最优二次型法。这种方法的控制对象是线性系统的状态空间函数,并以状态和控制输入的二次型函数为优化目标,目的是设计合适的状态反馈增益矩阵K ,使目标函数取得最小值。K 值由加权阵Q 和R 决定,所以Q和R 的选择是求解问题的关键。
利用LQR 理论设计的控制律是反馈状态变量的线性函数,可以实现闭环最优控制。由于方法简单且便于实现,还可以利用Matlab 等软件进行仿真计算,在工程实践中已得到大量运用[3-7]。应用最优二次型法设计控制律,一般按照如下的程序进行:
1)简化非线性系统模型,设计飞机响应的开环构型;
2)根据简化模型设计控制律;
3)加入被忽略的高频动态环节和非线性特性等,修正系统特性;
4)对设计的飞行控制系统进行飞行品质的仿真实验,进一步完善系统。
本文以某型固定翼飞机的纵向小扰动模型为基础,以C*响应准则为目标,利用显模型跟踪最优二次型法对飞机的纵向控制律进行设计,并进行了仿真验证。在此基础上,利用低阶等效系统方法对飞行品质进行了评价。
1 飞机纵向动力学模型建立
为得到飞机的操纵性及动态响应,须建立飞机飞行动力学模型,并进行小扰动线性化处理,得到机体坐标系下的纵向小扰动运动方程如下[8]:

飞机纵向运动包含长周期和短周期2个模态。其中,短周期模态速度的变化可以忽略,主要体现在迎角和俯仰角速度的快速变化,短时间对飞行员的操纵提出了很高的要求;而长周期模态变化周期长,飞行员常在无意识情况下就修正了飞机姿态,所以本文只考虑飞机的短周期模态。
假设在纵向的操纵运动中,油门杆的位置δp和飞机飞行高度H 始终保持不变,得到飞机的短周期方程为:

本文所设计的控制律为实现常规飞机响应,选用过载和俯仰角速率的组合反馈。法向过载与迎角的关系为:


由实际的飞行经验可知:飞机在低速飞行过程中,法向过载的变化可忽略,飞行员更多地感受到俯仰角运动的变化,并通过俯仰角速率响应来操控飞机;当飞机高速飞行时,法向过载的变化过大,飞行员通过过载响应操控飞机。由此提出2种状态的混合响应来进行飞行品质的评价,即C*响应[9],定义为:

式(5)中:vco为交叉速度,此时飞行员对二者的感觉相同,其值一般为120~132 m/s。飞行员不在飞机质心,因而要考虑角加速度形成的过载,故:

式(6)中:l 即为飞行员到质心的距离。
由此可得到C*的状态空间表达式:

对式(4)、(7)进行拉普拉斯变换,并假定初始条件为0,则有:
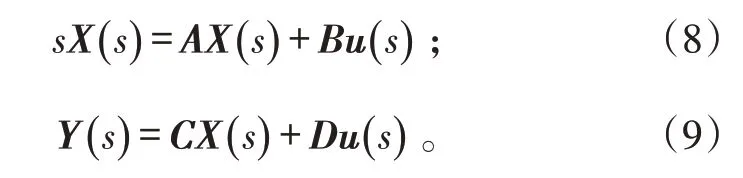
可得C*传递函数:
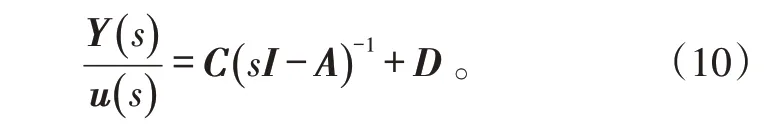
图1为C*开环响应结构。

图1 C*开环响应结构Fig.1 Structure of open-loop response of C*
依据图1可得,C*对操纵杆的传递函数为:

当输入为1 g 时,C*的开环阶跃响应如图2所示。
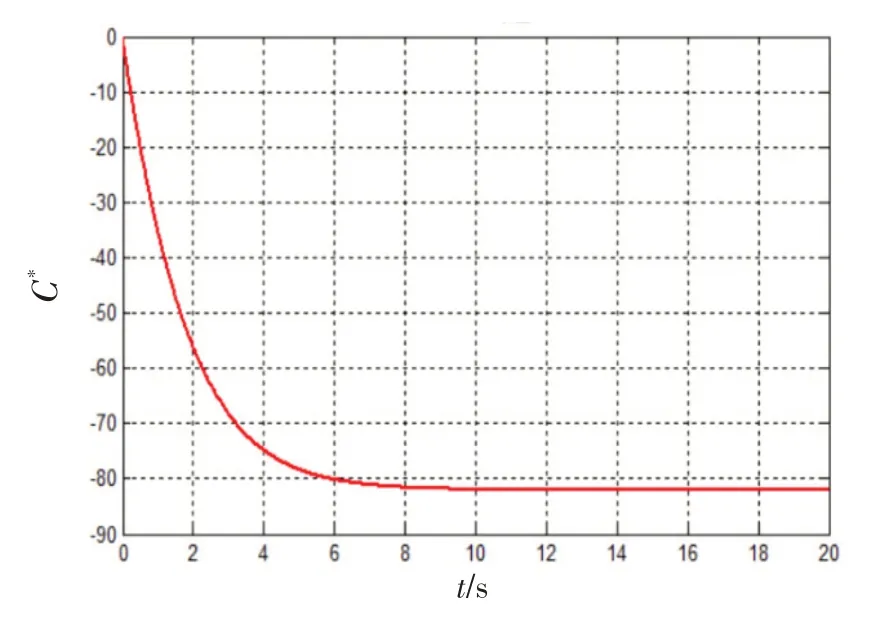
图2 C*开环阶跃响应Fig.2 Open-loop step response of C*
图3为杆力输入为1 g 时,C*响应准则。
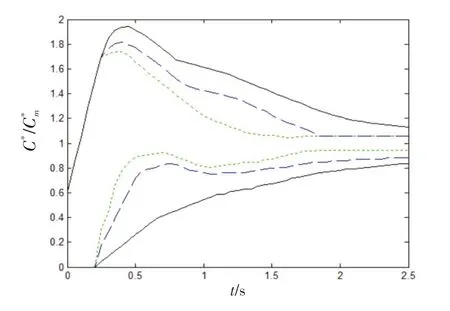
图3 C*响应准则Fig.3 Response criterion of C*
根据图3 所示的响应准则,对图2 的C*响应进行评价,结果如图4所示。
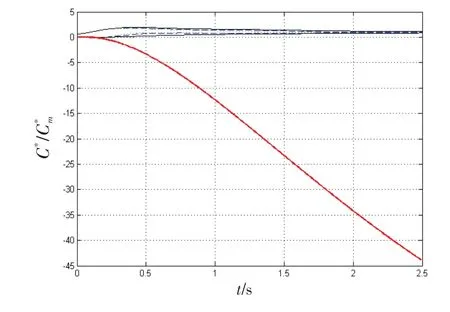
图4 开环C*响应评价Fig.4 Evaluation of open-loop C*response
由图4可知,飞机的开环C*响应不在理想C*值的包线范围内,飞行品质不符合要求,下面对飞机进行闭环控制律设计,以改善飞机的飞行品质。
2 LQR最优控制器理论
最优二次型设计包括输出反馈的最优二次型、显模型跟踪最优二次型和隐模型跟踪最优二次型等。本文采用显模型跟踪最优二次型法对飞机的纵向控制律进行设计。模型跟踪最优控制是指对被控对象,选择合适的控制作用,使闭环系统的输出能够跟踪给定的理想模型,同时使代价函数最小,数学模型如下[10-12]:
设系统的状态方程为:

响应向量方程为:
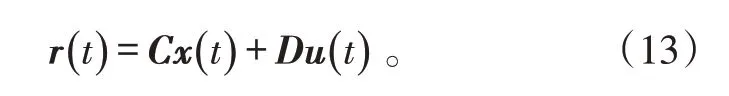
式(12)、(13)中:x ∈ℝn为状态向量;u ∈ℝm为输入向量;η ∈ℝq为随机白噪声过程向量;r ∈ℝR为输出向量;A、B、C、D 为系统矩阵;F 为随机扰动矩阵。
最优二次型指标函数为:

式(14)中:Q1=CTQC ;Q2=CTQD ;Q3=DTQD ,且加权阵Q 为正定或半正定矩阵。
最优控制可表述为,选取

使得最优二次型指标函数J 最小。其中最优控制增益K :

式(16)中,P 为下述代数黎卡堤方程的解:

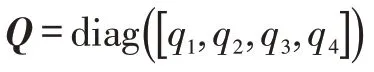
3 控制律设计
在控制律设计过程中,考虑了飞机高频环节对响应的影响,包括舵回路的高频动态特性和舵偏角限制的非线性特性,角速率陀螺、杆力传感器自身的动态特性,在系统特定位置的结构陷波器动态特性。此外,数字式电传操作系统的延时特性也应该考虑[13-15]。
设计飞机的纵向控制结构如图5所示。为实现C*响应的显模型跟踪,按飞行品质要求,设计了理想C*响应模型。通常C*响应模型可由一个2阶环节表示:
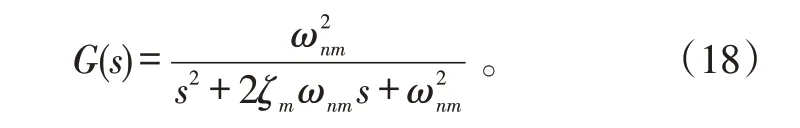
本文取ωnm=7.9 rad/s,ζm=0.9。其值满足MILF-8785C的一级飞行品质要求。

图5 飞机闭环控制Fig.5 Closed-loop control of aircraft

最优控制律采用全状态反馈,含8 个状态,从图5可以得到系统的各个状态变量之间的关系:
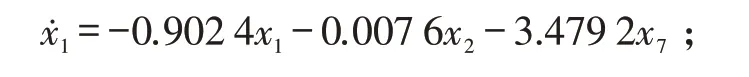

把上述各变量代入系统的状态方程,可得:
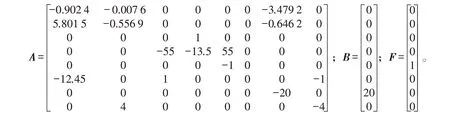
系统响应分别取C*响应与理想模型的跟踪误差、误差积分、升降舵面偏转及控制输入4个变量:
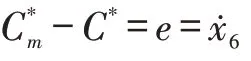
r2误差积分:x6;
r3舵面偏转:x7;
r4控制作用:u(t)。
由式(12)可得:

加权阵Q 的选择并没有规律可以遵循,而且不唯一,由于Q 矩阵对飞行品质的影响目前仍不明确,故通常的做法仍是不断地对矩阵中的元素进行分析、试凑来确定。一般取Q 矩阵为对角阵,某个元素增大即增大对该响应分量的加权。在经过仿真计算得出反馈增益K 后,还要进行飞行品质的评价,以确定所选Q 阵是否满足要求[16-19]。此处选取:


给系统施加阶跃激励,利用Simulink 进行最优控制仿真的仿真框图如图6所示。

图6 仿真框图Fig.6 Diagram of simulation
并根据图3对C*响应的飞行品质进行评价,仿真和评价结果如图7所示:
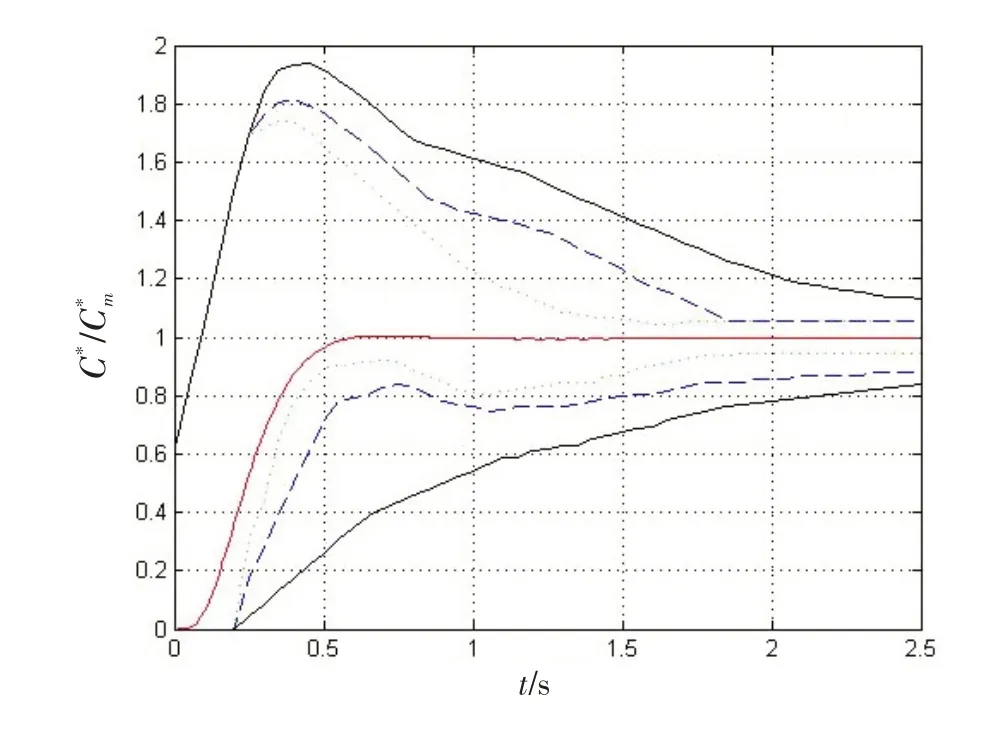
图7 闭环C*响应评价Fig.7 Evaluation of closed-loop C* response
同时选取系统8 个状态量中的4 个状态量,仿真结果如图8~11所示。
由图8~11 可知:实际C*响应与理想C*响应基本重合,C*误差最大值为0.08,并且在3 s 左右达到稳定。最大舵偏角为0.01 rad 左右,远小于非线性限制,符合最优控制律的设计要求。
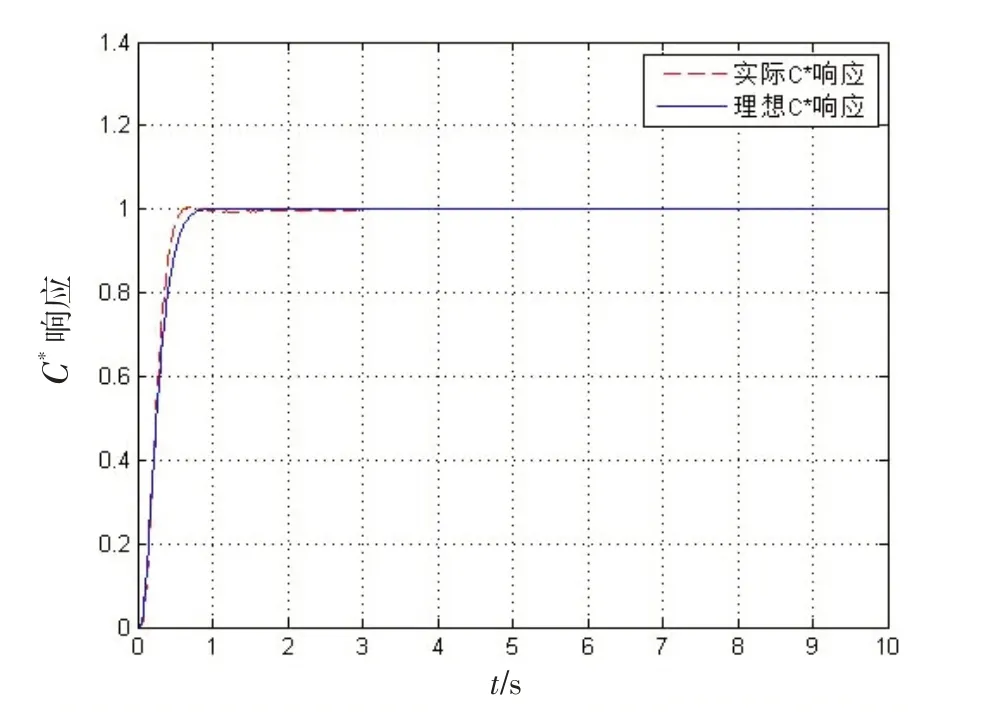
图8 实际C*与理想C*响应Fig.8 Actual C* response and ideal C*response
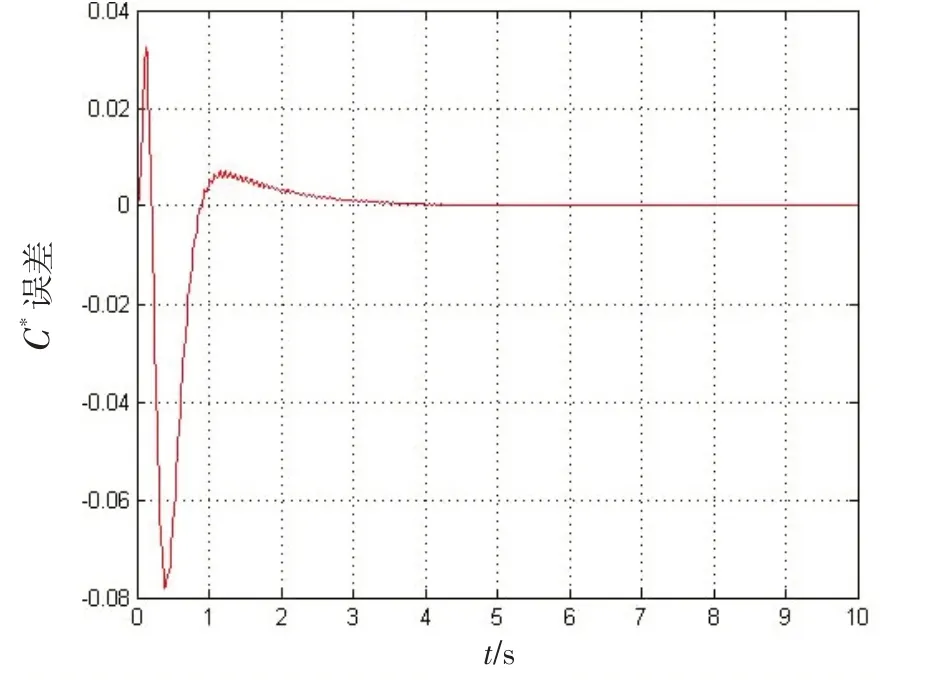
图9 C*误差响应Fig.9 C* error response

图10 俯仰角速度响应 Fig.10 Pitch rate response
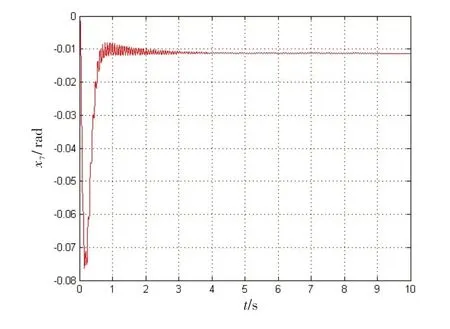
图11 升降舵偏角Fig.11 Elevator deflection angle
4 飞行品质验证
在C*响应评价的基础上,进一步对飞机的飞行品质进行验证。针对第3节加入高频环节的飞机控制系统,本节利用低阶等效系统方法对飞机的飞行品质进行评价。高阶飞机的低阶等效系统是指2个系统在相同的初始条件和外界输入下,在一定时域或频域内,二者的输出差值在给定的指标函数下最小。该等效系统可用频域或时域拟合的方法求得,具体的频域等效原理如式(20)所示:
寻求GLOES( )jω 中的参数,使下述指标函数最小:
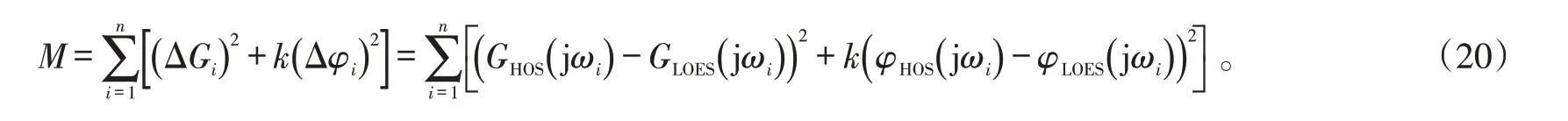
本文对法向过载和俯仰角速率进行双拟配。为得到飞机的频率响应,在式(20)的基础上,给出飞机俯仰轴上的法向过载与俯仰角速率的等效传递函数:

式(21)、(22)中:Fe为杆力输入;kq、knz为增益,τq、τn分别为q、nz的等效延迟时间;Tq为时间常数。
根据式(20)~(22)即可求得低阶等效系统中的各参数。具体的拟配条件为:
拟配时飞机的飞行状态为:高度5 km ,速度1.0 Ma;
飞机的飞行阶段则选取:C 阶段,即场域飞行阶段;
拟配结果见表1所示。

表1 等效拟配结果Tab.1 Equivalent fitting result
根据GJB 185-86有人驾驶飞机飞行品质要求,给出了短周期运动的阻尼系数等级评判标准和巡航阶段CAP标准,见表2以及图12。由表2可知,该飞机短周期运动的阻尼系数基本达到一级飞行品质的要求;同时对于俯仰角速度和过载的等效延迟时间也基本满足一级飞行品质要求。由图12 巡航阶段CAP 标准[20]可知,该飞机在巡航阶段的操纵期望参数满足一级飞行品质要求,即能够顺利地完成各项任务。

表2 短周期阻尼系数等级标准Tab.2 Short period damping coefficient grade standard

图12 CAP评价准则Fig.12 Evaluation criteria of CAP
5 结论
针对飞机的纵向短周期响应不满足飞行品质要求的问题,利用最优二次型法设计飞机的控制律,对飞机的纵向响应进行反馈调节,设计了飞机的闭环控制响应仿真模型。仿真结果表明:所设计的控制律能够有效改善飞机的飞行品质,且结构简单,具有良好的适用性。由于飞机控制系统是一个高阶增稳系统,所以,利用低阶等效系统法对该系统进行拟配,拟配结果表明:飞机的阻尼比、操纵期望参数能达到一级品质要求,即能够顺利地完成各项任务。
