RV 减速器摆线轮齿廓曲线的曲率影响因素研究

张跃明，王 巍，纪姝婷

（北京工业大学机械工程与应用电子技术学院，北京 100124）

1 引言

RV 减速器（Rotary Vector Reducer）是工业机器人的核心部件，而摆线轮是RV 减速器的关键零部件[1-2]。摆线针轮传动是一种新型传动，关系这种传动效率很重要的参数就是摆线轮齿廓曲线的曲率，对摆线轮齿形的设计至关重要。当前国内技术对摆线轮的设计方面还处于不完善状态[3-4]。摆线针轮行星传动也遵循齿轮传动的一般规律，在齿廓曲线拐点处传动性能较好，传动效率较高，曲率的变化情况直接影响齿轮传动的好坏[5]。对齿面磨损与润滑、计算轮齿的接触疲劳强度、接触区域的变形以及齿廓修形都有直接的影响[6]。目前，啮合线、重合度、传动误差在摆线针轮传动中都有学者研究[7-8]，还有一部分学者研究了渐开线齿轮的曲率变化情况[9-10]，文献[11]研究正交面齿轮传动中齿面曲率，推导了面齿轮传动的齿面主曲率和主方向；文献[12]研究了外压椭圆封头当量曲率半径，分析了当量半径的取值方法；文献[13]用包络法讨论了诱导法曲率，先讨论了相对法曲率和相对主曲率，最后讨论了诱导法曲率和综合曲率。虽然很多学者都对曲率进行了研究，但是对摆线轮齿廓曲线的曲率研究却很少，其中各参数的变化对摆线轮齿廓曲率的改变在国内参考文献中尚是一片空白。因此，有必要分析和探讨各参数对摆线轮齿廓曲线的曲率变化的影响，这对摆线轮齿廓修形、摆线针轮传动装置的设计和研发具有重要的指导意义。

针对摆线针轮行星传动机构的啮合特性，推导了摆线轮齿廓曲线的曲率和拐点解析式，详细分析了几何参数对拐点位置的影响规律，计算出在一个摆线轮齿廓凹凸区间上曲率最大值和最小值，并且深入研究了几何参数对曲率变化快慢的一般规律。

2 摆线轮齿廓

2.1 摆线轮齿廓方程

为摆线针轮行星齿轮传动机构，该机构主要由摆线轮、针齿壳和机架三部分组成，如图1 所示。根据摆线轮与针轮的相对运动关系，摆线轮既有绕针齿分布圆的中心公转，也有绕自身几何中心的自转，因此可以建立坐标系，如图2 所示。让坐标系XcOcYc与摆线轮固定，让坐标系XpOpYp与针齿壳固定在一起。研究的是针对针齿壳固定，所以固定坐标系X0O0Y0与针齿壳坐标系XpOpYp重合。在初始位置时，Xc轴与X0轴重合，Yc轴与Yp轴是平行的。由齿轮啮合原理可以知道，摆线轮与针轮之间的啮合传动，相当于摆线轮的节圆和针齿轮的节圆做内切的纯滚动。点P 为节点，如图是两圆初始啮合位置，初始啮合节点为P0，摆线轮的节圆圆心Oc绕针齿轮节圆圆心Op转过角度为θp，则小圆滚过的角度为θc，则可以得到动轴与定轴之间的夹角：Δθ=θc-θp。

图1 摆线轮齿廓曲线的形成Fig.1 The Formation of Cycloidal Profile Curve

在两圆转动过程中，针齿中心A 在动坐标系XcOcYc上形成的是短幅外摆线，实际摆线轮齿廓是短幅外摆线的内侧等距曲线，因此，可以通过坐标转换求得摆线轮齿廓方程。针齿分布圆半径为rp，滚针半径为rrp，偏心距为a，摆线轮和针轮齿数分别为Zc和Zp。点A 在坐标系XpOpYp的位置向量为：

坐标系XpOpYp到X0O0Y0的转换矩阵Mcp为：

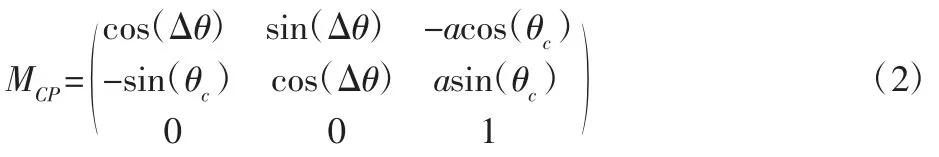
则点A 在动坐标系XcOcYc中形成的短幅外摆线为：

将式（1）～式（2）代入上式，即可得到：

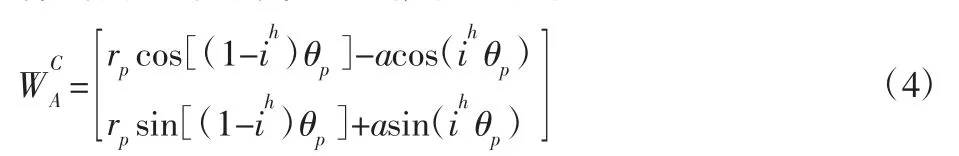
式中：ih=Zp/Zc—摆线轮与针轮的传动比摆线轮齿廓曲线Wc 的单位法向量nc：

式中：K=a*Zp/rp—短幅系数

即可得到摆线齿廓曲线的短幅外摆线的等距曲线：

3 摆线轮齿廓曲率相关公式计算

3.1 曲率和曲率半径

摆线轮齿廓是短幅外摆线的等距曲线，参数选取不合理会影响到齿廓形状进而影响到RV 减速器的传动性能。根据曲线曲率半径的基本定义可得摆线理论齿廓在任意一点处的曲率半径为：

将式（4）中对应的 x、y 分别对 θp求导，为了计算方便，令 θp=ψ 代入上述公式，可得到短幅外摆线的曲率半径为：

实际齿廓曲线的曲率半径为：

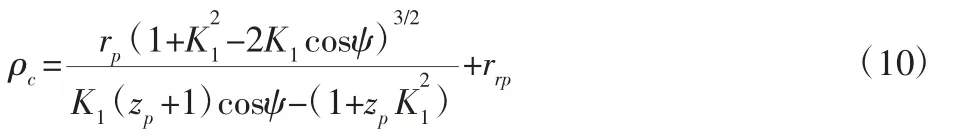
根据曲率半径与曲率的数学关K=1/p 可以得到曲率的表达式：

3.2 摆线轮诱导法曲率

诱导法曲率是啮合理论的重要内容，是研究两个相切曲面相对弯曲程度的量，是决定该传动装置润滑条件好坏和接触强度大小的重要因素[13]。计算曲面的诱导法曲率可以为评价新型传动装置，选择最佳参数组合及探索新型传动装置提供理论依据[14]。

对于摆线轮与针轮的啮合，由于针轮半径为定值，所以沿切线方向的法曲率为kn2=1/rp，摆线轮沿切线方向的法曲率为kn1。

在任意凸区间接触点处摆线针轮啮合的诱导法曲率：

在任意凹区间接触点处摆线针轮啮合的诱导法曲率：

3.3 齿廓曲线拐点

拐点是曲线二阶导数为0 的点，是曲线凹凸特性改变的临界点，因此在研究各参数对曲率的影响之前对拐点所在位置的研究很有必要性。

一般情况下，曲率半径和曲率都为正数，对于分析曲线的拐点特性，最好不要取绝对值，以便于区分摆线的凹凸变化。摆线轮齿廓一个轮齿的曲率半径随曲柄转角ψ 的变化，如图2 所示。

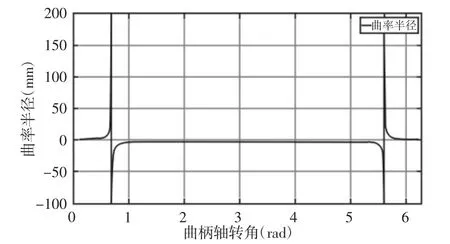
图2 齿廓曲线曲率半径Fig.2 Curvature Radius of Tooth Profile Curve

齿廓曲线曲率，如图3 所示。

图3 齿廓曲线曲率Fig.3 Curvature of Tooth Profile Curve

结合图3 对式（11）分析，曲线凹凸特性发生改变对应的曲柄轴转角：

将曲率式（11）对曲柄轴转角ψ 求导，则曲线曲率在极值处对应的曲柄轴转角：

4 摆线齿廓特性分析

摆线针轮传动是少齿差传动的一种，RV 减速器主要应用一齿差，用途并不广泛，但是随着工业的快速发展，机器人需求量开始逐渐增大，RV 减速器型号也开始增多，参数化设计就显得至关重要[15]。所以有必要将摆线轮参数对摆线轮齿廓曲线曲率的影响进行分析。

以本实验RV-20E 减速器为研究对象，各数据为：针齿分布圆半径rp=52.5mm，偏心距a=1mm，针轮半径rrp=1.25mm，针齿数Zp=40，ih=40/39。

表1 RV-20E 减速器主要参数Tab.1 The Main Parameters of RV-20E Reducer

4.1 摆线齿廓曲线的拐点位置变化情况

由图2 可知，曲柄轴转角在［0，π/2］区间和［π/2，π］区间曲率半径呈对称分布，分别存在曲率半径突变的点。根据曲率半径与曲率的数学关系k=1/p，可知在该点曲率应为0。为了形象描述其变化规律，作出曲率与曲柄轴转角的图3 便于对拐点位置进行分析。

当曲线曲率半径>0 时，曲线内凹，曲率半径<0 时，曲线外凸。在曲线由内凹到外凸的变化中会出现拐点，由曲率图（3）可知，在区间［0，2π］，曲率曲线在两个位置曲率为0，存在对称拐点。因此，求出k=0 所对应的曲柄轴转角，即可求出拐点位置同摆线轮齿廓参数的关系。由式（14）求得的拐点位置对应的曲柄轴转角公式，影响拐点位置的参数有偏心距a、针齿分布圆半径rp和针齿数Zp。

4.1.1 偏心距对拐点的影响

偏心距对拐点位置的影响，如图4 所示。偏心距对拐点的位置影响很大，偏心距在（0.2～1）mm 之间，拐点坐标位置以抛物线形式减小，偏心距大于1mm 后，拐点坐标位置以近似指数形式减小，逐渐向齿根方向靠近。总的来说，随着偏心距的增大，拐点位置不断向齿根移动，从而会增强齿根位置的传动性能。

图4 偏心距对拐点位置的影响Fig.4 The Effect of Eccentricity on the Position of the Inflection Point

4.1.2 针齿数Zp对拐点的影响

齿数对拐点位置的影响，如图5 所示。

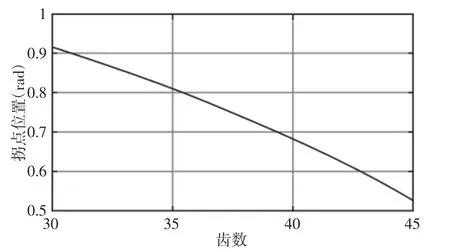
图5 齿数对拐点位置的影响Fig.5 The Effect of the Number of Teeth on the Inflection Point

在摆线针轮行星机构中，摆线轮与针齿一般相差一个针齿。针齿数影响着摆线齿廓曲线的拐点位置的移动。由仿真的图5，拐点坐标位置随着齿数的增加，以接近一次函数形式递减，逐渐向齿根方向靠近。因此，在设计摆线针轮减速器时，需要综合考虑摆线轮齿数与摆线轮齿廓曲线拐点位置的关系，在良好的传动性能条件下，选择合适的针齿数以保证不同条件下对传动性能的要求。

4.1.3 针齿分布圆半径rp对拐点位置的影响

针齿分布圆半径对拐点位置的影响，如图6 所示。不同于针齿数Zp和针齿分布圆半径rp对曲线拐点的影响，由仿真得出的结果分析，随着针齿分布圆半径增大，拐点坐标位置以近似二次抛物线逐渐增大，逐渐远离齿根，其中，针齿圆半径在区间（45～50）mm，拐点位置变化迅速，在（45～60）mm 之间变化缓慢。增大针齿分布圆半径，有利于增强齿顶方向的传动性能。

图6 针齿分布圆半径对拐点位置的影响Fig.6 The Effect of Circular Radius on Inflection Point

4.2 摆线齿廓的曲率在凹凸区间的变化规律

MATLAB 仿真出实际齿廓曲线的曲率随曲柄轴转角的变化图像，如图3 所示。在［0，ψ1］区间内，为凹区间，曲率为正，曲率的最大值在曲柄轴转角为0 时刻，带入曲率公式（11），得出最大曲率Kmax=0.7412，此时对应的最小曲率半径为pmin=1.3510。最小曲率为0，对应曲柄轴转角为ψ1。在［ψ1，π］区间内，为凸区间，曲率最小值在曲柄轴转角为ψ2时刻，代入本实验室RV 减速器参数最小曲率为Kmin=-0.3386。

4.3 各因素对曲率变化快慢的影响

摆线针轮传动是一种新型传动，它的一个很重要的参数就是齿廓曲率，对齿廓曲率的分析有利于摆线轮修形和计算轮齿接触力，因此研究曲率的变化有利于提高摆线针轮传动效率。

4.3.1 偏心距对曲率的影响

图7 偏心距对曲率的影响Fig.7 The Effect of Eccentricity on Curvature

偏心距对曲率的影响，如图7 所示。对应相同的曲柄轴转角，曲率最小值随着偏心距的增大而减小，曲率的最大值随偏心距a 的增大而增大。曲率在齿根附近变化迅速，在齿顶附件曲率变化平缓，随着偏心距a 的增大，曲率在齿根附件变化越来越迅速，在齿顶附件齿廓曲线的曲率随着偏心距a 的增大波动逐渐加大。

4.3.2 针齿分布圆半径对曲率的影响

针齿分布圆半径对曲率的影响，如图8 所示。对应相同的曲柄轴转角，由图8 分析，针齿分布圆半径的增大使摆线轮齿廓曲率的最小值和最大值随之变大；同时，针齿分布圆半径的增大，拐点所在位置逐渐向齿顶方向靠近，曲率的变化在靠近齿根方向开始减缓，曲率大小在齿顶方向变大，但在齿顶方向曲率的波动基本保持不变。

图8 针齿分布圆半径对曲率的影响Fig.8 The Effect of Circular Radius on Curvature of Needle Teeth

4.3.3 针齿半径对曲率的影响

针齿半径对曲率的影响，如图9 所示。由图9 分析，曲柄轴转角相同，曲率最小值随着针齿半径rrp的改变基本保持不变，曲率的最大值随着针齿半径的增大先保持减小最后趋于不变。增大针齿半径，不会影响齿廓曲线拐点所在的位置，曲线的曲率在齿顶方向的波动也不受影响，但是，随着针齿半径的增大，曲线的曲率在齿根方向的波动会逐渐减缓。

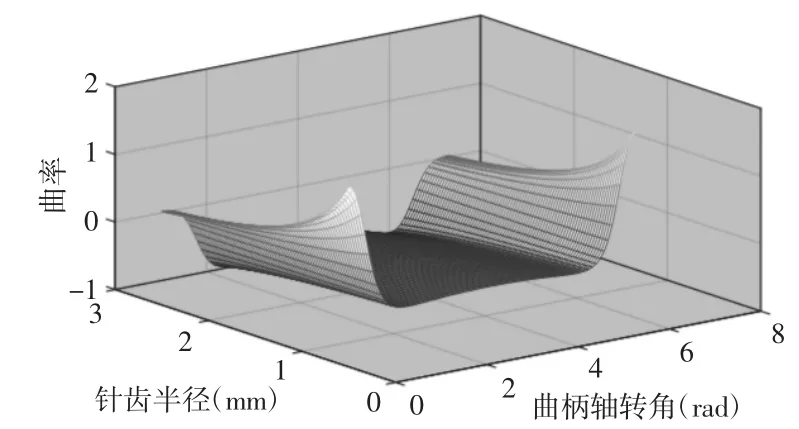
图9 针齿半径对曲率的影响Fig.9 The Effect of the Radius of the Needle on the Curvature

5 结论

（1）基于齿轮啮合原理的方法对摆线针轮传动进行了分析，推导出了摆线齿廓曲率公式和摆线轮与针轮啮合的诱导法曲率公式。

（2）摆线轮齿廓在齿根到齿顶区域分别存在一个对称拐点。

（3）摆线轮齿廓曲率在齿根附近变化迅速，在齿顶附近变化平缓，在内凹的齿廓区间，曲率的最大值在齿根处，最大值为0.7412；在外凸的齿廓区间，曲率的最小值并不在齿顶，而在曲柄轴转角为ψ2处，对应的最小值为（-0.3386）。

（4）摆线轮偏心距a、针齿分布圆半径rp的改变都会影响齿廓曲率的波动，增大摆线轮偏心距a 或减小针齿分布圆半径rp会使摆线轮齿廓的拐点所在位置向齿根方向靠近，这与前面分析的影响拐点参数的结果相吻合，说明了分析的准确性。因此在设计摆线轮时，减小偏心距a 或增大针齿分布圆半径rp均有利于改善摆线轮齿廓在齿顶方向的传动性能。另一方面，针齿半径的改变不会影响摆线轮齿廓曲率在齿顶方向的波动，也不改变摆线轮齿廓曲线的拐点位置。

（5）通过分析摆线轮各参数对摆线轮齿廓曲线拐点位置和齿廓曲率的影响，对摆线齿廓修形和分析摆线针轮的传动提供理论帮助。