轮式移动机器人路径跟踪控制方法研究

肖献强，程亚兵，王家恩，王鼎用

（1.合肥工业大学机械工程学院，安徽 合肥 230009；2.合肥工业大学 汽车与交通工程学院，安徽 合肥 230009）

1 引言

随着工业制造自动化和智能化水平的不断提高，移动机器人已经成为工业智能制造领域不可或缺的智能化设备，以取代传统工业制造中繁重的人工劳动[1-3]。移动机器人的路径规划和路径跟踪是实现自主移动的基础[4-5]。路径跟踪控制是通过控制模型及方法使移动机器人不断逼近并最终到达规划的目标位置。路径跟踪控制作为移动机器人研究的一个关键技术，是在满足一定的安全性和稳定性的前提下，通过控制移动机器人的速度和移动方向，不断缩小运动过程中的偏差，最终实现路径跟踪。近年来，许多学者对路径跟踪控制方法进行了深入的研究[6-10]。早期研究人员在经典PID 控制的基础上，提出了前馈加PID 反馈的非线性PID 控制的方法[6-7]，为了提高PID 控制的鲁棒性，具有学习功能的自适应[8]、预瞄控制[9]、模糊控制[10]等优化PID 算法被提出。PID控制虽能解决移动机器人的路径跟踪问题，但是PID 控制参数的获取需要通过大量标定，难以实现最优控制。针对以上问题，同时为了减少道路曲率、预瞄距离等对路径跟踪控制精度的影响，提出一种基于动态预瞄的移动机器人路径跟踪控制方法，根据目标点坐标与方向角度求解路径跟踪直线方程，并在该直线上选取合适的预瞄点，分析移动机器人当前位置与预瞄点在局部坐标系下的位置关系，建立路径跟踪偏差模型，结合路径跟踪偏差模型在移动机器人与预瞄点之间实时动态规划虚拟路径，从而获取由当前位置到达目标点的期望横摆角速度，最终实现精确的路径跟踪控制。

2 路径跟踪控制方法

移动机器人的循迹控制主要包括路径规划和路径跟踪控制两个方面内容。此处研究的重点为路径跟踪控制方法，即在通过路径规划方法获得期望运动路径后，控制移动机器人实现对该期望运动路径的跟踪。

移动机器人控制系统由地图构建与定位、路径规划、路径跟踪以及底层控制四个模块组成。地图构建与定位模块构建移动机器人运行的全局坐标系，并完成实时定位；根据构建的地图进行路径规划，获取期望运动路径；综合移动机器人的实时位置信息以及期望运动路径，进行路径跟踪控制，计算在当前位置跟踪期望运动路径所需的期望横摆角速度，将期望横摆角速度转换为电机脉冲输出，最终实现移动机器人的路径跟踪控制。

2.1 差速轮式移动机器人运动学模型

假定在理想条件下差速轮式移动机器人在运动过程中的位姿可表示为P=［x，y，φ］T，其中x 表示移动机器人质心相对于绝对坐标系原点X 轴方向的距离，y 表示相对于绝对坐标系原点Y 轴方向的距离，φ 表示左右轮中垂线与Y 轴的夹角。

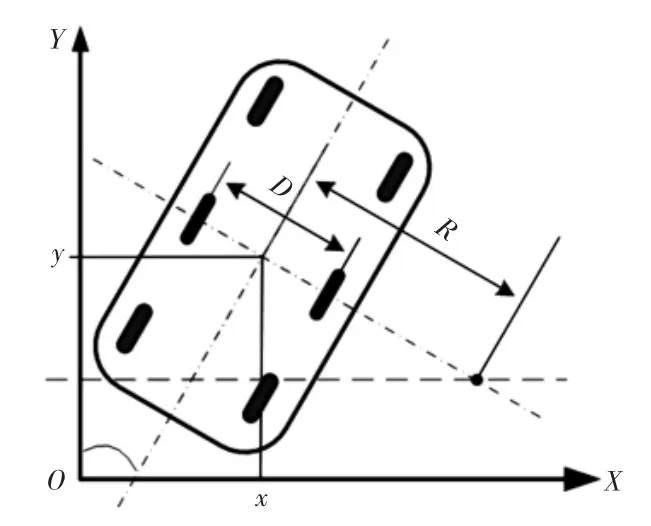
图1 运动学模型示意图Fig.1 Schematic Diagram of Kinematic Model

差速轮式移动机器人运动学模型，如图1 所示。右轮速度vr，左轮速度vl，移动机器人在移动过程中的运动状态矩阵［vx，vy，ω］T，如式（1）所示。

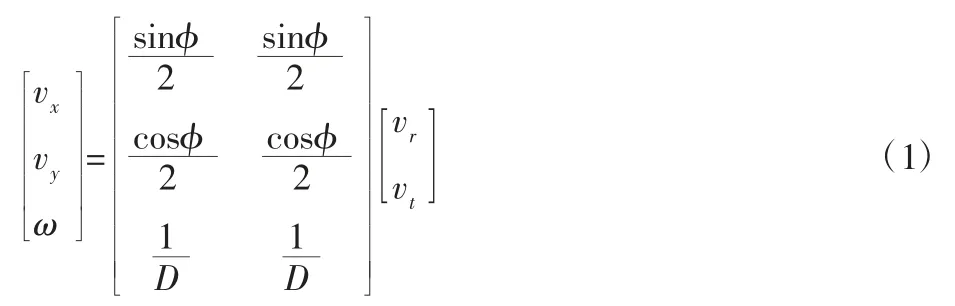
式中：vx、vy—速度在X 轴和Y 轴方向上的分量；ω—横摆角速度；D—两轮间距。

规定初始位姿 P=［x，y，φ］T=［x0，y0，φ0］T，得到任意时刻位姿矩阵与左右轮速度之间的变换式（2）。

2.2 路径跟踪偏差模型

移动机器人在路径跟踪控制中的偏差模型包括四个部分：路径跟踪直线方程求解、预备目标点计算、预瞄点选取以及偏差计算。

移动机器人由当前点到达目标点，当前点用带方向的蓝色圆点表示，目标点用带方向的红色表示，黄色圆点表示预备目标点，绿色圆点表示预瞄点，如图2 所示。根据目标点坐标及方向角度求解路径跟踪直线方程，并根据预备目标点到目标点距离Δl和预瞄距离Δd 确定路径跟踪预备目标点和预瞄点。最后计算移动机器人当前位置相对于预瞄点的纵向、侧向以及方向偏差。

图2 路径跟踪偏差模型Fig.2 Deviation Model of Path Tracking

结合目标点坐标及方向角度（xt，yt，φt）解得路径跟踪直线方程，以目标点为圆心Δl 为半径画圆弧，圆弧与路径跟踪直线存在两个交点，如图2 所示。根据目标点的方向角度选取的黄色圆点作为预备目标点（x′t，y′t，φ′t），预备目标点的坐标（x′t，y′t）可根据式（3）进行求解，且有，φ′t=φt。

式中：a、b、c—直线方程的参数；移动机器人在路径跟踪控制过程中始终以当前位置为圆心Δd 为半径画圆弧，如图2 中所示绿色圆弧。当所画圆弧与路径跟踪直线相交（交点坐标的计算可参考式（3）），且交点与目标点间距离小于Δl 时，选取该交点作为预瞄点，否则始终以预备目标点作为路径跟踪控制的预瞄点（xp，yp，φp）。

移动机器人当前位置相对于预瞄点的偏差即为预瞄点在以当前位置为原点的局部坐标系下的坐标，如式（4）所示。

2.3 路径跟踪控制方法设计

在OcXcYc局部坐标系中移动机器人质心与预瞄点之间实时构造虚拟路径[9]，如图3 所示。

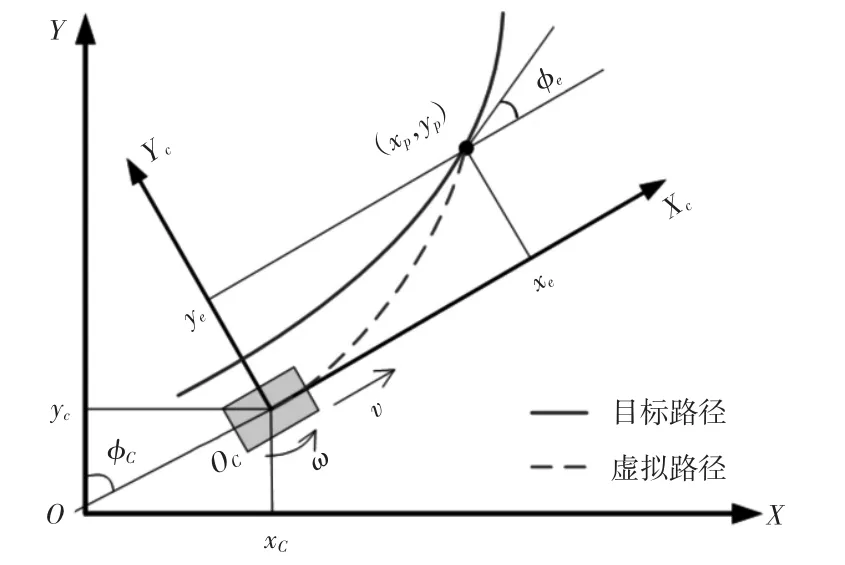
图3 路径跟踪控制方法示意图Fig.3 Schematic Diagram of Path Tracking Control Method

假设该虚拟路径方程，如式（5）所示。

式中：A、B、C、D、E、F—虚拟路径方程的参数。

局部坐标系OcXcYc是以移动机器人当前位置为原点，当前方向为X 轴正方向建立的，如图3 所示。在局部坐标系下虚拟路径的构造条件为：起始点坐标为（0，0），斜率为 0，曲率为 ρ=ω/v；预瞄点坐标为（xe，ye），斜率为tanφe，曲率为0。根据构造条件即可求解得虚拟路径方程为：

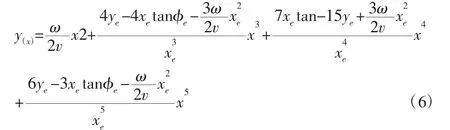
已知虚拟路径的曲线方程为y（x），移动机器人质心在曲线上的坐标为（x，y），速度为v，速度方向及运动曲率与移动机器人当前所在曲线上点一致。定义ωd为运动轨迹为曲线方程时的理想横摆角速度，其计算公式，如式（7）所示。则理想横摆角速度变化率的计算公式，如式（8）所示。

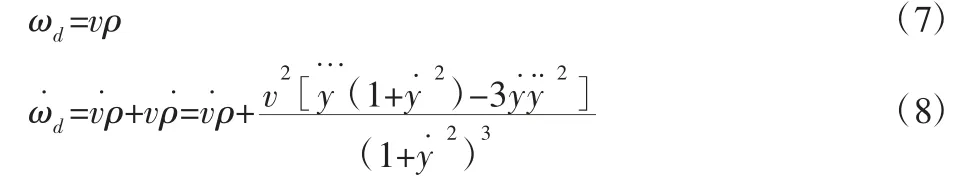
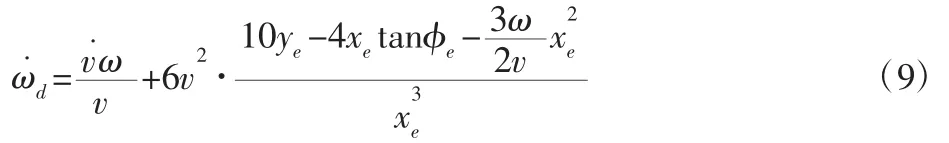
期望横摆角速度ωc为当前横摆角速度加上理想横摆变化率与采样时间的乘积，如式（10）所示。

3 实验验证

3.1 实验平台介绍

实验平台采用自主设计的差速轮式移动机器人，其基本参数，如表1 所示。

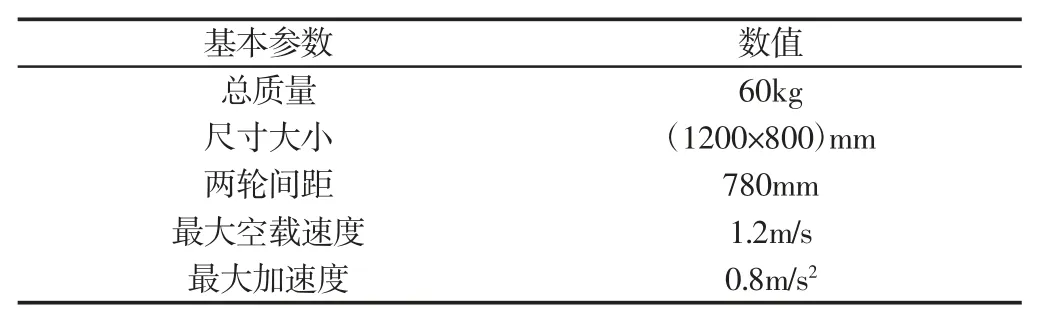
表1 差速轮式移动机器人基本参数Tab.1 Basic Parameters of Differential Wheeled Mobile Robots

3.2 实验数据分析

移动机器人的实验运动路径为8 字形，移动机器人需要进行连续的圆弧转向以充分验证所设计的移动机器人路径跟踪控制方法的可靠性、稳定性和精确性，以左下角站点为起始点，运动轨迹为①-②-③-④最终到达终点，如图4 所示。

移动机器人实验过程中的实际运动轨迹曲线图，如图5 所示。从轨迹曲线图中可以看出移动机器人能很好的跟踪规划的运动轨迹。对比图4 与图5，实际运动轨迹与期望运动轨迹非常接近，表明了设计的路径跟踪控制方法的精确性和可靠性。

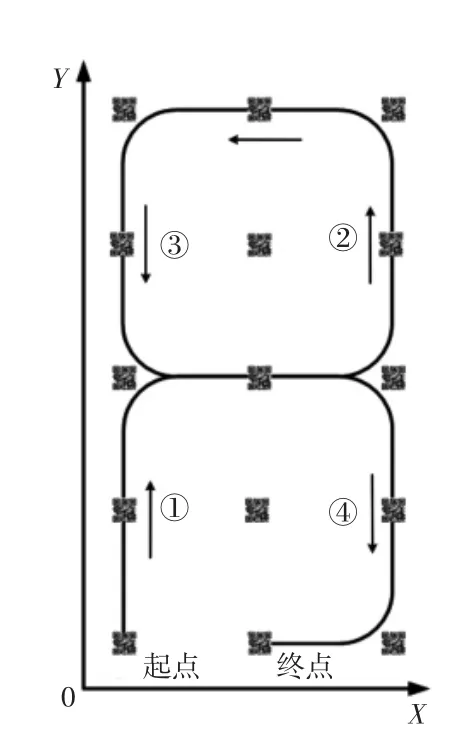
图4 期望运动轨迹曲线Fig.4 Desired Trajectory Curve

图5 实际运动轨迹曲线Fig.5 Actual Trajectory Curve

移动机器人在运动过程中侧向偏差和横摆角速度的变化曲线，如图6 所示。进行圆弧转向时横摆角速度变大，结束转向时横摆角速度恢复至正常值。从横摆角速度变化曲线可知，横摆角速度始终保持在±0.6rad/之间，并且在整个运动过程中横摆角速度的变化曲线非常光滑，表明移动机器人在路径跟踪控制过程中运动平缓，可靠。当移动机器人运动至地标位置时，利用地标对惯性导航过程中的累积误差进行消除，故在图6 中会出现侧向偏差发生突变的现象。从图中可以看到在运动过程中惯导的累积误差能够保证在±6mm，表明该路径跟踪控制方法能够实现高精度的路径跟踪控制。

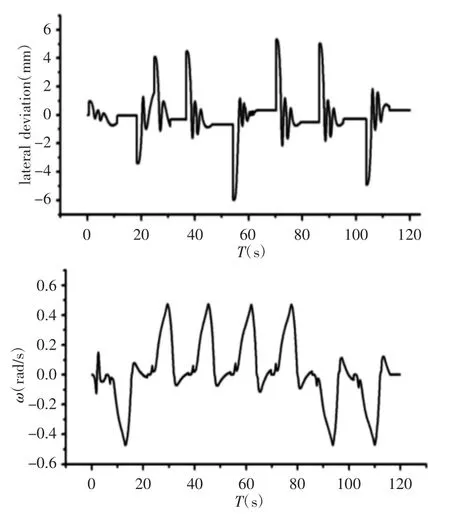
图6 侧向偏差及横摆角速度变化曲线Fig.6 Variation Curve of Lateral Deviation and Yaw Rate

4 结论

（1）根据移动机器人的运动状态及其路径跟踪预瞄点在局部坐标系中的相对位置，在移动机器人质心和预瞄点之间实时规划出一条逼近目标轨迹的动态虚拟路径。

（2）针对传统的基于PID 的路径跟踪控制方法参数标定困难的问题，研究设计了一种基于预瞄点的移动机器人路径跟踪控制方法，并进行了实验测试，结果表明本方法能够实现高精度路径跟踪控制，可实现6mm 控制精度。

（3）移动机器人在运动过程中仍然存在一定的误差，其中误差的主要来源包括传感器误差，机械结构导致的误差等，在之后的研究中应采取措施避免此类误差，以更好的验证算法本身的精确性。