双重公差原则同轴度误差评定的不确定度研究

孙永厚，杨盛宇，唐哲敏，黄美发

（桂林电子科技大学机电工程学院，广西 桂林 541004）

1 引言

新一代 GPS（Geometrical Product Specifications）“产品几何技术规范”是实现数字化制造和发展先进制造技术的关键。新一代GPS 体系[1]中，不确定度理论的研究不再只局限于测量不确定度（方法不确定度和执行不确定度统称为测量不确定度），而进一步拓展到依从不确定度。依从不确定度包括规范不确定度和测量不确定度。

目前，国家标准已经对旧的GPS 标准[2-3]进行了修订和补充，国内外的相关学者也进行了大量的不确定度研究。2009 年文献[4]通过实例给出了PUMA 法和GUM 法的比较，得到以PUMA 法作为最佳测量程序，利用不确定度传递规律来评定测量不确定度。虽然优化了测量方法，但不确定度的评定过程仍然很复杂。同一年，文献[5]在新一代GPS 的现状和标准中指出新一代GPS 不确定度理论应该是基于数学的理论。规范和检验提供一致的产品几何描述时，可用以消除规范不确定度和方法不确定度，但只是在概念上的分析。2012 年文献[6]用传统的GUM 法和蒙特卡洛MCM 法评定平面度误差的测量不确定度，结果表明基于MCM 的不确定定度评定方法相对于GUM 法算法简单、灵活、效率高且更精确。但总的来说，上述文献还只是停留在测量不确定度研究上，很少涉及到依从不确定度的评定。

近年来，文献[7]对依从不确定度进行了研究，并给出了带有圆度误差零件的规范不确定度、方法不确定度和依从不确定度等评定方法。但该评定方法一般只局限于带有简单形状误差的零件，而对于带有双重公差原则形位误差的零件，并不适用。

公差原则是处理尺寸公差与形位公差之间关系的原则。使用不同的公差原则，可以满足不同的功能需求。例如几何公差及其基准同时应用最大实体要求（MMR）时，可使零件在满足可装配性情况下降低其加工成本[8]。

因此，本团队研究了基于双重公差原则同轴度误差的评定方法[9]，提出了用极限当量直径与相应的边界尺寸比较判断零件的合格性。但该评定方法不确定度的产生和传递是一个复杂的问题，很难直接用现有的方法分析其不确定度，故提出把极限当量直径作为不确定度评定的关键依据。通过对规范不确定度定义的理解，找到其组成因素，并得到对应的规范不确定度分量，对各分量进行合成，得到规范不确定度。正交试验优化了测量方法，使得方法不确定度的评定更准确。通过对不确定度黑箱模型中各组成因素的分析，评定执行不确定度。最后将三种不确定度合成为依从不确定度。

2 双重公差原则同轴度误差评定方法

2.1 双重公差原则同轴度误差评定方法简介

双重公差原则同轴度公差的标注，如图1 所示。

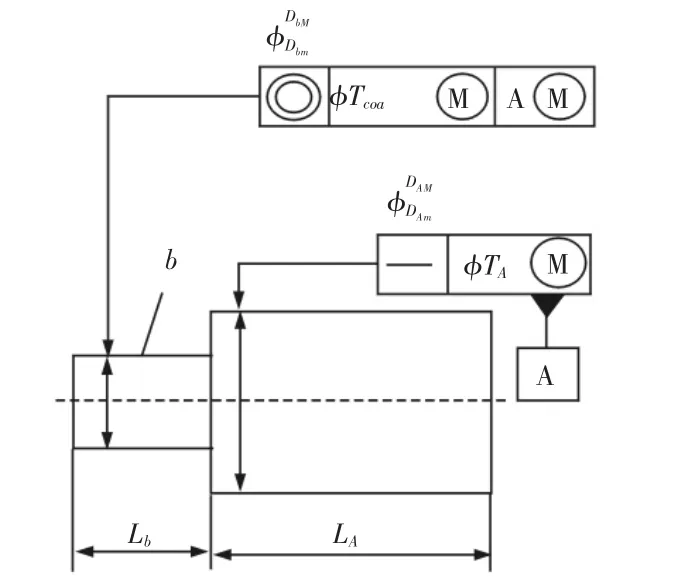
图1 双重公差原则同轴度的公差标注Fig.1 Marking of Coaxiality Tolerances

双重公差原则同轴度公差规定：至少由被测部分b 和基准部分A 两部分组成。局部尺寸分别介于各自的最大实体尺寸DbM（DAM）和最小实体尺寸Dbm（DAm）之间。基准部分A 的轴线有（直线度）形状公差TA，当基准轴线处于最大实体状态时，被测部分轴线与基准轴线有同轴度公差Tcoa。

满足上述规定的零件，可基于双重公差原则同轴度误差的评定方法评定零件是否合格。其中，评定的关键是求解被测圆柱体的极限当量直径，如果被测圆柱体的极限当量直径能够被相应的最大实体实效边界MMVBb包容，则零件符合给定的双重公差原则同轴度公差，否则零件不合格，如图2 所示。

2.2 实际被测圆柱体的极限当量直径

实际被测圆柱体的极限当量直径是指：对轴而言，当基准圆柱体A 的最大实体实效边界MMVBA（MMVBA的直径DvA=DAM+TA）包容实际基准圆柱体时，以MMVBA的轴线为轴线的、能包容实际被测圆柱体的理想圆柱的最小直径，如图2 所示。

求解被测零件的极限当量直径前，先获取在局部坐标系下，零件的基准圆柱体和被测圆柱体的测点数据 PA，n和 Pb，m。其中，PA，n=（xA，n，yA，n，zA，n）T；当 MMVBA包容实际基准圆柱体时，通过移动实际被测零件得到最小的当量直径（deq），即实际被测圆柱体的极限当量直径（deq，m），如图2 所示。

图2 实际零件M-M 同轴度的评定Fig.2 Verification of M-M Coaxiality of Actual Parts

实际零件测点的移动过程可以用目标优化问题，最终求得被测圆柱体的极限当量直径，如下：

式中：优化问题的最优解deq，m—实际基准圆柱体的极限当量直径；Pm—被测圆柱体上的点第三次移动后在局部坐标系中的坐标值；nVA，L—轴线方向向量在局部坐标系中的坐标，为了便于理解和计算，轴线方向向量在局部坐标系中的坐标nVA，L=（0，0，1）；Pb，m—被测圆柱体上的点第二次移动后在局部坐标系中的坐标值；PA，n—基准圆柱体上的点第二次移动后在局部坐标系中的坐标值；R（dα，dβ）—旋转矩阵；DvA—基准圆柱体A 的最大实体实效边界MMVBA的直径；（dx，dy，0）—实际基准圆柱微小平移向量；dα—实际基准圆柱体绕局部坐标系x 轴的微小旋转弧度；dβ—实际基准圆柱体绕局部坐标系y 轴的微小旋转弧度；LA—基准圆柱体的名义长度。

双重公差原则同轴度误差评定方法的详细推导过程可参考本研究团队唐哲敏师兄的相关研究[9]，在这里不复赘述。

3 正交试验

正交试验设计是针对复杂多因素多水平的试验，用部分试验代替整体试验，通过对部分试验分析进行寻优的一种设计方法。

在进行正交试验前，首先要通过三坐标测量机（简称CMM）获取实际被测零件的测点数据。使用扫描式CMM 进行测量时，需要考虑扫描式CMM 的工作原理。如扫描式CMM 在提取孔轴类零件内外圆柱面的数据点时，根据其工作原理即扫描路径，必须考虑扫描角度A、光条方向间隔B 以及扫描间隔C 等至少3 个因素对于测量的影响。

（1）扫描间隔A：光条与光条之间的横向间隔。

（2）光条方向间隔B：光条与光条之间的纵向间隔。

（3）扫描角度C：几个角度可以扫描完整的圆柱面。

通过正交试验的设计找到显著的影响因素，首先确认试验目的（试验指标），然后按照显著影响因素的测量方法进行多组重复试验得到结果均值。编制正交试验方案前准备如下：

①确定试验指标：这里孔轴类零件的极限当量直径。

②选因素定水平：影响因素是扫描式CMM 的扫描角度、扫描间隔和光条方向间隔。

③选择合适的表头：根据扫描式CMM 的说明手册，A、B 因素的3 个水平，如表1 所示。C 因素根据个人经验通常至少需要3个扫描角度扫描完整的孔轴类零件。

表1 表头设计Tab.1 Orthogonal Table

正交试验作为评定的关键测量策略贯穿了依从不确定度的整个评定过程，并为规范不确定度、执行不确定度和方法不确定度的评定提供了可靠的数据和更优化的测量方法。

4 依从不确定度

在国家标准[10]和新一代GPS 标准理论与应用[1]中给出新一代GPS 不确定度的组成，依从不确定度在测量不确定度基础上增加了规范不确定度，使得规范的图纸、合理的检测方法和准确的测量设备对产品的合格性都会有一定影响。

4.1 规范不确定度

规范不确定度是指实际要素/要素的实际规范操作集内在的不确定度。

对于同一种规范，由于不同的检测人员有不同的选择，所以产生了n 种选择。当选择较多时，可根据贝塞尔公式法（2）、（3）公式求得同一规范下的规范不确定度。

式中：xs—同一规范下第s 种选择测量结果的均值；us—以标准差形式表示的规范不确定度。

对于选择较少时，规范不确定度采用极差法评定：

对于多种不同规范引起的规范不确定度，我们可以把它看作是一个黑箱模型，因此规范不确定度可简单表示为：

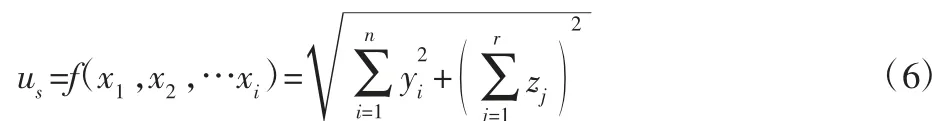
式中：xi—基于黑箱模型的不确定度影响因素；yi—无关联的规范不确定度影响因子；zi—有关联的规范不确定度影响因子。在整个评定过程中包含了分离、提取、滤波和拟合等操作。规范不确定度来源于不同的检测人员有不同的提取、滤波和拟合规范而产生的不确定度。

提取规范：正交试验中所涉及的3 因素3 水平试验共有33组提取数据。为了避免试验的复杂和重复性以及其它规范算子的影响，选取3 个影响因素中的角度因素作为提取规范的影响因素。规范不确定度来源于不同的检测人员可以选择不同的角度，把最小外接圆柱拟合（减少优化问题的形式，降低编程成本）作为除考虑拟合规范对结果影响外唯一的拟合规范，以消除拟合规范对提取规范的影响避免重复考虑。

拟合规范：基准圆柱体的拟合通常采用最小区域法、最小外接法以及最大内接等方法。基于相同的提取规范下对基准的拟合方法不同也会造成计算得到被测圆柱体的极限当量直径不同。

滤波规范：根据实验室现有的实际情况，选择上海研润光机科技有限公司的圆柱度仪MC012-DY 作为滤波仪器。滤波的频率UPR 根据评定基圆直径与触针针尖半径之比以及测点数等条件选择，不同频率的滤波条件会直接影响到在相同提取和拟合规范下基准和被测圆柱体的外圆柱面测点，进而影响到被测圆柱体的极限当量直径。

这3 种规范之间并没有直接联系，它们是不相关的。因此不同规范下的规范不确定度数学模型（6）可以进一步简化，如式（7）所示。

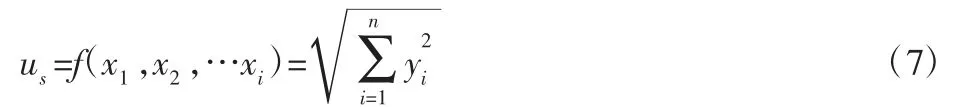
根据实际情况选择影响因素，共考虑到3 种规范不同引起的规范不确定度，如式（8）所示。

4.2 方法不确定度

方法不确定度是由实际规范操作集和实际检验操作集之间的差异产生的不确定度。

图纸上的规范可能是不明确的，检测人员根据图纸选择制定完整的规范，但由于实际检测条件限制，只能选择符合条件的检验操作，因此选择了与理想检验方法近似的实际检验方法，这两种方法之间的偏离就产生了方法不确定度。

主要是正交试验选优得到最佳的测量方法并结合高于实际测量仪器精度的“理想测量仪器”（圆柱度仪）来达到忽略测量仪器的计量特性的目的。针对不同的方法得到的测量结果均值可以估计方法不确定度umt。

4.3 执行不确定度

执行不确定度（测量仪器的测量不确定度）是由实际检验中测量仪器的计量特性偏离理想计量特性而产生的不确定度。目前，执行不确定度来源的主要影响因素：测量的仪器、测量的环境、测量的人员、测量的方法等，采用灵敏度分析和误差源分析法评定执行不确定度，过程复杂。基于不确定度评定的黑箱模型来评定执行不确定度。主要针对仪器的计量特性（示值误差、分辨力等因素）以及重复性、复现性等特性进行分析。

4.3.1 示值误差引入的不确定度

最大允许误差MPE 通常由检定证书或者试验标定得到，根据检验规范为了得到示值误差引入不确定度的合理估计，采用试验标定的方法。

实验中用到了扫描式CMM 和圆柱度仪2 种测量仪器，因此实验最大允许误差来自2 个测量设备在常规测量时，测量结果的最大差值。

示值误差引入的不确定度uE=MPE·b。式中：b—误差限。

4.3.2 分辨力引入的不确定度

测量系统的分辨力是系统固有的，因此，分辨力引入的不确定度=a2/12，式中：a—系统的分辨力。

4.3.3 重复性引入的不确定度

同一个操作人员、在同一个地点、同一时间内、用同样的测量系统对同一个工件进行多组重复独立测量。重复性引入的不确定度urt由在正交试验相同影响因素（测量程序相同）下的测量结果不同引起的。

4.3.4 复现性引入的不确定度

不同的操作人员、不同的时间段、在不同的测量程序下对同一个工件进行多次重复独立测量。复现性引入的不确定度urd是由正交试验不同影响因素（测量程序不同）下的测量结果不同引起的。

4.3.5 合成执行不确定度

国家标准[11]规定，当分辨力引入的不确定度大于重复性引入的不确定度时，应用前者取代后者。

4.4 合成依从不确定度

新一代GPS 体系中，依从不确定度由规范不确定度、方法不确定度和执行不确定度共同组成，故依从不确定度uc满足：

根据现有的计量技术规范[12]，关于测量不确定度的合成和表示方法来表示依从不确定度，即依从不确定度的扩展不确定度。

式中：uc—以合成标准不确定度形式表示的依从不确定度；kc—包含概率为c 时的包含因子。标准中明确指出，常规测量中，一般kc=2。表示由Uc=kcuc（kc=2）确定的概率分布近似正态分布时的包含概率为95%。

5 实例分析

某阀芯的尺寸与几何公差规范（本节，单位为mm），如图3所示。用这里的方法对给出的双重公差原则同轴度零件进行依从不确定度评定。实验室给定的三坐标测量机为Hexagon Metrology（Qing Dao）生产的GLOBAL CLASSIC SR 07.10.07，测量精度为0.003。

表2 实际零件的三角度正交试验数据Tab.2 Three Angle Orthogonal Test Data of Actual Parts

涉及正交试验、重复实验等多组试验，一一列举数据庞大。因此只列举一组三角度的正交试验数据作为参考。

图3 某阀芯的尺寸与几何公差规范Fig.3 Dimensions and Geometric Tolerance Specification of a Spool

5.1 正交试验

根据实例的规范要求，找到试验的指标和影响因素，选取最优组合为依从不确定度评定提供试验依据。

（1）试验指标：被测圆柱体b 的极限当量直径。

（2）选因素定水平：影响因素是扫描式CMM 的扫描角度、扫描间隔和光条方向间隔。

（3）正交表的选择：存在重复试验，考虑误差列对实验的影响，因此选择L9（34）的正交表。

（4）表头设计：如表1 所示。

（5）编制试验方案：绘制3 因素3 水平的9 组试验方案，如表3 所示。

表3 试验方案Tab.3 Testing Program

（6）最优方案：最优组合为A1B1C2，分别对应表1 中的扫描间隔A 为0.5mm，光条方向间隔B 为0.5mm，扫描角度C 为4 个角度。

利用正交试验提供的可靠数据，通过matlab 编程运算得到被测圆柱体的极限当量直径。根据极限当量直径计算规范不确定定度、方法不确定度及执行不确定度。最后，合成依从不确定度。

5.2 规范不确定度

实例中，产品规范技术文件并没有指定检验规范和标准，检测人员检测时由于不完整的规范按照自己的理解选择合适的提取规范、拟合规范和滤波规范。

5.2.1 提取规范

使用扫描式CMM 分别多次重复测量提取基于正交试验中涉及的不同的提取角度下的基准和被测圆柱体A、b 的外圆柱面测点，以最小外接圆柱法拟合基准，通过matlab 编程并求解被测圆柱体b 的极限当量直径，如表4 所示。

表4 不同提取角度下的被测圆柱体极限当量直径Tab.4 Limit Equivalent Diameters of Considered Cylinders Under Different Extraction Angles

5.2.2 拟合规范

正交试验选优后，把四角度扫描规范作为提取规范。然后在四角度提取规范下使用扫描式CMM 分别多次重复测量基于不同拟合规范下的基准和被测圆柱体A、b 的外圆柱面测点，通过Matlab 编程并求解被测圆柱体b 的极限当量直径，如表5 所示。

表5 不同拟合规范下的被测圆柱体极限当量直径Tab.5 Limit Equivalent Diameters of Considered Cylinders Under Different Association Specifications

根据表5，同理可以得到不同拟合规范下的规范不确定度分量us2=20.1μm。

5.2.3 滤波规范

标准GB/T 24632.2[13]关于滤波器的选择是根据评定基圆直径与触针针尖半径之比。依据实验室现有的测量条件：上海研润光机科技有限公司的圆柱度仪MC012-DY。因此，满足要求的滤波UPR 及对应的被测圆柱体b 的极限当量直径，如表6 所示。

表6 不同滤波规范下的被测圆柱体极限当量直径Tab.6 Limit Equivalent Diameters of Considered Cylinders Under Different Filtration Specifications

根据表6，同理得到不同滤波规范下的规范不确定度分量：us3=7.6um。

5.3 方法不确定度

检测人员通过对双重公差原则同轴度评定的理解，进一步补充完整理想的检验操作集：由正交试验得到的最优方案作为测量方案、依据最小外接圆柱法拟合基准和使用频率响应为1～50upr 的圆柱度仪。根据方法不确定度的定义，找到由于方法不同造成的测量结果的实际值和理想值。实际值：扫描式CMM 对阀体A、b 段外圆柱面进行常规测量得到测点数据，通过matlab编程计算得到被测阀体b 的极限当量直径（常规测量）。理想值：1～50upr 的MC012-DY 圆柱度仪对通过正交试验选优后的测量结果进行滤波，通过matlab 编程计算得到被测阀体b 的极限当量直径（正交试验且经过滤波）。分别对阀体的基准和被测圆柱体进行9 组常规测量和正交试验选优且经过滤波测量，计算得到被测阀体b 的极限当量直径，如图4 所示。

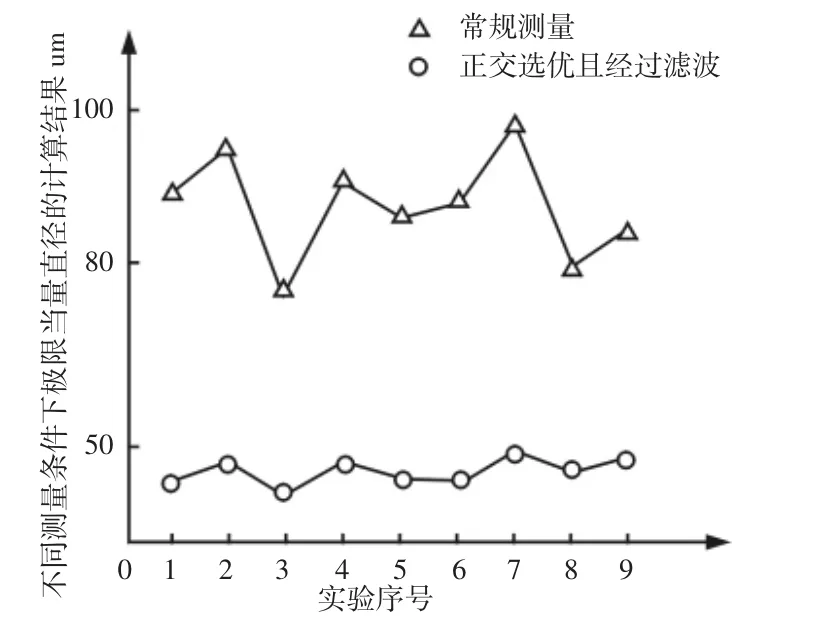
图4 不同测量条件下的被测圆柱体极限当量直径Fig.4 Limit Equivalent Diameter of Considered Cylinders Under Different Measurement Conditions

根据图4 可知，式（9）中的，则方法不确定度umt=27.8um。

5.4 执行不确定度

执行不确定度分量，如表7 所示。

表7 执行不确定度分量Tab.7 Implementation Uncertainty Component

由表7 合成执行不确定度ui=15.1um。

5.5 基于双重公差原则的依从不确定度

依从不确定度分量，如表8 所示。

表8 依从不确定度分量Tab.8 Compliance Uncertainty Component

由表8 合成依从不确定度uc=40.1μm。

由式（11）得到以扩展不确定度方式表示依从不确定度为Uc=80.2μm。

5.6 对比分析

基于相关文献[7]对依从不确定度的评定结果，如表9 所示。

由式（8）得到以扩展不确定度方式表示依从不确定度为Uc=69μm 相比5.5 节的80.2μm，依从不确定度减少了14%。这个数量级说明这里的研究方法可以更全面地分析依从不确定度的影响因素，因此是有意义的。

表9 依从不确定度分量Tab.9 Compliance Uncertainty Component

6 结论

根据规范不确定度的定义，较全面地考虑了影响因素，利用正交试验的方法，通过matlab 编程得到了方法不确定度值，与文献[7]的方法相比，正交设计优化了测量方法，使得方法不确定度更加准确。这里研究方法虽然使依从不确定度更全面更准确，却引起依从不确定度区域进一步变大。但只要保证设计规范明确且与检验者沟通一致，通过恰当的测量检验方法可以使不确定区域降到最低，提高产品检验的合格率从而减少产品的报废率，降低成本。但由于其不确定度会随着基准圆柱体的大小改变而发生不规则变化，因此将来的工作主要是通过蒙特卡洛模拟实验的方法，补充评定基于双重公差原则同轴度误差评定方法的不确定度，使得不确定度评定更加可靠。