多光谱遥感影像的两种浅海水深反演模型对比与分析
2021-01-27戚甲伟任照宇赵金秀朱金山
戚甲伟,任照宇,赵金秀,朱金山*,3
(1.地理信息工程国家重点实验室,陕西 西安 710054;2.山东科技大学 测绘科学与工程学院,山东 青岛 266590;3.自然资源部 海洋测绘技术重点实验室,山东 青岛 266590)
0 引言
水深信息对近海和海岸带规划与管理、航海和海洋环境科学研究具有重要意义。船舶航道的监测以及水下沙洲、岩石、浅滩、暗礁等海洋特征的监测都依赖于精确的水深测量[1-2]。一些近岸活动(如娱乐、渔业和水产养殖等)和近海工程(如电缆和管道铺设、疏浚、石油钻探等),也需要了解水深的分布状况。研究海洋底质分类时,可利用水深信息进行水体校正,去除水体对底质的影响从而提高底质分类的准确性。
根据光在水体中的辐射传输理论,光在水体中呈指数衰减,LYZENGA[3]给出了浅水区水深与海表辐亮度的关系。海表面的辐亮度除了与水深有关外,还与水底的底质类型以及水体本身的光学属性有关。如果底质类型单一,水深值与单波段的辐亮度存在较好的相关关系,可根据单波段来反演水深;当底质类型不单一时,需要利用多个波段来计算水深[3-4]。1985年LYZENGA[4]提出了一个双波段线性回归模型(Lyzenga 1985模型),利用多光谱数据与激光雷达数据进行了水深反演,其研究证明利用多光谱遥感数据进行水深反演是可行的。论文还讨论了水底底质的变化和水体光学属性的变化对水深反演精度的影响。
针对多种水底底质,STUMPF et al[5]提出了对数变换模型(Stumpf 2003模型),此模型建立了2个波段对数变换后的比值与水深的关系,需要根据实测水深数据来确定模型中的3个未知参数。该研究利用高分辨率的IKONOS多光谱数据和激光雷达数据进行了水深反演与验证。其研究表明,受底质影响,如果遥感影像中某些地方浅水区的海表反射率比深水区的海表反射率还要小,则不能采用线性模型反演。
本文选择Lyzenga 1985和Stumpf 2003两种模型,在南海附近水域进行水深反演比较,分析各波段与水深的相关性,使用Levenberg-Marquardt(L-M)[6-8]最小二乘回归方法求解模型参数,统计回归点与真实水深点之间的偏移量,比较不同底质情况下两种模型的反演精度。
1 研究区概况与数据处理
1.1 研究区概况
南海位于中国大陆的南方,是太平洋西部海域,为中国三大边缘海之一。研究区域位于南海西沙群岛的北岛海域(图1),水域面积约为4 km2,水深小于20 m,变化缓慢,层次性较好。研究区浅海水域海水清澈,适合利用光学方法进行浅海水深反演研究。
海岛被灌木和低地包围,四周由宽约80 m左右的白色沙堤环绕,沙堤由珊瑚、贝壳、沙屑组成。其潮坪区在高潮时被海水淹没,低潮时露出海面。
1.2 卫星数据
WorldView-2是DigitalGlobe公司的第3颗运行卫星,运行在770 km高的太阳同步轨道上,可捕获0.5 m分辨率的全色图像和1.8 m分辨率的多光谱图像,覆盖的光谱范围从400 nm到1 040 nm。本研究使用4个多光谱波段(红、绿、蓝、近红外)的数据,数据采集时间为2010年2月。整幅图像云层覆盖率约1%,研究区域内无云层影响。
1.3 实测水深数据
水深数据采用CGCS2000国家大地坐标系、Gauss-Kruger 3°带投影,基准面为当地岛礁潮高基准面,由“海南省三沙市部分岛礁周边礁盘海域水下地形测量项目”获得。测量时使用HY1601测深仪和广州南方灵锐S86型GPS接收机,将测深仪与接收机进行连接,测深仪每秒(水平点位间距约3 m)采集1个点,两者实时同步获得点位的坐标与深度,同步记录该点位潮汐高度信息。

图1 研究区域地理位置示意图Fig.1 The location of research area
1.4 卫星影像预处理
研究流程如图2所示,对WorldView-2卫星影像进行必要的几何校正、辐射校正、太阳耀斑校正以改正遥感影像几何误差,削弱太阳辐射和水面局部强反射的影响,使图像信息真实可靠[9]。
采用6S (Second Simulation of the Satellite Signal in the Solar Spectrum)数值模型进行大气校正[10],将大气顶辐亮度转换为海表辐亮度。6S模型由Fortran语言编写,根据WorldView-2的波段信息给模型添加WorldView-2的光谱响应。模型输入的参数包括:(1)几何参数,如太阳天顶角、太阳方位角、卫星天顶角、卫星方位角等;(2)大气模型,本文选用美国标准大气;(3)气溶胶类型,本文选用海洋性气溶胶;(4)地球表面反射模型,本文选用海洋的反射率模型。由于研究区北岛长度仅约1.6 km,空间跨度不大,校正时对整个研究区采用了相同的大气校正参数。

图2 研究流程图Fig.2 Flow chart of research
对于宽视场角影像来说,无法避免波浪导致的水面局部强反射(Sun Glint),特别是对空间分辨率小于10 m的遥感影像[11-12]。GOODMAN et al[13]研究表明,遥感影像中30%以上的水深反演误差都是由这种强反射造成。目前针对高分辨率卫星遥感数据的太阳耀斑校正方法主要包括HOCHBERG et al[14]提出的方法以及在此基础上改进的HEDLEY et al[11]的方法和LYZENGA et al[15]的方法。本文采用HEDLEY et al[11]的方法对WorldView-2卫星数据进行太阳耀斑校正。具体算法公式如下:
Lwb(λ)=L(λ)-b(λ)[L(NIR)-Lmin(NIR)]
(1)
其中:Lwb(λ)为采样波段耀斑校正后的像元值;L(λ)为此波段校正前的像元值;Lmin(NIR)为近红外波段的像元最低值;L(NIR)为近红外波段的像元值;b(λ)是以近红外波段为横轴,采样波段为纵轴回归出的直线的斜率。
图3为太阳耀斑校正前后的对比图(图像进行了增强处理,使噪声便于观察),校正后图像中的干扰图斑已经被改正。


图3 太阳耀斑校正前后图像(图像增强处理后)Fig.3 Before and after sun glint correction (after image enhancement)
1.5 水位校正与数据匹配
本研究采集的水深数据是以岛礁潮高基准面为基准的稳态水深,由于水深反演模型需要的是影像过境时对应的瞬时海水深度,故需进行潮汐改正得到影像的实际水深值[16]。对照2010年2月10日(卫星数据获取时间)的潮汐表(永兴潮高基准面),获取影像成像时刻的潮高为79 cm。由于潮汐表与实测水深数据的潮高基准面一致,因此,遥感影像成像时刻的实际水深值即为实测水深值与成像时刻的潮高之和。
为实现遥感影像与水深信息的配准,首先对实测数据进行投影转换,将遥感数据和实测数据统一到UTM、WGS-84投影坐标系中。再选择3个清晰、易获取的特征点作为控制点,进行精确配准。由于卫星影像的1个像元反映的是1.84 m×1.84 m范围的水深平均值,以其中1个实测点作为整个像元的水深值误差会很大,因此将其重采样为1.84 m空间分辨率,对实测序列进行统计分析,与遥感数据匹配[17]。
2 水深反演模型与方法
2.1 模型介绍
Lyzenga 1985模型[4]可表示为:
(2)
其中:a0和ai是常系数,N是参加反演的波段数量,R(λi)是波段的海表反射率,R∞(λi)是波段i对应的深水区反射率均值。可采用直方图统计的方法确定深水区像元,其原理为在浅水区由于存在水底反射,其像元值大于深水区像元,随深度加大,像元值会随之减小。因此直方图中像元值最小的部分,且远离岛屿的像元可确定为深水区像元。Lyzenga 1985模型中的自然对数变换使得水深与光谱波段辐射之间产生了一种线性关系,它是目前应用较广泛的多光谱遥感影像水深估算模型。
Lyzenga 1985模型中需要减去深水区辐亮度值,这有可能会造成进行对数变换的值为负数,进而使结果出现无理数,使得这些区域的反演为无效值。为避免这种情况,STUMPF et al[5]提出了一种基于对数变换波段比的非线性水深反演模型:
(3)
其中:m1,m0和n是常系数;R(λ2)和R(λ1)是2个波段的海表反射率。
Lyzenga 1985和Stumpf 2003两种水深反演模型都基于这样的假设:(1)水体的光学属性如衰减系数,在研究区内无空间变化,也就是说要满足在相当大的区域内水质均匀。若水质确实表现出显著的空间变化,那么模型的深度估计将会有很大的误差。(2)对于给定图像中的不同的底质类型,2个光谱波段的海底反射率之比是相同的。这一假设存在一定局限性,会对一些区域的反演精度造成影响。综上所述,我们需要从多光谱图像中提取水体清澈度高、水体水质和底质类型均匀的采样区域,以满足反演模型的假设前提。
2.2 L-M算法
L-M算法[7-8]通过最小化目标函数得到问题的最优解,可用于最小二乘问题的参数求解,也可用于非线性问题的求解。对于本研究中采用的2个模型,公式(2)中有3个未知数,可转化为求解线性方程的最小二乘问题;公式(3)中存在3个未知数,可转化为非线性方程的参数求解问题。因此,这2个模型均可采用L-M算法获得模型参数。
L-M算法中,给定参数的初始值,通过迭代更新参数,直到新的参数能够满足收敛条件(目标函数最小)。其迭代公式如下:
Pi+1=Pi+[H+λdiag(H)]-1f(Pi)
(4)
其中:Pi表示当前参数向量,Pi+1表示下一步迭代中采用的新的参数向量,H是目标函数的黑森矩阵,λ是衰减因子,f(Pi)表示目标函数值的梯度。
针对2个模型定义目标函数为:
(5)
其中:N表示建模时采用的点的个数;zi表示第i个实测水深值;zmi表示第i个由模型得到的估计水深值。当目标函数最小时,表示模型估计值与实测值最接近,此时的模型参数为最优模型参数。
2.HBO组患者治疗前后细胞免疫功能的变化:经1个疗程治疗后,HBO组患者的细胞免疫指标较治疗前均有显著改善,差异均有统计学意义(P<0.05)。见表2。
公式(5)中,根据水深反演模型的不同,zmi可由公式(2)或公式(3)得到。
L-M流程图如图4所示,首先给出模型的初始值,由初始值和反演模型[公式(2)或公式(3)]得到模型估计的水深值;根据模型值与实测值计算目标函数值[公式(5)];然后根据目标函数值判定是否达到收敛条件,如果未收敛则根据公式(4)更新模型参数,并将新的参数输入到反演模型重新估计水深值。经多次迭代直到达到收敛条件,得到最优的模型参数。

图4 L-M算法流程图Fig.4 Flow chart for the L-M algorithm
3 数据集与波段选择
3.1 采用的数据集
研究区域水深较浅,水体透明度较好,由于WorldView-2有较高的空间分辨率,根据真彩色影像(图5),研究区中存在两种明显不同的底质。图中A点标注的位置为底质较暗的区域,经现场拍摄的视频确认为珊瑚底质(底质区域A);B点所示位置底质较亮,经现场拍摄的视频确认为砂质底质(底质区域B)。

图5 研究区域划分Fig.5 Study area division
由于研究区存在两种明显不同的底质,根据底质不同建立了2组数据集。数据集每个样本包含实测水深值和WorldView-2四个波段的像元值。其中区域A共有410个样本,300个样本用于建模,110个样本用于模型的验证;区域B共125个样本, 100个样本用于建模,25个样本用于模型的验证。
3.2 波段选择
不同波长的光穿透水时,衰减程度不同,波长越长衰减越快。在清澈的水中,蓝波段(440~540 nm)的最大穿透深度约为30 m,绿波段(500~600 nm)的约为15 m,红波段(600~700 nm)的约为5 m,近红外波段(700~800 nm)的约为0.5 m[2]。透光深度受水体浑浊度的影响,悬浮沉积物、叶绿素和溶解的有机化合物增加了浑浊度,从而降低了光的穿透深度。在建立反演模型之前,将大气校正与太阳耀斑校正后所得到的每个波段的海水反射率与水深值进行相关性分析(表1),确保建立模型的波段是合理可靠的。从表中可以看出,对于单波段来说,绿波段与水深值相关性系数最高,而近红外波段由于在水中迅速衰减,其与水深数据相关性最差。选择相关性较高的蓝波段和绿波段作为模型的反演波段。

表1 各波段反射率与水深值相关系数Tab.1 Correlation coefficient between reflectivity of each band and water depth value
4 反演结果分析与比较
4.1 区域A模型相关性与残差分析
对于区域A,为了保证评估的可靠性,我们从已经建立的数据集中选择了300个样本用于建模,110个样本用于模型检验,检验点专门用于检验模型的误差,不参加建模过程。根据公式(1)~(4),对两种反演模型回归所进行的迭代过程如表2和表3所示。由表可知,迭代次数与选取的回归初始参数有关,随着迭代次数的增加,残差平方和逐渐减小并趋于稳定,模型中的参数逐渐趋向最优值。

表2 Stumpf 2003模型的回归迭代结果(区域A)Tab.2 Regression iteration results of Stumpf 2003 model(area A)
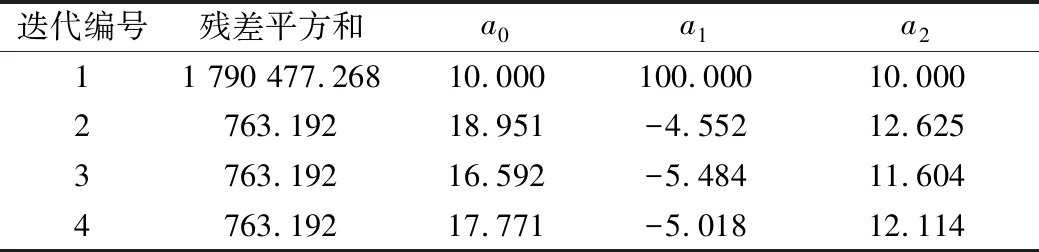
表3 Lyzenga 1985模型的回归迭代结果(区域A)Tab.3 Regression iteration results of Lyzenga 1985 model(area A)
为了比较两种模型的反演精度和优劣,将Stumpf 2003模型与Lyzenga 1985模型的结果与真实水深进行对比和分析,统计检验点水深反演值的决定系数(R2)和均方根误差(RMSE)。结果如图6和表4所示。

图6 反演水深与实测水深对比(建模数据集,区域A)Fig.6 Comparison of the retrieved depth and the in-situ depth(modeling dataset, area A)

表4 两种反演模型的误差比较(建模数据集,区域A)Tab.4 Error comparison of the two inversion models (modeling dataset, area A)
从表4可以看出Stumpf 2003模型的决定系数为0.776; Lyzenga 1985模型的为0.860,并且均方根误差也小于前者。所以在模型拟合方面,Lyzenga 1985反演模型优于Stumpf 2003模型。


图7 两种模型的回归标准化残差图 (建模数据集,区域A)Fig.7 Regression standardized residuals of the two models(modeling dataset, area A)
4.2 区域B模型相关性与残差分析
对于区域B,从数据集中选择了100个样本用于建模,25个样本用于模型检验。
迭代过程如表5和表6所示,与区域A结果类似,随着迭代次数的增加,残差平方和逐渐减小,模型中的参数逐渐趋向最优值。

表5 Stumpf 2003模型的回归迭代结果(区域B)Tab.5 Regression iteration results of Stumpf 2003 model(area B)

表6 Lyzenga 1985模型的回归迭代结果(区域B)Tab.6 Regression iteration results of Lyzenga 1985 model(area B)
将Lyzenga 1985模型与Stumpf 2003模型的结果与真实水深进行对比和分析,统计检验点水深反演值的决定系数(R2)和均方根误差(RMSE),结果如图8和表7所示。

图8 反演水深与实测水深对比(建模数据集,区域B)Fig.8 Comparison of the retrieved depth and the in-situ depth(modeling dataset, area B)

表7 两种反演模型的误差比较(建模数据集,区域B)Tab.7 Error comparison of the two inversion models (modeling dataset, area B)
从表7可以看出Stumpf 2003模型的决定系数为0.706,Lyzenga 1985模型的为0.878,二者均方根误差相差不大。综上,Lyzenga 1985模型拟合度仍然优于Stumpf 2003模型。
图9所示为由区域B数据集得到的两种模型的回归标准化残差图。同样,两种模型与高斯曲线吻合,残差都基本符合正态分布。Stumpf 2003模型的标准偏差(1.427)显著高于Lyzenga 1985模型(0.963),后者的残差离散程度较小,分布更为集中。可以看到,根据Stumpf 2003模型预测的水深与真实值的误差集中于-2~1.5 m之间,而根据Lyzenga 1985模型预测的水深与真实值的误差集中于-1~1.5 m之间。
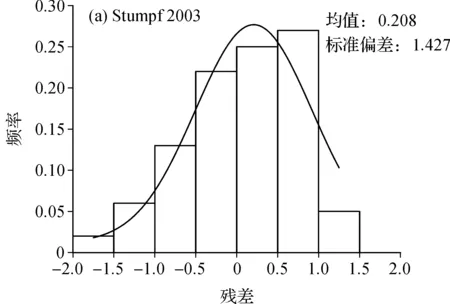
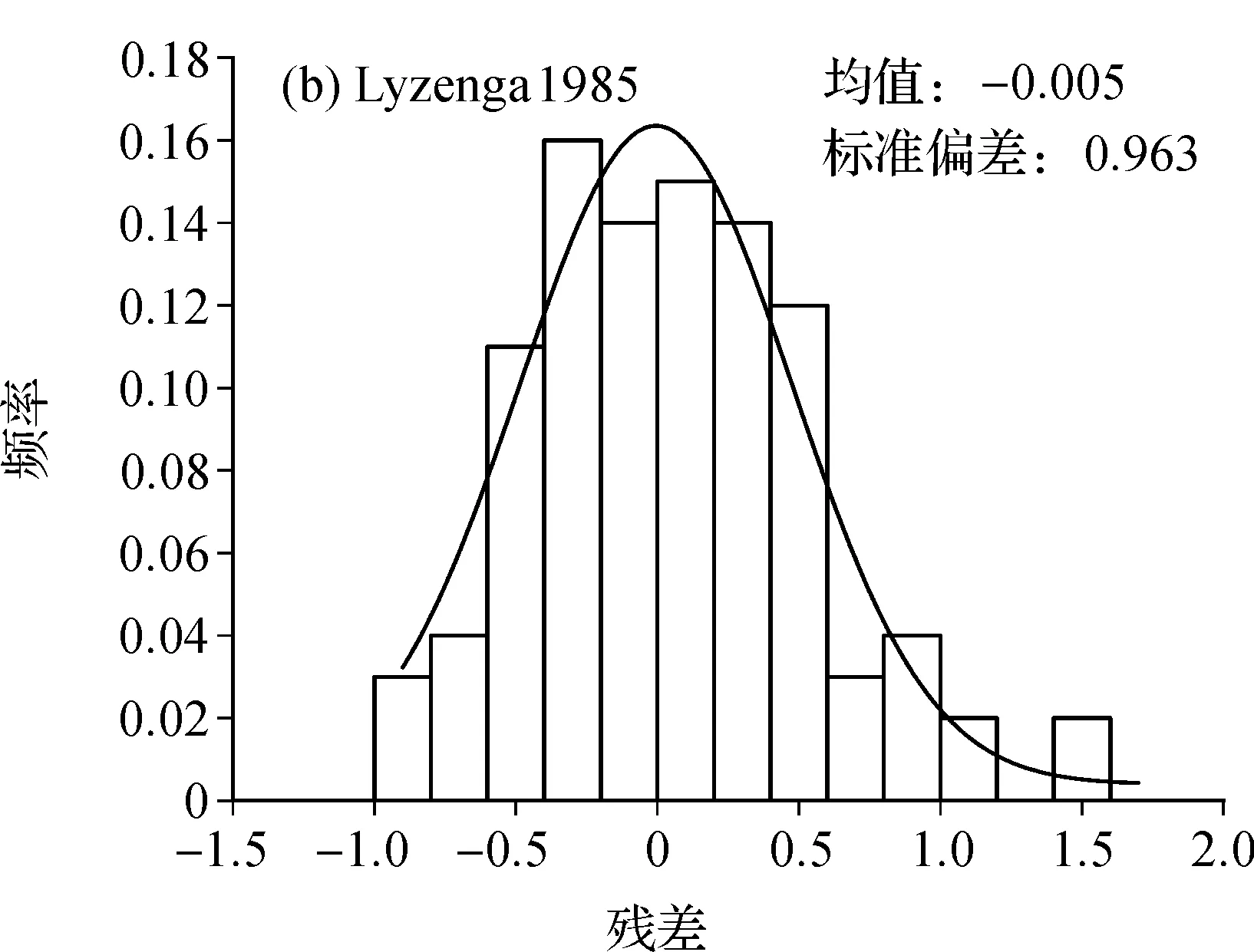
图9 两种模型的回归标准化残差图 (建模数据集,区域B)Fig.9 Regression standardized residuals of the two models(modeling dataset, area B)
4.3 验证
本节利用未参与建模的数据集对4.1与4.2节中建立的模型进行验证。
4.3.1 区域A的验证
利用未参与建模的110个样本的数据集对区域A模型的验证结果如图10和表8所示。

图10 反演水深与实测水深对比(验证数据集,区域A)Fig.10 Comparison of the retrieved depth and the in-situ depth(validation dataset, area A)

表8 两种反演模型的误差比较(验证数据集,区域A)Tab.8 Error comparison of the two inversion models (validation dataset, area A)
由验证结果可知,Lyzenga 1985模型水深反演的决定系数R2和均方根误差RMSE均优于Stumpf 2003模型。
4.3.2 区域B的验证
利用未参与建模的25个样本的数据集对区域B模型的验证结果如图11和表9所示。

图11 反演水深与实测水深对比(验证数据集,区域B)Fig.11 Comparison of the retrieved depth and the in-situ depth(validation dataset, area B)

表9 两种反演模型的误差比较(验证数据集,区域B)Tab.9 Error comparison of the two inversion models (validation dataset, area B)
由验证结果可知,Lyzenga 1985模型水深反演的决定系数R2较为显著地优于Stumpf 2003模型,均方根误差RMSE小于Stumpf 2003模型。
结合两种底质区域的验证结果可知,在水体清澈的不同底质区域,Lyzenga 1985模型普适性比Stumpf 2003模型更强,能够呈现出较为稳定的反演效果。
5 结论
本文利用高分辨率的WorldView-2影像反演了南海北岛附近浅海水深。采用了Lyzenga 1985和Stumpf 2003两种水深反演模型,并利用L-M算法求解模型参数。针对两种不同的底质进行了水深反演与对比分析,根据A区(珊瑚底质)和B区(砂质底质)的验证数据,得到结论如下:
(1)由决定系数R2可知:对于A区和B区,Lyzenga 1985模型的决定系数(0.902,0.897)均优于Stumpf 2003模型(0.882,0.779)。
(2)由均方根误差RMSE可知:对于A区和B区,Lyzenga 1985模型的均方根误差(1.651,0.529)均优于Stumpf 2003模型(6.421,0.723)。说明利用Lyzenga 1985模型反演的水深值与实测值之间偏差较小。
综上,在水体清澈的不同底质区域,Lyzenga 1985模型普适性比Stumpf 2003模型更强,能够呈现出较为稳定的反演效果。
