基于分解集成策略和多目标优化算法的混合预测模型在电力负荷预测中的应用
2021-01-27杨靖萍
吕 勤,杨靖萍,李 峰
(1.国网浙江省电力有限公司金华供电公司,浙江 金华 321000;2.北京众智新能科技有限公司,北京 100080)
电力负荷预测在电力系统安全中起着重要作用,已成为电力系统调度不可或缺的组成部分。提高预测的准确性和效率可以提高电力系统的安全性,经济性和可靠性,并促进电力企业合理的配电计划设计。
电力负荷预测可以减少由于电力供需不匹配而造成的潜在损失。电力需求被视为国民经济的晴雨表,准确的电力预测也可以帮助经济管理者掌握一个国家或地区的未来经济发展趋势。因此,准确预测电力负荷非常重要。
1 概述
一直以来,学者们对电力负荷预测进行了大量研究,取得了明显的成果。常见的预测方法主要包括支持向量机(SVM)[1]、整合移动平均自回归模型(ARIMA)、极限学习机(ELM)[2]和灰色模型[3]等,随着研究的深入,预测方法也逐渐被完善。黄伟等[4]运用指数平滑法将有起伏变化的原始数据序列变换成近于指数增长的新样本数据序列。然后采用灰色方法进行预测,提高了预测精度,取得了满意的结果。Li等[5]使用加权ELM方法用于处理不平衡类分布的数据,并根据Adaboost框架的训练样本的重要性确定适当的样本权重,但在处理复杂数据时预测不准确。Cao等[6]将ENN应用于非线性动力系统的辨识,均在一定程度上提高了电力负荷的预测准确性。马立新等[7]通过SOM特征提取找出与预测日同类型的历史数据作为训练样本,然后建立ELM模型,实验结果证实了预测模型得良好性能。表1中列出了常用电力负荷预测模型的实用性、优越性及局限性。

表1 常用电力负荷预测模型对比
在本文中,为了提高预测的准确性和稳定性,首先采取互补集合经验模态分解模型(Complementary ensemble empirical mode decomposition,CEEMD)对原始数据进行去噪处理,降低数据中的噪声污染,其次,以预测精度和稳定性同时作为目标的多目标蚁狮优化算法(Multi-objective ant lion optimization algorithm,MOALO)搜索Elman神经网络(Elman Neural Network,ENN)中的最优参数。本文提出的方法先进性如下。
a.互补集合经验模态分解模型克服了集合经验模态分解方法中模态混叠的现象,降低了原有数据中的噪声干扰,提高了神经网络建模的效率和性能。
b.相比于以往常用的单目标优化算法只考虑了预测精度,基于多目标蚁狮优化算法的Elman神经网络,兼顾了Elman神经网络的预测精度和预测稳定性,为实际电力负荷预测提供了兼具精度和稳定性的预测结果。
c.混合CEEMD-MOALO-ENN模型结合了数据预处理、参数优化以及预测模型3个模块,融合了3个模型在预测中的作用与优势,提高了电力负荷预测的准确性。
2 混合预测模型设计
2.1 互补集合经验模态分解模型
CEEMD被用于在电力负荷预测中的分解与集成。CEEMD方法是由Yeh等人开发的,用于改进EMD和EEMD的分解方法。EMD可以通过筛选过程将原始时间序列分解为几个本征模态函数(Intrinsic Mode Function,IMF),筛选过程需要多次迭代,直到符合特定的停止标准,然后生成有限数量的IMF。然而,EMD有一个严重的缺点:在筛选过程中容易产生模式混合问题。为了解决这个问题,Wu and Huang(2008)引入了EEMD,通过将白噪声添加到数据中,从根本上解决了模式混合问题。与EMD相比,EEMD有了很大的改进,并且可以显著提高稳定性,但是它不能完全抵消所增加的噪声。然后提出了CEEMD,它既可以保证EEMD的分解效果,又可以通过包含正信号和负信号的成对噪声来减少由添加的白噪声引起的重构误差[8]。考虑到与其他分解方法相比的优越性,本文将CEEMD用作分解方法。CEEMD的分解原理可以简述如下。
a.通过将N个成对的正高斯白噪声和负高斯白噪声添加到原始信号,2N个信号集表示为
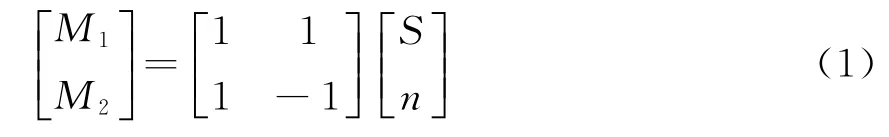
式中:S为原始信号;n为高斯白噪声;M1,M2分别为原始序列与正负白噪声的和。
b.对目标信号进行EMD分解,每个信号获得一组IMF分量,其中第i个成分的第j个IMF分量表示为imfij。
c.在对所有集成进行平均后,得到每个IMF的结果
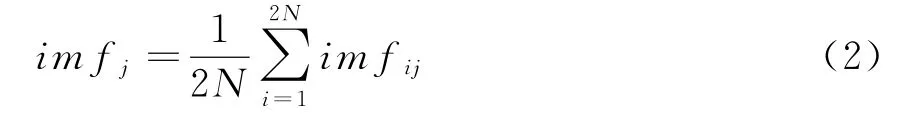
因此,CEEMD的最终分解结果x(t)可以表示为

在CEEMD中,集成数量和添加的白噪声的振幅分别设为200和0.2。
2.2 多目标蚁狮优化算法
多目标蚁狮优化算法(Ant lion optimization algorithm,ALO)是由Mirjalili等人在蚁狮算法的基础上提出的,因此,在介绍多目标优化算法之前,本文首先对蚁狮算法进行介绍。
2.2.1 蚁狮优化算法
受自然界中蚁狮狩猎机制的启发,Mirjalili等人首次提出了一种新颖的蚁狮优化算法。具体步骤如下[9]:
a.蚂蚁随机行走。蚂蚁在自然界中随机移动以寻找食物,它们的行为可以表示为

式中:cumsum为累加和;m为最大迭代次数;k为随机游走步长。为了在搜索空间内进行随机行走,采用最小-最大归一化,蚂蚁的位置可以通过式(5)获得

b.设置陷阱。为了获得更高的概率捕捉蚂蚁,识别出最优的蚁狮,选择蚁狮采用轮盘赌选择机制。
c.陷入蚁狮的陷阱中。利用式(6)和(7),对蚂蚁受蚁狮陷阱影响的随机行进行模拟:

式中:ck和dk分别为第k次迭代中的所有最小值和最大值的向量;和分别为第t只蚂蚁所有维度的最小值和最大值;为第t只蚁狮在第k次迭代中的位置。
d.将蚂蚁推向蚁狮。随着迭代,蚂蚁渐渐靠近陷阱中央。为了将蚂蚁推向蚁狮,需要缩小空间范围,有效提高收敛速度,在优质解范围内进行集中搜索,得到最优结果。
e.捕捉猎物并重建陷阱。蚁狮狩猎行为的最后1个阶段是捕捉1只到达坑底的蚂蚁,然后蚁狮再更新他们的位置等待并捕获新的猎物,算法如下
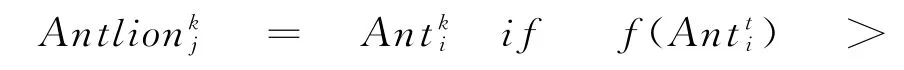

该算法将获得的最佳蚂蚁视为精英,在优化过程中被用来存储最优解,对整个蚂蚁的各个阶段都有一定的影响。受轮盘赌和精英同时影响,每只蚂蚁随机向选定的蚁狮移动,可以表示为

2.2.2 多目标蚁狮优化算法
对于多目标优化问题,多个目标之间常常是冲突的。实际上,多目标优化问题的解是一组称为Pareto最优解集的解,其中包括目标之间的最佳权衡,也称为Pareto最优解[10]。
与单目标优化算法不同,多目标优化算法需要同时考虑多个目标函数。基于此,引入了Pareto最优来解决这个问题,主要包括Pareto占优、Pareto最优解、Pareto最优解集合Pareto前沿面5个概念。
因此,Pareto最优解即多目标蚁狮算法需要求的解。为了寻找具有高多样性的Pareto最优解集,该算法采用领导选择和档案维护来存储Pareto最优解,并利用轮盘赌和式(9)从档案中选择非劣解。
此外,为了改善档案中解的分布,多目标蚁狮使用了2种机制。
第1种:蚁狮是从种群最少的解中选择的,被蚁狮选择的概率为

式中:Nj为第j个解附近的解的个数;c为固定常数。
第2种:如档案已填满,则会删除集中的解,以容纳新的解,移除概率为1/Pj。
最终,为了解决多目标问题,蚁狮优化算法中的式(8)应该修改为

2.2.3 Elman神经网络
Elman神经网络由J.L.Elman在1990年提出的。它可以看作是具有局部存储单元和局部反馈连接的递归神经网络,分为输入层、隐藏层、承载层和输出层。网络的承载层可以传输状态信息并具有存储能力,可以帮助ENN获得更好的预测。特别是在解决时间序列数据问题时,ENN是理想的选择[11]。
ENN的非线性状态空间表达式为
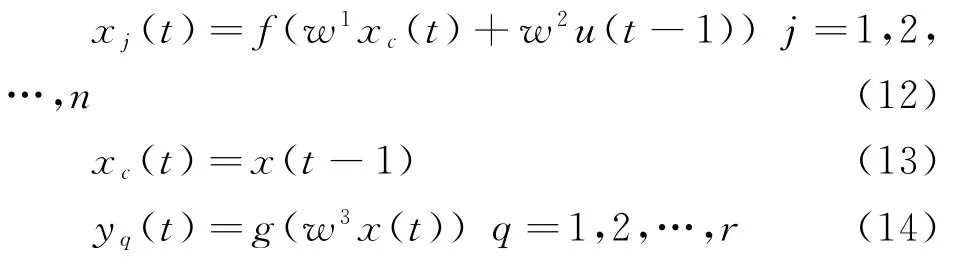
式中:w1为承载层和隐藏层之间的权重矩阵;w2为输入层和隐藏层之间的权重矩阵;w3为隐藏层和输出层之间的权重矩阵。g( ·)代表输出层中的激活函数,而f(·)代表隐藏层中的激活函数。
3 实证分析
3.1 实验数据
为了验证提出的混合预测模型在电力负荷预测中的良好性能,选取了浙江省2011-2018年社会月度用电量的数据进行实证研究。如图1所示,其中,2011-2016年共72个数据作为训练集建立模型,2017-2018年共24个数据作为验证集,检验模型的预测性能。

图1 浙江省2011—2018年社会月度用电量数据
3.2 评估指标
为了量化评估不同预测模型的预测性能,选取了一系列的评估指标对不同模型的预测结果进行对比。本文选取平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)来评价预测精度。与平均误差相比,MAE能够更好地反映预测误差,因为偏差的绝对值是用来计算和避免正负值的抵消效应的。RMSE对超大、超小值比较敏感,能更好地测量值的精度。MAPE消除了量纲的影响,可以更客观的对比不同模型之间的预测精度。此外,采用预测的一致性指数(IA)用于测量观测值和预测值的相似度,采用方向精度(DA)来计算预测方向的正确性。
3.3 结果分析
为了验证本文提出的混合预测模型的优越性,本章对比了CEEMD-MOALO-ENN、MOALO-ENN、ENN以及3个传统的流行的预测模型:反向传播神经网络(BPNN)、极限学习机(Extreme Learning Machine,ELM)和ARIMA。如表2所示,CEEMD-MOALO-ENN在所有模型中预测精度最高,在所有评估指标表现最好。

表2 不同模型预测结果对比表
对比CEEMD-MOALO-ENN和MOALOENN,可见分解集成策略可以有效提高预测预测精度,以MAPE为例,CEEMD-MOALO-ENN的值为8.320 4%,MOALO-ENN的值为10.610 6%。对比MOALO-ENN和ENN,ENN的MAPE为12.581 2%,可以证明优化算法在混合预测模型中的有效性。对比CEEMD-MOALO-ENN和其他3种传统的预测方法,在3种传统预测方法中,ARIMA的预测效果最好,BPNN的预测效果最差,3种预测模型的效果均比本章提出的CEEMD-MOALO-ENN混合预测模型效果差。
4 结论
考虑到电力负荷预测在电力系统中的重要作用,本文提出了基于分解集成策略和多目标优化算法的混合预测系统,对浙江省社会月度用电量进行预测。具体而言,在预测之前,首先对数据进行预处理,采用分解集成策略分解出原始序列中的噪声序列,然后将剩余序列集成,大大减少了原始数据中的噪声污染,提高了预测模型的稳定性。其次,采用多目标优化算法,平衡预测精度和稳定性,提高Elman神经网络的预测性能。通过将本文提出的混合预测模型与其他对比模型的比较发现,提出的混合预测模型在电力负荷预测中具有一定的优越性,数据预处理技术和优化算法均能在一定程度上提高预测模型的性能,为电力负荷预测提供了新的思路。
