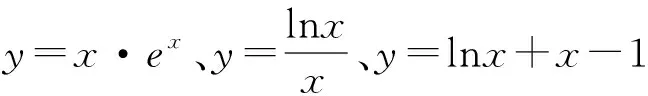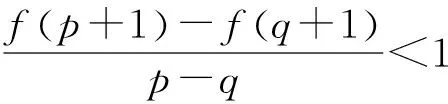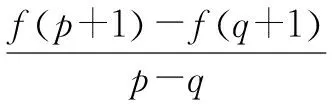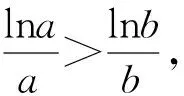不等式问题中的同构变形策略

山东省宁阳复圣中学 (271400) 张志刚

同构，在抽象代数中指一个保持结构的双射,在高中阶段则表示结构或形式相同.在很多不等式问题中，经过同构变形使不等式两侧呈现相同结构，然后构造函数，结合复合函数的单调性，将不等式蕴含的特征与属性清晰明朗地呈现出来，可解决求参数的取值范围、零点的个数、证明不等式等问题，此种解法不妨称为同构法.例如,若F(x)≤0能等价变形为f[g(x)]≤f[h(x)]，然后利用外层函数f(x)的单调性，转化为g(x)≤h(x)或g(x)≥h(x).例如：

(2020年全国Ⅰ卷理科第12题)若2a+log2a=4b+2log4b，则( ).

A.a>2bB.a<2bC.a>b2D.a

分析：由于2a+log2a=4b+2log4b=22b+log2b<22b+log2(2b)，设f(x)=2x+log2x,则f(a)

策略一：借助移项、四则运算等同构变形

对于较为简单的多项式函数，可根据题设条件，通过移项、四则运算等变形，直至不等式两侧呈现相同的结构，之后引进新函数，利用函数的单调性解决问题.

例1 (2020年全国Ⅱ卷理科第11题)若2x-2y<3-x-3-y，则( ).

A.ln(y-x+1)>0 B.ln(y-x+1)<0

C.ln|x-y|>0 D.ln|x-y|<0

解：由题意得2x-3-x<2y-3-y.设f(x)=2x-3-x，则f(x)1，ln(y-x+1)>0.选A.

点评：例2中通过对已知不等式变形，使不等式两边结构相同，适时引入函数g(x)，进而将问题转化为不等式g′(x)≥0恒成立问题，通过分离参数可轻松获解.

策略二：借助取对数运算同构变形

数据处理中，我们经常对原始数据取对数，然后再作出处理.依据主要有二，一是通过取对数可以大幅压缩数据的绝对数值,数据更趋平稳.本质上是：当x的取值很大时，对数函数变化速度非常缓慢；二是通过取对数降低运算的维度.由于logaMn=nlogaM，loga(M·N)=logaM+logaN，a>0，a≠1，M>0,N>0取对数后，乘方运算转化成了乘法计算，乘法运算则转化成了加法计算.对于两边均是指数型不等式，可考虑通过取对数，将指数问题转化为对数问题，降低思维难度.

例3 已经b>a>e，求证：ab>ba.

策略三 借助恒等式b=alogab代换同构变形

由对数的概念易知等式alogab=b(a>0，a≠1，b>0)成立，我们常常利用该式简化计算.但逆向观察该式，则有b=alogab，特殊的a=elna，可以发现幂函数式可等价变形为指数式，必要时实施此代换，可将一些结构不良的不等式变形为不等式两边相同的结构特征，然后引入新函数求解.

例4 (2020年新高考全国I卷第21题)已知函数f(x)=aex-1-lnx+lna.(1) 当a=e时,求曲线y=f(x)在点(1，f(1))处的切线与两坐标轴围成的三角形的面积；(2) 若f(x)≥1，求a的取值范围.

点评：本题的难点是将不等式aex-1-lnx+lna≥1进行变形，利用恒等式a=elna和x=elnx代换，实现幂函数、指数函数、对数函数式之间的相互转化,使不等式变形为更协调的elna+x-1+lna+x-1≥elnx+lnx形式，然后构造函数g(x)，利用g(x)的单调性，将问题简化为lna+x-1≥lnx恒成立问题.

例5 设k>0，若存在x>0，使得不等式log2x-k2kx≥0成立，求k的取值范围.

点评：利用恒等式x=2log2x，将(log2x)·x≥kx·2kx变形为(log2x)·2log2x≥kx·2kx，此时不等式两边的结构一致，然后引入函数f(x)=x·2x，利用f(x)在(0，+∞)上单调递增得log2x≥kx，通过分离参数转化为函数g(x)的最值问题.

然而，同构变形技巧性强，需要学生具备较全面的知识储备、较高的关键能力和素养，而这些显然不是一朝一夕就能轻松练就的.教师要通过典型题目的剖析讲评，结合题设条件将被破坏的结构进行还原变形，直至不等式同构形式，然后选择构造新函数，结合函数的单调性等性质简化不等式，即将原不等式中蕴含的内在规律外显化，揭示问题的丰富背景和内涵，让学生在惊讶于同构法巨大威力的同时，又不会感到其玄妙莫测和出其不意.通过对解题过程的思维分析，留住知识之“根”，方法之“根”，价值之“根”和本质之“根”.