基于Lasso-Logistic模型的个人信用风险评估
——来自微贷网的数据分析
2021-01-27李淑锦嵇晓佳
李淑锦,嵇晓佳
(杭州电子科技大学 经济学院,浙江 杭州 310018)
随着我国居民生活水平的提高以及金融体制改革的加快,人们的消费观发生了很大的转变,提前消费(信贷消费)开始进入人们的生活。据中国支付清算协会的数据,个人消费信贷规模不断扩大,2020年第二季度,我国人均银行卡持有量达到6.18张,其中,信用卡人均持有量0.54张。个人消费信贷在提高消费者幸福指数和改善金融机构资产结构的同时,信用风险也逐步凸显。基于此背景,排除高风险借款人群,降低个人消费信贷违约风险,成为消费信贷领域亟待解决的问题。
已经有国内外学者对个人借款者的信用风险评估进行探讨。关于信用风险评估模型的研究,Ohlson(1980)[1]首次利用Logistic回归构建了有关信用分类模型,并且得到明显的分类效果;Sustersic等(2009)[2]在缺乏一般评估方法所需要的信用评估数据时使用人工神经网络模型对个人借款者的信用风险进行评估;黄震(2015)[3]通过BP神经网络模型导入个人借款者的相关信息来分析其违约情况;师应来等(2018)[4]得到非线性模型的预测精度更高的结论;还有学者对信用风险的评估指标进行了相关研究。Stein(2002)[5]将信用风险度量指标分为硬信息(一些客观存在的信息)和软信息(一些描述性信息)两类。李思瑶等(2016)[6]在Stein的风险度量指标体系下进行实证分析,研究发现借款人的收入、所处区域、学历水平及信用评级和违约率负相关。Barasinska和Schäfer(2014)[7]发现性别也是影响借贷成功的因素;廖理等(2014)[8]研究发现借款者的地域分布与其借款成功相关。
在资本市场上,资本具有逐利性,当资本出借人在决定投资某个项目时,很可能会模仿他人的选择,从而导致羊群效应。关于羊群效应,Bikhchandani和Sharma(2000)[9]定义了股票市场的羊群效应并对其成因加以阐述。伍旭川和何鹏(2005)[10]探究了中国开放式基金市场上的羊群行为,发现存在较强的羊群效应且会对股票市场产生影响。廖理等(2015)[11]使用P2P数据证实了羊群效应的存在,且当借款信息不对称程度越高,羊群效应越强,持续时间越短。张科和裴平(2016)[12]具体分析客观存在信息和描述性信息对羊群效应产生的影响;关于羊群效应与信用风险关系的研究,Herzenstein等(2011)[13]经实证得到羊群效应有利于维护借贷双方利益的结论。Lee和Lee(2012)[14]提取了韩国网贷平台的借款者数据,得出羊群效应(群体智慧较大)可以降低投资者风险。Mollick和Nanda(2015)[15]根据美国Kickstarter平台的数据得出群体智慧可以预测专家意见。Baruch等(2014)[16]的研究表明,如果存在部分具有独立观点的市场参与者时,群体甚至能够修正专家发布的错误信息。
综上所述,国内外学者关于信用风险评估方法以及股票市场中的羊群效应研究成果丰富,关于个人借贷的羊群效应的研究则主要集中在羊群效应是否存在的问题,尚未出现将羊群效应纳入信用风险评估模型的研究,因此建立一个体现群体智慧因素背景下能有效评估个人借款者信用风险的模型来预测个人借款者的违约风险是非常必要的和迫切的。本文将羊群效应作为个人信用风险的一个评估指标,并且将Lasso和Logistic模型结合优势互补创建Lasso-Logistic模型,首先用Lasso模型对评估指标进行筛选,剔除冗余变量,再利用Logistic模型对个人借款者的信用风险进行评估,是本文的主要研究内容和创新点。
一、信用风险评估方法
国内外学者关于个人信用风险评估方法有两大类:统计型和非统计型。统计类的评估模型一般有:Logistic回归、贝叶斯和决策树等;非统计方法包括SVM模型和神经网络模型等。常见各种方法的优缺点见表1。

表1 各类评估方法的比较
从表1可以看出,每个方法各有自己的优缺点,如Logistic模型解释性高,建模简单,但容易导致欠拟合;Lasso模型预测精度高,能解决多重共线性和拟合问题,但是计算过程相对复杂等。这些模型的共性是都不能完全对模型的变量进行有效解释。近年来不少学者将具有互补特点的模型进行组合来创建新的信用评估模型。向晖(2011)[17]将单一模型和组合模型进行对比,发现组合模型会有更高的预测精度,且模型的可解释性和稳健性都有所提高。
本文将Lasso和Logistic模型结合起来构建新的评估方法,原因如下:(1)Lasso和Logistic模型具有一定互补性。Logistic易造成欠拟合问题,而Lasso正好能解决多重共线性和拟合问题;Lasso计算过程复杂,但是Logistic模型较简单且实现难度低;(2)两个模型都可以解决非线性问题,且二者对数据的假设条件都较低。将Lasso和Logistic模型相结合构建新的评估方法-Lasso-Logistic模型,从理论上看能够提高模型预测的准确率以及可解释性。
(一)Logistic回归
Logistic回归模型的基本原理如下:设yi表示第i个借款者是否违约,自变量xi1,xi2,…,xim则代表影响借款人i信用的m个信用相关指标,则有:
yi=f(xi1,xi2,…,xim)+εi,i=1,2,…,n
(1)
其中yi是二元离散变量,取值是0或者1。yi=0表示第i个借款者未违约,yi=1表示违约。已知第i个借款者信息x的前提下,定义其违约概率为p=P(yi=1|x),那么未违约概率为P(yi=0|x)=1-p。
Logistic回归方程表示为:
(2)
且当(1)式中yi为多元线性函数时,可以将yi表示为yi=∑βjxij,根据泰勒公式,Logistic回归模型可以表示为:
π*=β0+β1xi1+β2xi2+…+βmxim+εi=∑jβjxij+εi
(3)
(二)Lasso-Logistic模型
Lasso-Logistic回归模型是在普通Logistic回归模型的基础上,加入对参数的惩罚项来进行变量选择和参数估计。在本文的研究背景下,个人借款者是否违约是一个二元因变量,可以用0、1来表示。由于存在多个评估指标,需要剔除冗余变量,Lasso模型的特点符合本文的要求,因此本文构建Lasso-Logistic模型。
Lasso-Logistic回归模型中的参数估计可以表示为:
(4)
Lasso-Logistic回归模型中调和参数λ会直接影响到变量的选择结果。常用于选择调和参数的方法主要包括Boostrap、交叉验证、广义交叉验证,本文采用十折交叉验证方法来确定调和参数λ。
交叉验证法首先把数据分成数量大致相等的K份,用其中k-1份数据拟合模型fk,用获得的模型fk预测第k份数据得到预测误差。实践中,令k=1,2,…,K,重复上述过程,最后汇总K个模型的预测误差。如果K=10,就是十折交叉验证。
十折交叉验证的预测误差可以表示为:
(5)
其中k(i)是表示N个样本中观测i属于第k(k=1,2,…,K)份数据的指示函数,fk表示使用剔除第k份数据后拟合的模型。
假定拟合了一组含有调和参数的模型表示为fk(x,λ),定义:
(6)
那么CV(f,λ)就是一条随λ变化而变化的检验误差曲线,找到使其最小的λ,就得到Lasso-Logistic回归模型的调和参数:
(7)
在此基础上对应选取模型压缩后保留下来的自变量,得到Lasso模型确定的Logistic回归方程为:
(8)
此时模型只包含Lasso筛选后的变量。
二、个人信用风险评估指标体系及其赋值
廖理和张伟强(2017)[18]针对互联网借款平台中个人借款者的信息价值进行实证研究,结果表明个人借款者的所有信息都存在或多或少的价值,因此,本文选取影响个人借款者信用风险的相关变量建立个人信用风险评估的指标体系,包括个人借款者的特征、标的资产的特征和个人借款者的信用特征。结合实证分析时使用数据的可获得性,本文选取个人借款者的特征包括性别、年龄和婚姻状况;标的资产的特征包括借款利率、借款金额和借款期限;个人借款者的信用特征包括历史还清率、历史还清期数、待还清率、待还期数和历史逾期数等。根据学者们的研究,羊群效应也是影响借款者信用风险的一个指标。羊群效应一方面体现着群体智慧,另一方面,盲目跟从也会增加投资者的风险。
借鉴学者们的研究,将与违约率正相关的指标赋较大值,而和违约率呈负相关的指标赋较小值,具体各指标变量的赋值见表2。历史还清期数和待还期数若仅考虑次数显然不合理,将根据其在借款总次数中的占比进行赋值。历史逾期数则不同,逾期次数要比比率更能说明诚信度,因此便用逾期次数赋值。对于线性模型,数据归一化后,最优解的寻优过程明显会变得平缓,更容易收敛到最优解,因此本文将年龄、借款利率、借款金额和借款期限进行标准化处理。

表2 信用风险及评估指标赋值
三、数据来源与评估结果
(一)数据来源
由于个人借款者的数据难以获取,本文选择微贷网平台上个人借款者的相关数据来进行实证分析。在该平台上,筹资者需要提交相关的个人信息以及相应的借款数额等信息;投资者可以对各个项目进行筛选评估,选择相对更有利的项目。每一笔借款的投资金额以及投资时间可以从该平台上获取。微贷网平台则会对筹资者所提供的信息进行审核,并且根据这些信息对筹资者进行信用评级。
本文利用Python爬虫抓取了21 176个借款者的数据,其中存在924笔逾期数据。因为逾期数据远小于未逾期数据,数据间存在的极大不平衡性会影响样本预测的准确性。Weiss和Provost(2003)[19]通过实证检验发现,数据并不一定需要自然分布,为提高预测的精度,本文采用“减少多数法”对样本数据进行平衡处理,最终确定的有效样本个数是1 850个,其中包括924个逾期样本,926个正常样本。因为本文采用十折交叉验证(即将数据集分成10份,其中9份作为训练数据,1份作为测试数据进行检验),因此测试集数据为185个,其余数据均作为9份训练数据来进行训练;其中训练集中,违约样本832个,正常样本833个;测试集中违约样本92个,正常样本93个。
(二)羊群效应的度量
通常意义上,羊群效应是指市场上那些没有获得全部信息或者没有成熟投资经验的投资者模仿其他投资者的现象。本文将羊群效应进一步定义为投资者的羊群效应体现着群体智慧,是理性的。不同的学者根据研究目的不同,采取不同的方法对羊群行为进行测度。目前对个人借款平台羊群行为的测度方法主要有三种。第一种方法是根据投资人投标的份额大小来衡量羊群效应。如果随着时间的增加,一项投资标的的投资份额在增加,就说明该项目的投资存在羊群行为,且投标的份额随时间越来越大,那么羊群效应就越大;第二种方法是根据项目的投标速度来测度。如果当前投标次数增多而投资者所需要的平均投标时间却呈现减少状态,那么从侧面体现了存在羊群效应;第三种方法是根据后续投标来测度羊群行为。某项目当前获得的投标次数越多,那么从一定程度上显示着其他投资者对该项目的信任,从而,后续投资者会将该因素作为是否投标的因素。
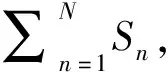
(9)
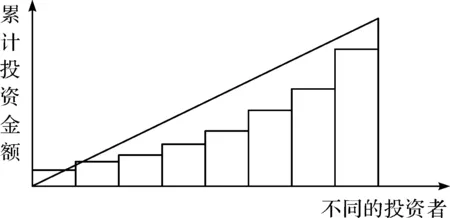
图1 羊群效应较大
Herding的取值范围为0到2,Herding值越大,表示羊群效应越小。Herding在0到1之间表示羊群效应较强,在1到2之间则表示羊群效应较小。本文通过t检验发现违约借款的羊群效应值显著低于未违约借款,即投资者对于违约借款会呈现出更弱的羊群效应,这意味着羊群效应具有一定的信息量,符合预期。
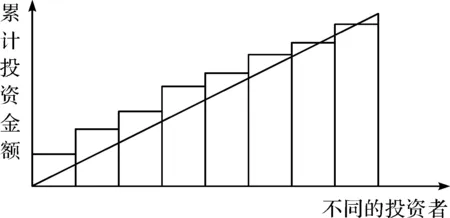
图2 羊群效应较小
(三)实证分析
由于12个信用风险评估指标对个人信用风险的影响不同,本文首先运用Lasso模型对评估指标进行筛选。通过相关软件进行十折交叉验证,得到图3。图3上面部分的横坐标表示模型经Lasso筛选得出的变量个数,下方的横坐标表示λ的取值范围(-8,-1),纵坐标表示模型在不同的λ取值时模型的均方差。根据学者Tibshirani(1996)[20]研究,λ估计值在图中两虚线之间时模型预测偏差波动幅度相对较小,建议选取使模型容易处理的λ值。
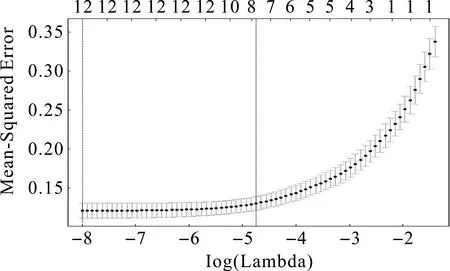
图3 Lambda与变量数目对应走势
图4显示了Lasso模型在不同λ值时所选择变量的系数表现情况:λ为-8时,对应自变量个数为12;λ为-2时对应自变量个数为1,即当λ取值变大时,惩罚项所筛选出的自变量个数减少。图4显示,λ取值在-4和-8之间时,筛选出来8个变量,删除的冗余变量是借款利率、年龄、历史还清率和待还清率。此时,基于Lasso-Logistic模型得到的参数估计结果如表3所示。

图4 Lasso系数解路径

表3 模型参数估计结果
因此,拟合的公式为:
Y=-0.856 7+0.105 2*H-2.1002*X11+0.552 1*X10+0.0310*X1+
0.011 2*X3-0.005 5*X5-0.059 5*X7+0.4077*X8
(10)
从公式(10)可以看出,羊群效应和违约正相关,因为羊群效应越大(赋值越小),群体智慧越大,违约发生的机会越小,符合本文的预期;借款期限与违约风险负相关,这是因为平台对长期的借款审核更加严格,对借款者的信用等级要求更高,违约风险相对降低了;借款总额、性别与违约风险正相关,符合预期;婚姻状况与违约概率成正相关,这说明未婚人群违约情况多于已婚人群,符合预期;历史还清期数与违约负相关,这也在一定程度上证明了本文对还清率定义的正确性,因为历史还清期数多并不等同于历史逾期数少;待还期数与违约负相关,这与历史还清期数相同,仅考虑次数显然不合理,待还期数多,不是意味着违约风险高,更大可能是该借款者刚进行借款活动,而支付期还没到或者所需支付的次数不多;历史逾期数与违约概率成正相关,从历史的违约次数可以在很大程度上得出借款者的违约风险,符合本文预期。
陈中飞等(2019)[21]的研究表明,中国互联网个人借贷平台对借款利率的定价存在问题,因此Lasso模型对其进行剔除是合理的;年龄作为冗余变量被剔除的原因是样本中借款者的年龄都集中在30-40岁,没有较大的区别;历史还清率和待还清率被剔除是由于本文的数据中多数借款者都是初次借款,因此不需要根据历史的借款次数及月份对此次借款者的借款状态进行分类讨论,Lasso模型对指标的筛选也是合理的。
(四)预测能力分析
本文分别测试了在评估指标一致的情况下,Logistic回归模型和Lasso-Logistic模型对违约的预测准确率,结果见表4。

表4 Logistic和Lasso-Logistic模型预测精度对比
从表4可以看出,使用Logistic模型,训练集的整体预测准确率为87.87%,测试集准确率为84.86%;而使用Lasso-Logistic模型,训练集准确率达99.04%,测试集准确率达96.76%,准确率都大大超过了Logistic模型。在个人信用风险的实际评估中,如果实际借款者违约,但是预测结果是借款者未违约,也就是说有违约风险的不良借款人被识别为没有违约风险的优良借款人,它所带来的损害远大于将优良的借款者识别为不良借款者。因此当模型将不良贷款者看成优质贷款者的概率越小,这个模型才具备对更优质借款人的识别能力。对于测试集,Lasso-Logistic模型犯这类错误的概率是4.35%,远小于Logistic模型的27.17%,因此Lasso-Logistic模型的评估结果优于Logistic模型。
表5是在其他因素不变的条件下,利用新建的Lasso-Logistic模型,通过添加或删除羊群效应这一指标来判断群体智慧是否是个人借款者信用风险的主要影响因素,即能否提高预测的精确度。从表5可以看出剔除了羊群效应指标后,Lasso-Logistic模型的预测精度仅有84.32%,与Logistic模型的预测结果类似,与添加羊群效应指标后的预测精度96.76%相比,预测精度大大降低,再一次证实了羊群效应,即群体智慧对违约风险的影响是不容忽视的。

表5 羊群效应对预测结果的影响
综上所述,Lasso-Logistic模型在个人借款者的信用风险评估中,评估结果令人满意,并且该模型得出的各评估指标的经济意义,与文中理论分析的结果一致,进一步证明了本文选取的评估指标是合理的。微贷网上的借款者信息中,性别、婚姻状况、借款金额、借款期限、历史还清期数、待还期数、历史逾期数、羊群效应这8个指标成为了个人借款者信用风险重要的影响因素,同时Lasso-Logistic模型的结果为预测借款者信用风险提供了参考,减小了投资者的投资风险。
四、结论
本文立足于个人借款者,通过理论分析个人借款者信用风险的影响因素,选取了包括羊群效应、借款人的特征、借款人的信用特征以及标的资产特征等指标建立个人借款者的信用风险评估指标体系;借鉴Lasso模型和Logistic回归方法的优势,构建Lasso-Logistic信用风险评估模型;然后利用微贷网平台借款者的数据进行实证分析,结果表明,Lasso-Logistic模型在预测借款人的违约概率时确实优于一般的Logistic回归模型。本文的主要结论是:
1.Lasso模型可以筛选出个人借款者信用风险评估的有效指标
个人借款者信用风险评估的指标较多,但有些指标是无效的、冗余的,只能增加评估的难度并不能改善评估的结果。本文利用Lasso对指标进行筛选,将初选的12个指标的评估体系降低为8个指标的评估体系,使得Lasso-Logistic模型的计算更加快捷。
2.Lasso-Logistic模型的预测精度高于Logistic回归模型
无论对训练集还是测试集,不管是对违约客户的预测还是正常客户的预测,Lasso-Logistic的准确率都高于Logistic回归模型。利用Logistic模型进行评估,训练集的整体预测正确率为87.87%,测试集的预测精度84.86%;而利用本文构建的Lasso-Logistic模型,训练集准确率高达99.04%,测试集准确率也高达96.76%,准确率都大大超过了Logistic模型所预测的精度。进一步说明该模型在个人信用风险评估中的适用性。
3.羊群效应是影响个人借款者信用风险的重要指标
在建立个人借款者的信用风险评估指标体系时,本文创新性地引入了一个新的变量——羊群效应,根本原因在于:大数据时代,每个人都能够通过自己的努力去寻找一些重要信息来控制投资风险,因此多数人就能得到不同的、有价值的信息,使得总体信息更接近完全信息,这对于违约风险的预测是十分重要的。实证结果表明,在其它评估指标不变的条件下,利用Lasso-Logistic模型对测试集进行预测,含有羊群效应的模型预测借款者是否违约的整体预测精度高达96.76%,远高于不考虑羊群效应的准确率84.32%。
