多元回归方法在芹山水库流域年降雨量系列插补的应用

2021-01-27陈信花吕泽浩潘志浩

中国农村水利水电 2021年1期

陈信花，吕泽浩，潘志浩

(1.华电宁德电力开发有限公司，福建宁德 352100；2.太原理工大学水利科学与工程学院，太原 030024；3.武汉大学水利水电学院，武汉 430072)

0 引言

穆阳溪流域属交溪水系，是福建省五大河流之一交溪的一级支流，位于福建省东北部，穆阳溪流域面积1 389 km2，主河道长132 km，河道平均坡降7.49‰，天然落差为820 m，芹山水库位于福建省周宁县，于1999年底建成并蓄水，至今已安全运行21年，为保证今后安全运行, 有必要对水库的流量指标进行复核。但是流域内雨量站资料不够完整，无法进行产汇流计算，得到流量等一系列水文要素。针对这一问题，目前插补缺失的降雨数据的方法有相似性插补法，空间插补法，气象要素混合插补法,地形影响因子插补法等[1]，这些方法对其他相关资料的要求更高，而一些区域由于气象站运行方式为无人值守数据采集以及传输受到电力通信条件的限制，相关资料更加难以获取[2]。而在水文问题中数值相关通常按照数理统计中的回归相关进行特别是当相关点群相当散漫时，利用回归分析模型，只需将建库前的完整降雨资料加入已知的降雨资料系列中, 计算建立回归方程，便可获得其缺测漏测年份的降雨资料，进一步用于水库流量校核[3]。其中求解回归模型的参数仍比较难求解，本文采用最小二乘法，通过不同站点的均方误差比较，采用最优的回归模型进行水文资料的插补和，从而使插补结果更精确。因此，此方法对穆阳溪流域各站水文资料进行插补，为流域内水利规划、水资源调查评价、水资源合理配置等工作提供基础依据，具有非常重要的现实意义[4]。

1 流域及水库概况

芹山、周宁水电站位于福建省穆阳溪流域，位于福建省东北部，发源于福建省鹫峰山脉北端东南侧政和县的镇前和澄源之间的南山岗。流经周宁县泗桥、纯池、浦源，吸纳周宁城关和七步等地来水后在文潭村流入福安市穆阳和康厝诸地，在赛歧镇上游约2 km处汇入交溪。芹山、周宁水电站的径流资料包括芹山坝址及附近流域内所有雨量站60 a年降雨量资料(1958-2017年)和七步站60 a(1959-2017年)逐月降雨径流资料。芹山坝址上游流域内共有纯池、澄源、镇前、前溪和泗桥等5个雨量站，其中纯池雨量站资料完整，澄源、镇前和泗桥3个雨量站资料在1958-1991年、2007-2017年间资料完整，1992-2006年间降雨量资料有不同程度的缺失，其中七步、际头雨量站资料完整，由于雨量站降雨量资料不齐全，需对雨量站的降雨系列进行插补。

2 年降雨量插补方法

2.1 回归分析

雨量站在地区中的时空分布不连续，需要将相邻、相似流域或地区的站点，且具有相同系列的参证站资料通过回归分析后，将具有长系列的参证站点资料插补至缺测雨量站中。所以当流域中缺少长期测站时，可利用自然地理条件相似的邻近流域的雨量站作为参证站，通过对已有完整的水文数据与缺测站点的部分水文数据建立进行回归分析，便可以达到展延水文资料的目的。

降雨资料插补时，参证变量和设计变量应遵循如下原则：①有密切的成因关系;②具有同步系列的参证站资料[5];③参证站需有足够长的时间系列资料。

具体数学方法如下：多元线性回归方程的形式为:

y=β0+β1x1+β2x2+…+βkxk+ε

(1)

如果我们获得n组观测数据,其中每一组观测

yi=β0+β1x1i+β2x2i+…+βkxki+εi

(2)

式中:i=1，2，…,n;则上式可写为矩阵形式Y=XB+ε，即:

(3)

由最小二乘法求得回归系数β0,β1,…,βk，使得：

Qe=Q(β0,β1,…,βk)=

(4)

(5)

从而使因变量的观察值与估计值之间的离差平方和达到最小来求得回归系数，求解各回归参数的标准方程如下,分别求Qe关于β0,β1,…,βk的偏导数，并令其为0。

(6)

利用SPSS或Excel分别对已知长系列降雨资料分别与需要插补降雨资料的雨量站进行一元、二元、三元回归分析求出相应回归方程，但是要注意在某些实际问题中，模型回归系数不能任意取值，可能有一定的约束，应用到具体情况中应注意[6]。

2.2 显著性检验

显著性检验就是事先对总体(随机变量)的参数做出一个假设，然后利用样本信息来判断这个假设是否合理。R检验是对每一个回归方程相关程度的好坏进行检验，R表示所有自变量与因变量的相关程度，其值越接近于1，表示相关程度越高，回归关系越显著。

(7)

F检验中要检验自变量是否与因变量呈线性相关，即检验原假设是H0否成立。其中备择假设为H:β1=β2=…,βk=0。当H0成立时，线性相关，否则相关性不显著。统计学中应用统计量F检验H0。

(8)

式中：F服从自由度(m，n-m-1)为的F分布，即F～F(m，n-m-1)。给定置信度α，若P[F≤Fα(m,n-m-1)]=1-α成立，则假设H0成立，否则，拒绝原假设，接受备择假设即线性认为相关。

均方误差是反映估计量与被估计量之间差异程度的一种度量。常常作为一种衡量回归程度好坏的指标。其公式为：

(9)

3 实例应用

为了保证插补准确度，选取合理的降水资料插补处理尤为重要[7]。在所有降雨资料中，纯池站、七步站与际头站为资料完整的雨量参证站。以澄源、泗桥、镇前雨量站为待插补雨量站，分别与纯池、七步、际头雨量站建立一元回归方程，与纯池和七步，七步和际头，际头和纯池雨量站建立二元回归方程，与纯池站、七步站、际头站建立三元回归方程。经过R检验与F检验，上述所有回归方程均通过置信度α=0.05的显著性检验，自变量与因变量有一定的相关关系。为了选择最优的回归模型，计算所有回归方程的均方误差，取回归方程中均方误最小的拟合方程作为其实际的回归方程。选取最近五年作为检验期，其余年份作为率定期(如表1所示)以纯池、七步、际头雨量站为参证站，澄源、泗桥、镇前雨量站为待插补雨量站，分别应用以上方法推求一元、二元及三元回归关系，并以均方误差最小作为评判回归关系优劣的依据，且以相对误差小于等于20%作为合格标准、计算其率定期合格率，如表2所示。将各待插补站的最优回归方程应用于检验期各年份降雨量计算，其计算成果如表3所示。

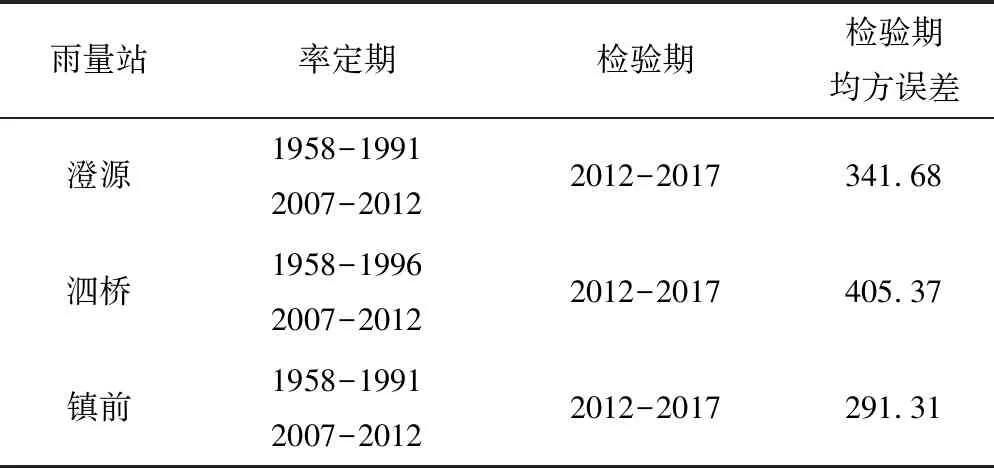
表1 率定期与检验期Tab.1 Rate of periodic and inspection period

表2 各插补站最优回归方程计算结果表Tab.2 Results of optimal regression equation of each interpolation station

表3 检验期实测年降雨量与插补降雨量对比表Tab.3 Comparison of measured annual rainfall and interpolation rainfall during the test period

按照表2所示回归方程对各个站点缺测年份的降雨量进行插补，并绘制插补后历年降雨量如图2所示，其中实线为实测降雨量系列，虚线为插补后的降雨系列。经分析可知，流域降雨资料的结果相关度较高，均方误差较小，精度较高，达到实际使用要求。对于具有短系列实测降雨、径流资料的一些流域，在进行水资源分析计算之前必须要对现有水文资料进行必要的插补，所选用的方法最好避免单一化，应尽可能实现多样化分析计算，以便达到对比分析辩证取舍的目的[8]。