HVSR法数据精细化处理中若干干扰和校正问题的解决方法研究
2021-01-26周世昌王斌战徐元璋苑益军王胜侯
周世昌,王斌战,邱 波,徐元璋,刘 磊,苑益军,王胜侯
(1.湖北省地质局 地球物理勘探大队物探所,湖北 武汉 430056;2.中国地质大学 地球物理与信息技术学院,北京 100083;3.中国地质大学 教育部构造与石油资源重点实验室,湖北 武汉 430074)
1 引 言
天然地震领域的成熟地球物理方法,通常是解决大深度,广区域的地质问题,如果将其应用到相对浅部的矿产勘探和工程勘察领域,可以解决许多能源、矿产、工程等生产问题。微动技术是利用天然产生的瑞雷面波或人工激发的瞬态瑞雷面波中不同频率成分的穿透深度和传播速度的不同,用其速度和深度(半波长)来对地下界面进行识别的地球物理勘探技术[1-6]。
基于微动的H/V法是一种更加便捷的微动方法[7-12],又称为三分谐振或HVSR方法,它最早由日本地震学家中村(Nakamura)1989年提出,它是一种估算地表层振动共振频率和放大的技术,其计算出微动信号的水平分量和垂直分量之比,典型的H/V谱比曲线具有一个明显的峰值频率fm。
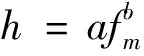
鉴于该方法划分土石分界面的应用效果良好,且布点灵活机动,故该方法在城市地质勘察中应用广泛。然而城市中震动干扰因素众多,如车辆震动干扰、高压线的电磁干扰、仪器本身的零点漂移等,均让采集的一手数据无法直接进行谱比计算,现今也少有文章全面且详细地讨论谱比计算时常见干扰因素的去除和畸变因素的校正,以及如何获得优质的谱比曲线。
本文将以武汉市江夏区法泗镇岩溶塌陷区采集的三分量地震数据为例,详细分析其中的干扰因素和畸变因素,并对如何进行去噪、校正、优质谱比曲线计算做细致介绍。
2 瞬态干扰
对采集的原始数据进行处理之前必须对原始信号进行信噪分析,从中剥离掉瞬态干扰信号。在城市道路旁采集时瞬态干扰往往源于行驶车辆和环境声音,且振幅较大,剥离瞬态干扰后余留下的有效信号才能进行频谱计算。本文标记瞬态干扰信号采用STA/LTA方法,传统的STA/LTA算法在微震监测和强震检测中用于识别突变信号(刘晗等,2014;杨黎薇等,2017)[16,20],本文用该方法识别出突变信号(突变信号在城区施工时被认为是瞬态干扰信号)STA/LTA方法的理论原理如下:
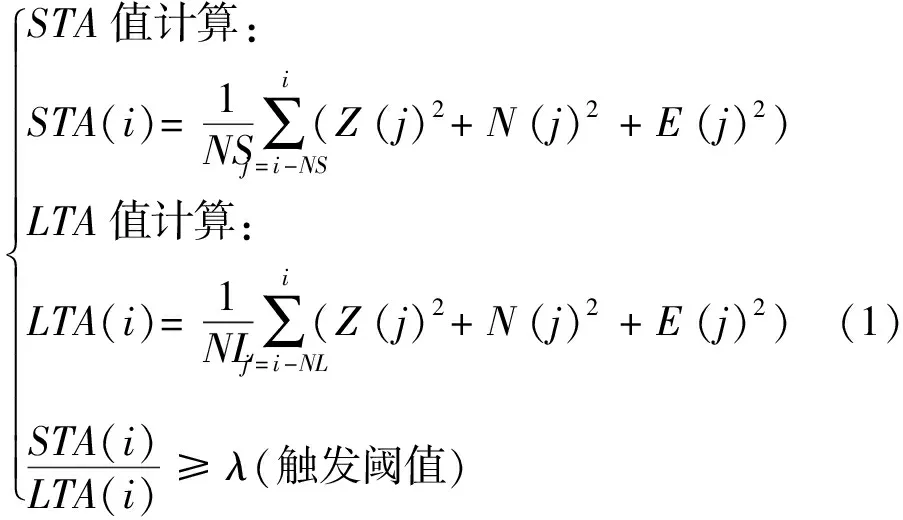
式(1)中,i为STA和LTA的计算时刻;NS的值决定了节选的信号样点数量;Z(j)为j时刻垂直分量的振幅值;N(j)为j时刻北向分量的振幅值;E(j)为j时刻东向分量的振幅值,λ为“触发阈值”。
STA值计算的样点数NS对应捕捉干扰信号的时间窗,因此时窗越短,就对短周期的干扰信号捕捉越有效,LTA值是用于衡量时间窗内的平均噪声。STA/LTA就可以根据周围环境噪声程度自适应地调整其对于某一类型干扰信号的敏感度。STA时间窗越短,越敏感,LTA时间窗越长,越敏感。对于局域干扰事件的捕捉,特别是从城市道路旁采集的数据中捕捉瞬态干扰,STA时间窗的典型值在1~10 s之间,LTA初始值一般在25 s左右,也可以适当增大。
“触发阈值”λ越小,对于干扰信号越敏感,但也容易带来误拾取;相反地,阈值越大,被识别的干扰信号就越少。通过参数试验发现,本次采集的数据STA时窗采用5 s,LTA时窗采用25 s,“触发阈值”λ选1.3,可有效识别出瞬态干扰事件(野外采集时发现这些干扰多由测线旁边高架路上的行驶车辆产生)。如图1中的“红色凸起”即为按照STA/LTA法标记的干扰事件,在预处理环节可以按照这些标识剔除掉干扰信号,保留余下的有效信号。
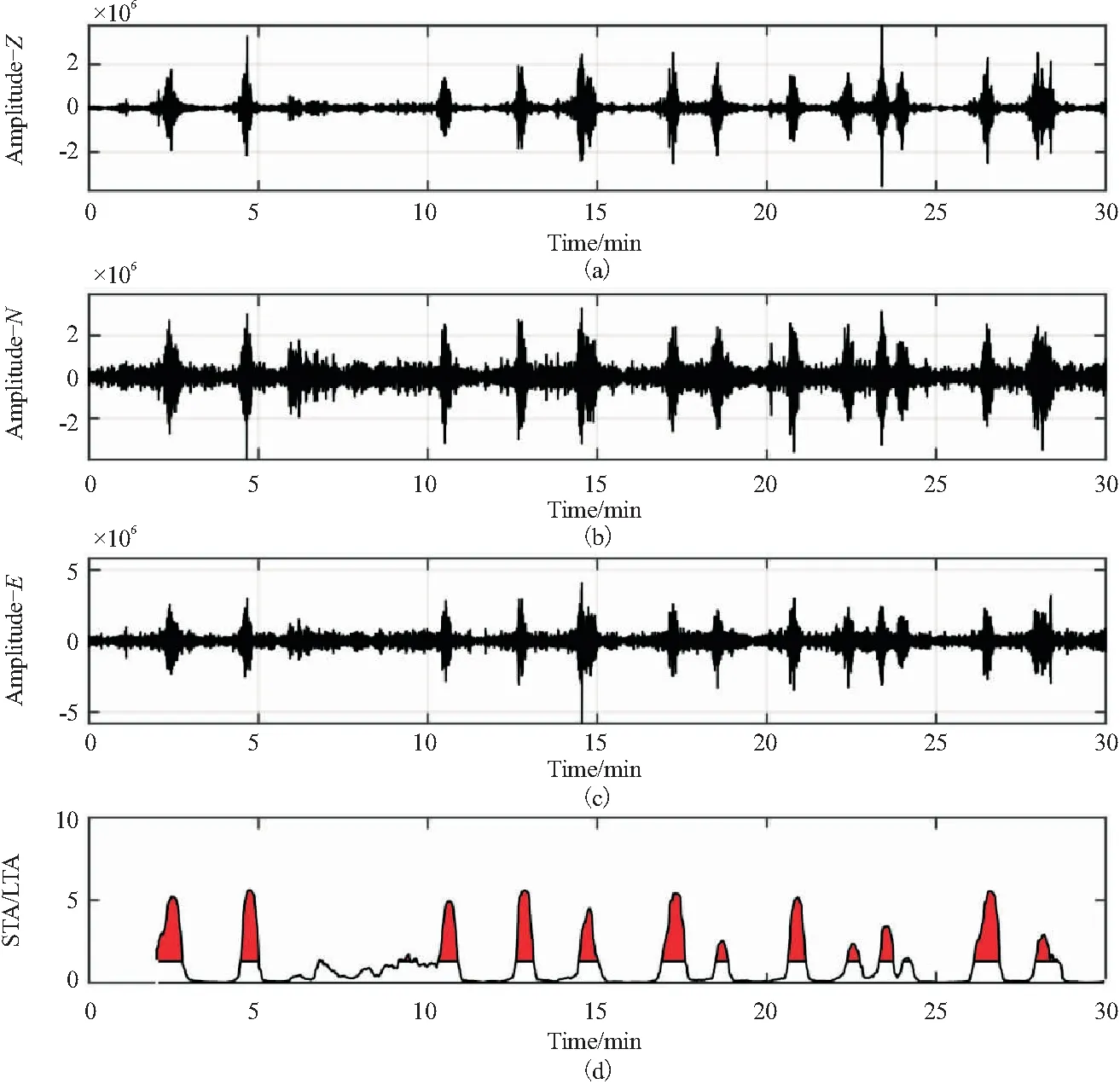
图1 采用STA/LTA方法标记出原始数据中的瞬态干扰(红色波峰)
3 零点漂移
由于仪器制造工艺等客观原因影响,现今的三分量检波器大多容易受到仪器低频噪声、环境背景信号、人为处理误差及初始加速度等的影响,由地震加速度记录积分得到的地震波位移时间曲线普遍会出现基线漂移现象(即零点漂移),造成振荡起跳点并非位于0值。如果不进行零点漂移校正,会造成低频信号的频谱值失真,从而造成低频信号的谱比值失真。
如图2所示的工区某道三分量信号,图中可以看出Z分量、N分量、E分量均存在负的零点漂移(图中绿色实线为零点基线,Z、N、E三个分量的振动曲线的中心基线均在0值往下)。用图2中信号计算频谱,结果如图3所示,频谱图中0 Hz的振幅值非常突出。原始数据中的零漂幅值可以视为一个低频分量,故造成频谱中0 Hz存在显著凸起“针状尖峰”,而有效信号幅值相对零漂幅值(即“针状尖峰”)较小,所以在频谱图中展示不够明显,故图3中2~10 Hz左右的有效信号频谱就显得尤为“矮小”。
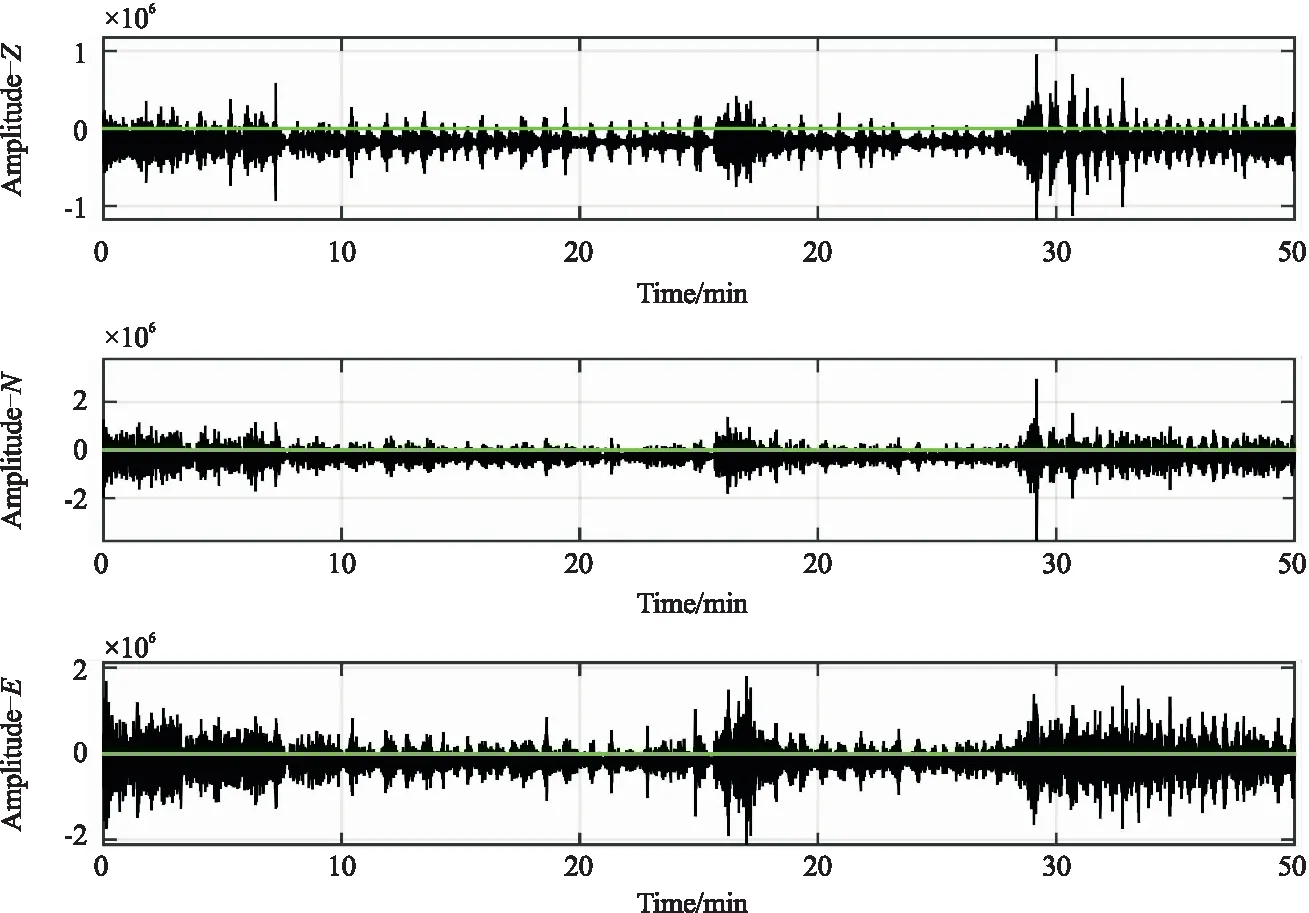
图2 原始三分量数据存在显著的零点漂移(绿线为0值线)
本文为了解决数据中存在的零点漂移,采用“分段标记重构法”,即认为在局部时间段里数据的零点漂移值为固定常数。事实上仪器的零点漂移是缓慢进行的,如果仪器零点漂移剧烈,且幅值变化较大,说明仪器本身存在故障,相应的采集数据也不可靠,必须舍弃掉。“分段标记重构法”,就是抓住零点漂移的缓慢性,通过对局部信号进行傅里叶变换获得该信号直流分量的值,并将该值用于这段信号的零点漂移校正。在实际处理步骤如下:
1)设定好零点漂移值计算时间窗长度(例如:时窗长度1 min)。
2)采用傅里叶变换计算时间窗内信号的直流分量大小。
3)按照固定步长滑动时间窗,计算下一个时间窗内的直流分量大小(例如:滑动步长为1 s)。
4)重复步骤“1)”,直到时间窗的尾部滑动到信号结尾为止。
通过如上步骤可以按照固定时间间隔对整个地震信号进行零点漂移值的估算,再对估算的零点漂移值按照信号采样率进行插值,即可获得整段信号的每个采样点的零点漂移校正值,用原始信号减去零点漂移校正值即完成了信号的零点漂移校正。图4展示了采用“分段标记重构法”对图2中数据进行零点漂移值估算的结果,图中红色实线表示估算零点漂移线,从中可以看出红色实线和振动曲线的零点漂移起伏规律十分吻合。
图5展示了图4中数据按照估算零点漂移线进行零点漂移校正的结果,校正之后数据的振动基线已经校正到0值位置。图6展示了图5中数据的频谱结果,通过图3和图6对比可以看出零点漂移校正之后0 Hz位置的凸起“针状尖峰”被去除,同时有效信号的频谱被突显出来。

图4 采用“分段标记重构法”对原始数据进行零点漂移值估算(红线为零漂线)
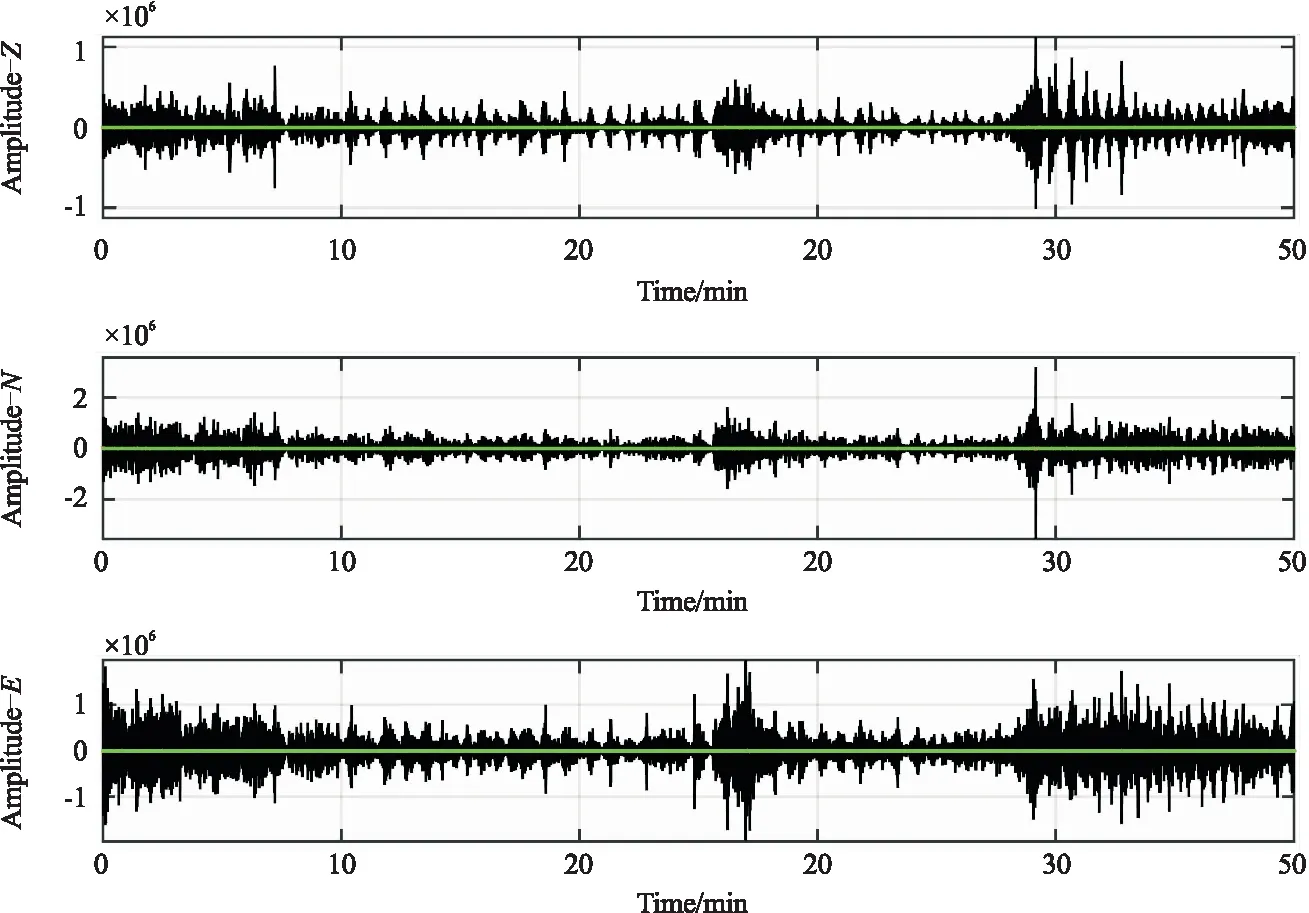
图5 进行零点漂移校正之后的数据
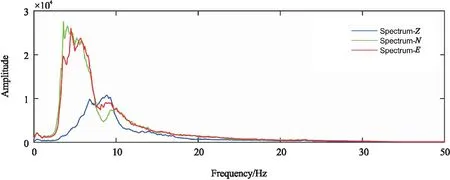
图6 进行零点漂移校正之后的频谱
4 谐波干扰
谐波干扰是原始地震数据中一种常见的干扰波,它具有振幅固定、频率单一的特点[21-25]。其主要有三个产生机制:①当检波器附近存在高压输电线时,检波器会受到工业交流电产生的50 Hz电磁场干扰,以及150 Hz和250 Hz等频率的伴随电磁场干扰。②当检波器附近存在频率固定的震源时(例如:停滞态汽车、匀速转动的马达、工作的发电机),检波器会受到单一频率的机械震动干扰。③当检波器内部漏电时,检波器也会记录下谐波电流干扰。谐波干扰一般贯穿于整个地震记录,其振幅往往明显大于有效反射信号的振幅,从而会降低地震数据的信噪比,在计算谱比值时往往在谐波干扰频率处产生畸变。因此,必须对地震数据中的谐波干扰波予以去除。
图7为数据中存在谐波干扰时的频谱图,从图中可以看到在7.5 Hz左右存在一个显著的“凸起频率”,如果不对谐波干扰进行消除会使谱比曲线的相应位置发生畸变。

图7 受谐波干扰影响的频谱
本文介绍一种“自适应谐波干扰降噪技术”来去除该干扰。在时间域,原始地震信号可以看作有效信号和谐波干扰信号的叠加,如公式(2)所示:
X=S+Y
(2)
(3)
YT=(y1,y2,…,yi,…yk)
公式(3)中XT为地震信号采样序列,ST为有效信号采样序列,YT为谐波干扰采样序列,i为采样点编号,k为总的采样点个数,T表示向量的转置。现需要在已知原始采样序列XT的情况下,估算出干扰序列YT。谐波信号用正弦函数表示如下:
yi=Lsin2πf(i+τ)Δt
(4)
式(4)中,L表示振幅;f表示频率;Δt表示采样时间间隔;τ表示初始相位参数。
(5)
由原始采样序列估算出谐波干扰序列,必须建立合理的目标函数:
(6)
其中,Q表示原始采样序列减去谐波干扰序列后的振幅能量值。随着构造的谐波干扰序列的变化,Q也会变化,而使得Q取极小值的重构序列就是实际的谐波干扰序列。将目标函数式(6)改写为向量形式如下:
要获得Q的极小值,可以对Q关于各变量求导。假设频率f和初始相位参数τ已知,对Q关于振幅L求导,并使导数为0,可以求出频率和初始相位一定时的最佳振幅,如公式(9)所示:
(9)
式(9)就是正弦函数法重构谐波干扰时的振幅计算公式,如果确定了谐波干扰的频率和初始相位,则可由该公式计算出相应的振幅值。
将式(9)代入式(7),目标函数可转化为:
式(10)和式(11)中,X是已知量,C是未知量。因此,使Q获得极小值只需要R获得极大值即可,R表达式的上方(XTC)2为原始地震序列和谐波干扰序列互相关的平方,R表达式的下方CTC为谐波干扰序列的自相关。所以,目标函数式(10)可以重新定义为原始地震序列和谐波干扰序列的归一化互相关:
(12)
使得Corr为极大值的f与τ就是重构谐波干扰的最佳频率和初始相位参数。再由式(9)计算出振幅值,根据式(4)可以重构出谐波干扰。从原始地震信号中减去重构的干扰信号进行去噪。
图8是对图7中数据采用了“自适应谐波干扰降噪技术”处理的结果,可以看出,7.5 Hz左右的“凸起频率”被消除,而其他有效频率成分的信号未有变化,即该方法在去除谐波干扰的同时,不存在伤害其它有效信号的“副作用”,在谐波干扰消除之后相应频率位置的谱比值畸变也被消除。
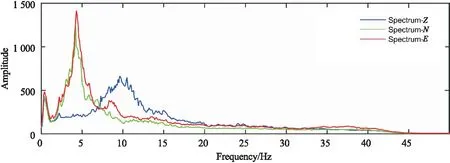
图8 采用“自适应谐波干扰降噪技术”处理后的频谱
5 谱比曲线的优化
原始数据通过有针对性的预处理后便可开始频谱和谱比计算,但是频谱计算时窗该如何选择?获得的频谱和谱比值存在‘锯齿状毛刺’该如何消除?这些问题解决不好,依然不能获得品质良好的谱比曲线。
本文采用了滑动时窗计算多个谱比曲线进行叠加来改善谱比曲线品质,在计算时采用了欧洲SESAME提出的参数确定准则(Bard and SESAME-Team,2005):
准则1 峰值频率fm和时窗长度L应该满足:fm>10/L。
准则2 时窗数量N、时窗长度L、峰值频率fm应满足:L×N×fm>200。
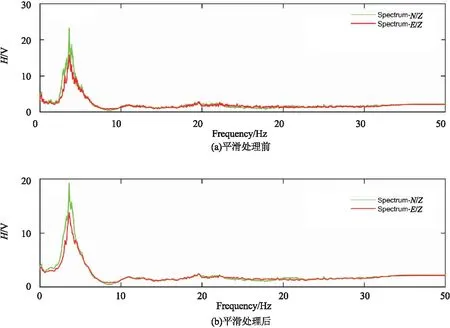
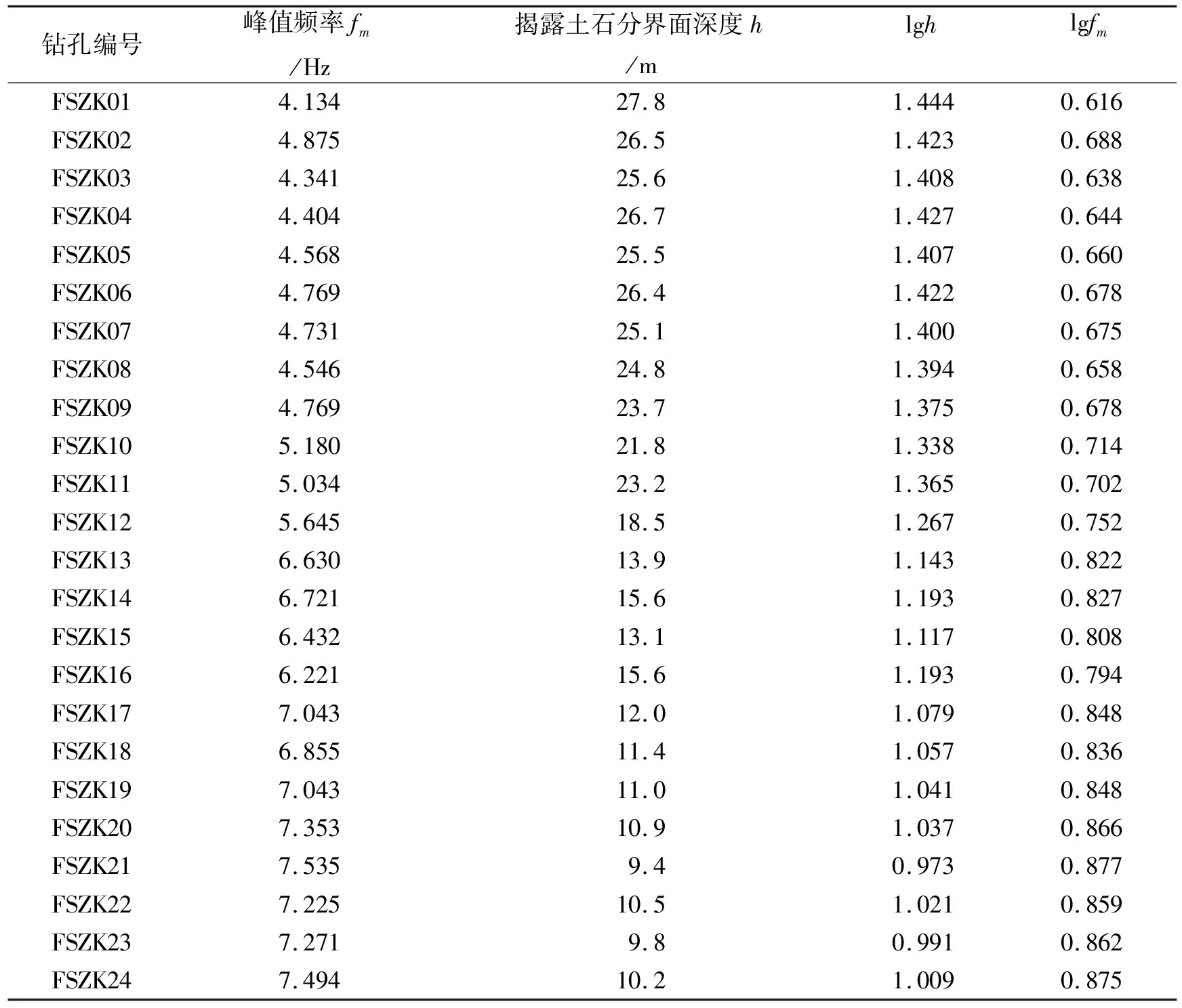
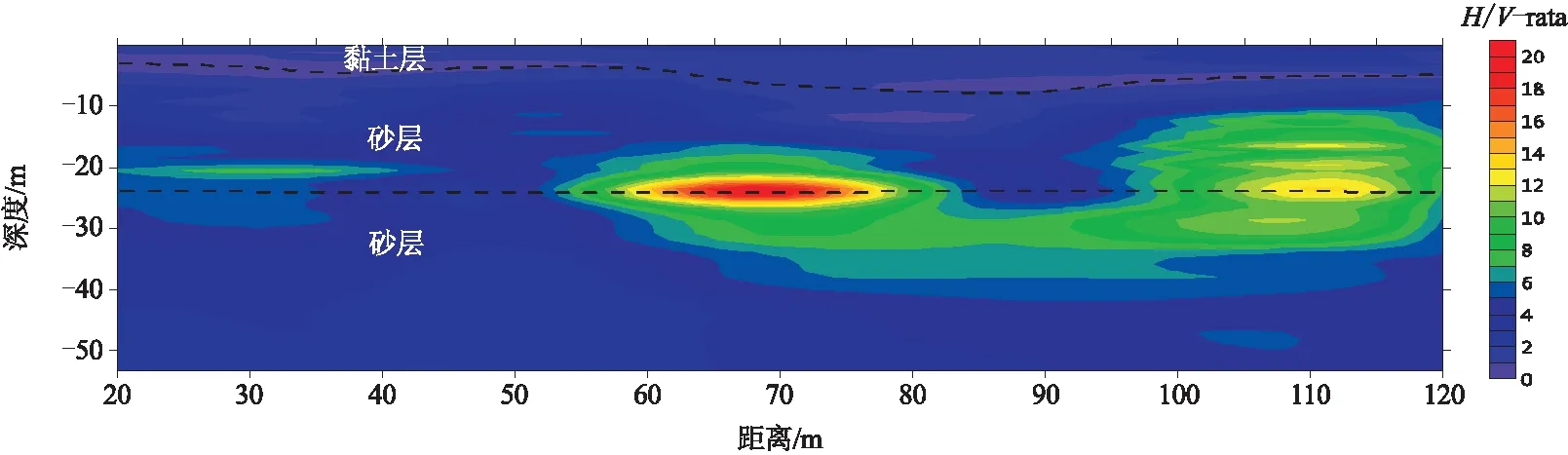
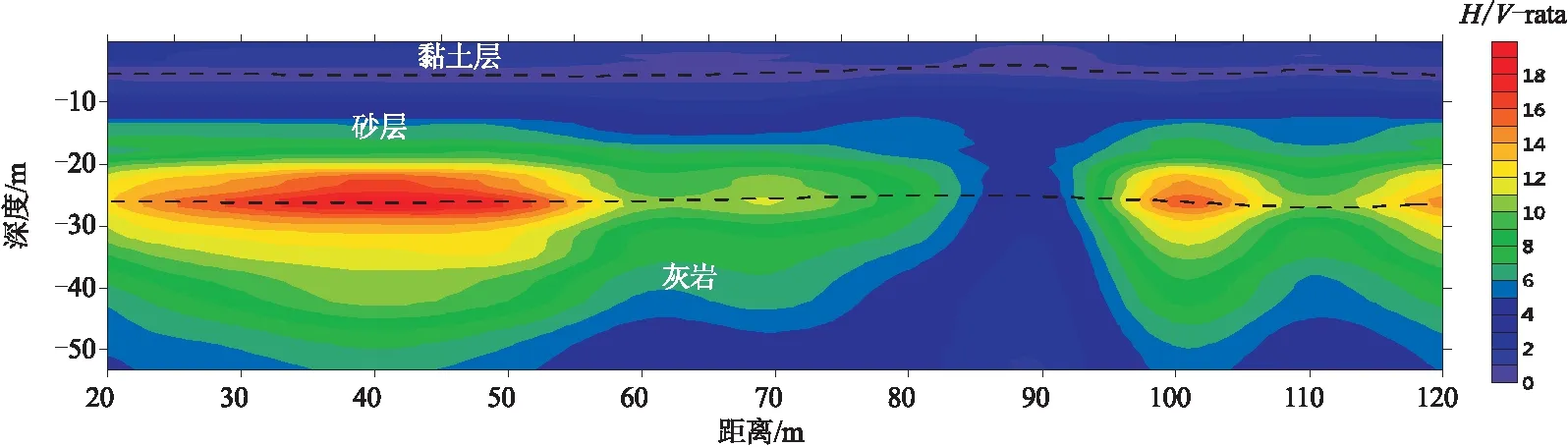
准则3 如果fm>0.5 Hz,当0.5fm 当然在数据处理的初始情况下是不知道峰值频率fm的,无法从一开始就获得较为合理的时窗长度L,实际处理时L按照一定的间隔逐步扩大,计算每一个时窗的fm值,伴随着时窗的逐步扩大,fm的值也趋于稳定,这时再选用稳定的fm值按照上述准则确定优选时窗和步长。当然也有更为简单直接的时窗选择方法(一般的三分量地震记录的总时间长度会比时窗长度L大得多),直接选用较长的时窗也可估算fm的值。 图9为工区某道三分量地震信号分别按照10 s、30 s、60 s时窗计算出的N/Z谱和E/Z谱,通过该实验可以确定在时窗长度大于10 s的情况下该道谱比曲线的峰值频率稳定在6 Hz左右,按照参数确定“准则1”可以确定本信号频谱计算时窗长度大于5/3 s即可,最终选定为10 s作为该道的处理时窗。 图9 三分量地震信号按照10 s、30 s、60 s时窗计算出谱比曲线 判断“准则3”中某个频率样点fi(0.5fm 第一步:用该频率样点fi全部时窗的谱比值计算标准差。 第二步:按照“准则3”判断标准差是否合适,如果合适进行叠加求平均。 第三步:如果“第二步”中判断标准差不合适,则舍弃掉离平均值最大的谱比值,再进入“第一步”,通过多次迭代即可获得满足要求的叠加结果。 采用滑动时窗进行叠加计算得到的谱比曲线其连续性和平滑性会显著提高,后续还可以选择性地采用帕曾窗进一步进行平滑处理(视叠加效果而定)。帕曾窗平滑处理是按照一定的频率带宽求取带宽内振幅平均值作为带宽中值频率的振幅。 图10(a)展示了工区内某道三分量数据采用单一时窗(节选了10 s长度)计算的谱比曲线,该谱比曲线存在显著的“锯齿状”特征,图10(b)是采用该时窗(10 s长度)按照1 s的滑动步长进行叠加计算,同时采用帕曾窗按照1 Hz带宽进行曲线平滑的结果,可见“锯齿状”特征得到显著改善,谱比曲线得到有效平滑。 图10 经过平滑处理前后的谱比值曲线 第四系土层和基岩分界面之间存在对应关系,土石分界面深度h和H/V谱比曲线峰值频率fm之间存在幂函数关系为(Seht and Wohlenberg,1999): (13) (14) lgh=lga+blgfm (15) 如果令:lgh=y,lgfm=x,则式(13)可表达为y=lga+bx,收集武汉市法泗地区前期开展的H/V方法获得的峰值频率和工程钻孔揭露的土石分界面深度关系如表1: 表1 武汉市法泗地区钻孔揭露土石分界面深度和H/V峰值频率对照关系 对表中lgh和lgfm进行拟合如图11所示,并对其进行直线拟合可解得b=-1.858 7(拟合直线的斜率),lga=2.641 6(拟合直线的截距),a=438.127 图11 峰值频率和深度的拟合关系 武汉法泗镇长虹村、八坛村在2014年9月5日曾发生过大规模岩溶地陷,形成了9个大小不一的锥形深坑,后用黏土和碎石对深坑进行了回填。现依托岩溶调查相关项目对塌陷回填区(塌陷坑位置已知)开展了HVSR法和其它物探方法试验。下文将展示同一塌陷部位HVSR法和高密度电法的应用效果。 图12为原始数据未进行精细化处理时获得的谱比剖面(选用全时段信号直接进行谱比计算),图13为原始数据进行精细化处理后获得的谱比剖面。两者对比发现,精细化处理前的剖面低频部分存在许多虚假异常,且谱比值的分布极不均匀,峰值频率的连续性和均一性也不好(如果不是在已知塌陷坑开展工作,仅凭该剖面判断,容易把小号40~50 m处也划定为塌陷坑),而精细化处理后的剖面土石分界面(峰值频率连线)的连续性和均一性明显提高,岩溶塌陷坑的位置和边界都更加清晰。 图12 塌陷坑回填位置的谱比法剖面(未精细化处理) 图13 塌陷坑回填位置的谱比法剖面(精细化处理后) 图14为塌陷部位高密度电法探测的结果,该方法对黏土层、砂层、基岩面分界线反映清晰,剖面中靠近大号部位的中间砂层中存在明显的一处低阻异常,该异常为原塌陷坑所在部位,与地表塌陷位置一致。 图14 塌陷坑回填位置的高密度电法剖面 通过图12和图13的横向对比说明:对HVSR方法原始数据有针对性地进行数据去噪、校正、谱比优化计算是十分必要的。通过图13和图14两种技术方法成果图的对比,以及它们和钻孔资料的对应关系可以看出,塌陷区土石分界面在HVSR法剖面上表现为低比值,在高密度电法剖面上表现为低阻。同时HVSR剖面未发现两层显著峰值,这说明HVSR法对黏土层、砂层的区分不如高密度电法清晰(此条结论仅限于本工区),但是对基岩面的响应良好(图13中卓越频率联线起伏即反映了基岩面的起伏),这也证明了该方法确实在划分土石分界面时具有优势。 1)野外采集得到的原始三分量地震数据中往往存在许多干扰和失真因素,如果采用原始数据直接进行频谱和谱比计算无法得到优质可靠的谱比剖面,需要有针对性地对其进行预处理,为谱比计算提供品质良好的振幅数据。 2)针对原始三分量数据中普遍存在的零点漂移现象和谐波干扰现象,本文采用“分段标记重构法”和“自适应谐波干扰降噪技术”可以很好地解决相应问题,为后续的频谱计算和谱比计算提供品质良好的振幅数据。 3)在频谱计算和谱比计算时为提高相应曲线的可靠性,还需从初始信号中剥离出瞬态干扰信号,而采用STA/LTA方法可以有效标记出瞬态干扰信号,按照标记可以剥离掉这部分信号。 4)为提高频谱曲线和谱比曲线的平滑性可以采用滑动时窗进行叠加(相应计算参数可遵循欧洲SESAME项目提出的准则),同时可以选用帕曾窗对单个频谱曲线和谱比曲线进行平滑处理。 5)在数据处理前需要对数据品质进行综合分析(通常从时间域和频率域两个层面进行分析),数据预处理时先进行谐波干扰去除(如果频率域分析发现存在该干扰),接着进行零点漂移校正,然后进行瞬态干扰标记与剥离,最后才能进行实质性的频谱和谱比优化计算。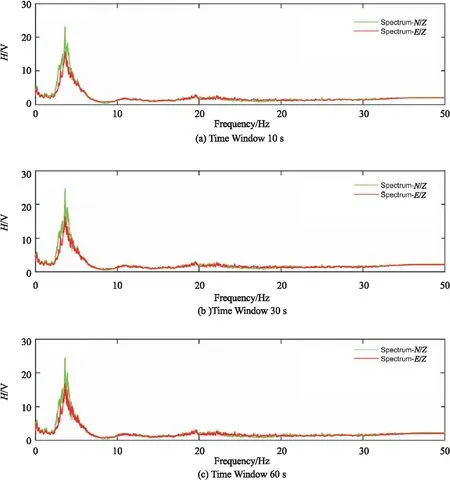
6 土石分界面和峰值频率的对应关系

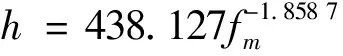
7 原始数据精细处理前后效果对比

8 结 论
