一种对抗全局窃听的网络编码方案*

周 影，褚丽莉，陈 佳

（辽宁工业大学，辽宁 锦州 121000）

0 引言

网络编码理论[1]的提出，为数据传输带来了深刻的影响，相比路由单一的存储转发功能，网络编码通过节点对上游数据进行存储—编码—转发，从而提高网络吞吐量、鲁棒性[2]和安全性。

网络编码在提升数据传输能力的同时，网络仍具有被监听的风险。针对抗窃听安全网络编码，对抗窃听攻击的方法主要有两种：信息论方法和密码学方法。Cai 等人利用传统信息论方法对抗网络编码中的窃听攻击[3]，从而使窃听攻击者窃听到网络中的任意一个窃听子集均无法通过其译码恢复出原始消息向量。在此基础上，文献[4]中进一步提出了r-安全网络编码方案，但该方案提出的前提是窃听链路数少于窃听网络链路的最大值，且不适用于多源网络。因此利用信息论实现对抗窃听的编码方案必须具备限制条件，即限定窃听者的窃听能力。

相比信息论对抗窃听攻击的局限性，基于密码学抗窃听方案更具优势。Zhang 等人[5]提出了一种P-Coding 抗窃听安全网络编码方案，该方案利用一个置换函数将全局编码系数和编码后的消息向量进行混合和重新排列，从而无法正确译码出原始数据，达到抗窃听的目的。但是需要对整个信源消息加密，并且该方案无法抵抗已知明文攻击。Fan 等人[6]利用同态加密的方法隐藏全局编码系数，从而使窃听者无法窃听信源消息，但是此方案要求在较大的有限域内进行编解码，导致计算复杂度偏高。

综上所述，本文提出一种新的抗全局窃听的安全网络编码方案，该方案不会增加宽带消耗，并且不改变中间节点的编码方式，对信源组播率没有要求。分析表明该方案可以达到安全网络编码的要求。

表1 各节点端口号以及对应端口接收的消息

1 基本模型与概念

1.1 随机线性网络编码网络模型

对于一个多元多宿网络结构G=(V,E),其中V代表网络中的节点集，E代表有向边集，节点集合包含三部分，分N={N1,N2,…,Nm}别为信源节点集合S={S1,S2,…,Sn}，中间节点集合，

信宿节点集合R={R1,R2,…,Rk}，根据网络结构，确定信源节点Si的传输速率mi，每个信源节点的传输速率决定了多播容量。信源节点Si发送m条消息至信宿节点，消息长度为n,信源消息为xi。

多源随机网络编码是不同于单源网络编码的含有多源多宿的网络结构，对于一个多源多宿网络[7]，源节点间的组播率相互约束，利用枚举法求得网络模型的可达信息率域边界C={(1,4),(2,3),(3,2),(4,1)}，为了不重复赘述两个信源的构造方法，选取区域内的的组播率都为2[8]。

1.2 窃听模型

（1）考虑多信源多信宿。

（2）窃听者可以对网络中的所有信道进行窃听，即窃听者为全局窃听者。

（3）窃听者知道网络中的整个编解码方案和消息传输方案，但无法获得加密密钥。

（4）本通信模型只考虑窃听攻击。

（5）密钥分配中心(KDC)为源节点和信宿节点分配密钥。

2 混沌系统

混沌系统是指存在于一个确定性系统中看似随机的不规则运动,其行为具有不确定性、不可重复性、不可预测性。混沌系统对初始状态和控制参数极其敏感[9]。其中，Logistic 映射属于一维混沌系统[10]，又称为虫口映射。由May 在1976 年提出，用来统计昆虫或者人口数量变化的一个简单的数学模型[11]，其表达式如（1）所示：

其中，n=1,2,3,…，参数μ表示控制参量μ∈(0,4]，变量xn∈[0,1]。

研究发现，当xn∈[0,1]，μ∈(3.569,4]时，系统处于非收敛状态，图2 为Logistic 分叉图。

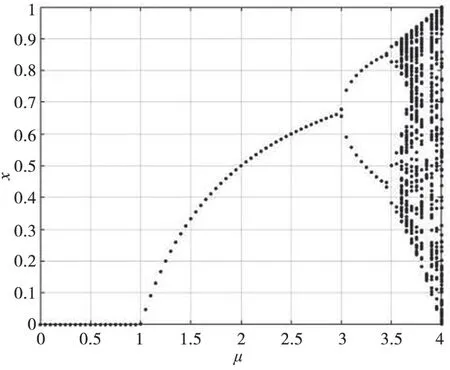
图2 Logistic 分叉图

3 编码方案

首先利用Logistic 混沌系统生成预编码系数矩阵，通过除法运算G生成所要传输的消息；将消息以随机网络编码的方式发送到下游节点；最终在信宿节点进行译码操作。编码方案流程图如图3 所示。

3.1 参数分配

混沌系统具有不可预测性，相差微小的两个初值，经过迭代后产生的数组相差甚远，且得到的结果不能计算出原始数据，根据该特性，初始值以及参数作为logistic 加密的密钥。

3.2 信源编码方案

首先，利用logistic 系统产生小数向量Y={y1,…,ym}，选取yi中的第2.4.6.8.10 位构成一个整数ti，此时ti的位范围为0 到99999，m个ti组成一个整数矩阵，形式如下：

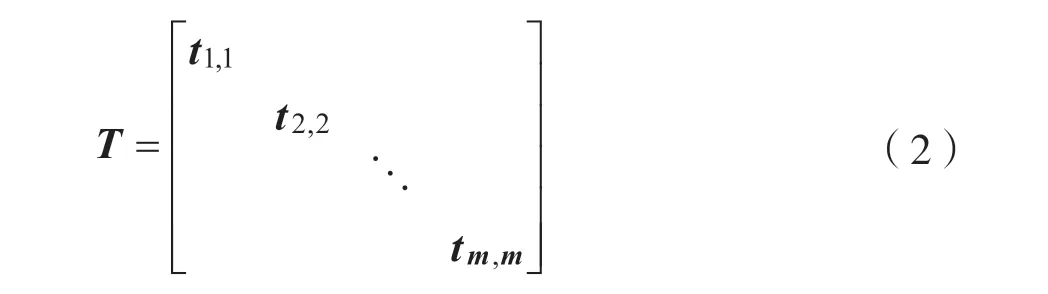
图3 编码方案流程图

通过公式（3）计算得出带有信源消息的大数非整数矩阵Z：

利用Z对信源消息进行隐藏，得到的结果矩阵为A：

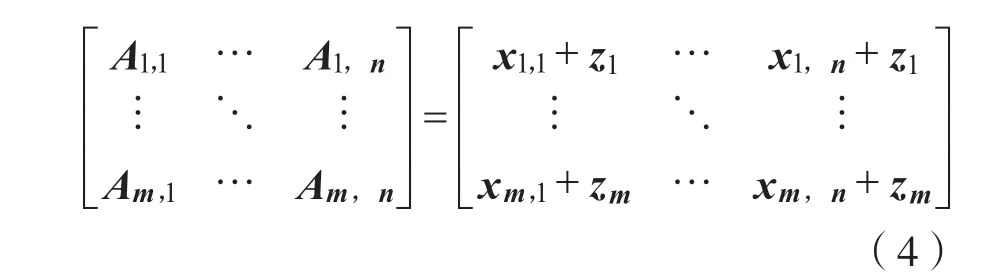
为了使消息在有限域中F28进行运算，将A变成整数，通过256 进行除法操作，得到商矩阵Qu和余数矩阵Re。通过AES 加密算法对Qu行加密成为E(Qu)，Re 序列作为被编码消息进行网络编码，最后以Data=[α|C|E(Qu)]形式传递给中间节点，其中α为系数矩阵，C为编码结果矩阵。

3.3 信宿节点解码

（1）信宿节点收到数据后，对m个非线性系数向量和结果向量进行组合，通过有限域高斯消元方法求解出余数矩阵。

（2）密钥分配中心将AES 密钥分发给各节点，解出商矩阵。

（3）通过除法逆运算求解以及logistic 解密运算解出原始数据。

4 安全性分析

结论1 攻击者在窃听全部密文的情况下，窃听者只能通过穷举法来获取信源消息。

证明：窃听者了解整个网络的编码方案，通过窃听信道获得所传输的数据Data，通过解码能得到余数矩阵Re，而商矩阵通过AES 加密进而不能够获取Z矩阵，所以只能通过穷举的方法猜测矩阵Z的数值。

结论2 窃听者通过穷举法无法获得序列Z，所以无法获得信源消息X。

证明：已知ti是由yi的2,4,6,8,10 位组成的整数，tm 属于[0，100000]，而ym 截取小数点后的12 位，范围为[10^-12，0]，z的范围在[0，10^17]。

通过计算得出t＞1，而进行网络编码信源节点的组播率m应大于1，且m，n均为整数，所以t一定大于1，能够抵抗全局窃听攻击。

5 信源编码方案举例

下面以图1 为网络模型，给出一个在有限域F28的安全网络编码（数据用十进制表示）。选取两信源节点组播率均为2，数据长度n均为1。以信源节点1 为例，x1={38,121}T。设定logistic 混沌系统初始值向量为：

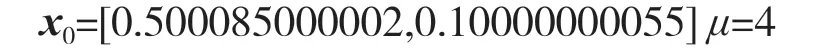
经过公式（1）500 次迭代得到y={0.8634074378729123 0.6322734168356746},利用y向量，提取T矩阵，通过公式（3）计算得到Z：

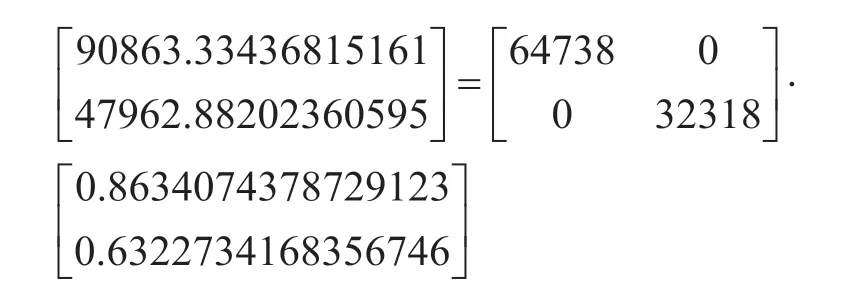
利用公式（4）计算携带信源节点1 原始消息的矩阵A：

对矩阵A进行整数运算，并对256 进行除法运算得到余数矩阵和商矩阵：

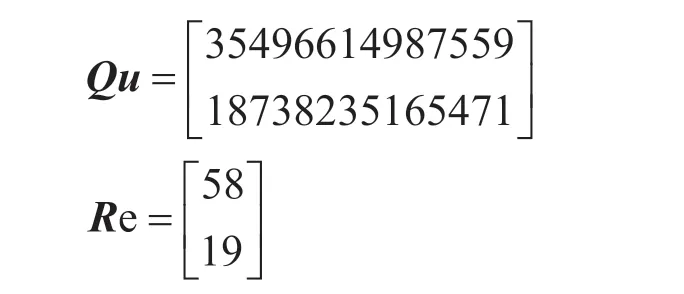
利用AES 加密算法对商矩阵进行加密，得到一维字节数组：

最后对余数矩阵进行网络编码，将系数矩阵、商矩阵加密后的字节数组以及网络编码的结果矩阵进行打包，向下传输。

6 性能分析

6.1 加密量

本文通过加密商矩阵部分防止窃听者获取明文信息，商矩阵大小为m*n，所以加密量为m*n。

6.2 通信开销

本文的编码方案不需要传输预编码矩阵，传输过程除系数矩阵和编码结果外需要添加编码冗余为m。

6.3 信源编码复杂度

在信源编码过程中，需要进行除法操作，也需要对信源消息进行网络编码，所以编码复杂度为O(m2n)。

6.4 组播率最小值

在结论二中可知，该方案对组播率没有限制，所以信源组播率最小值为1。

6.5 使用场景

经过理论验证，该方案对信源组播率没有要求，各个信源编码方案互不干涉，所以既适用于单源网络编码，也适用于多源网络编码。

7 结语

本文结合 Logistic 混沌序列提出一种抗全局窃听的编码方案，该编码方案只需在信源节点处利用混沌序列产生大数隐藏信源消息，并通过AES 加密商矩阵便可有效对抗网络窃听。相比传统方案，该方案没有增加宽带开销。本文方案只考虑窃听攻击不能抵抗拜占庭攻击，因此本文下一步研究方向为利用混沌加密对抗污染攻击。