基于迹比率的多数据集判别分析维数压缩

赵小彤， 李 智， 宋恩彬，2

(1.四川大学数学学院， 成都 610064； 2.四川大学空天科学与工程学院， 成都 610064; 3.电子信息控制重点实验室， 成都 610063)

1 引言

主成分分析算法(PCA)是数据挖掘和特征提取的有效工具，在生物信息学[1-2]、基因组学、定量金融学和信号处理等领域有广泛应用. PCA的目标是得到高维数据的低维表示，同时尽可能保留高维数据的信息[3].然而，很多实际场景通常涉及到多个数据集，其中人们感兴趣的是提取出某个数据集相对其他数据集特有的信息[1-17]. 例如，考虑两个基因表达观测数据集，它们来自于对多个种族人群的观测. 第一个数据集包含癌症患者的基因表达，是我们感兴趣的数据集，称之为目标数据. 第二个数据集则是由健康人群的基因表达组成，称为背景数据. 如果将PCA单独应用于目标数据，或目标数据与背景数据的结合，可能都仅能获得两个数据集公共的背景信息(人口模型、性别等)，而不能描述癌症患者的判别信息.为处理上述问题，Abid等[4]首次提出了对比主成分分析算法(cPCA)，并将其用于提取两个数据集之间的判别信息. 具体而言，cPCA寻找使得目标数据方差极大且背景数据方差极小的方向.cPCA在选取超参数时需要进行多次特征分解和谱聚类算法[6]，计算复杂度高. 基于文献[4]，文献[5]给出了判别主成分分析算法(dPCA)，dPCA不需要额外的超参数，计算复杂度会低一些. 但dPCA不能处理背景方差矩阵奇异的情形，且进行后续分类算法时分类效果不佳，对高维数据的低维特征提取合理性有待改进. 近期，很多学者将这两种算法应用于各种实际场景[7-8]，但这两种算法在实际应用中都具有一定的局限性.

本文提出了一种处理多数据集的新方法，称为迹比率主成分分析算法(trPCA). trPCA通过求解一个迹比率问题提取出目标数据相对背景数据特有的低维表示. trPCA能够处理背景方差阵奇异的情形，并且计算成本低于cPCA. 进一步，针对多个背景数据集情形，本文将trPCA推广给出了多背景数据集迹比率主成分分析算法(MtrPCA)，该方法可以提取出某个数据集相对其他所有背景数据集特有的低维表示.

2 预备知识

(1)

文献[4]提出的cPCA方法旨在寻找子空间使得目标数据集方差尽量大且背景数据集方差尽量小. 具体而言，我们解如下问题：

s.t.UTU=Ik

(2)

当α=0时，cPCA只选择极大化目标方差的方向，从而退化为只对xi做PCA. 当α=∞时，cPCA将目标数据投影到背景数据方差阵的零空间. 因此，α的选取至关重要.在文献[4]中，cPCA先根据多个α的预选值分别进行特征分解，然后再进行谱聚类，最终输出几个α值以及相应的子空间. 但是，对于高维数据，该算法会产生很高的计算复杂度，并且选择不适当的α会导致结果有很大偏差.

基于文献[4]，文献[5]提出了dPCA方法，即求解下述比率迹(Ratio Trace)问题：

(3)

3 算法描述

3.1 迹比率主成分分析

基于上述分析，我们提出一种新方法.考虑如下的迹比率(Trace Ratio)问题，我们称之为迹比率主成分分析算法(trPCA)：

(4)

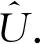
算法3.1迹比率主成分分析

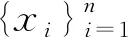
3.计算经验协方差矩阵Cxx和Cyy；

4.用二分法[10]求解问题(4)；

值得注意的是，虽然很多监督、半监督维数压缩算法最终都会转为求解迹比率问题，如线性判别分析(LDA)[13]、边界Fisher分析(MFA)[14]、局部线性嵌入(LLE)等， 但这些算法所解决的问题都与本文不同.

通过下面的定理，我们可以得出trPCA和cPCA之间的关系，证明详见文献[8].

定理3.2对d阶实对称矩阵Cxx0和Cyy≻0，U∈Rd×k，

当且仅当

由定理3.2可知，当α等于某个值时，trPCA和cPCA具有一定的等价性.

前文已经提到，dPCA的解经过任何一个非奇异矩阵变换之后还是最优解，而trPCA的解经过正交变换之后还是最优解. 因此，如果基于欧氏距离处理聚类或分类问题，trPCA的不同解得到的聚类或分类结果是不变的，但dPCA的不同解可能会使得投影后的距离发生改变，从而导致聚类或分类的结果不稳定.

注1当k=1，即提取的主成分维数为一维时，trPCA和dPCA方法是等价的，同为下述优化问题：

注2当没有背景数据时，Cyy=Id成立，trPCA退化为PCA.

3.2 背景方差奇异情形

为处理Cyy奇异情形，我们将问题(4)等价地转化为下述问题：

(5)

其中Ct=Cxx+Cyy. 问题(5)的目标函数值必然属于区间[0,1]，且最大值1对应于问题(4)的最大值∞. 我们对Cxx的零空间{x|Cxxx=0}不感兴趣，这是因为xTCxxx=0，其零空间中不包含关于目标数据集的任何有用信息，把它们从问题(5)的约束空间中移除并不会牺牲特征提取准确度. 实际上，由于属于Cxx零空间且不属于Cyy零空间的部分不可能是问题(5)的最优解，所以我们只需移除Ct的零空间.

进一步，在很多实际场景中，涉及到越来越多的高维数据，样本协方差矩阵的条件数很大，甚至接近于奇异情形. 为了更好的特征提取效果，接近Ct零空间的部分也要移除.对Ct进行特征分解可得

Ct=QΛQT

(6)

其中Λ=[λ1,λ2,…,λd],λl≥0,l=1,2,…,d.我们假设特征值已按由大到小顺序排列，Q为正交矩阵. 选取1≤d′≤d-1使得

(7)

其中阈值ε为一个很小的标量. 取矩阵Q的前d′列组成矩阵W. 解空间可以被限制在由W的列空间张成的子空间里，即U=WV,V∈Rd′×k. 从而(5)式定义的问题可以转化为如下问题，称为修正的trPCA方法：

(8)

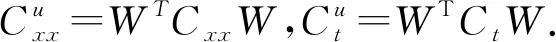
修正的trPCA算法的具体执行步骤如下.

算法3.3修正的迹比率主成分分析

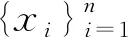
3.计算经验协方差矩阵Cxx和Cyy；

4.利用(6)式进行特征分解；

5.利用(7)去除方差阵接近零空间的部分；

6.利用二分法[10]求解问题(8)；

注4当Cyy奇异时，由问题(8)可得到和定理3.1类似的结论.

3.3 多背景数据集情形

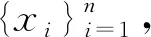
为相应的样本协方差矩阵. 我们的目标是挖掘出能明显表示目标数据，同时又不属于任何背景数据的潜在子空间向量.

基于dPCA算法，文献[5]提出了多背景数据判别主成分分析(MdPCA)，该方法求解以下问题：

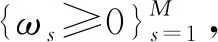
基于前面对单一背景数据的分析，我们应该寻找使得目标方差极大，且所有的背景方差极小的方向. 形式上，我们求解以下极大化问题，称为多背景数据迹比率主成分分析(MtrPCA)算法：

(9)

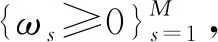
注5对于参数ωs的选取有两种方法：

(i) 用谱聚类[6]的方法选出少数几个可以产生最具代表性子空间的ωs；

(ii) 将问题(9)中的ωs与U联合进行优化.

为了验证本文所提算法在进行判别分析时的性能，本节提供了4个数值算例，与已有算法进行对比.

我们对数据集{{xi}，{yj}}应用了trPCA、dPCA与cPCA算法，其中应用trPCA算法时(7)式中的ε取成0.001， cPCA算法的参数α选为1，10和100. 单独对{xi}进行PCA算法处理. 为了便于展示，所有提取的主成分维数都为2，并且前两个主成分即为图1的横、纵坐标. 如图1所示，圆圈表示接受药物治疗的老鼠，叉号表示没有接受治疗的老鼠，trPCA可以较好地区分两个不同的子类，而PCA和dPCA算法不能很好的区分两个子类. cPCA算法对α的不同选值较为敏感，特征提取效果不稳定.

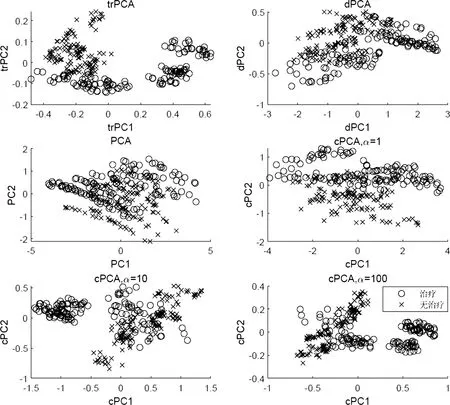
图1 寻找老鼠蛋白质表达数据中的子类

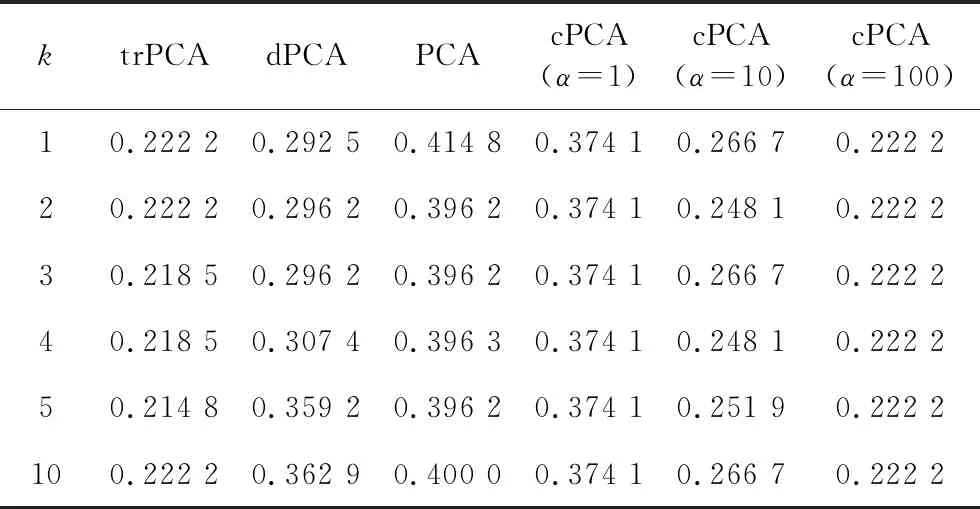
表1 基于老鼠蛋白质表达数据特征提取的聚类误差

为了进一步衡量不同算法的表现，我们先用这些算法提取出目标数据的k维主成分，再对提取后的低维表示通过K-均值聚类分成两类，最后比较这几种算法的聚类误差. 聚类误差定义为错误聚类的数据个数与目标数据的总个数的比值. 如表1所示，trPCA算法的聚类误差要小于dPCA和PCA算法，cPCA算法的聚类误差只有当选取合适的α时才会低一些，但α的选取会产生很高的计算复杂度. 因而在后面的实验中我们主要和dPCA算法进行比较.

例4.2当背景方差矩阵Cyy奇异时，dPCA算法无法处理，而trPCA算法可以通过解修正的trPCA算法来避免Cyy奇异所带来的困扰. 在第二个实验中，为了检验trPCA算法处理奇异情形的表现，我们考虑由两个目标子集构成的目标数据{xi}. 目标子类1包含120个280维向量，前200维N(0,1)，后80维来自于N(0,10). 目标子类2也包含120个280维向量，其中前200维由N(6,1)生成，后80维由N(0,10)生成. 背景数据集{yj}包含240个280维向量，前200维来自于N(0,3)，后80维来自于N(0,10)，详见表2. 此时Cyy显然是不可逆的.

表2 背景方差奇异情形下的数据生成分布假设汇总

图2 背景方差奇异时的特征提取

求解问题(8)，提取前两个主成分trPC1和trPC2可以得到如图2的结果，其中的圆圈表示子类1的数据，叉号表示子类2的数据.由图可见，trPCA算法可以很好的处理背景方差奇异的情形，并且能有效提取出目标子类相对背景数据的判别信息. dPCA算法则无法处理此类问题.

我们对数据集{{xi}，{yj}}应用了trPCA算法和dPCA算法，并单独对{xi}应用PCA算法. 提取的主成分维数为2. 如图3所示，点表示数字1，叉号表示数字2，trPCA的判别效果要优于其它两种算法.

图3 单背景叠加手写数字1和2的特征提取

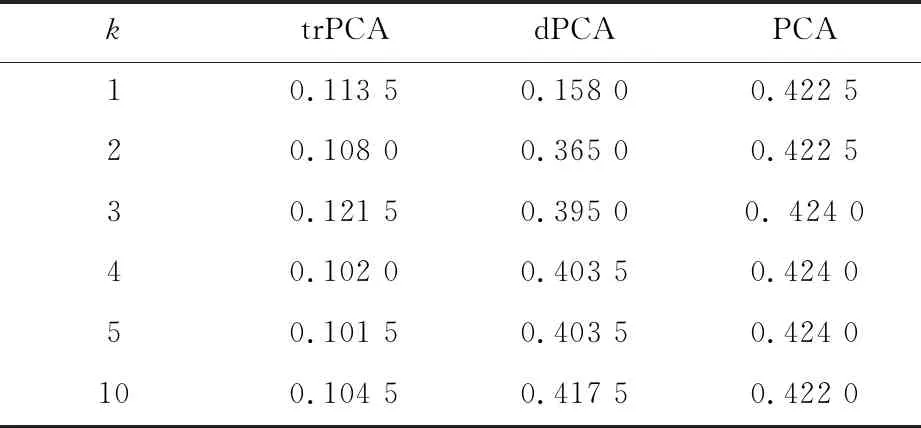
表3 基于单背景叠加手写数字特征提取的聚类误差

接下来，在提取出目标数据的k维表示后，我们进行K-均值聚类，表3给出这几种算法的聚类误差.可见trPCA算法的聚类效果远好于其它两种算法.

为了展示trPCA算法在处理高维数据时的高效性，下表给出了这几种算法在MATLAB中处理上述问题时k从1取到10的运行总时间.可见trPCA算法的运行时间小于其它算法，体现了trPCA算法相对于其它几种算法的高效性.

表4 几种算法的运行时间比较

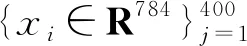
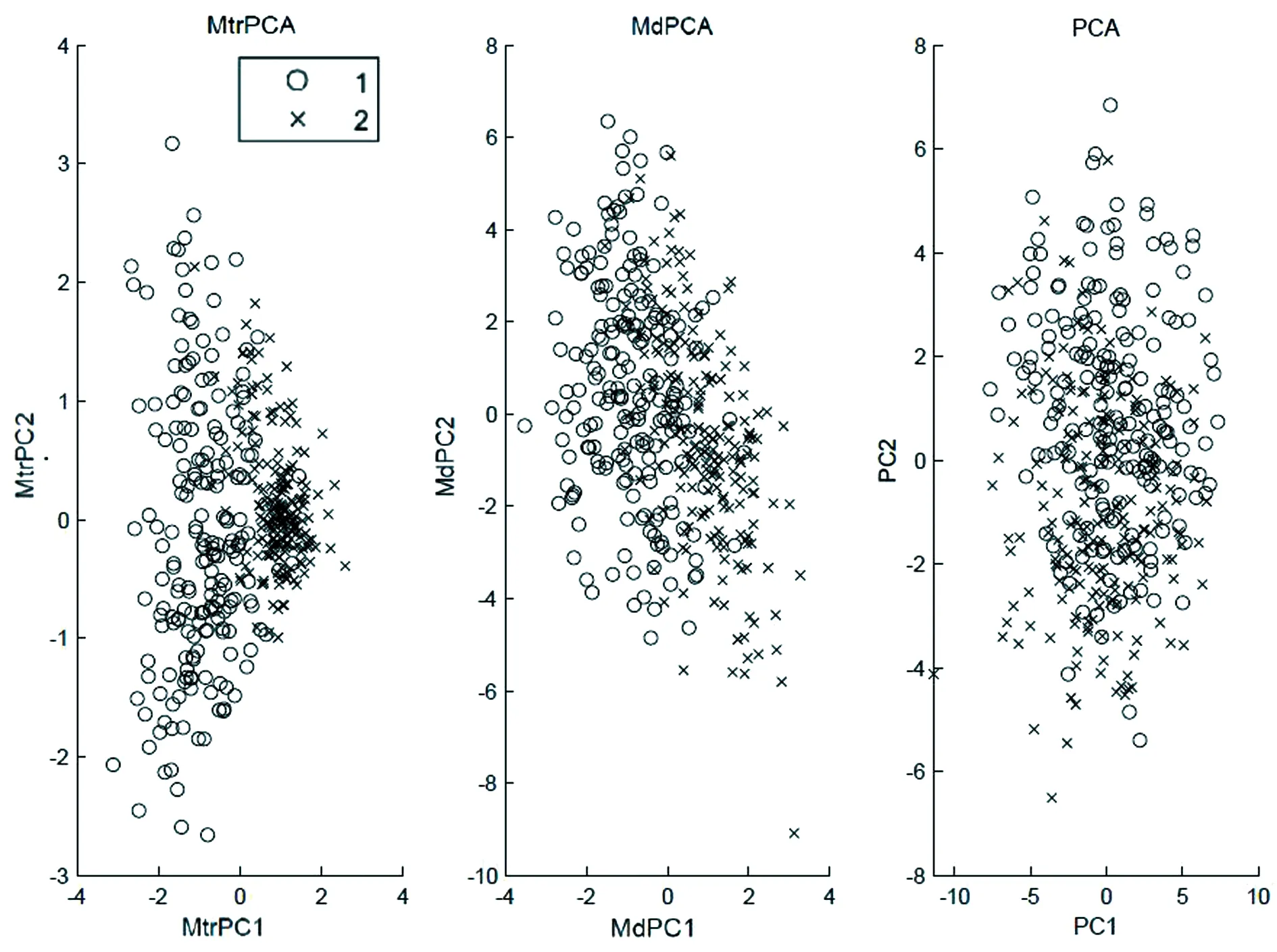
图4 多背景叠加手写数字1和2的特征提取

接下来进行K-均值聚类，当提取的特征维数不同时，相应的聚类误差如下表所示. 可以看到MtrPCA算法的聚类误差远小于MdPCA算法和PCA算法.

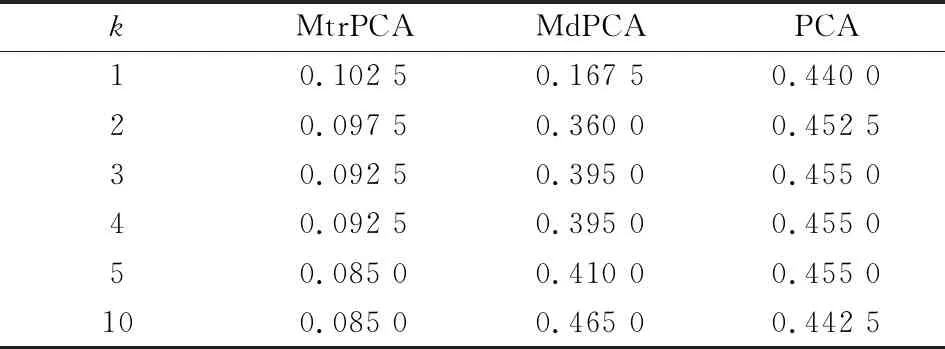
表5 基于多背景叠加手写数字数据特征提取的聚类误差

5 结 论

在各种实际场景中，我们更希望能找出某个数据集相对于其它数据集所具有的独特判别信息. 本文提出了一种新方法，称为trPCA算法，对多个数据集进行判别分析.该算法可推广至多背景数据模型MtrPCA算法. 与dPCA算法相比，trPCA算法可以处理背景方差矩阵奇异的情形，特征提取效果以及后续处理分类或聚类问题也都优于dPCA算法. 作为cPCA算法的改进，trPCA算法不需要额外的超参数且有高效的算法进行求解，计算复杂度低. 最后，多个数值模拟表明本文所提算法相较于已有算法具有更好的性能.