两相物质介电频散特性影响因素

张智韬，陈延军,2，李晓强，仵 杰,2

(1.西安石油大学 电子工程学院，陕西 西安 710065； 2.陕西省光电传感测井重点实验室，陕西 西安 710065； 3.中国石油集团测井有限公司 吐哈分公司，新疆 鄯善 838200)

引 言

岩石物理是地球物理勘探认识油气藏的基础，是衔接油气藏地质认识与油气开发的重要桥梁，以岩石物理为基础的测井是发现、评估油气藏量及产量的重要手段。岩石的介电常数是储层岩石的主要电学参数之一，是评估储层岩石里油水层分布的重要因素。在电法测井领域，利用数字岩心及数值模拟的方法对岩石介电特性进行研究成为新的热点。由于人们对储层岩石物理性质和电特性的认识不完全，在油气储层的研究与准确评估方面存在较大困难，因此在岩石物理领域开展相关实验研究工作十分重要[1]。

Francesco de Paulis等利用麦克斯韦-加内特(MG)混合公式，研究了不同频率特性组合下含有随机球形夹杂物的两相材料的等效介电常数，但内含物形态只限制为球形[2]；Pan Baozhi等计算了混合流体岩石介电特性的CRI模型和Maxwell-Garnett模型，分析了岩石介电常数与矿化度、饱和度、频率的关系，研究中并没有对内含物形态进行具体分析[3]。董航等利用三维有限差分方法分别对层状页岩模型、含极薄层结构页岩模型以及含椭球形裂缝结构页岩模型的等效电参数进行了分析，总结了频散下电特性的影响因素和变化规律，该方法缺少实际岩心结构对等效介电常数的影响分析[4]。卢静生等建立含水岩心的介电常数测量系统，通过测量在10～40 MHz下材料介电的频散特性，得到了介电常数总趋势是随频率增高而减小的规律，但测量频带过窄[5]。

本文对两相物质进行研究，弥补了复杂两相物质介电频散特性方面研究的不足。首先将两种物质按照不同的体积比混合，利用传统的模型在固定的频率下，通过Maxwell Garnett公式，研究其电特性，得到等效介电常数，再利用Debye模型研究两相物质在频散下的介电特性[6-8]。通过数值模拟两相混合物等效介电常数，将其结果与传统模型经验公式的解进行对比，验证了数值模拟的正确性。然后从数值模拟角度研究了内含物体积占比和在内部位置改变时，对等效介电常数的影响。最后通过改变内含物的状态，在真实岩心孔隙结构下，研究内含物结构对等效介电常数的影响。

1 电学理论分析

介电常数是表征电介质电能储存的能力，当电介质受到外加电场激励时，会产生不同类型的极化现象，主要分为取向极化、分子极化、电子极化以及界面极化，这些不同的极化现象具有不同的响应时间[9-11]。为了描述极化电荷分布的影响，引入了极化率χ，此时时域本构关系为

D(r,t)=ε0(r)E(r,t)+(χ*E)(r,t)。

(1)

式中：电场强度E与D均为空间与时间的函数，极化频散特性由极化率χ(r,t)表征，(χ*E)表示时间域卷积。

(2)

与式(1)对应的频域本构关系为：

D(ω)=ε(ω)E(ω)。

(3)

其中，D(ω)、E(ω)分别为D、E的傅里叶变换。

介电常数的频散特性定义为：

(4)

由时谐形式的Maxwell方程可知：

(5)

(6)

对于两相物质等效介电特性的研究，首先运用Debye模型将单个材料介电特性扩展到宽频，即

ε=ε

(7)

式中：ε∞为电介质在光频下的相对介电常数，εs为电介质在稳态时的相对介电常数，τ为弛豫时间。

其次利用混合公式计算固定频率时混合二相物质的等效介电常数，本文选择M-G(Maxwell Garnett)混合公式：

(8)

式中：εeff为混合后总体的相对介电常数(就是等效介电常数)，εi为内含物的相对介电常数，εe为外部物质的相对介电常数，f为中间夹杂物占总体的体积比。

该混合公式仅适用于内含物为球体且占体积比小的理想两相物质；最后获得宽频范围内混合物等效介电常数的频散特性。为了研究内含物体积占比较大且外形、位置复杂时混合物等效介电频散特性的影响因素，由于此时超出混合公式的使用范围，须借助数值模拟软件COMSOL计算其等效介电常数。

2 两相混合物质等效介电频散特性影响因素

本文关于两相混合物质等效介电频散特性研究中，两相混合物质分为3种情况：A.内含物材料为白云岩，外部材料为纯水；B.内含物材料为原油，外部材料为纯水；C.某井油砂岩样Micro-CT扫描数字岩心。根据相关文献得到水的相对介电常数εe0=80；εe∞=5[12]。以上3种情况内含物均无频散特性，其介电常数与频率无关(εi0=εi∞)，具体参数见表1。

借助COMSOL有限元仿真软件，基于AC/DC物理场接口中电流模块，建立两相混合物质的电容模型。首先建立几何模型，混合物质模型尺寸为100 mm×100 mm×100 mm，设置内含物为球形，根据不同的体积比推算其半径，混合物质模型上下表面放置两块铜质平行板,尺寸为100 mm×100 mm×10 mm；其次根据表1中参数设置模型材料属性、设置边界条件，上极板施加1 V电压，下极板接地，按照从内到外、从小到大、从密到疏的原则，网格剖分几何模型；最后设定求解器，计算不同频率处的等效介电常数εeff。将计算结果与M-G混合公式比较，以验证M-G混合公式的适用范围，通过调整内含物的体积、位置、个数、排列形式及其形状等参数，研究两相混合物质等效介电常数频散特性的影响因素。

表1 各组分的电特性Tab.1 Electrical properties of each component

2.1 内含物体积对等效介电频散特性的影响

两相物材料为情况A时，内含物体积占比Vφ=0.3，其他参数不变，研究其对等效介电频散特性的影响。

图1 混合物A等效介电常数εeff频散图(Vφ=0.3)Fig.1 Dispersion diagram of equivalent permittivity εeff of mixture A(Vφ=0.3)

由图1知随着频率的不断升高，等效介电常数的实部先减小后趋于平稳。对于每种极化都有不一样的响应时间，当频率升高，响应时间慢的极化作用会降低，使得等效介电常数减小。

两相物材料为情况B时，当其他参数不改变，研究改变内含物体积占比，对等效介电频散特性的影响。内含物体积占比分别为0.15、0.20、0.30、0.40的模型得到的等效介电常数如图2所示。

由图2知，内含物体积占比增大，两相物质等效介电常数值减小。并且当内含物体积占比增大，数值解和经验公式在低频部分的等效介电常数的实部出现差异，原因是传统的经验公式忽略了内含物之间的相互作用，且不包含内含物的结构信息。在内含物体积占比大和内含物与外部材料等效介电常数相差很大的时候，传统混合定理的准确性会下降。当内含物体积占比大时，通过数值模拟得到的数值解更能体现真实值。

图2 混合物B内含物体积占比Vφ对等效介电εeff频散的影响Fig.2 Effect of volume fraction Vφof inclussions of mixture B on dispersion of its equivalent dielectric constant εeff

2.2 内含物位置对等效介电频散特性的影响

在两相物材料为情况B时，固定内含物体积占比为0.20，研究改变内含物的位置对等效介电频散特性的影响。

图3显示，内含物的位置移动对等效介电常数的影响不大。对于小体积单一球形内含物，经验公式与数值模拟结果相似。

2.3 内含物形态对等效介电频散特性的影响

在两相物材料为情况B时，固定内含物体积占比为0.15，对比分析以下3种情况下的等效介电频散特性：(1)固定内含物位置下唯一内含物；(2)固定内含物位置，内含物等体积均分为8个球；(3)将内含物不等体积分割为8个球体，位置随机分布。

图4表明，当内含物体积占比小时，增加内含物数量和不同体积随机分布的内含物对等效介电常数影响不大。原因是内含物增多后，内含物结构发生变化，会导致等效介电常数变化，但由于内含物体积占比不大(Vφ<0.40)，产生的极化现象弱，因此等效介电常数变化不大。

当两相物材料为情况B，固定内含物体积占比分别为0.20和0.40时，将内含物等间隔分成4个、8个和27个球，研究内含物形态改变对等效介电频散特性的影响(图5)。

图3 混合物B内含物位置对等效介电εeff 频散特性的影响Fig.3 Effect of position of inclusions of mixture B on dispersion of its equivalent dielectric constant εeff

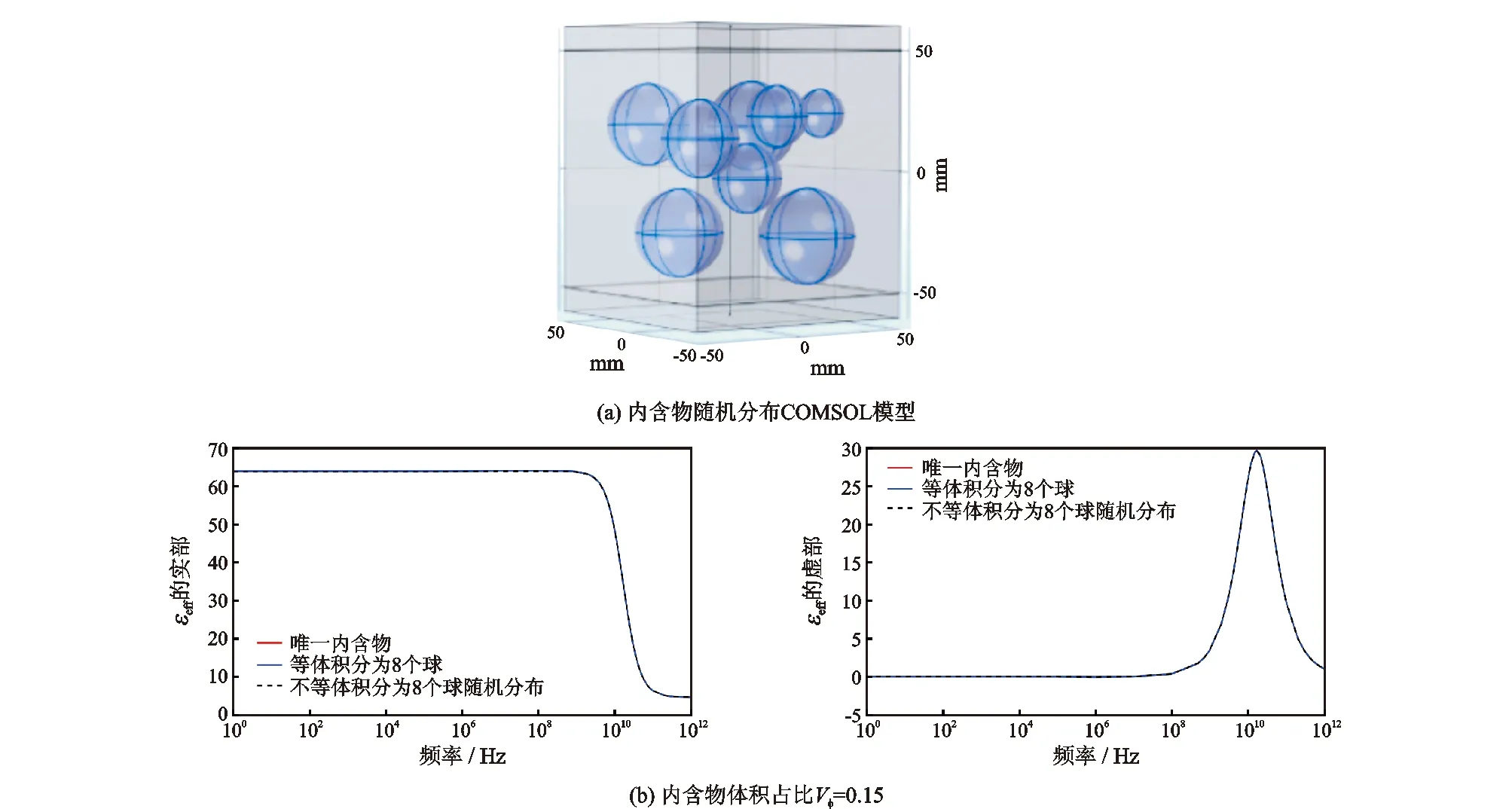
图4 混合物B小体积内含物数量对等效介电εeff频散特性的影响Fig.4 Effect of number of inclusions of small volume fraction in mixture B on dispersion of its equivalent dielectric constant εeff

由图5(b)、(c)可知，对于小体积的内含物，内含物的数量对有效介电频散特性影响不大。而对于大体积的内含物，随着内含物数量的增多，有效介电常数实部在低频下增大。原因是当固定内含物体积占比时，将内部油分成多个分散相，极化效应作用变小，对整体的等效介电常数影响变小，使得整体的等效介电常数偏向于水的等效介电常数。这种现象当内部油体积占比大的时候尤为明显，当体积占比小时影响弱。且随着内含物数量的增多，内部结构趋于复杂，界面极化现象增强，对低频部分的等效介电常数产生影响。但随着频率增大，界面极化的响应变弱，使得内含物数量对等效介电常数的影响变弱，所以高频段的等效介电常数区别不大。

两相物材料为情况B，内含物体积占比为0.40保持不变，将内部材料的形状变为圆柱体，对比分析其与球形内含物对等效介电频散特性的影响(图6)。

由图6(b)知，当内含物改变形状后对等效介电常数产生影响，等效介电常数数值变小。

对于实际岩心，本文基于MICRO-CT某井油砂岩心切片，经图像处理形成三维模型，运用COMSOL数值模拟计算该混合物等效介电常数εeff。本文岩心模型按灰度处理分为2个域，如图7(a)所示，蓝色区域材料为水，灰色区域材料为岩心填充物，分别研究岩心填充物介电常数、电导率对等效介电频散特性的影响。

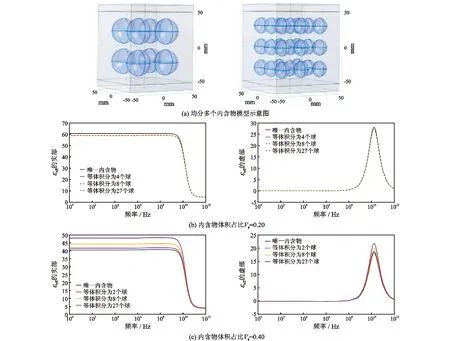
图5 混合物B大体积内含物数量对等效介电εeff频散特性的影响Fig.5 Effect of number of inclusions of large volume in mixture B on dispersion of its equivalent dielectric constant εeff

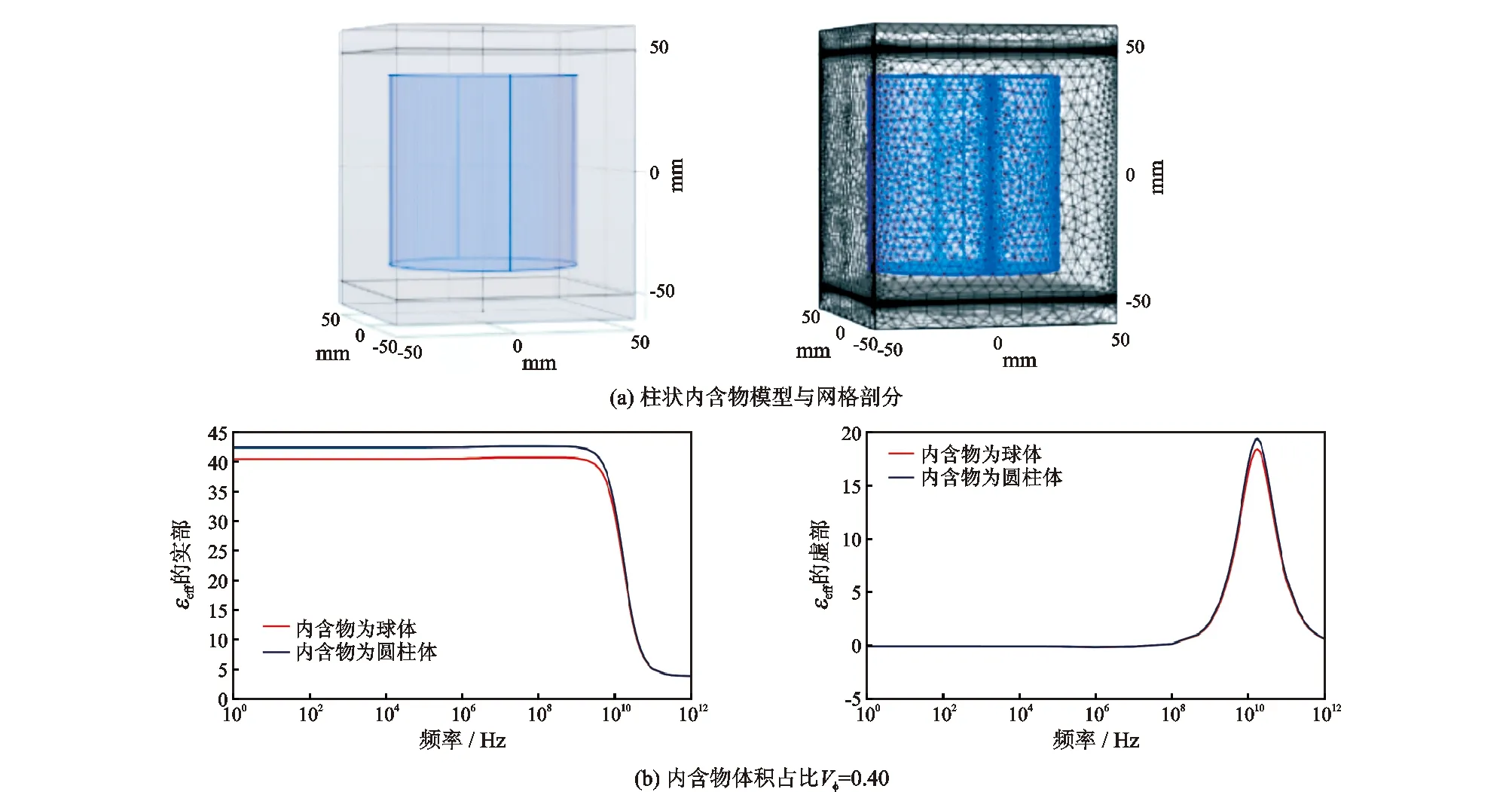
图6 混合物B内含物形状对等效介电εeff频散特性的影响Fig.6 Effect of shape of inclusions of mixture B on dispersion of its equivalent dielectric constant εeff

图7 混合物C某井油砂岩心等效介电常数εeff频散图Fig.7 Dispersion diagram of equivalent dielectric constant εeff of mixture C from oil sand core of a well

结果表明，随着内含物相对介电常数和电导率的增大，实际岩心的等效介电常数随之增大。由于实际岩心模型的孔隙结构复杂，使得εeff变化幅度增大，不能简单地用理想模型来概括。对于实际岩心，εeff实部受趋肤效应的影响，在f>106Hz时等效介电有增大趋势，在f>109Hz时开始减小。随着频率的增大，趋肤效应严重，导致等效介电常数在频率为1012Hz附近趋于平稳。而理想两相物质也存在εeff增大情形，但其增大幅度很小。

3 结 论

本文通过数值模拟研究内含物的体积大小、位置、个数、排列形式及其形状等因素对两相混合物质等效介电常数εeff的频散特性的影响。结果分析表明，当内含物体积比小于0.30时，以上有关内含物的因素对εeff的影响可以忽略不计，可通过混合公式计算等效介电常数；当体积比大于0.30时，内含物的不同形态对εeff的影响不容忽略，须通过数值模拟研究复杂形态内含物的等效介电常数特征，对于复杂孔隙结构的数字岩心模型，孔隙填充物的相对介电常数以及电导率显著影响其等效介电常数的频散特性。