黏滞阻尼墙阻尼力的理论分析及数值模拟研究
2021-01-25石文龙施佳成
石文龙 施佳成 程 荣
(1.上海大学土木工程系,上海200444;2.上海史狄尔建筑减震科技有限公司,上海200092)
0 引 言
黏滞阻尼墙的概念由日本的Mitsuo Miyazaki于1986 年首次提出,由日本住友公司最早研制成功,它是一种可安装于建筑结构上下层间的耗能减震装置[1]。钢箱体和装入其中的黏滞阻尼材料组成典型的黏滞阻尼墙,钢箱体由外钢箱和内钢板(一层或多层)构成,内钢板固定在安装楼层的上层楼面梁底,外钢箱安装在楼面梁上,外钢箱内填充了高黏度的阻尼材料[2]。在地震作用或风荷载作用下,楼层之间会发生相对位移,黏滞阻尼墙内的钢板便在钢箱中来回移动,搅动钢箱内的黏滞阻尼材料,产生剪切变形,在内钢板与外钢箱的间隙中缓慢流动。黏滞阻尼材料的变形和流动产生内部摩擦并消耗振动能量[3],从而减小结构的动力响应,达到减震的目的。由于黏滞阻尼墙可隐藏于建筑墙体内,故在实现减震功能的同时不影响建筑美观。
本文首先结合流体理论对黏滞阻尼墙能产生的黏滞阻尼力进行理论分析,定量研究黏滞阻尼力并推导出计算公式,再对阻尼墙模型的黏滞阻尼力进行ANSYS Fluent 数值模拟,得到其滞回曲线特性和阻尼力等相关信息。通过对现有缩尺黏滞阻尼墙试验模型运用这两种方法分别求解得到不同工况下对应的黏滞阻尼力值,再与试验结果进行比较来验证两种分析方法的准确性。现有黏滞阻尼墙缩尺模型试样尺寸和试验结果、数据等参考欧谨的《黏滞阻尼墙结构的减振理论分析和试验研究》第3 章相关内容[4]和周颖的《黏滞阻尼墙力学模型及其减震结构设计方法研究》[5]。
1 黏滞阻尼力的理论分析
1.1 黏滞阻尼墙的力学机制
黏滞阻尼墙的结构如图1所示[2],目前常用的力学模型是考虑了阻尼墙阻尼特性及内部刚度的麦克斯韦模型,如图2 所示[6],它由一个弹簧模型和一个油壶模型串联形成。
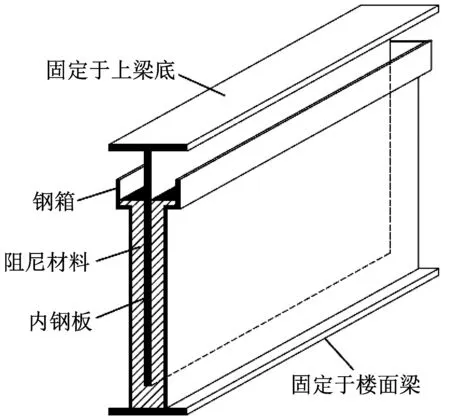
图1 黏滞阻尼墙的构造Fig.1 Construction of viscous damping

图2 黏滞阻尼墙力学模型Fig.2 Mechanical model of viscous damping wall
黏滞阻尼墙是一种速度依赖型阻尼器,其他条件不变,内钢板剪切速度越大,出力越大。目前国际上认可度较高的阻尼力计算公式主要有日本创始人提出的Miyazaki & Arima 计算公式[7]。该公式中黏滞阻尼墙的总黏滞抵抗力Qw由两部分组成:黏滞阻尼力和恢复力,所以总抵抗力公式[6]为

其中,
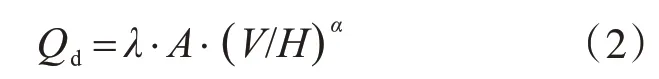
式中:Qd为黏滞阻尼力,是作用于墙体内钢板与外钢箱之间阻尼材料上的剪切力;Qk为黏弹性恢复力,是由内外钢板和黏滞材料的弹性变形产生的,使黏滞阻尼墙呈现动态刚度特性;λ 为材料黏性系数;A 为与黏滞材料接触的有效面积;V 为内外钢板相对运动速度;H 为黏滞材料的厚度;α 为由试验取得的指数,需由具体试验结果而定。
而当加载频率越低时,黏滞阻尼墙的动态刚度特性越不明显,滞回曲线的倾角也越小,此时黏弹性恢复力Qk可以忽略不计[7],因此,黏滞阻尼墙的黏滞阻尼力Qd近似等于总黏滞抵抗力Qw。故在低频加载的条件下推导的黏滞阻尼力Qd的计算公式也可用来计算总黏滞抵抗力Qw。
1.2 黏滞阻尼力计算公式推导
已有的黏滞阻尼力计算公式需要在试验结果的基础上对公式中的相关参数进行调整和确定,从而使公式计算结果与试验所得的滞回曲线拟合,而当用这些公式对其他规格和工况的黏滞阻尼墙进行计算时又会出现新的偏差或参数需重新调整的情况,故缺乏普适性。现推导一种具有普适性的黏滞阻尼力通用计算公式。
对于平行板流动,如图3 所示,由于黏滞阻尼材料是非牛顿流体,根据非牛顿幂律方程,两板间的剪切力τ为[9]

式中:μ为表观黏度;n为流变指数;γ̇为速度梯度。
根据非牛顿流体力学和流变学理论,在低剪切速率时,黏滞阻尼材料体现的非牛顿流体模型为Bingham 流体模型,而当剪切速率提高,应用Sisko 模型矫正幂律模型的无效性[10],结合一些材料的典型幂律参数,拟合曲线得到以下关系[11]:

式中:ν 表示运动黏度系数;μ 与ν 两者关系为μ=ρν,ρ为黏滞阻尼材料硅油的密度。

图3 平行板流动示意图Fig.3 Parallel plate flow diagram
再对平行板内流量进行计算[12],假设平板的长度为L,宽度为d,两板间厚度为h,且L 远大于h,d 远大于h,如图4 所示。根据y 向的平衡关系由微元法得

其中,p为压强,得到


图4 平行板内微元体示意图Fig.4 Diagram of micro-element in parallel plate
Δp 表示平行板的流体入口与出口之间的压力差,由式(6)积分可得

对于平板间层流的流体,应力及流速对于Oxy平面对称分布,所以Oxy平面处及两平板处的剪应力分别为

可得

积分非牛顿流体的本构方程得到的速度分布:

再次积分可以得通过两板间的流量:

阻尼墙计算模型样式和对应尺寸表示符号如图5所示。
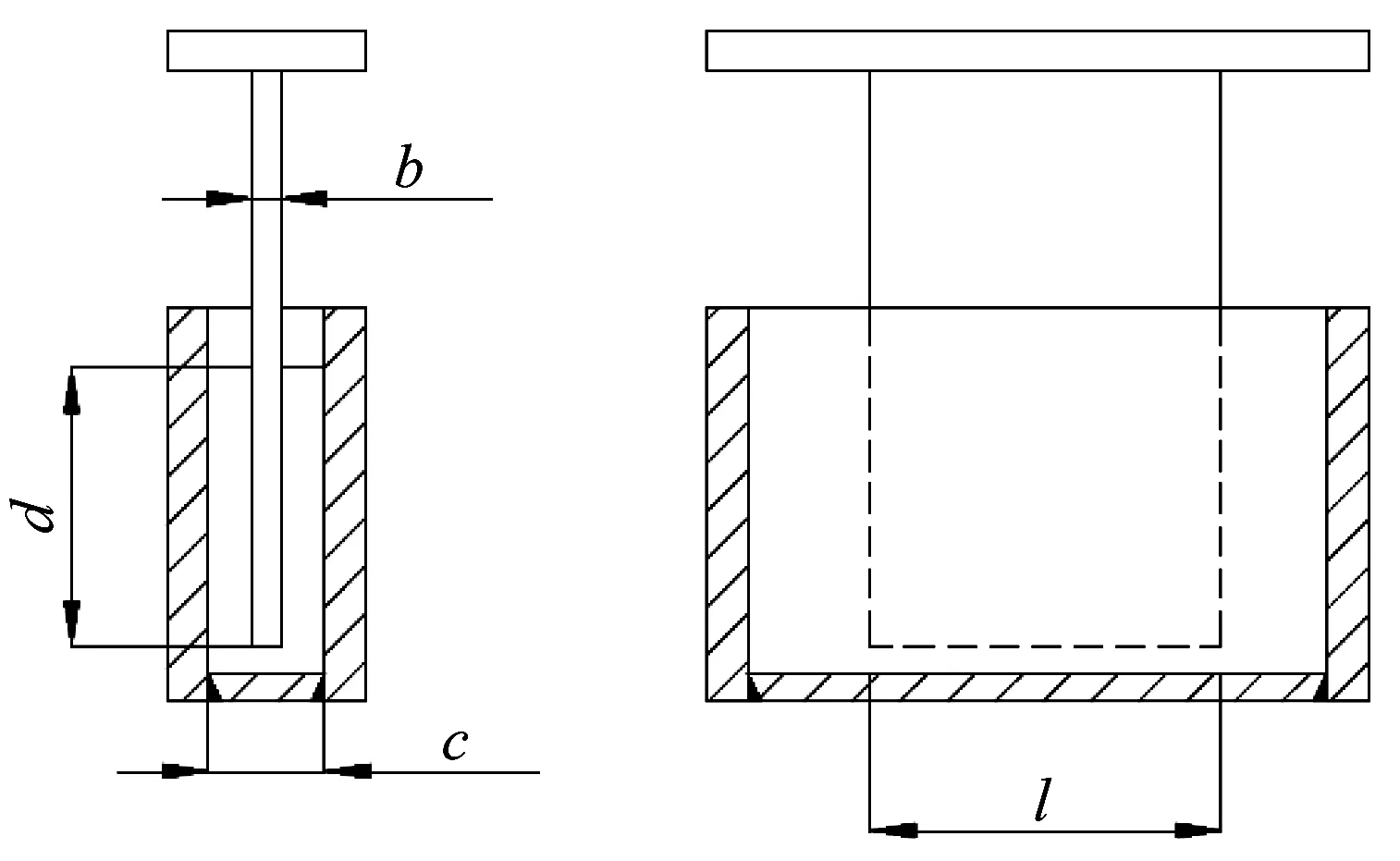
图5 阻尼墙计算模型侧视图与平视图Fig.5 Side view and flat view of damping wall calculation model
由图5 可知阻尼墙外钢箱两个摩擦面间的流量为两板间流量的2倍:

再根据图5中的尺寸关系:

可得阻尼墙钢箱容器的流量为

式中:V 为阻尼墙中钢板的移动速度;A 为摩擦面积。
又因为:

经式(12)与式(14)联立可得:
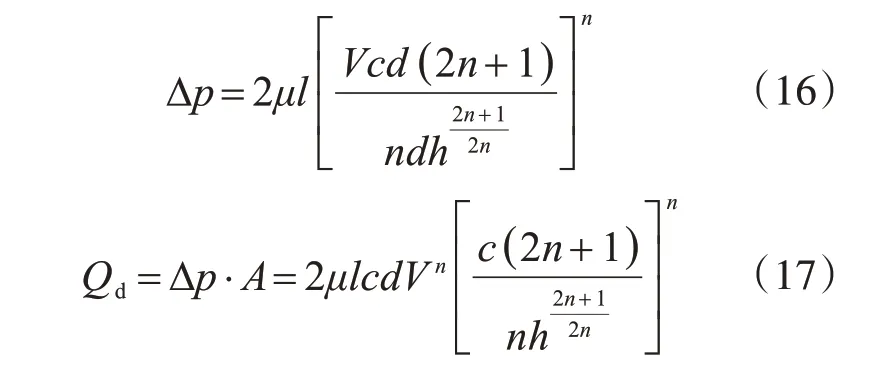
式(17)即为理论推导黏滞阻尼墙黏滞阻尼力的过程,计算特定工况下阻尼力时将对应的各个参数代入即可得到相应值。
2 黏滞阻尼力的数值模拟
2.1 背景与CFD软件概述
目前关于黏滞阻尼墙的软件模拟大多仅限于模拟阻尼墙构件在整体结构中所产生的减震效果,差异性较大,精准度不够。因此考虑通过数值模拟软件对单个阻尼墙构件进行模拟,对阻尼墙部件与黏滞阻尼材料的工作机制进行精准的建模与分析,从而得出阻尼力、滞回曲线等信息。
关于黏滞阻尼墙中阻尼材料的流动涉及计算流体动力学(简称CFD),运用CFD 法解决实际问题时,在计算机的帮助下运用区域离散化的数值计算可快速求得满足实际项目需求的解法。网格是离散的基础,目前常用的离散化方法有有限体积法、有限元法等[13]。CFD 软件专门用来进行流场的分析、计算和预测,通过CFD 软件,流场中发生的现象可以得到直观的显示,并能迅速地模拟预测所建模型的性能,通过控制微调各种数据参数,使设计效果理想化。CFD 数值模拟有助于对问题产生的原因有一个形象深刻的理解,为试验提供指导,节省试验所需的成本。ANSYS Fluent不仅提供定性结果,还为流体相互作用和平衡提供准确的定量预测和分析,它作为一款满足流体有限元模拟计算要求的软件得到了较为广泛的使用。
2.2 ANSYS Fluent建模与分析
本文选用数值模拟软件ANSYS Fluent 14.0进行黏滞阻尼墙槽道内流体压力场和速度场的模拟,最终得出黏滞阻尼墙模型内钢板所受的黏滞阻尼力Qd随时间变化的数值并绘出阻尼力滞回曲线。
首先在前处理器CFD ICEM 14.0 里建立黏滞阻尼墙二维模型如图6 所示,其中内方框代表内钢板外轮廓,外方框代表外钢箱内部轮廓,内外方框之间的区域定义为填充的黏滞阻尼材料。该模型为瞬态模型,即流场随着时间变化而变化。
再分别对内外方框和内外方框之间的黏滞阻尼材料区域划分线网格和平面三角网格,划分的局部网格样式如图7所示。

图6 黏滞阻尼墙数值模拟示意图Fig.6 Diagram of micro-element in parallel plate

图7 局部网格样式图Fig.7 Local grid map
之后将网格导入FLUENT 14.0求解器中进行材料属性和动网格参数的定义和赋值,其中黏滞阻尼材料参数的定义采用欧谨论文中试验所用黏滞阻尼材料的相关参数[4]。阻尼材料区域的属性中密度设定为970 kg∕m³,黏性选择非牛顿流体,运动黏度系数ν约为100 000 cSt,流变指数n设为0.391,动力黏度系数则由其与运动黏度系数关系转换求得97 Pa·s。对于内钢板运动属性的定义则需编写一个速度与时间的数据文档导入求解器再赋予内框边界。
2.3 数值模拟结果
后处理求解黏滞阻尼力Qd时,由于ANSYS Fluent 中没有提供以牛顿N 为量纲的监测接口,因此可以通过分析受力系数(阻力系数CD等)来求解,定义阻力系数如下:

阻力F同绕流阻力中的摩擦阻力,S是物体的投影面积,取垂直于运动速度方向的侧向面积。所以为了求黏滞阻尼力Qd,通常的方法是阻力系数CD与0.5ρV2S 相乘得到。而通过在ANSYS Fluent 求解器参考值(reference value)相应栏中将密度、速度、面积这些与阻力相关的量设为1,所监视出来的阻力系数CD值便与黏滞阻尼力值本身直接相关,因此得到各个时刻阻尼墙内钢板浸入阻尼材料单位深度对应的黏滞阻尼力Qd,再与对应深度相乘即可得到模拟出的黏滞阻尼力值,最后通过数据处理即可画出各个工况下的相应滞回曲线。
3 理论分析与数值模拟结果验证
对于黏滞阻尼墙黏滞阻尼力的理论分析和数值模拟结果还需要放到实际相应工况下与试验结果比较才能验证其准确性。
现通过参考文献[4]中的动力性能试验结果来加以验证。根据文献[4],在拟动力试验机上对黏滞阻尼墙缩尺模型进行动力性能试验,统一使用正弦激励法控制加载,位移输入按照正弦波函数曲线的样式u=u0sin(ωt)来控制加载体系对阻尼墙进行不同位移幅值,不同振动频率的加载,现选取论文中的一组试验工况进行验证。选取一组位移幅值为15 mm,温度为20 ℃,加载频率分别为0.1 Hz、0.3 Hz、0.5 Hz 的工况。以下为三种加载工况的位移x(单位:m)和速度v(单位:m∕s)计算式:

参考文献[4]中所用黏滞阻尼材料运动黏度系数ν 约为100 000 cSt,所以由式(4)可以得到n=4.5-3.55×125000.0155=0.391。再由该文献中缩尺阻尼墙模型设计图纸,可以得到图5中c、b、h、d、l对应的值分别为0.020 m、0.012 m、0.004 m、0.500 m、0.600 m。
1)工况1
该工况下通过文献[4]中原试验所得到的滞回曲线观测得出最大阻尼力约为9 kN。
由于该工况下阻尼墙内钢板最大瞬时速度V为0.003π m∕s,根据理论分析代入式(17)计算求得最大黏滞阻尼力:

此工况下通过ANSYS Fluent 数值模拟得到的滞回曲线如图8所示。

图8 工况1滞回曲线Fig.8 Hysteresis curve of working condition 1
该模拟所得位移为0 时刻最大黏滞阻尼力值为8.37 kN。
2)工况2
该工况下通过原试验所得的滞回曲线观测得出最大阻尼力约为17 kN。
由于该工况下阻尼墙内钢板最大瞬时速度V为0.009π m∕s,根据式(17)的理论分析计算求得最大黏滞阻尼力Qd≈15.49 kN。
在这种情况下,通过数值模拟得到的滞回曲线如图9所示。

图9 工况2滞回曲线Fig.9 Hysteresis curve of working condition 2
该模拟所得在位移为0 时刻最大黏滞阻尼力值为15.76 kN。
3)工况3
该工况下通过原试验所得的滞回曲线观测得出最大阻尼力约为22 kN。
由于该工况下阻尼墙内钢板最大瞬时速度V为0.015π m∕s,根据理论分析代入式(17)计算求得Qd≈18.92 kN。
此工况下数值模拟得到的滞回曲线如图10所示。

图10 工况3滞回曲线Fig.10 Hysteresis curve of working condition 3
此模拟所得最大黏滞阻尼力值为20.41 kN。
将上述案例三种工况下理论公式推导、数值模拟求得的阻尼力值与参考文献[4]中的实际试验结果整理得到表1,通过比较理论计算结果、数值模拟结果和实际试验结果得到的误差总结在表2中。

表1 案例1阻尼力值汇总Table 1 Collection of damping force values of case 1

表2 案例1计算结果误差比较Table 2 Comparison of calculation results of case 1
再用文献[5]《黏滞阻尼墙力学模型及其减震结构设计方法研究》中的试验数据结果进行验证。已知该文献中的缩尺阻尼墙模型对应图5中的c、b、h、d、l 值分别为0.014 m、0.010 m、0.002 m、0.200 m、0.200 m,结合该试验所用黏滞阻尼材料的特性,选取工况组1 和6 进行验证,两者的速度幅值为定值,分别是10 mm∕s 和60 mm∕s,同理上一个试验案例的理论公式推导和数值模拟求解验证方法进行分析,这两种工况下所得结果整理得到表3,误差分析得到表4。
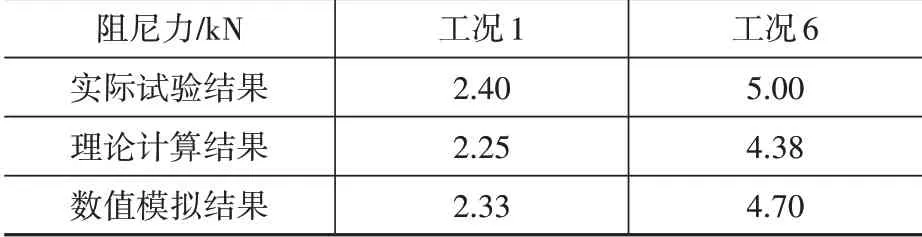
表3 案例2阻尼力值汇总Table 3 Collection of damping force values of case 2

表4 案例2计算结果误差比较Table 4 Comparison of calculation results of case 2
两个试验案例的误差分析结果充分说明了两种黏滞阻尼力计算分析方式是可靠准确的,而通过ANSYS Fluent 数值模拟得出最大黏滞阻尼力的方式相对来说精确性更高。
4 结 论
总体来说,黏滞阻尼墙的消能减震性能是比较理想的,国内外近年也出现了不少工程应用,但对黏滞阻尼墙的力学性能还缺乏系统完善的研究成果,本文通过对黏滞阻尼力的理论分析与数值模拟得到以下结论。
(1)低频加载下黏滞阻尼墙恢复力Qk可忽略不计,黏滞阻尼力Qd近似等于总抵抗力Qw,通过理论分析公式推导可定量求得不同尺寸规格不同加载工况下黏滞阻尼墙的黏滞阻尼力Qd,使公式更加具有普适性。但此理论求解的方式仍存在一定局限性,比如无法考虑温度变化对阻尼力大小的影响,高频加载下不再适用等。
(2)目前黏滞阻尼墙结构分析中的软件模拟大多仅限于模拟阻尼墙在整体结构中所产生的减震效果,无法对单个阻尼墙元件的性能进行分析。使用ANSYS Fluent 建立阻尼墙二维模型可精准便捷地对阻尼墙元件进行模拟与分析,得出阻尼力、滞回曲线等信息。
(3)通过对已有的试验,运用理论分析和数值模拟方法得出结果,并与试验真实结果比较可得出研究结果具有较为可靠的准确性,且数值模拟的精确性相对更高,在工程中也具有较好的参考意义,可将两种分析计算方法推广到实际工程应用中。
