拓扑优化在结构工程中的应用
2021-01-25高文俊吕西林
高文俊 吕西林
(1.同济大学土木工程防灾国家重点实验室,上海200092;2.同济大学结构防灾减灾工程系,上海200092)
0 引 言
为了实现结构创新以满足新的社会需求,从20世纪70年代开始,结构工程不断吸收与融合工程力学、计算机科学、材料学、机电控制、信息工程、智能技术等学科的先进技术,从而极大地丰富了自身的内涵并取得了许多创新成果。在这些跨学科技术方法中,拓扑优化(Topology Optimization)尤为引人注目。拓扑优化自诞生起经历长期发展与完善,在结构创新中逐渐显露出自身独特的优势与可持续性,促进了前沿物理、声学、光学、航空航天、机械制造、结构工程等诸多领域的技术进步与发展。在2000 年以后,随着计算机性能的大幅度提升和并行计算技术的进一步发展与普及,拓扑优化的应用范围进一步扩大:从比较简单的二维平面应力问题,推广到复杂的三维问题[1];从静力学问题,推广到动力学问题[2];从单一物理场问题,推广到多物理场耦合问题[3]。尤其是近10 年来,越来越多的工程结构借鉴了拓扑优化的结果,拓扑优化已成为工程结构创新的有力工具。主要的拓扑优化数值方法可分为基结构法[4]、均匀化方法[5]、密度法[6]以及水平集法[7]等;其中,基结构法主要用于桁架杆系结构的优化,而均匀化方法、密度法以及水平集法主要用于连续体结构的优化,详细的拓扑优化方法介绍可以参考综述文献[8]。
对于工程结构而言,拓扑优化的研究对象是结构材料在三维空间内的分布形式。无论是尺寸优化还是形状优化都需要一个给定的结构布置形式,并且这个给定的结构布置形式在优化过程中不会发生拓扑变化,既不会出现新的孔洞,也不会改变既有构件的连接方式。在传统的结构设计过程中,结构的布置形式往往依据设计人员的工程经验给出,从而具有主观性。而拓扑优化并不需要这样一个既定的结构布置,并且在优化过程中允许结构的拓扑性质不断发生变化,最终给出优化结果。
在结构理论层面,拓扑优化结果能够加深对“最优”结构形式的理解与认知。例如,Sigmund等[9]基于拓扑优化的数值结果指出:对于各向同性材料而言,类似Michell桁架(实际上,Michell桁架并不是一般意义上的桁架,而是一种非均匀各向异性连续体)的二力杆系结构并不总是最小化柔顺度问题(minimal compliance problem)的最优解;该问题的最优解在二维或者三维情况下有可能是变厚度的板壳连续体结构;而类似Michell 桁架的优化结果是由于有限元网格划分不够精细或者约束了构件的最小尺度(minimum length-scale)导致的。Aage 等[10]基于密度法对单元量级在千兆(10 亿)的机翼结构以刚度最大为目标进行拓扑优化,其优化结果表明机翼最优的结构形式由杆件、曲面肋板、连续的变厚度墙体复合而成。Sigmund 与Aage 的研究表明在边界条件和设计域较为复杂的情况下,高效的结构具有较为复杂的组成形式,并且可能包含曲面形式的连续体。
近年来,通过与具体的工程问题结合,拓扑优化在结构工程领域内涌现出许多新的应用。针对不同的工程问题,这些应用主要可以归纳为以下四个方面:①混凝土构件的配筋;②结构构件的布置;③结构构件的形态优化;④结构找形。通过拓扑优化得到的配筋布置形式能够提高混凝土构件的承载力。设计纯框架结构中支撑的布置位置以及选择超高层建筑结构中伸臂桁架所在的楼层则属于结构构件的布置问题,这类问题也可以利用拓扑优化获得合理的布置方案。而对结构构件的形态进行拓扑优化一方面可以减小构件的自重,例如,对钢梁腹板、翼缘板的开洞布置与开孔形状进行优化;另一方面也可以改善构件的力学性能,例如,通过对金属杆件的截面形式进行拓扑优化从而提高杆件的屈曲临界荷载。当拓扑优化用于结构找形时,则以结构整体为优化对象,得到指定条件下合理的结构形式。如果拓扑优化得出的结构形态较为复杂,通常还需要工程师对优化结果进行简化与归并,以便实际的施工与建造。这些应用为结构设计与建造开拓了新思路,对更加高效的结构形式进行了探索与尝试。本文将对目前拓扑优化技术在结构工程领域内的应用进行介绍。
1 拓扑优化在结构工程中的应用
1.1 钢筋混凝土构件配筋
在静力荷载作用下并且允许的体积率较低时,拓扑优化的结果往往接近纯杆件构成的桁架结构。在文献[11-12]中,这些类似桁架的拓扑优化结果被视为钢筋混凝土构件在静力作用下所形成的拉压杆模型,可以简洁地表达钢筋混凝土构件在既定荷载作用下的最优传力路径。这些研究认为,依据优化得到的拉压杆模型,在拉杆处布设受拉钢筋更为合理,但是这些研究在优化的过程中没有考虑钢筋与混凝土的材料非线性,而把整个设计域视为各向同性的弹性体。文献[11]采用渐近结构优化法,给出的算例以最小化结构总重量为优化目标,要求结构的位移需小于设置的限值;优化结果如图1 所示,图中给出了几种简单工况下的优化结果以及所对应的拉压杆模型。其中,优化结果可能带有繁杂的枝节,而实际应用中则希望配筋的布置尽可能简洁,所以拉压杆模型会根据优化结果作进一步简化。
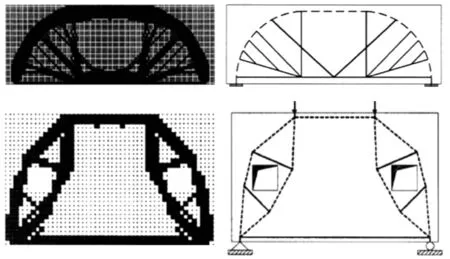
图1 拓扑优化结果与拉压杆模型[11]Fig.1 Results of topology optimization and strut-and-tie models[11]
Gaynor等[13]结合基结构法与密度法使用拓扑优化获得钢筋混凝土构件的拉压杆模型。在该研究中,混凝土与钢筋分别用实体单元和桁架单元表示;混凝土区域与钢筋部分同时进行优化;以结构整体应变能最小为优化目标,并对使用的材料用量进行限制;给出的算例如图2 所示,图中黑色区域代表混凝土形成的压杆,而红色线条则表示钢筋形成的拉杆。Yang 等[14]将Gaynor 使用的方法推广到三维的情况。Amir[15]也采用了与Gaynor类似的方法,不同之处在于混凝土本构中考虑了损伤机制。

图2 用于构建拉压杆模型的混合拓扑优化结果[13]Fig.2 Hybrid topology optimization results for generating strut-and-tie models[13]
1.2 结构构件的布置
拓扑优化能够进一步完善现有的结构体系,对原有结构体系中的结构构件布置给出更优的方案。目前,这类应用主要体现在两个方面:一方面是优化高层建筑中伸臂桁架的布设位置;另一方面是优化框架结构中支撑的布置。对于高层建筑,如果只布设一道伸臂桁架,通过穷举法可以找到最优的布置位置;但是若需要布设多道伸臂桁架,使用穷举法寻找最优布设位置的计算代价通常难以接受,而使用拓扑优化则有更高的效率。
Lee 等[16]把超高层建筑中所有可能布设伸臂桁架的位置视为设计域,如图3 所示,该设计域由离散的桁架杆件组成,每层伸臂桁架杆件的横截面积被视为设计变量,而伸臂桁架杆件的材料用量则作为约束条件,以风荷载作用下结构整体应变能最小为目标进行优化。Zhu 等[17]研究了随机激励下结构动力响应的拓扑优化问题。其中的一个算例采用了基结构法研究了伸臂桁架布置位置的优化问题,以最小化地面随机激励下结构顶层水平位移响应的方差作为优化目标,并对伸臂桁架构件的总体积设置上限,通过优化得到了布设伸臂桁架的最优楼层位置。其研究表明最优的布设位置取决于随机激励主要频率与结构自振频率之间的关系。

图3 设计域中伸臂桁架的初始布置[16]Fig.3 Initial layout of outriggers in the design domain[16]
Zhu 等[17]还对随机激励下框架结构中支撑布置的拓扑优化问题进行了研究。优化问题将最小化结构顶层水平位移响应的方差作为优化目标,并对支撑材料的总用量设置了上限,采用基结构法对支撑布置位置进行拓扑优化。为了比较随机动力优化结果与等效静力优化结果之间的区别,Zhu 等[17]对具有相同立面构形的框架,见图4(a),进行了框架刚度、支撑尺寸以及楼层质量这三方面的变化,从而获得不同的测试模型。框架刚度被分为强、中、弱三种等级;支撑尺寸被分为大、中、小三种等级;楼层质量被分为大、中、小三种等级。因此,共有27 种测试模型,对每种测试模型分别进行随机动力优化与等效静力优化。图4(b)展示了框架刚度等级为强、支撑尺寸等级为大、楼层质量等级为中的框架在随机动力优化下得到的支撑布置结果;图4(c)展示了框架刚度等级为强、支撑尺寸等级为大、楼层质量等级为大的框架在随机动力优化下得到的支撑布置结果。图4(b)与图4(c)中的框架与支撑具有相同的刚度,但是由于图4(c)中楼层质量被放大,使得结构周期延长,导致优化结果的改变。然而,图4(b)与图4(c)对应的框架在等效静力优化中获得了相同的结果,如图4(d)所示。这表明,在该情况下随机动力优化并不能被等效静力优化所取代,二者有显著区别。

图4 随机激励下框架支撑布置的拓扑优化[17]Fig.4 Topology optimization of brace placement in frames under stochastic excitation[17]
Gholizadeh 等[18]对框架结构中支撑的布置位置进行离散拓扑优化,优化目标为最小化结构的总重量,同时考虑了性能设计约束条件、构件几何尺寸约束条件以及构件强度约束条件。其中,性能设计约束条件指根据不同性能水准下的性能指标定义的约束条件,为了使得优化结果满足指定的性能要求。这些与结构性能设计相关的约束条件包括:层间位移角小于规范限值、柱构件的塑性铰转角小于规范限值以及支撑的轴向变形小于规范限值。该研究中,拓扑设计变量独立于梁、柱、支撑的几何尺寸。如图5(a)所示,对各楼层的每一跨框架可以定义两个拓扑设计变量XTi和XTj,分别对应两种可能的支撑布置位置。拓扑设计变量的值只允许取0或1;0代表该位置没有支撑,而1 代表该位置有支撑。在优化过程中,结构的抗震性能通过推覆分析(Pushover Analysis)获得。从支撑布置的优化结果可以看出,如图5(b)和图5(c)所示,各楼层支撑并没有在同一跨内从上到下连续布置,而是随楼层的不同而变化,相互之间交错排布。
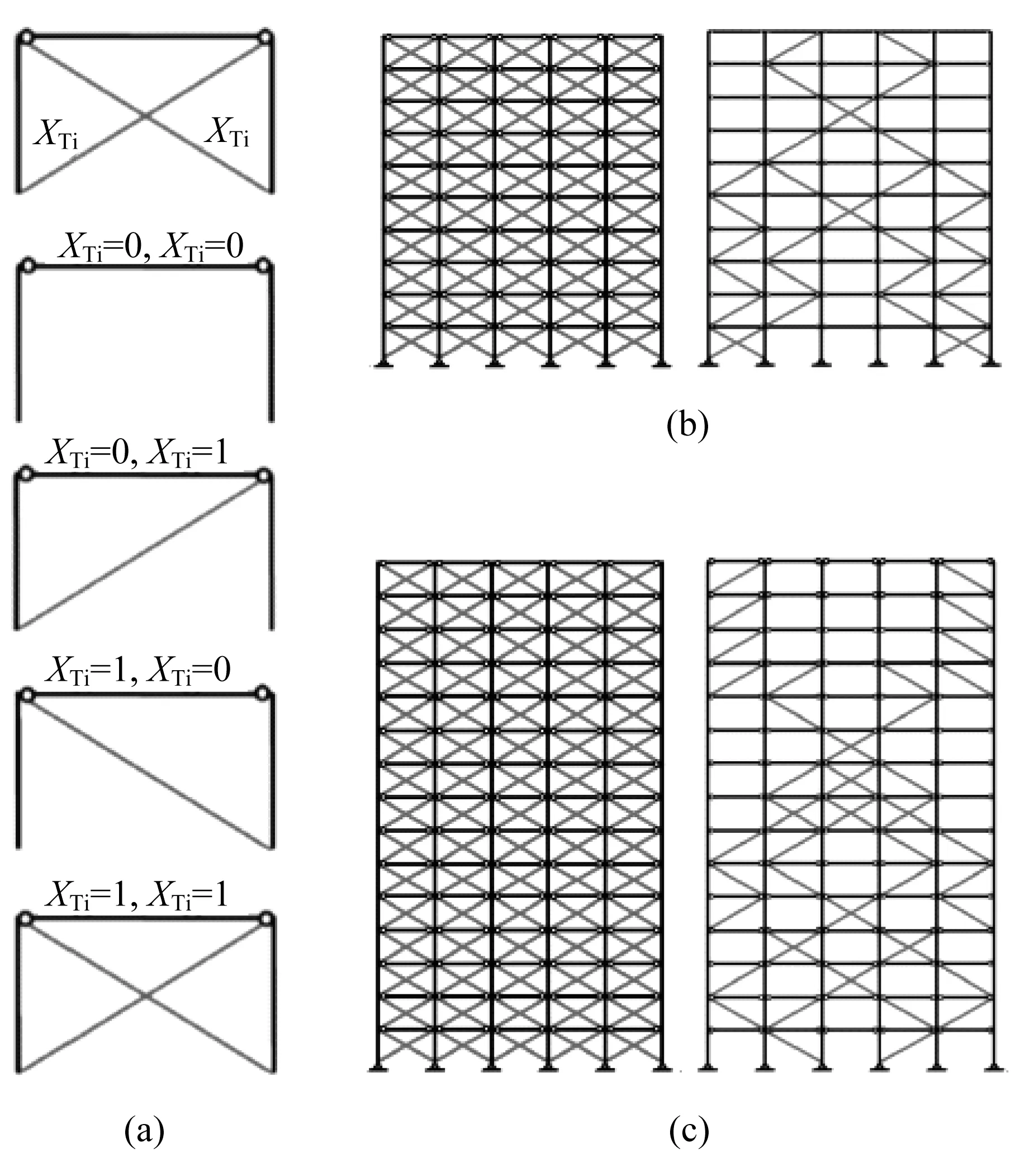
图5 框架支撑布置的拓扑优化[18]Fig.5 Topology optimization of brace placement in frames[18]
1.3 结构构件的形态优化
拓扑优化也可以用于改进结构构件的形态[19],从而使得整体结构获得更好的性能。Briseghella 等[20]将拓扑优化用于钢箱梁底部翼缘的开孔设计,为了减轻一座组合梁桥的自重,如图6 所示。拓扑优化采用了密度法,以最小化结构应变能为目标,限定了允许使用的最大材料用量。该桥因建造经费问题而一度停工,再建时却发现原设计方案难以满足新的抗震设计规范。为保留已建成的下部结构,唯有减轻桥梁上部结构的重量。经过拓扑优化后,新的设计在保证桥梁承载力与刚度的同时显著降低了上部结构的自重,从而减小了整体结构的抗侧力需求。

图6 钢箱梁底部翼缘开孔设计[20]Fig.6 Cavity design for the bottom flange of steel box girders[20]
Briseghella 等[21]还将基于密度法得到的拓扑优化结果应用于钢筋混凝土壳体的设计中,见图7。在优化过程中,通过调整壳体的材料分布,壳体受弯的区域逐渐减少,从而避免了拉应力的出现,有益于混凝土裂缝的控制;另一方面,优化后的壳体有较大面积的开孔,可以减少结构的材料用量。拓扑优化也可以结合其他优化策略与方法用于铝制梁柱构件的截面优化[22],如图8 所示,从而增加构件的刚度与稳定性。Baandrup等[23]基于密度法对悬索桥的加劲梁进行拓扑优化,优化以最小化结构应变能为目标,并限定了允许使用的最大材料用量,优化结果见图9。该研究认为,渐近分布的曲面肋板比等间距分布的平面肋板具有更高的结构效率,从而可以通过减小肋板的厚度降低结构的材料用量。但是,该研究没有考虑肋板的稳定性问题,过薄的肋板难以用于实际工程。

图7 薄壳结构的拓扑优化[21]Fig.7 Topology optimization of thin-shell structures[21]
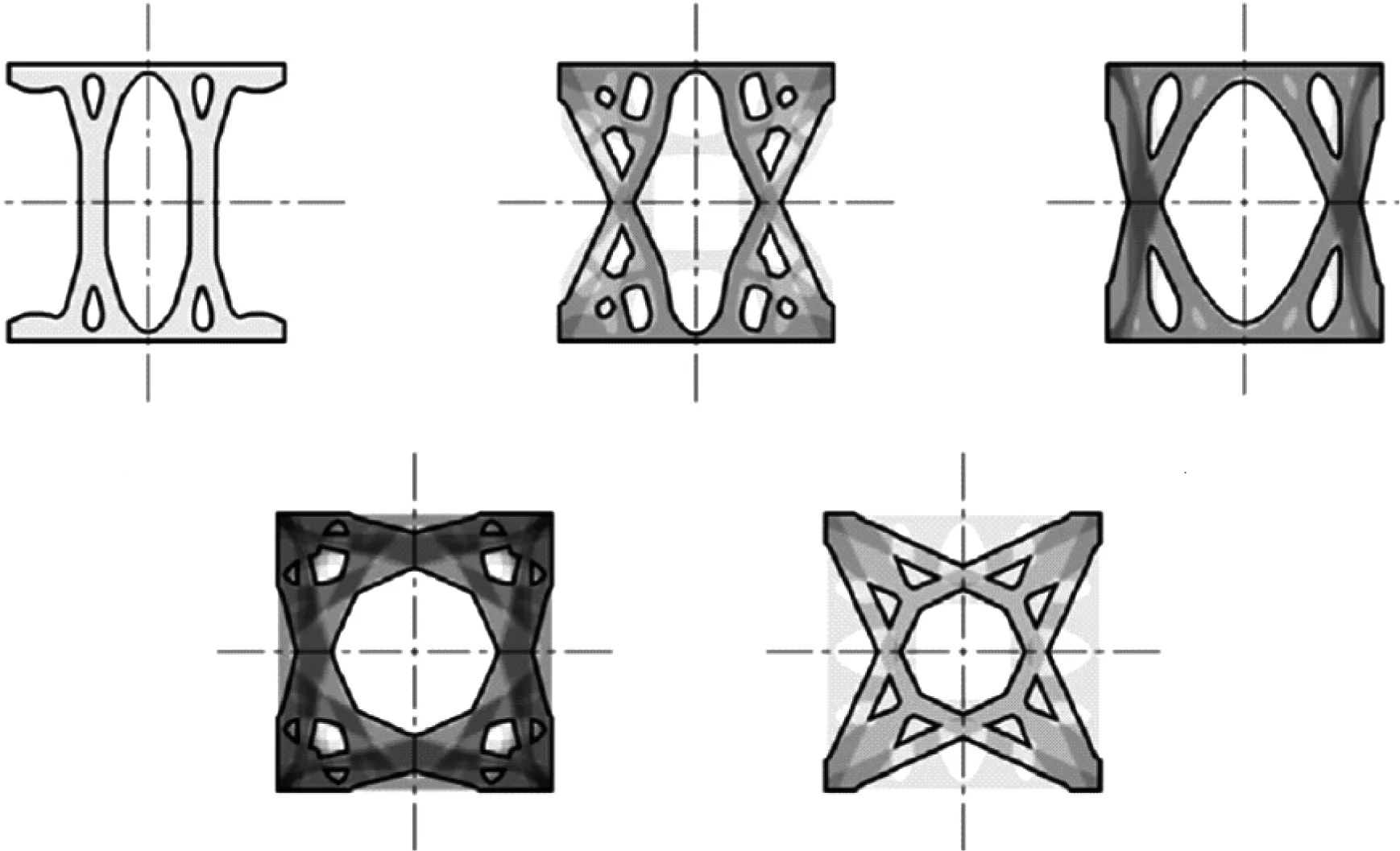
图8 柱截面优化结果[22]Fig.8 Optimization results of column cross-section profiles[22]
1.4 结构找形

图9 悬索桥大梁的拓扑优化[23]Fig.9 Optimization results of girders in suspension bridges[23]
结构找形的目的是为了找到合理高效的结构形态。在结构工程中,一个明确的结构形态需包含以下三个要素:①构件的几何外形;2)构件之间的连接关系;③构件的空间位置。尺寸优化和形状优化针对的只是构件的几何外形,通常能给出较为精细的结果。而拓扑优化则同时涵盖这三个层次,可以通过改变构件之间的连接关系与空间位置提升结构效率,从而成为结构找形的方法之一。
当设计域划分较为粗糙时,拓扑优化结果很难在构件层次上给出精细的几何外形[24-25],只能给出较为简略的结构形态,如图10(a)(b)所示。当设计域划分的精细程度提升以后,拓扑优化结果可以清晰地展示所有的结构细节,见图10(c)。对于局部结构或者结构构件的设计常使用精细的数值模型,从而获得更加细致的结构形状与几何信息。对于较为复杂的整体结构,则可以使用较为粗略的数值模型以避免难以接受的计算代价。通常使用粗略的数值模型获得的优化结果无法提供精确的几何信息,但拓扑优化结果能够给出合理高效的结构形式,为设计人员在概念设计与初步设计阶段提供有价值的参考。
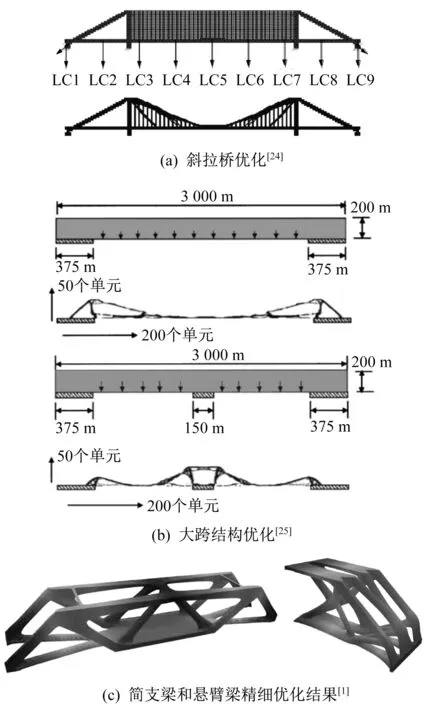
图10 不同精细度下的优化结果Fig.10 Optimization results under different resolutions
一方面拓扑优化可用于桁架结构的找形[26-27];另一方面拓扑优化也可用于框架结构体系中抗侧力系统的找形[28-30]。文献[28]采用了密度法对框架结构的抗侧力系统进行了拓扑优化。优化过程中,框架体系作为已知的结构部分内嵌于设计域中,在优化过程中不发生变化,设计域单独针对抗侧力系统;拓扑优化以最小化结构应变能为目标,限定了允许使用的最大材料用量。Allahdadian等[29]使用时域方法考虑地震激励下抗侧力系统的优化问题,采用密度法进行了拓扑优化,目标函数为自定义的结构位移范数在时域内的积分,并研究了使用持时较短的脉冲信号替代真实地震波对优化结果的影响。Qiao等[30]对具有不同抗侧力系统的框架结构进行了地震激励下的非线性时程分析,并对比了结构的损伤程度。图11(a)是Qiao 等[30]使用拓扑优化方法得到的典型框架抗侧力系统。整个抗侧力系统由相互斜交的杆件组成,每根杆件并不是直线而是曲线;此外,这些杆件的布置并不受到楼层或框架的约束,与支撑布置问题的优化结果相比更加自由。图11(b)是图11(a)简化后的结果,非线性时程分析中采用图11(b)中的结构与传统的支撑框架(见图11(c)和图11(d))进行对比。图11中圆点表示地震激励下构件的屈服位置。对比结果表明:在材料用量相同的情况下,按拓扑优化结果进行支撑布置的框架其抗震性能优于传统的支撑框架,并且依据拓扑优化结果设计的抗侧力系统能使框架受到更少的损伤。徐佳琦等[31]基于连续体拓扑优化对结构的抗侧力体系进行了研究,研究发现通过引入层间位移角限值约束后,拓扑优化结果具有明确的支撑框架形态,并且避免了不易建造的细微结构。

图11 具有不同抗侧力系统的框架在地震作用下的损伤[30]Fig.11 Seismic damage in the frames with different lateral load resisting systems[30]
超高层建筑结构抗侧力体系是决定超高层建筑结构是否经济合理的关键[32]。近年来,超高层建筑呈现主要抗侧力构件周边化、支撑化、巨型化和立体化的特点,对结构效率的要求也越来越高。文献[33-35]对于超高层建筑结构抗侧力体系进行拓扑优化,从而衍生出新的结构类型,促进了超高层建筑结构抗侧力体系的发展。Stromberg等[33]基于密度法对超高层建筑的外周结构进行拓扑优化,以结构整体应变能最小为优化目标,限制允许的最大材料用量,设计域为下方上圆的渐变筒体,优化结果如图12(a)所示,优化后的外周结构以重复渐变的斜交构件为主要特征。Stromberg等[34]的研究表明:在各区间内,巨型斜交杆件的最优相交节点在该区间3∕4 高度的位置,如图12(b)所示,并且这一结论与虚功原理的推导结果一致。文献[35-37]得到了类似的优化结果。

图12 高层建筑抗侧力系统找形Fig.12 Form finding of lateral force resisting system in tall buildings
以拓扑优化结果为主要形态特征的外周结构逐渐出现在超高层建筑的结构设计方案中[32,38-41]。文献[38-39]展示了外周结构为斜交网格的超高层建筑结构设计方案,如图13(a)(b)所示。对于高约300 m 的塔楼,抗侧力系统包括外围的斜交网格以及内部的钢筋混凝土核心筒,两者共同承担竖向力和侧向力。斜交网格形成的外周结构使得结构整体刚度较大,不需要设置环带桁架或伸臂桁架即可满足层间位移角的要求。此外,在外周结构刚度足够大的情况下,可以减小核心筒占用的面积,使内部的建筑空间更加开阔。葛文泽[40]使用PERFORM-3D 软件对图13(a)中所示具有拓扑优化结果特征的超高层结构进行了抗震性能分析,研究了该结构体系在地震作用下的塑性发展顺序,对图13(a)中所示结构是否满足实际工程要求进行了数值模拟检验,为将来可能的工程应用提供了参考信息。然而文献[38-39]中展示的外周结构,结构工程中一般称为米歇尔桁架,是斜交网格结构在侧向荷载作用下以结构刚度最大为优化目标的优化结果。但是,如果考虑水平荷载和竖向荷载组合工况,则类似米歇尔桁架的斜交网格结构不一定是超高层建筑外周结构的最优形式。因此,该问题的研究有待进一步完善。
Chung 等[41]展示的超高层建筑结构设计方案中,外周结构采用了更加简洁的形式,见图13(c)。该结构形式与Stromberg 等[34]的优化结果类似,侧向荷载经由斜交杆件传递至角柱。这些斜交杆件以轴向变形为主,具有较高的结构效率,但会导致楼面梁有轴向力。陈才华等[42]对巨型斜撑框架-核心筒超高层结构进行了模型振动台试验。试验结果表明:以斜交杆件为特征的外周结构不仅增加了整体抗侧刚度,使刚度沿竖向的分布更均匀,同时增加了整体抗扭刚度。

图13 超高层建筑抗侧力系统设计Fig.13 Designs of lateral force resisting system in super tall buildings
2 未来的研究趋势与发展方向
本文回顾了近年来拓扑优化在结构工程中的应用,涉及钢筋混凝土构件的配筋、结构构件的形态优化与布置优化以及结构整体找形等多个层面,并对当前的发展现状进行了介绍,为今后的应用与研究提供了较为丰富的参考文献。在结构工程的未来发展中,结构设计会更加精细与合理,结构形式将不断优化。其中,结构创新是历久弥新的主旋律,而拓扑优化作为结构创新的一种重要手段将为结构工程的发展注入新的活力。特别是在非传统结构设计与功能结构设计中,拓扑优化具有广阔的应用前景。其中,具有价值的应用方向包括但不限于:
(1)设计受力复杂的构件或者节点。钢结构网架的支承节点往往有多根杆件汇交,常采用半球状铸钢连接节点,而高位斜撑—柱转换支承节点常采用分叉树枝状铸钢连接节点,这类铸钢节点受力复杂设计难度高。目前,已有学者开展了探索性的研究[43],将拓扑优化应用于复杂节点的设计,以提高此类节点的整体性能。此外,拓扑优化也可以应用于索杆结构中典型节点的设计,从而获得受力合理、形式新颖且具有美感的节点形态[44]。
(2)优化需要大量重复制作的预制构件,以及需要重复建设的基础设施。由于需要重复制作或建造,减少结构的材料用量能带来巨大的经济效益。而拓扑优化是提升结构效率,减少结构材料用量的有效方法。
(3)复杂结构、超高层结构整体找形。大高宽比(大于10∶1)、倾斜体型、扭转体型、核心筒偏置等复杂形体的超高层建筑以及由超高层建筑群组成的“空中城市”将给结构设计和施工提出更大的挑战[32]。寻求高效合理的结构体系是这类高难度结构设计的关键,而使用拓扑优化能为复杂的结构设计提供合理的结构形式。
(4)提升动力作用下的结构性能。在大跨桥梁或者超高层建筑抗风问题中,结构形体与颤振、涡振等动力现象紧密相关。合理的结构形体能有效减小这些负面的振动效应,提高结构的安全性。而拓扑优化是获得合理结构形体的有效方法,通过拓扑优化减小结构的风致振动是未来的研究方向。在建筑结构抗震中,可以对结构抗侧力构件的布置或者结构的抗侧力体系进行拓扑优化,从而提升结构的抗震性能。但是,此类研究中目前多采用静力荷载或者等效静力荷载进行结构优化,没有充分考虑结构的动力特性,所以在未来的研究中还有待完善。
目前与结构拓扑优化相关的研究主要侧重结构的优化方法,已开展的研究常以优化方法的局部细节改进为创新点,注重阐明改进后的优化方法带来的变化,但缺少面向工程应用的考虑与讨论,也缺乏系统的对比分析和试验验证。系统的对比分析需包括:1)结构的线性与非线性性能分析;2)结构的鲁棒性;3)结构造价与结构的材料用量。其中,结构造价是工程实践所关心的问题,但是经常被忽略。试验验证则包含静力试验与动力试验两个方面。其中,使用振动台对新型结构进行模拟地震激励试验是研究结构抗震性能的有效方法。在试验的过程中,由于拓扑优化结果通常具有较多的复杂汇交节点,试验模型的制作与加工将会面临挑战。
目前可以实现拓扑优化的软件有Altair Solidthinking Inspire、HyperMesh、Altair OptiStruct
等,一些著名的大型商用计算分析软件(例如,AnsysAbaqusComsol 等)也添加了相应的结构拓扑优化模块,以便普通结构设计人员使用,降低了拓扑优化的应用门槛。然而,对于复杂的拓扑优化问题,商用计算软件中的内嵌模块并不能充分满足要求,也不能提供灵活的计算框架。目前,研究人员解决复杂拓扑优化问题时,仍然倾向使用面向过程的编程方式建立有限元模型并编写优化程序。这需要具备相关的编程经验以及数值计算方面的专业知识与技巧。因此,拓扑优化在复杂问题中的应用往往需要经验丰富的研究人员参与。在未来,拓扑优化技术将进一步发展,并且与结构工程的联系会更加紧密,相关的技术应用值得结构工程领域研究人员关注与学习。
